系统配置dns主从服务器
一、准备两台主机,区分主从
![]()
二、完全区域传送
1、主DNS服务器配置
#安装相关的包
[root@oula1 ~]# yum install bind -y#关闭防火墙
[root@oula1 ~]# systemctl stop firewalld
[root@oula1 ~]# setenforce 0#修改配置主文件
[root@oula1 ~]# vim /etc/named.conf
options {listen-on port 53 { 192.168.75.129; };#定义监听端口,如果所有地址都监听,则只写端口directory "/var/named";#定义数据文件目录allow-query { any; };#允许所有主机进行查询recursion yes;#开启递归查询allow-transfer { 192.168.75.129; };#从服务器ip
};
#正向解析模块
zone "baidu.com" IN {type master;file "master.baidu.zheng";
};
#反向解析模块
zone "75.168.192.in-addr.arpa" IN {type master;file "master.baidu.fan";
};#编写资源记录文件
#1、正向解析
[root@oula1 ~]# vim /var/named/master.baidu.zheng
$TTL 1D
@ IN SOA @ admin.baidu.com. (01M1M3M1M )NS dns.baidu.com.NS slave.baidu.com.
dns A 192.168.75.129
www A 192.168.75.130
ftp A 192.168.75.132
slave A 192.168.75.131
w CNAME www
#2、反向解析
[root@oula1 ~]# vim /var/named/master.baidu.fan
$TTL 1D
@ IN SOA @ admin.baidu.com. (01M1M3M1M )NS dns.baidu.com.NS slave.baidu.com.
129 PTR dns.baidu.com.
130 PTR www.baidu.com.
133 PTR w.baidu.com.
132 PTR ftp.baidu.com.
131 PTR slave.baidu.com.#重启服务
[root@oula1 ~]# systemctl restart named2、从DNS服务器配置
#安装相关的包
[root@oula2 ~]# yum install bind -y#关闭防火墙
[root@oula2 ~]# systemctl stop firewalld
[root@oula2 ~]# setenforce 0#修改配置主文件
[root@oula2 ~]# vim /etc/named.conf
options {listen-on port 53 { 192.168.75.131; };directory "/var/named/slaves";allow-query { any; };
};
zone "baidu.com" IN {type slave;file "slaves.baidu.zheng";masters { 192.168.75.129; };allow-notify { 192.168.75.129; };
};
zone "75.168.192.in-addr.arpa" IN {type slave;file "slaves.baidu.fan";masters { 192.168.75.129; };allow-notify { 192.168.75.129; };
};#重启服务
[root@oula2 ~]# systemctl restart named三、增量区域传送
1、主DNS服务器配置
#在二配置的基础上,如资源记录文件有变(#号标记处),需编辑正反向解析资源记录文件
#1、正向解析
[root@oula1 ~]# vim /var/named/master.baidu.zheng
$TTL 1D
@ IN SOA @ admin.baidu.com. (1 #此处版本号+11M1M3M1M )NS dns.baidu.com.NS slave.baidu.com.
dns A 192.168.75.129
www A 192.168.75.130
ftp A 192.168.75.132
slave A 192.168.75.131
aaa A 192.168.75.101 #此处新增一条正向解析
w CNAME www#2、反向解析
[root@oula1 ~]# vim /var/named/master.baidu.fan
$TTL 1D
@ IN SOA @ admin.baidu.com. (1 #此处版本号+11M1M3M1M )NS dns.baidu.com.NS slave.baidu.com.
129 PTR dns.baidu.com.
130 PTR www.baidu.com.
133 PTR w.baidu.com.
132 PTR ftp.baidu.com.
131 PTR slave.baidu.com.
101 PTR aaa.baidu.com. #此处新增一条反向解析#重启服务
[root@oula1 ~]# systemctl restart named2、测试
在从DNS服务器中提前输入tail -f /var/log/messages,即可观察到版本信息的变化
相关文章:

系统配置dns主从服务器
一、准备两台主机,区分主从 二、完全区域传送 1、主DNS服务器配置 #安装相关的包 [rootoula1 ~]# yum install bind -y#关闭防火墙 [rootoula1 ~]# systemctl stop firewalld [rootoula1 ~]# setenforce 0#修改配置主文件 [rootoula1 ~]# vim /etc/named.conf opt…...

【git】解决网络连接问题
ssh: connect to host github.com port 22: Connection timed out $ ssh: connect to host github.com port 22: Connection timed out fatal: Could not read from remote repository. bash: ssh:: command not found bash: fatal:: command not found无效 检查网络…...

限制API接口访问速率
文章目录 依赖注解aophelperTest 免责声明:本人无意侵权,奈何找不到原文作者,也找不到网址,于是自己记录一下,如果有侵权之嫌,请联系我删除文章 依赖 <!-- https://mvnrepository.com/artifact/com.goo…...

广东省第三届职业技能大赛“网络安全项目”B模块--数字取证解析
广东省第三届职业技能大赛“网络安全项目”B模块任务书 PS: 关注鱼影安全第一部分 网络安全事件响应第二部分 数字取证调查任务 3: 网络数据包分析取证解析:第三部分 应用程序安全:需要环境可以私信博主~PS: 关注鱼影安全 模块 B 竞赛项目试题 本文件为:广东省第三届职业技…...

全链路压力测试:现代软件工程中的重要性
全链路压力测试不仅可以确保系统在高负载下的性能和稳定性,还能帮助企业进行有效的风险管理和性能优化。在快速发展的互联网时代,全链路压力测试已成为确保软件产品质量的关键步骤。 1、测试环境搭建 测试应在与生产环境尽可能相似的环境中进行ÿ…...

【计算机网络】难点、易遗忘点总结
文章目录 1. 单工通信、半双工通信和全双工通信2. TCP的三次握手和四次挥手 1. 单工通信、半双工通信和全双工通信 主要区别在于信息传输的方向和时间安排。单工通信是指信息只能在一个方向上传输的通信方式。半双工通信允许信息在两个方向上传输,但在任何给定的时…...

谷达冠楠科技:抖音开网店新手小白可以卖的产品
随着互联网的发展,越来越多的人选择在网上开设自己的店铺。而抖音作为目前最火的短视频平台,也提供了开店的功能。那么,对于新手小白来说,抖音开网店可以卖哪些产品呢? 我们可以考虑的是服装类商品。抖音上有很多时尚博主&#x…...
爬虫案例—根据四大名著书名抓取并存储为文本文件
爬虫案例—根据四大名著书名抓取并存储为文本文件 诗词名句网:https://www.shicimingju.com 目标:输入四大名著的书名,抓取名著的全部内容,包括书名,作者,年代及各章节内容 诗词名句网主页如下图&#x…...
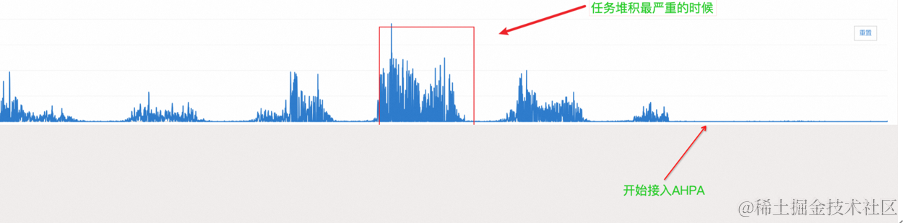
阿里云容器服务助力万兴科技 AIGC 应用加速
作者:子白(顾静) 2023 年堪称是 AIGC 元年,文生图领域诞生了 Stable Diffusion 项目,文生文领域诞生了 GPT 家族。一时间风起云涌,国内外许多企业投身 AIGC 创新浪潮,各大云厂商紧随其后纷纷推…...

STM32F103标准外设库——认识STM32(一)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:V…...
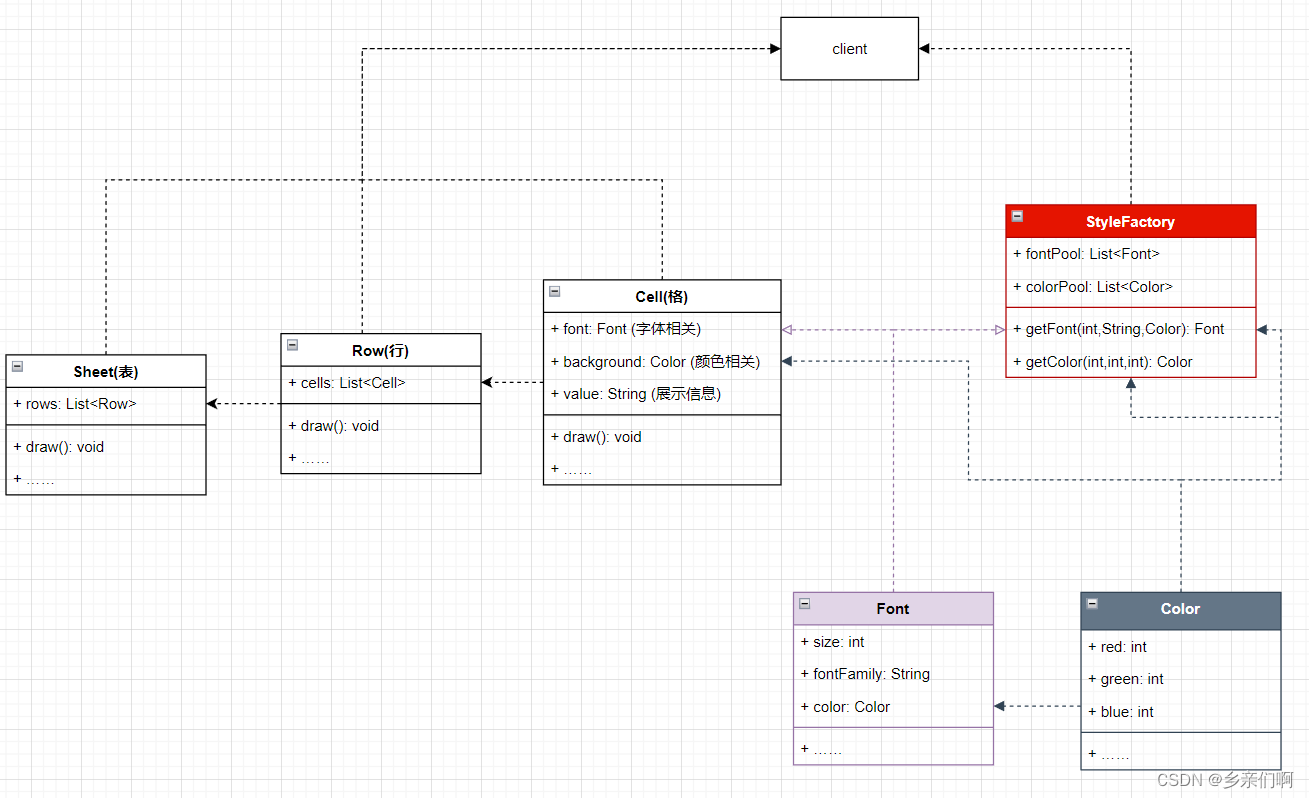
设计模式——1_5 享元(Flyweight)
今人不见古时月,今月曾经照古人 ——李白 文章目录 定义图纸一个例子:可以复用的样式表绘制表格降本增效?第一步,先分析 变化和不变的地方第二步,把变化和不变的地方拆开来第三步:有没有办法共享这些内容完…...
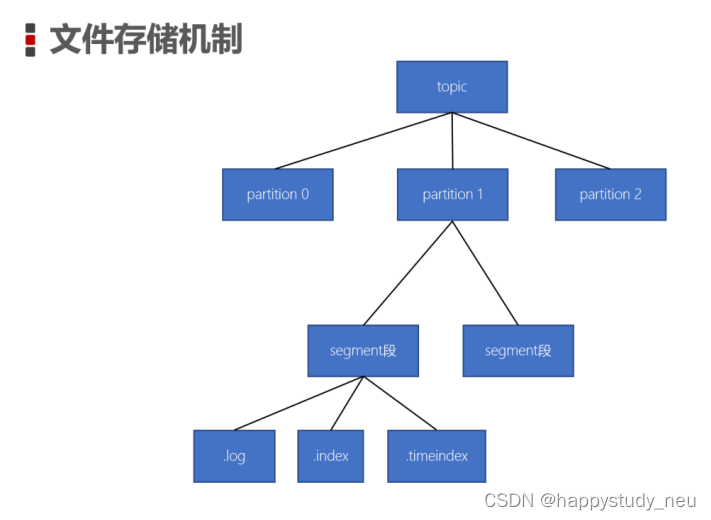
kafka系列(二)
本章承接kafka一内容,文章在本人博客主页都有,可以自行点击浏览。 幂等性 请求执行多次,但执行的结果是一致的。 如果,某个系统是不具备幂等性的,如果用户重复提交了某个表格,就可能会造成不良影响。例如…...
Ubuntu20.04安装配置OpenCV-Python库并首次执行读图
一、选择三方提供的预编译包安装: 可以从官网下载 OpenCV 的安装包,编译后使用;也可以直接使用第三方提供的预编译包 安装。显然后者不需要执行编译步骤,更便捷。选择由 PyPI 提供的 OpenCV 安装包,可以在 https://py…...

经典目标检测YOLO系列(二)YOLOV2的复现(2)正样本的匹配、损失函数的实现及模型训练
经典目标检测YOLO系列(二)YOLOV2的复现(2)正样本的匹配、损失函数的实现及模型训练 我们在之前实现YOLOv1的基础上,加入了先验框机制,快速的实现了YOLOv2的网络架构,并且实现了前向推理过程。 经典目标检测YOLO系列(二)YOLOV2的复现(1)总体…...

半波整流电路原理详解+参数与计算公式
什么是半波整流电路? 半波整流电路的基本操作非常简单,输入信号通过二极管,由于只能通过一个方向的电流,二极管的整流作用,单个二极管只允许通过一半的波形。 下图说明了半波整流电路的基本原理。 半波整流电路工作图…...
GZ036 区块链技术应用赛项赛题第3套
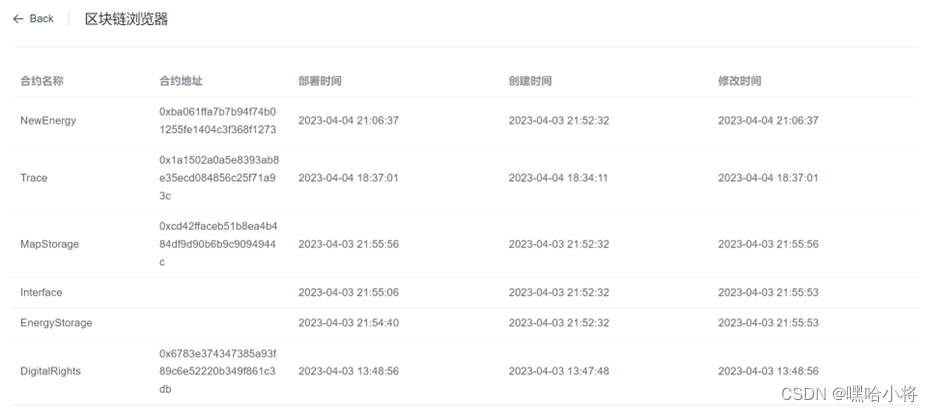
2023年全国职业院校技能大赛 高职组 “区块链技术应用” 赛项赛卷(3卷) 任 务 书 参赛队编号: 背景描述 新能源作为新兴领域,产业呈现碎片化与复杂化的特性,逐渐出现管理困难、供应链金融、可信监管与数…...
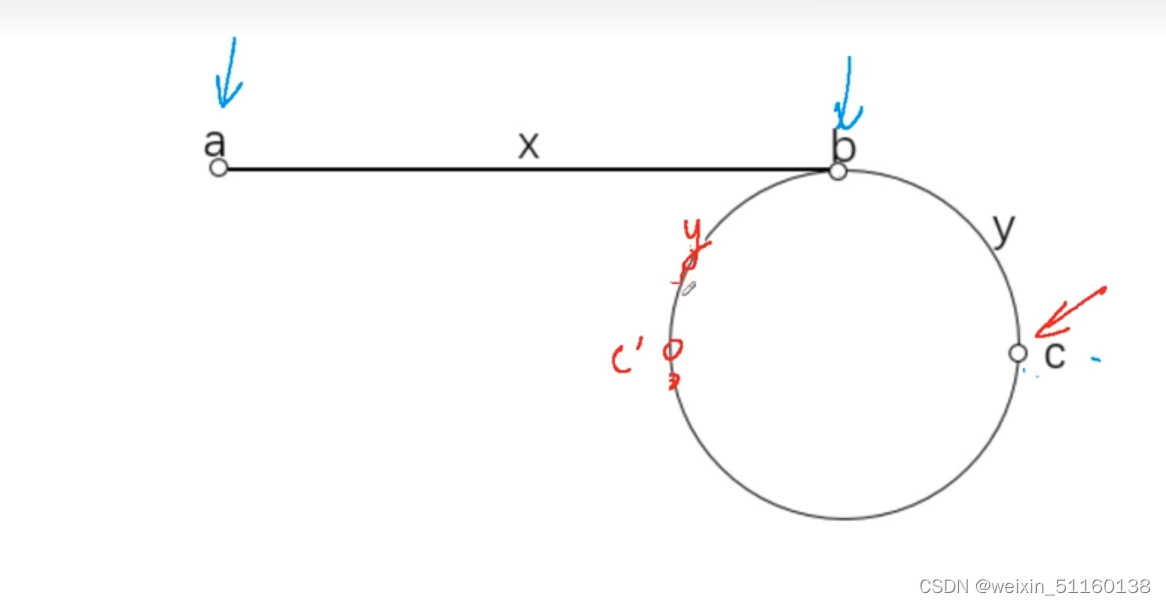
LeetCode142.环形链表II
力扣题目链接 思路:判断链表是否有环?可以使用快慢指针法,快指针每次走两步,慢指针每次走一步,如果链表有环一定会在环中相遇。 如何找环的入口?当快慢指针在环中第一次相遇时,让快指针从头结…...
触摸按键控制LED灯
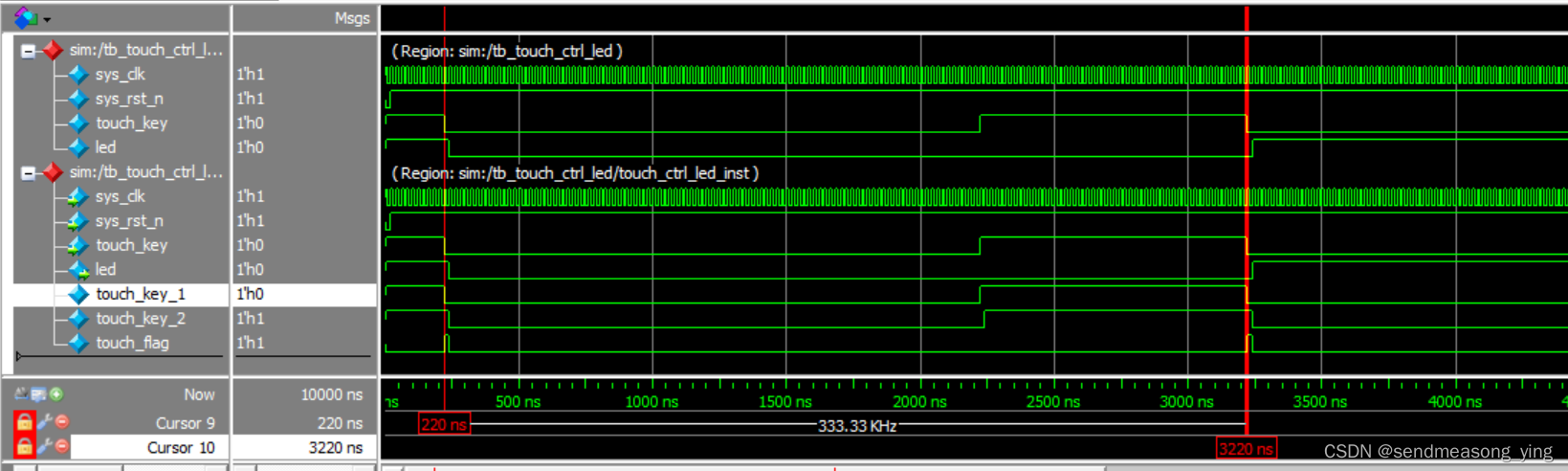
目录 1.理论 2.代码 2.1 touch_ctrl_led.v 2.2 tb_touch_ctrl_led 1.理论 以上的波形图的touch_flag是采用组合逻辑的方式产生的。 以上的touch_flag是采用时序逻辑产生的,时序逻辑会延迟一拍。 以上是上升沿和下降沿的组合逻辑和时序逻辑实现,逻辑或…...
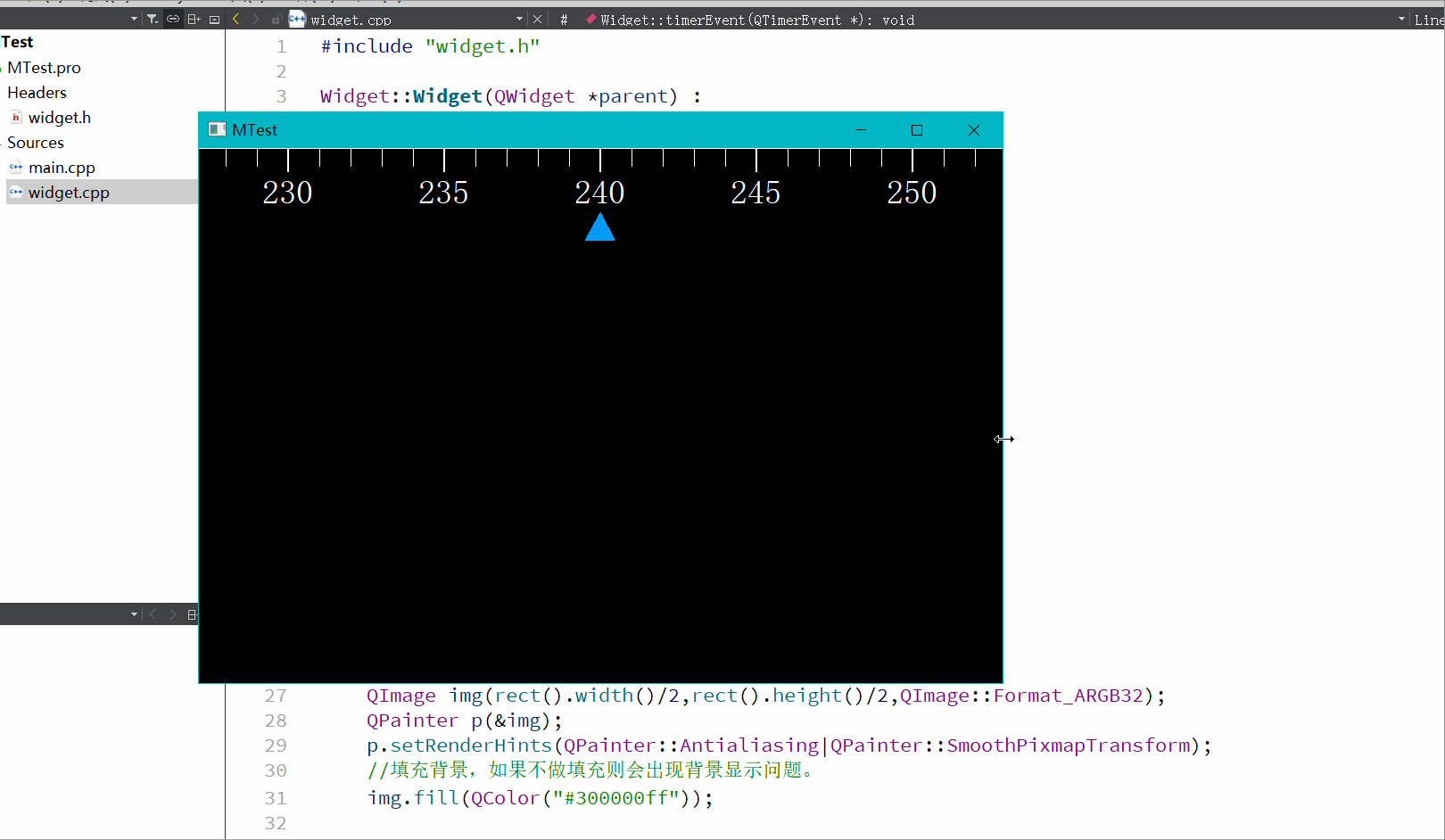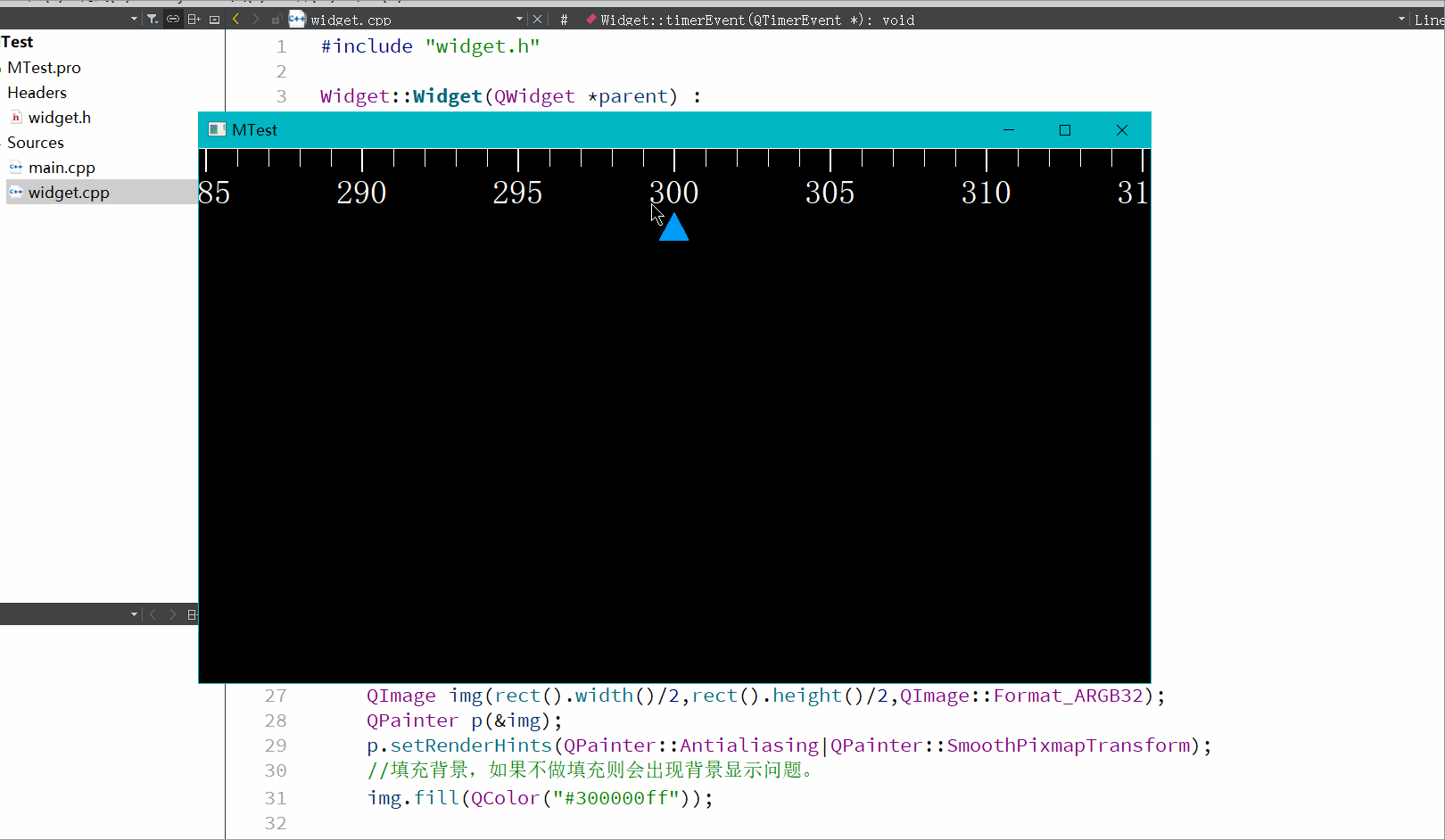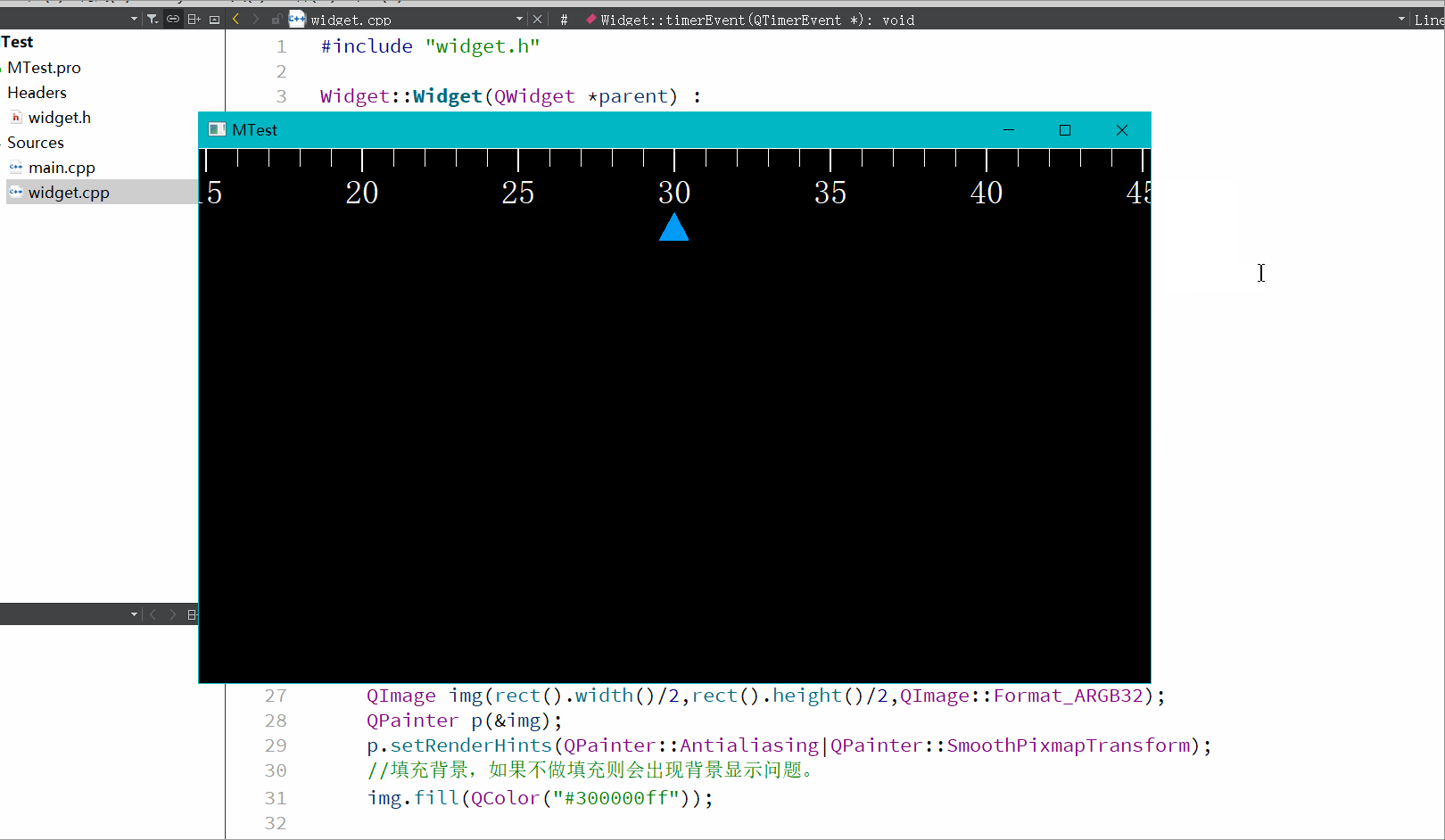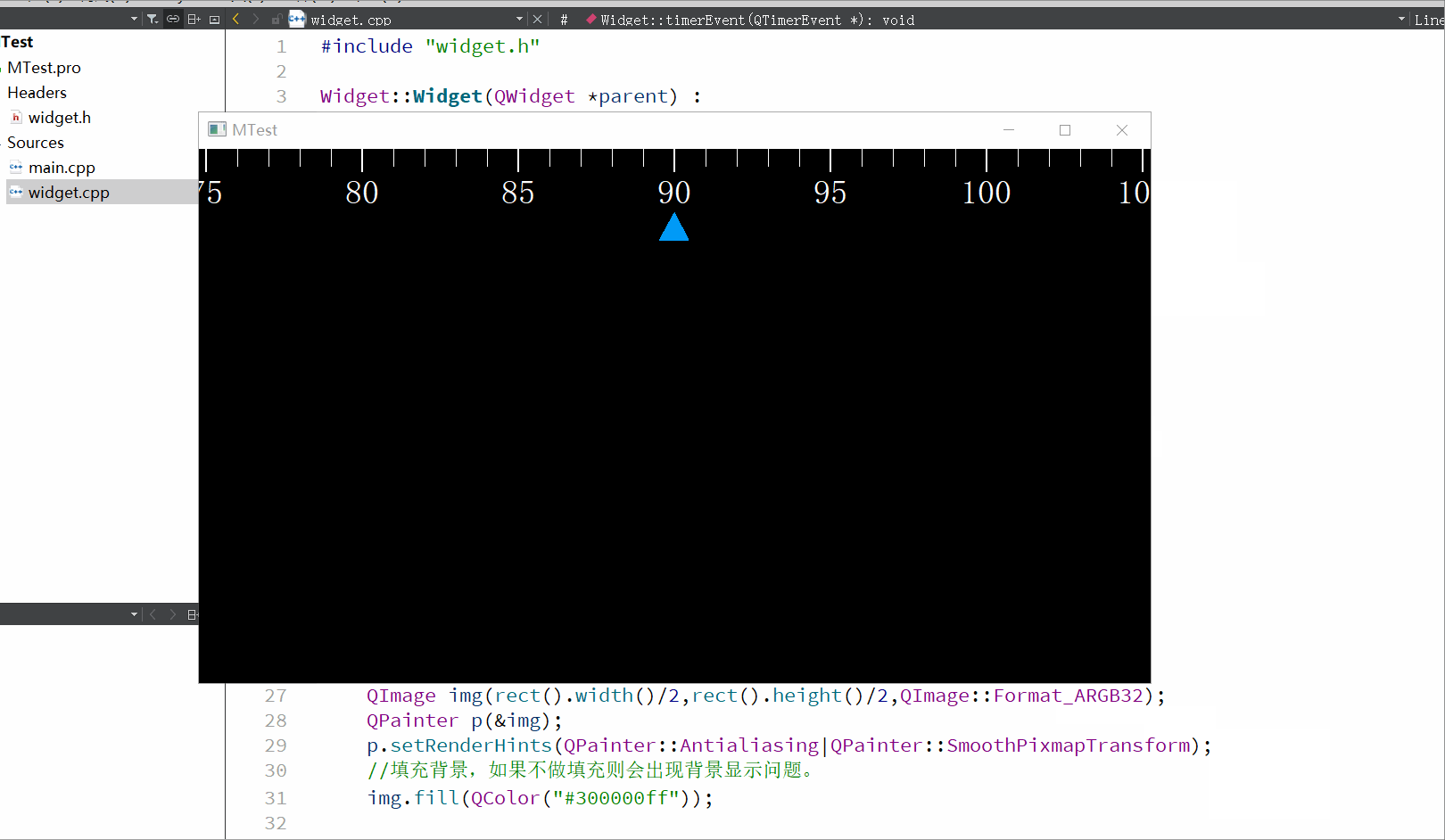
QT自定义控件0-360°刻度尺
支持0到360,360到0的过度。 直接上代码,可以直接用,使用的paintevent事件实现的,没啥好讲的。 .cpp void Widget::drawCourse(QPainter& p,QPen pen,QFont font) {double currentNumber m_ang;p.setBrush(Qt::black);p.dra…...

c语言0基础笔记
目录 前言 第01章_C语言入门 1.1初识计算机语言 1.2初识C语言 1.3第一个c程序 1.4IDE使用 1.5注释 1.6第一个c程序剖析 1.7printf()输出格式 第02章_变量与进制 2.1关键字 2.2标识符 2.3变量 2.4基本数据类型的使用 2.5变量间的运算规则 2.6常量 2.7输入/输出函…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
