【算法优选】 动态规划之简单多状态dp问题——壹
文章目录
- 🎋前言
- 🎍[按摩师](https://leetcode.cn/problems/the-masseuse-lcci/)
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现
- 🍀[打家劫舍二](https://leetcode.cn/problems/house-robber-ii/description/)
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现
- 🎍[删除并获得点数](https://leetcode.cn/problems/delete-and-earn/description/)
- 🚩题目描述
- 🚩算法思路
- 🚩代码实现
- ⭕总结
🎋前言
动态规划相关题目都可以参考以下五个步骤进行解答:
-
状态表⽰
-
状态转移⽅程
-
初始化
-
填表顺序
-
返回值
后面题的解答思路也将按照这五个步骤进行讲解。
🎍按摩师
🚩题目描述
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
注意:本题相对原题稍作改动
- 示例 1:
输入: [1,2,3,1]
输出: 4
解释: 选择 1 号预约和 3 号预约,总时长 = 1 + 3 = 4。 - 示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 选择 1 号预约、 3 号预约和 5 号预约,总时长 = 2 + 9 + 1 = 12。 - 示例 3:
输入: [2,1,4,5,3,1,1,3]
输出: 12
解释: 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约,总时长 = 2 + 4 + 3 + 3 = 12。
class Solution {public int massage(int[] nums) {}
}
🚩算法思路:
- 状态表⽰:
对于简单的线性 dp ,我们可以⽤「经验+题⽬要求」来定义状态表⽰:
- 以某个位置为结尾;
- 以某个位置为起点。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
dp[i] 表⽰:选择到 i 位置时,此时的最⻓预约时⻓。
但是我们这个题在 i 位置的时候,会⾯临「选择」或者「不选择」两种抉择,所依赖的状态需要细分:
- f[i] 表⽰:选择到 i 位置时, nums[i] 必选,此时的最⻓预约时⻓;
- g[i] 表⽰:选择到 i 位置时, nums[i] 不选,此时的最⻓预约时⻓。
- 状态转移⽅程:
因为状态表⽰定义了两个,因此我们的状态转移⽅程也要分析两个:
对于 f[i] :
- 如果 nums[i] 必选,那么我们仅需知道 i - 1 位置在不选的情况下的最⻓预约时⻓,然后加上 nums[i] 即可,因此 f[i] = g[i - 1] + nums[i] 。
对于 g[i] :
- 如果 nums[i] 不选,那么 i - 1 位置上选或者不选都可以。因此,我们需要知道 i- 1 位置上选或者不选两种情况下的最⻓时⻓,因此g[i] = max(f[i - 1], g[i- 1]) 。
-
初始化:
这道题的初始化⽐较简单,因此⽆需加辅助节点,仅需初始化 f[0] = nums[0], g[0] = 0 即可。 -
填表顺序
根据「状态转移⽅程」得「从左往右,两个表⼀起填」。 -
返回值
根据「状态表⽰」,应该返回 max(f[n - 1], g[n - 1]) 。
🚩代码实现
class Solution
{public int massage(int[] nums){// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int n = nums.length;if(n == 0) return 0; // 处理边界条件int[] f = new int[n];int[] g = new int[n];f[0] = nums[0];for(int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = Math.max(f[i - 1], g[i - 1]);}return Math.max(g[n - 1], f[n - 1]);}
}
当然博主这里还提供另一种解题方法,就不讲解了,直接给出代码,代码如下:
class Solution {public int massage(int[] nums) {int len = nums.length;if(len == 0) {return 0;}if(len == 1) {return nums[0];}int[] dp = new int[len + 1];dp[1] = nums[0];dp[2] = nums[1];for(int i = 3; i <= len ; i++) {int max = Math.max(dp[i-2],dp[i-3]);dp[i] = nums[i-1] + max;}return Math.max(dp[len-1],dp[len]);}
}
🍀打家劫舍二
🚩题目描述
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
- 示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。 - 示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。 - 示例 3:
输入:nums = [1,2,3]
输出:3
🚩算法思路:
这⼀个问题是「打家劫舍I」问题的变形。
上⼀个问题是⼀个「单排」的模式,这⼀个问题是⼀个「环形」的模式,也就是⾸尾是相连的。但是我们可以将「环形」问题转化为「两个单排」问题:
- 偷第⼀个房屋时的最⼤⾦额x ,此时不能偷最后⼀个房⼦,因此就是偷 [0, n - 2] 区间的房⼦;
- 不偷第⼀个房屋时的最⼤⾦额 y ,此时可以偷最后⼀个房⼦,因此就是偷 [1, n - 1] 区间的房⼦;
两种情况下的「最⼤值」,就是最终的结果。
因此,问题就转化成求「两次单排结果的最⼤值」。
🚩代码实现
class Solution
{public int rob(int[] nums) {int n = nums.length;return Math.max(nums[0] + rob1(nums, 2, n - 2), rob1(nums, 1, n - 1));}public int rob1(int[] nums, int left, int right) {if(left > right) return 0;// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回int n = nums.length;int[] f= new int[n];int[] g= new int[n];f[left] = nums[left];for(int i = left + 1; i <= right; i++){f[i] = g[i - 1] + nums[i];g[i] = Math.max(g[i - 1], f[i - 1]);}return Math.max(f[right], g[right]);}
}
🎍删除并获得点数
🚩题目描述
给你一个整数数组 nums ,你可以对它进行一些操作。
每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
- 示例 1:
输入:nums = [3,4,2]
输出:6
解释:
删除 4 获得 4 个点数,因此 3 也被删除。之后,删除 2 获得 2 个点数。总共获得 6 个点数。 - 示例 2:
输入:nums = [2,2,3,3,3,4]
输出:9
解释:
删除 3 获得 3 个点数,接着要删除两个 2 和 4 。之后,再次删除 3 获得 3 个点数,再次删除 3 获得 3 个点数。总共获得 9 个点数。
class Solution {public int deleteAndEarn(int[] nums) {}
}
🚩算法思路
其实这道题依旧是「打家劫舍I」问题的变型。
我们注意到题⽬描述,选择 x 数字的时候, x - 1 与 x + 1 是不能被选择的。像不像「打家劫舍」问题中,选择 i 位置的⾦额之后,就不能选择 i - 1 位置以及 i + 1 位置的⾦额呢~
因此,我们可以创建⼀个⼤⼩为 10001 (根据题⽬的数据范围)的 hash 数组,将nums 数
组中每⼀个元素 x ,累加到 hash 数组下标 x 的位置处,然后在 hash 数组上来⼀次「打家劫舍」即可
🚩代码实现
class Solution {public int deleteAndEarn(int[] nums) {int[] arr = new int[10001];for(int i = 0; i < nums.length; i++) {arr[nums[i]] += nums[i];}int[] f= new int[10001];int[] g= new int[10001];f[0] = arr[0];for(int i = 1; i < 10001; i++){f[i] = g[i - 1] + arr[i];g[i] = Math.max(g[i - 1], f[i - 1]);}return Math.max(f[10000], g[10000]);}
}
⭕总结
关于《【算法优选】 动态规划之简单多状态dp问题——壹》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【算法优选】 动态规划之简单多状态dp问题——壹
文章目录 🎋前言🎍[按摩师](https://leetcode.cn/problems/the-masseuse-lcci/)🚩题目描述🚩算法思路:🚩代码实现 🍀[打家劫舍二](https://leetcode.cn/problems/house-robber-ii/description/)…...
Git学习笔记(第2章):Git安装
官网地址:Githttps://git-scm.com/ Step1:查看Git的GNU协议 → 点击“Next” Step2:设置Git的安装位置(非中文、无空格的目录) → 点击“Next” Step3:选择Git的选项配置(推荐默认设置) → 点击“Next” Step4:设置Git…...

C生万物呀
1、快捷键 快捷键描述ctrl滚轮字体变大小ctrlKC注释ctrlKU取消注释home行首end行末 2、C语言标准库函数 stdio.h:包含了输入输出相关的函数,如printf()、scanf()、fgets()等。 stdlib.h:包含了通用工具函数,如malloc()、free()…...

华纳云:怎么解决docker容器一直处于重启状态的问题?
Docker容器一直处于重启状态可能是由于容器内部的问题导致的。以下是一些建议,帮助你解决这个问题: 查看容器日志: 使用以下命令查看容器的日志,以便获取更多信息: docker logs 查看日志可能会提供容器启动时的错误信息…...
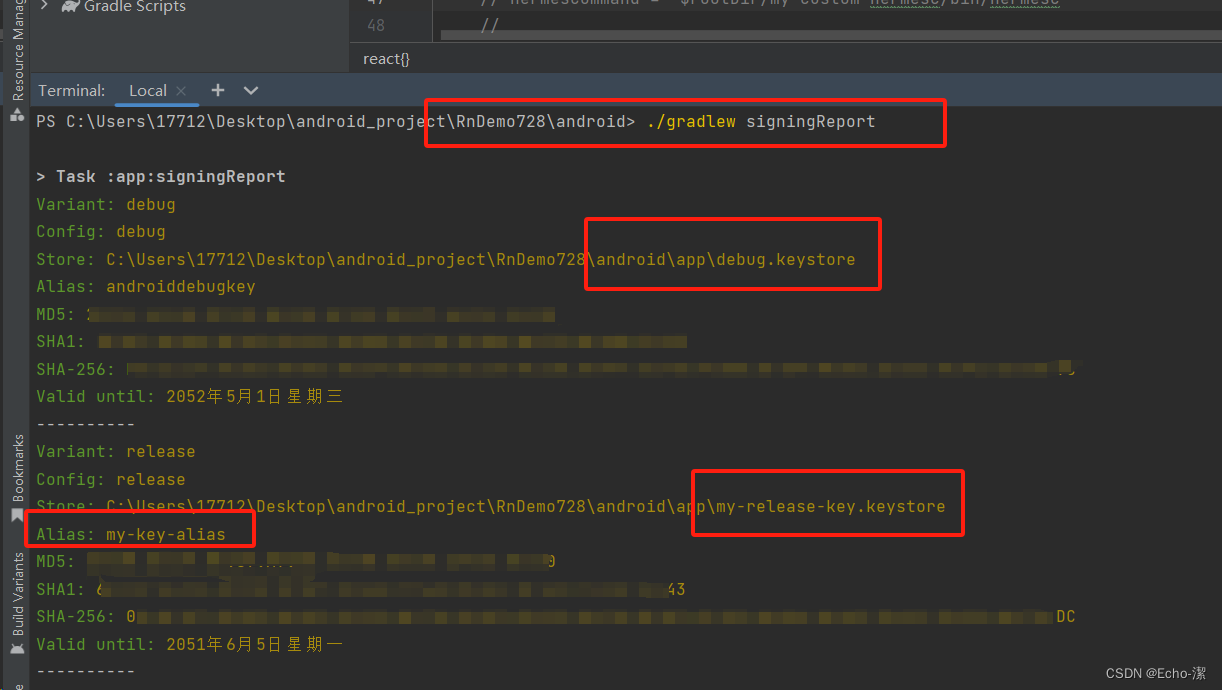
react native android使用命令生成打包签名密钥
一、概述 Android 要求所有应用都有一个数字签名才会被允许安装在用户手机上,所以在把应用发布到应用市场之前,你需要先生成一个签名的 AAB 或 APK 包(Google Play 现在要求 AAB 格式,而国内的应用市场目前仅支持 APK 格式。但无论…...
】内存冷热标记(JavaPythonC++JS实现))
245.【2023年华为OD机试真题(C卷)】内存冷热标记(JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-内存冷热标记二.解题思路三.题解代码Python题解…...
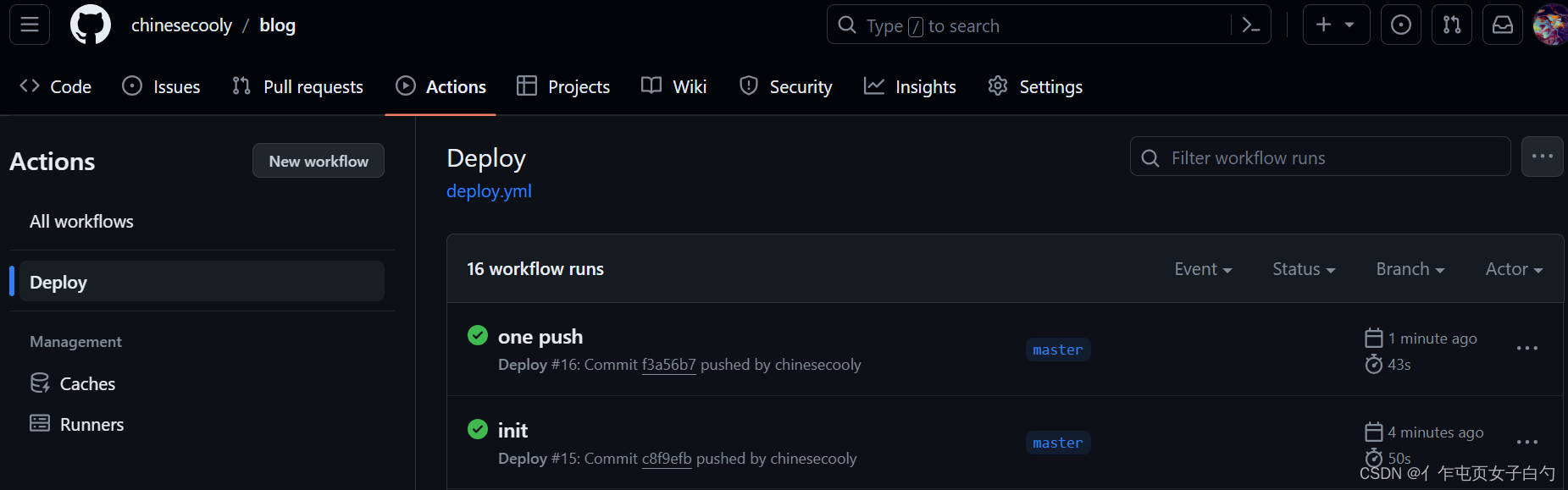
Docker五部曲之五:通过Docker和GitHub Action搭建个人CICD项目
文章目录 项目介绍Dockerfile解析compose.yml解析Nginx反向代理到容器以及SSL证书设置MySQL的准备工作Spring和环境变量的交互 GitHub Action解析项目测试结语 项目介绍 该项目是一个入门CICD-Demo,它由以下几部分组成: Dockerfile:用于构建…...

「JavaSE」类和对象3
🎇个人主页:Ice_Sugar_7 🎇所属专栏:快来卷Java啦 🎇欢迎点赞收藏加关注哦! 类和对象3 🍉多态🍌重写🍌向上转型&向下转型🍌静态绑定&动态绑定&#x…...
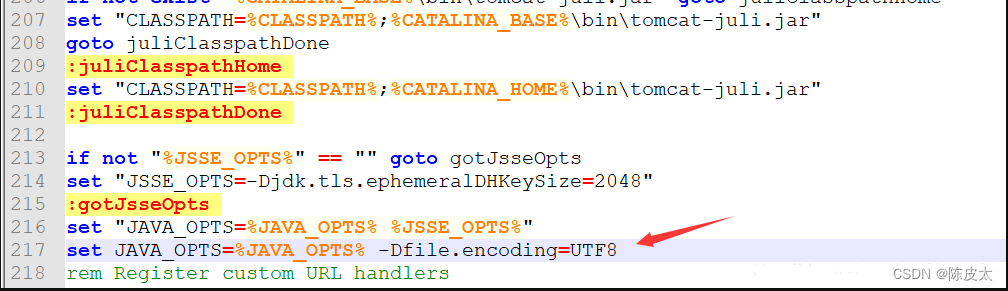
IntelliJ IDEA 中输出乱码解决
最近tomcat突然在控制台输出乱码,各种乱码问题,查阅大量的资料,最终得以解决. IDEA控制台输出乱码 问题一:idea中tomcat控制台输出乱码 运行本地的tomcat\bin\start.bat文件页面显示正常 在idea中显示乱码 解决: 根…...
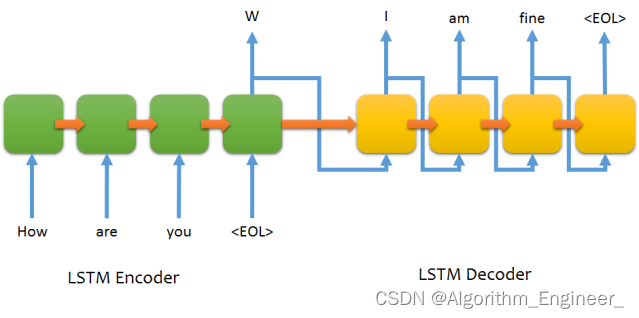
序列到序列模型
一.序列到序列模型的简介 序列到序列(Sequence-to-Sequence,Seq2Seq)模型是一类用于处理序列数据的深度学习模型。该模型最初被设计用于机器翻译,但后来在各种自然语言处理和其他领域的任务中得到了广泛应用。 Seq2Seq模型的核…...
复习提纲4)
计算机网络(第六版)复习提纲4
计算机网络的体系结构: 三类体系结构: OSI七层:物理层比特位传输,链路层相邻链路传输检验,网络层进行路由选择,运输层实现端到端进程通信,会话层连接管理,表示层数据格式,…...

天拓分享:汽车零部件制造企业如何利用边缘计算网关和数网星平台实现数控机床数据采集分析
一、项目背景 某汽车零部件制造企业为了提高生产效率、降低能耗和提高产品质量,决定引入TDE边缘计算网关和数网星工业互联网平台,对数控机床进行数据采集与分析。 二、解决方案 1、设备选型与配置:考虑到企业生产需求和数控机床的特性&…...
爬虫逆向开发教程1-介绍,入门案例
爬虫前景 在互联网的世界里,数据就是新时代的“黄金”。而爬虫,就是帮助我们淘金的“工具”。随着互联网的不断发展,数据量呈现指数级的增长,在数据为王的时代,有效的挖掘数据和利用,你会得到更多东西。 学…...
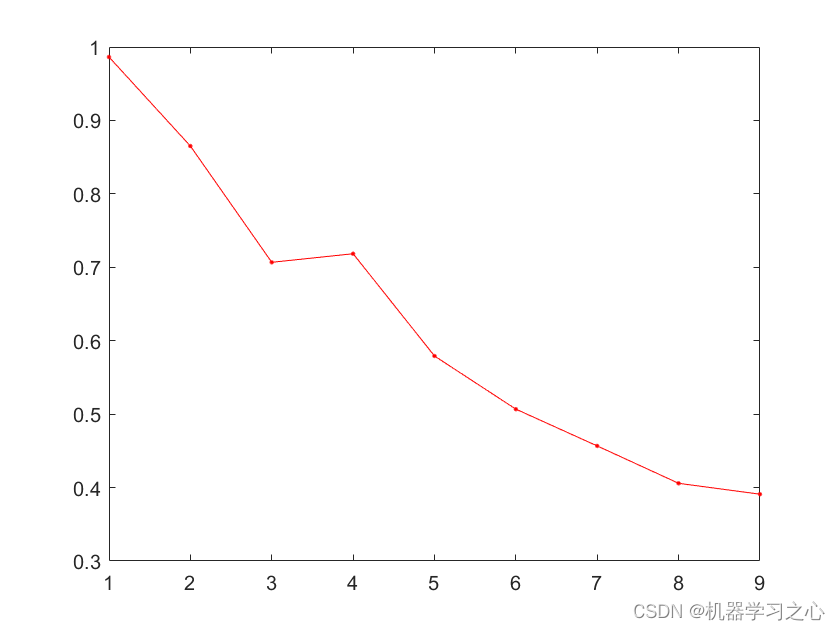
时序分解 | Matlab实现CEEMDAN+PE自适应噪声完备集合经验模态分解+排列熵计算
时序分解 | Matlab实现CEEMDANPE自适应噪声完备集合经验模态分解排列熵计算 目录 时序分解 | Matlab实现CEEMDANPE自适应噪声完备集合经验模态分解排列熵计算效果一览基本介绍程序设计参考资料 效果一览 基本介绍 CEEMDANPE自适应噪声完备集合经验模态分解排列熵计算 运行环境m…...

Oracle命令大全
文章目录 1. SQL*Plus命令(用于连接与管理Oracle数据库)2. SQL数据定义语言(DDL)命令3. SQL数据操作语言(DML)命令4. PL/SQL程序块5. 系统用户管理6. 数据备份与恢复相关命令1. SQL*Plus命令(用…...
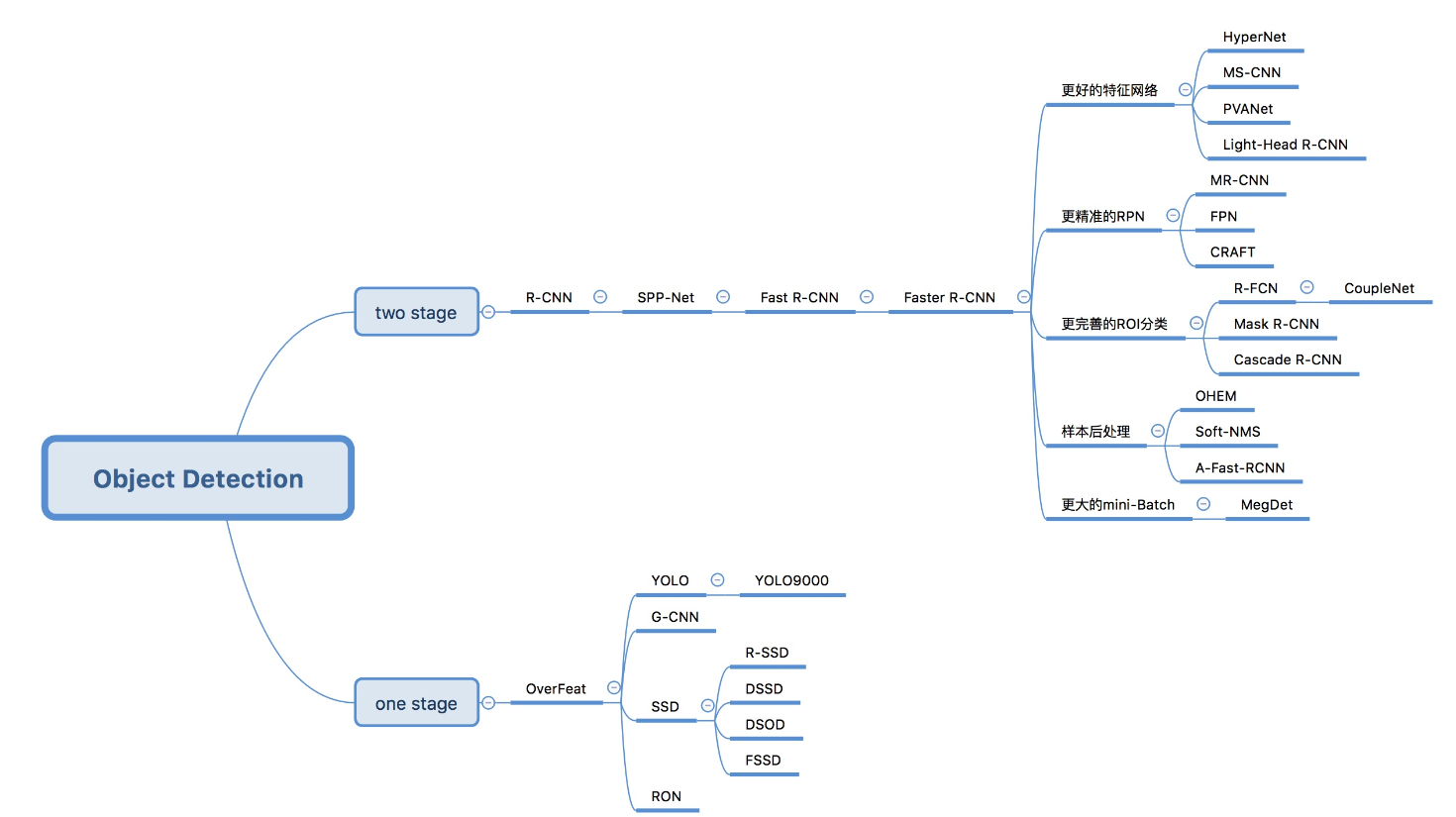
目标检测--01
基本概念 什么是目标检测? 目标检测(Object Detection)的任务是找出图像中所有感兴趣的目标(物体),确定它们的类别和位置,是计算机视觉领域的核心问题之一。由于各类物体有不同的外观、形状…...

MyBatisPlus学习笔记三-核心功能
接上篇: MyBatisPlus学习笔记二-CSDN博客 1、核心功能-IService开发基础业务接口 1.1、介绍 1.2、引用依赖 1.3、配置文件 1.4、用例-新增 1.5、用例-删除 1.6、用例-根据id查询 1.7、用例-根据ids查询 2、核心功能-IService开发复杂业务接口 2.1、实例-更新 3、…...

【并发编程系列】putIfAbsent和getOrDefault用法
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
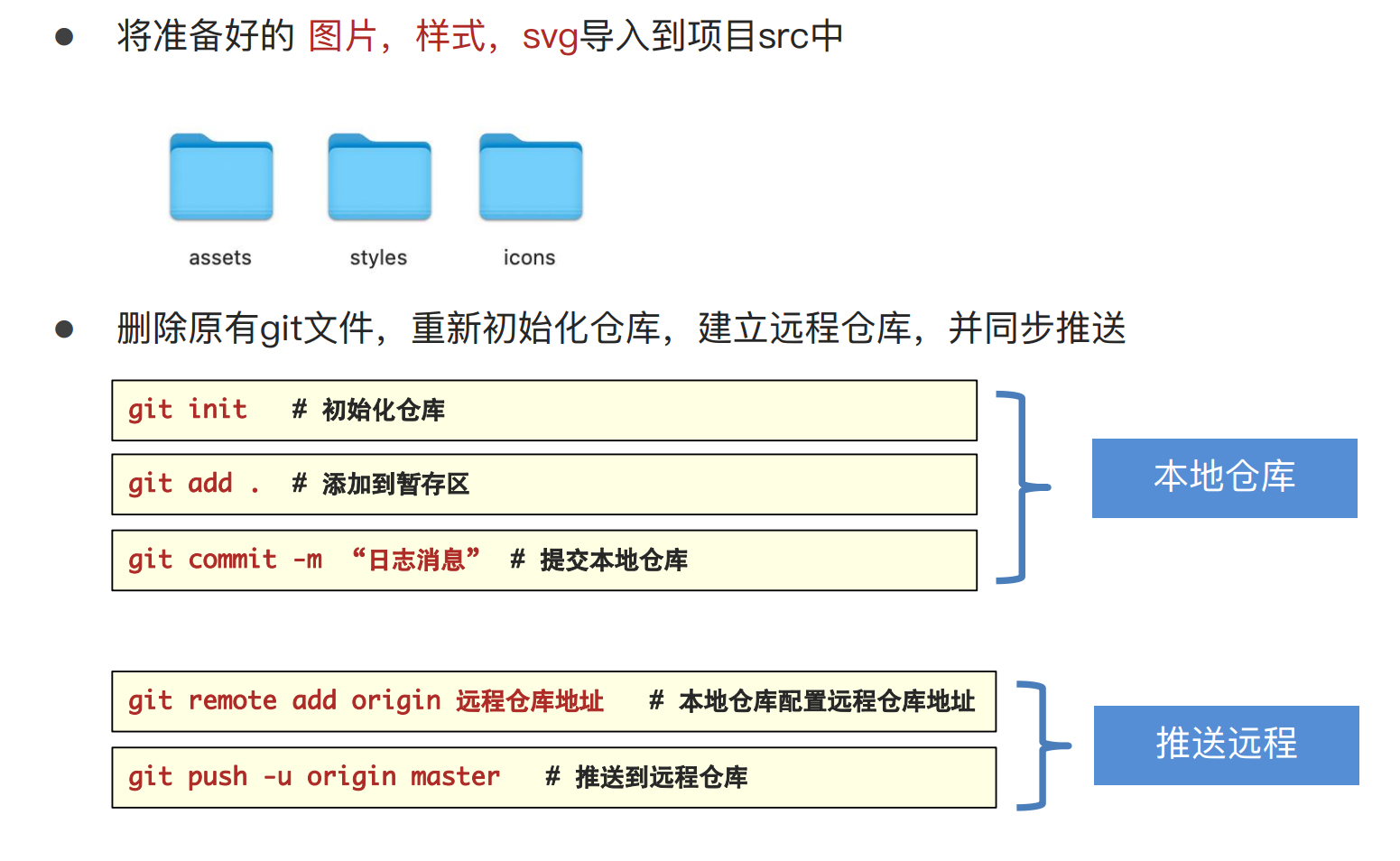
人力资源智能化管理项目(day01:基础架构拆解)
学习源码可以看我的个人前端学习笔记 (github.com):qdxzw/frontlearningNotes 觉得有帮助的同学,可以点心心支持一下哈 一、基础架构拆解 1.拉取模板代码 git clone GitHub - PanJiaChen/vue-admin-template: a vue2.0 minimal admin template 项目名 2.core-js…...

JAVA ORM Bee的设计模式分析
创建型 工厂模式(Factory Pattern) 日志工厂 LoggerFactory 静态工厂模式 *(Static Factory) BeeFactoryHelper 单例模式(Singleton Pattern) 使用单例模式管理系统的配置信息 HoneyConfig 建…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
