有序矩阵中第 K 小的元素
题目链接
有序矩阵中第 K 小的元素
题目描述
注意点
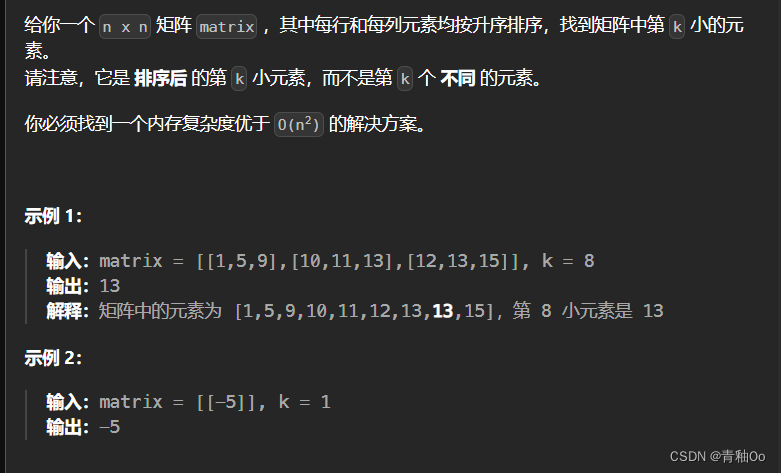
- 每行和每列元素均按升序排序
- 找到一个内存复杂度优于 O(n²) 的解决方案
解答思路
- 使用二分查找,思路为:
(1)因为左上角的元素值更小,右下角的元素值更大,先将left设置为左上角元素的值,right设置为右下角元素的值;
(2)判断不大于left和right中间值mid的元素数量sum;
(3)如果sum小于k,则将left设置为mid + 1,否则将right设置为mid。 - 不断重复上述过程,直到满足sum等于k时right的最小值,此时left等于right,且right是大于等于矩阵中K个元素的临界点,所以矩阵中一定会有一个元素等于right(否则说明并没有找到sum等于k时right的最小值),right也就是有序矩阵中第 K 小的元素
代码
class Solution {int n;public int kthSmallest(int[][] matrix, int k) {n = matrix.length;int left = matrix[0][0];int right = matrix[n - 1][n - 1];while (left < right) {int mid = left + (right - left) / 2;int sum = countLessThanMid(matrix, mid);if (sum < k) {left = mid + 1;} else {right = mid;}}return left;}public int countLessThanMid(int[][] matrix, int mid) {int sum = 0;for (int i = 0; i < n; i++) {// 如果左上角都大于mid,则一定没有小于等于mid的元素存在if (matrix[i][0] > mid) {return sum;}// 如果右上角都小于等于mid,则该行所有元素都小于等于midif (matrix[i][n - 1] <= mid) {sum += n;continue;}// 其余情况查找改行小于等于mid的元素for (int j = 0; j < n; j++) {if (matrix[i][j] > mid) {break;}sum++;}}return sum;}
}
关键点
- 二分查找的思路
- 怎么找到sum等于k时right的最小值
- 当right - left=1,且两个数都是负数的时候,求mid时会等于right的值,此时如果sum >= k,则会一直卡在循环中无法跳出,需要保证这种特殊情况求mid也是left,所以求mid时使用left + (right - left) / 2
相关文章:
有序矩阵中第 K 小的元素
题目链接 有序矩阵中第 K 小的元素 题目描述 注意点 每行和每列元素均按升序排序找到一个内存复杂度优于 O(n) 的解决方案 解答思路 使用二分查找,思路为: (1)因为左上角的元素值更小,右下角的元素值更大…...

Nginx详细介绍(并从技术层面深度剖析)
nginx介绍 1.nginx 介绍2.nginx的优势3.Nginx VS Apache3.1.内核、语言、诞生时间比较3.2.功能比较3.3.Nginx 相对 apache 的优点 4.Nginx为什么有这么多的优势?4.1.IO多路复用(I/O multiplexing【多并发】)4.2.nginx的驱动模型介绍4.3.nginx…...

单元测试基本概念
单元测试一般是开发来做的,但是因为业务需要也曾涉及过单元测试。目前就单元测试的基础概念做下总结。 一、 单元测试定义: 单元测试是软件开发中的一种测试方法,用于验证程序中的最小可测单元——即代码中的单个函数、方法或模块。单元测试…...
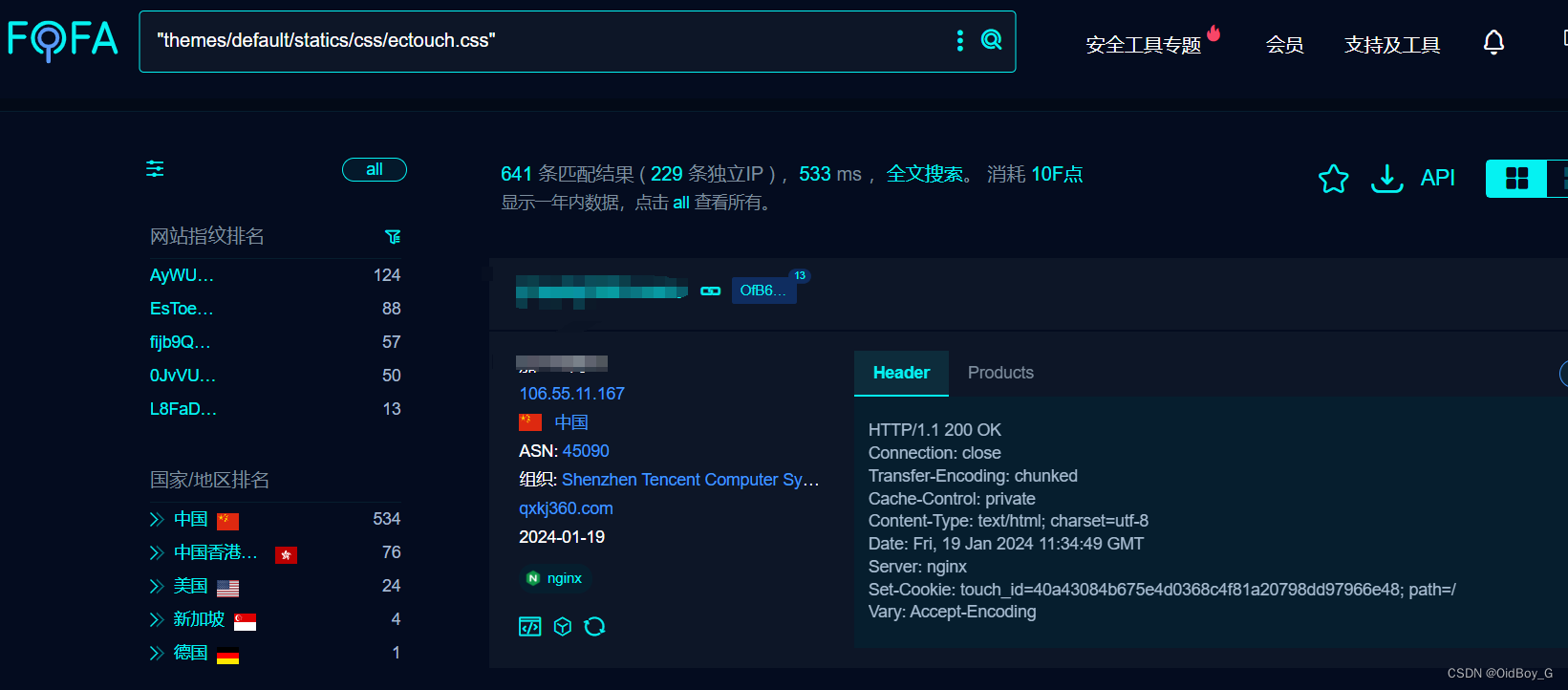
ECTouch 电商微信小程序 SQL注入漏洞复现(CVE-2023-39560)
0x01 产品简介 ECTouch是一款开源的电商系统,为中小企业提供最佳的新零售解决方案 0x02 漏洞概述 ECTouch 电商系统 /ectouch-main/include/apps/default/helpers/insert.php 文件中第285行的 insert_bought_notes 函数中,传入的 $arr[id] 参数未进行验证和过滤,导致未经…...
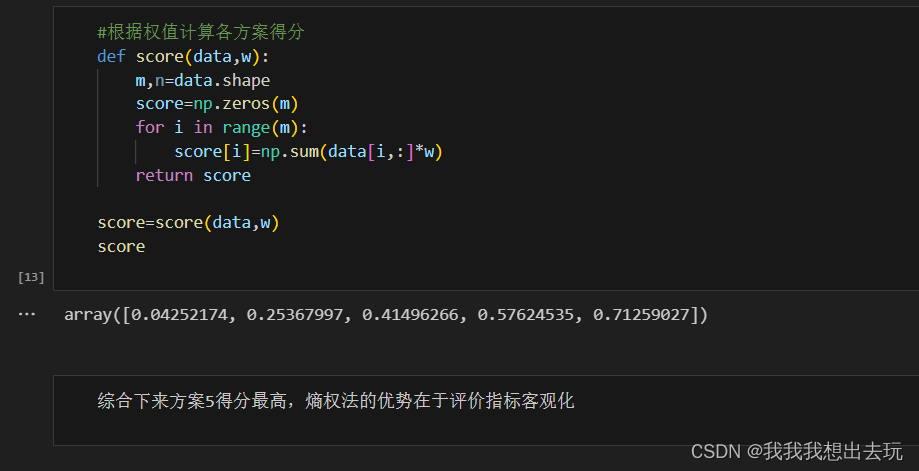
MCM备赛笔记——熵权法
Key Concept 熵权法是一种基于信息熵概念的权重确定方法,用于多指标决策分析中。信息熵是度量信息量的不确定性或混乱程度的指标,在熵权法中,它用来反映某个指标在评价过程中的分散程度,进而确定该指标的权重。指标的分散程度越高…...
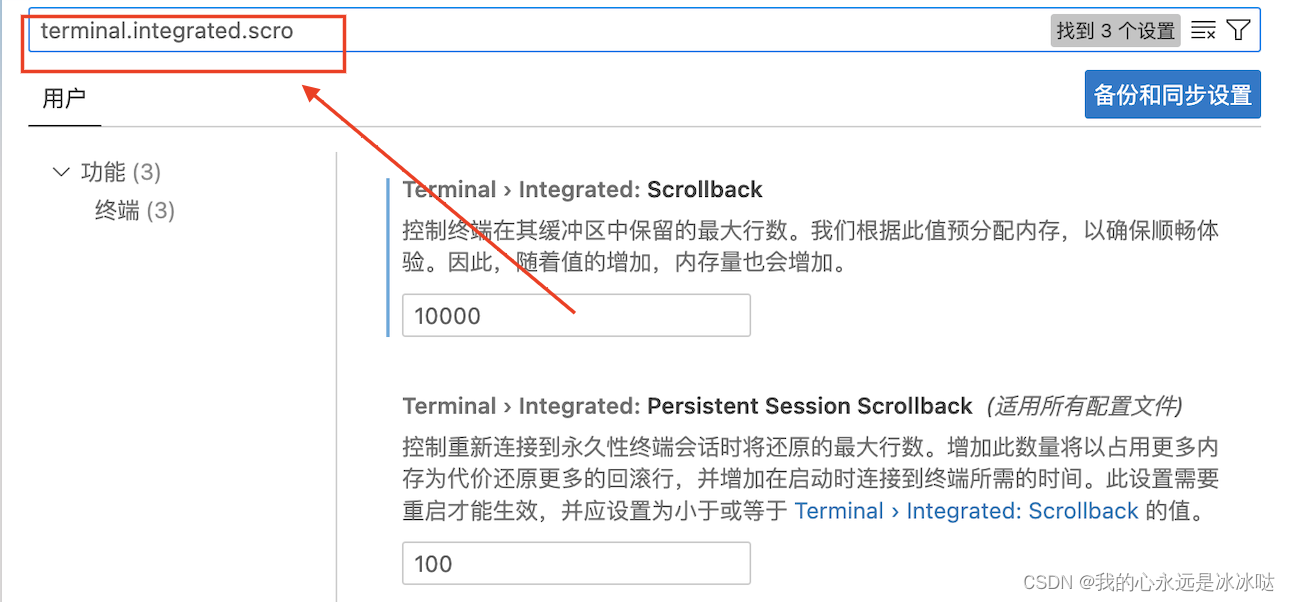
vscode设置terminal的最大行数
今天跑代码出现一个问题,就是整个程序跑完,整个程序的输出信息过多,最开始输出的信息已经被vscode的缓存冲掉了,只能看到最后的一部分,具体的原因是vscode的terminal默认只能保存1000行的信息,所以如果想保…...

kafka hang 问题记录
参考文档 https://cloud.tencent.com/developer/article/1821477 9092端口 端口9092通常与Apache Kafka关联。 Kafka是一个开源的分布式事件流平台,用于构建实时的数据管道和流应用。 它能够处理任意大小的数据,以容错的方式处理数据流。 在默认配置…...

Jmeter-BeanShell脚本中for循环里面使用random随机数函数,每次生成的都一样
预想的是每次循环生成的随机数不一样,但实际使用Random函数生成的是重复的。 以下是部分原代码: List updateList new ArrayList(); for(Object o: fieldList){Map map new HashMap();map.put("id", o.get("id"));map.put("…...

高级编程。JavaScript中有哪些类型转换机制?
一、概述 前面我们讲到,JS中有六种简单数据类型:undefined、null、boolean、string、number、symbol,以及引用类型:object 但是我们在声明的时候只有一种数据类型,只有到运行期间才会确定当前类型 let x y ? 1 : …...
Linux系统下常用软件安装汇总,包括mysql,java,git,redis等
01.环境搭建 1.安装列表 MySQL 5.7.11 Java 1.8 Apache Maven 3.6 tomcat8.5 git Redis Nginx python docker 2.安装mysql 1.拷贝mysql安装文件到Linux的某个目录下 2.解压Linux安装包:tar -xvzf mysql-5.7.32-linux-glibc2.12-x86_64.tar.gz 3.进入解压后…...
)
【Linux】——期末复习题(一)
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...

【论文阅读】Speech Driven Video Editing via an Audio-Conditioned Diffusion Model
DiffusionVideoEditing:基于音频条件扩散模型的语音驱动视频编辑 code:GitHub - DanBigioi/DiffusionVideoEditing: Official project repo for paper "Speech Driven Video Editing via an Audio-Conditioned Diffusion Model" paper&#…...
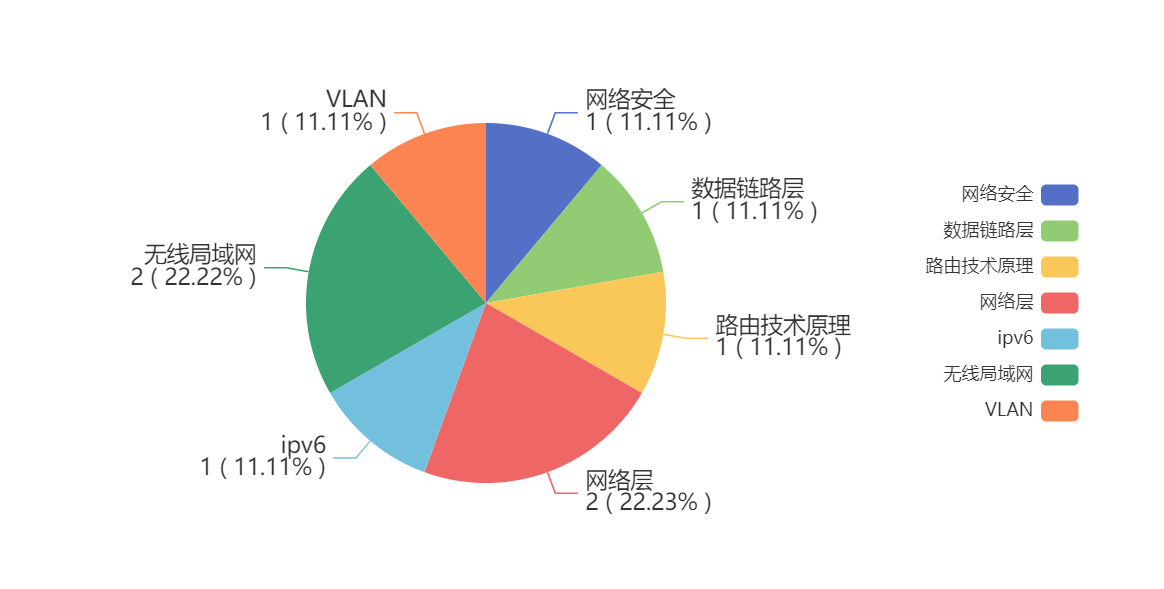
【华为 ICT HCIA eNSP 习题汇总】——题目集4
1、(多选)网络中出现故障后,管理员通过排查发现某台路由器的配置被修改了,那么管理员应该采取哪些措施来避免这种状况再次发生? A、管理员应该通过配置 ACL 来扩展只有管理员能够登录设备 B、管理员应该在路由的管理端…...
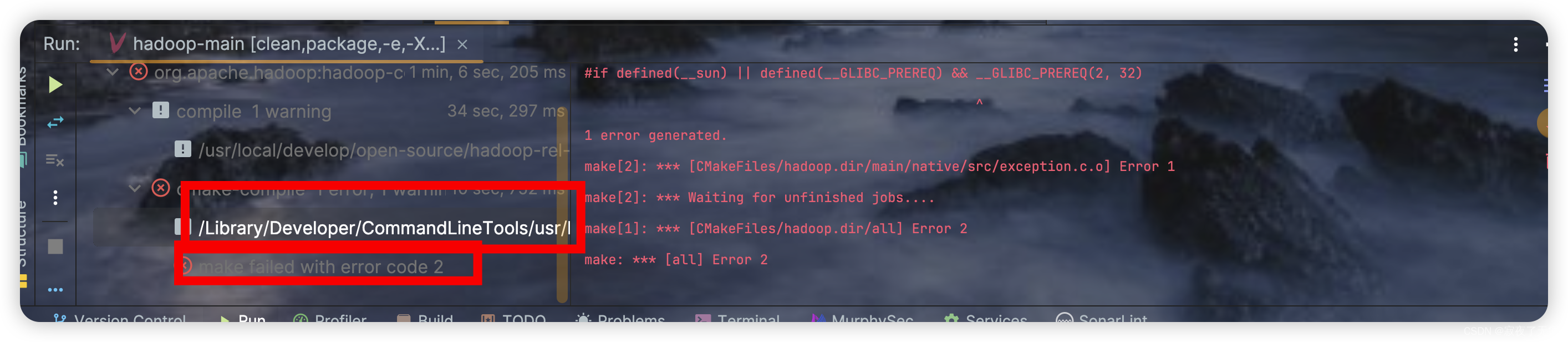
hadoop-common: CMake failed with error code 1
问题 在编译hadoop源码时遇到如下错误 hadoop-common: CMake failed with error code 1 看了这个错误表示一脸懵逼 排查 在mvn 的命令中增加 -X 和 -e mvn clean package -e -X -Pdist,native -DskipTests -Dmaven.javadoc.skip -Dopenssl.prefix/usr/local/bin/openssl 在…...

【面试】-科大讯飞日常实习面试
科大讯飞日常实习面试 提问的问题 面试30min,基本就是介绍项目以及提问java八股文,没有算法题 java保证线程安全的方法 需要根据具体场景选择合适的方法来保证线程安全。java中的异步请求如何实现你的SpringBoot项目怎么匹配在线人数请说出spring springMVC springboot之间的…...

MySQL 数据加密
MySQL 数据加密主要用于保护存储在数据库中的敏感信息,如用户密码、个人身份信息等。MySQL 提供了多种数据加密方法,主要包括: 对称加密: AES_ENCRYPT() 和 AES_DECRYPT() 函数:MySQL 支持使用高级加密标准(…...
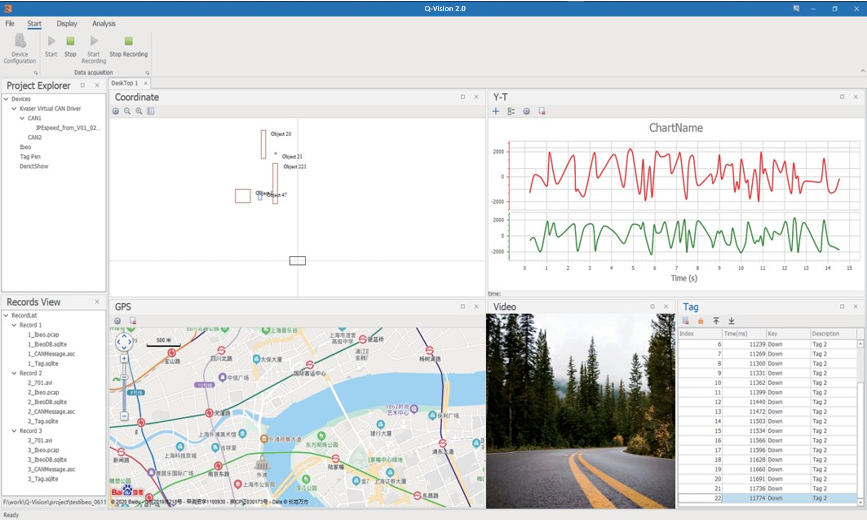
风丘科技为您提供完整的ADAS测试方案
一 方案概述 随着5G通讯与互联网的快速发展,智能汽车和ADAS辅助系统的研究与发展在世界范围内也在如火如荼地进行。风丘科技紧跟时代脚步,经多年积累沉淀,携手整车厂与高校共同研发打造出了一套完整且适用于国内ADAS测试的系统方案。 | ADAS…...
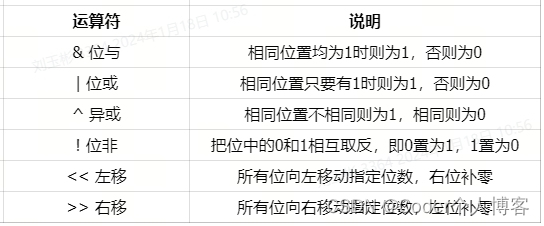
深入理解Rust基本类型
文章目录 一、概述二、数值类型2.1、整数类型2.2、浮点类型2.3、数字运算2.4、位运算2.5、序列(Range)2.6、有理数和复数 三、字符、布尔、单元类型3.1、字符类型3.2、布尔类型(bool)3.3、单元类型 团队博客: 汽车电子社区 一、概…...

cloudflare加速方法
一、使用Cloudflare优速域名或IP,实现国内访问加速 二、使用境外CN2、GIA等直连联网的VPS:如华纳云、彩红云等(未测试) 三、页面托管方案: 四、cloudflare合作伙伴计划:自定义cdn节点、dnspod提供的dns解析…...
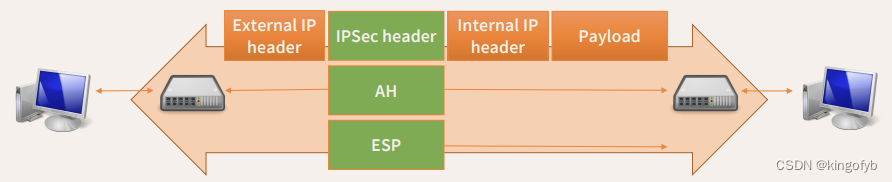
密码学学习笔记(二十四):TCP/IP协议栈
TCP/IP协议栈的基础结构包括应用层、传输层、网络层、数据链路层和物理层。 应用层 应用层位于TCP/IP协议栈的最顶层,是用户与网络通信的接口。这一层包括了各种高级应用协议,如HTTP(用于网页浏览)、FTP(用于文件传输…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
