游戏开发中的噪声算法
一、噪声
噪声是游戏编程的常见技术,广泛应用于地形生成,图形学等多方面。
那么为什么要引入噪声这个概念呢?在程序中,我们经常使用直接使用最简单的rand()生成随机值,但它的问题在于生成的随机值太“随机”了,得到的值往往总是参差不齐,如下图使用随机值作为像素点的黑白程度:
而使用噪声,我们得到的值看起来虽然随机但平缓,这种图也看起来更自然和舒服:
1.1 随机性
随机性是噪声的基础,不必多说。
1.2 哈希性
在《Minecraft》里,由于世界是无限大的,它以“Chunk”区块(16×16×256格子)为单位,只加载玩家附近的区块。也就是说,当玩家在移动时,它会卸载远离的区块,然后加载靠近的区块。
一个问题是,当玩家离开一个区块时,进入第二个区块,然后又回到第一个区块,此时玩家期望看到的第一个区块和之前看到的保持一致。例如,输入1时得到0.3,输入2时得到0.7,当再次输入1时预期得到0.3。
因此噪声的一个重要性质是哈希性(可哈希的)。
尽管使用输入值作为srand()的参数来设置rand()的种子,从而达到哈希效果也是可行的。
然而最好花点时间写一个自己的哈希函数,使其简易使用而且也不破坏程序其他地方使用rand()的效果。
//一个随机性的哈希函数
unsigned int hash11(int position){
const unsigned int BIT_NOISE1 = 0x85297A4D;
const unsigned int BIT_NOISE2 = 0x68E31DA4;
const unsigned int BIT_NOISE3 = 0x1B56C4E9;
unsigned int mangled = position;
mangled *= BIT_NOISE1;
mangled ^= (mangled >> 8);
mangled += BIT_NOISE2;
mangled ^= (mangled << 8);
mangled *= BIT_NOISE3;
mangled ^= (mangled >> 8);
return mangled;
}1.3 平滑性
对一个随机生成地形来说,如果简单的使用随机和哈希组合,
那么容易得到下图(以一维地图举例,x轴为位置,y轴为地形高度):
容易看出的问题是,由于随机的杂乱无章,地形非常的参差不齐,这可不是一个自然的地形。
我们期望得到的地形不仅随机还应该是平滑的,这样才显得自然,如下图:
为了达到连续性,自然想到利用插值函数进行插值,常见的插值方法有:线性插值、缓和曲线插值
二、Value噪声
Value噪声是最简单的一种噪声,其主要思路是定义若干个顶点且每个顶点含有一个随机值(以顶点坐标作为参数通过哈希运算得到的),该随机值会周围坐标产生影响,越靠近顶点则越容易受该顶点影响(输出值越接近顶点随机值)。当需要求某个坐标的输出值时,需要将该坐标附近的各个顶点所造成的影响值进行叠加,从而得到一个总值并输出之。
原理:
1.首先定义一个晶格结构,每个晶格的顶点有一个伪随机值(Value)。对于二维的Value噪声来说,晶格结构就是一个平面网格(通常是正方形),三维的就是一个立体网格(通常是正方体)。
2.输入一个点(二维空间的话就是2D坐标),我们找到它所在晶格的顶点(二维下有4个,三维下有8个,N维下有个),并经过哈希运算得到这些顶点的伪随机值。
3.根据这些顶点的伪随机值,使用插值函数计算出输入点的输出值。对于插值函数的权重,我们还需要使用缓和曲线(ease curves)来计算这些伪随机值的权重和。在原始的Perlin噪声实现所使用的缓和曲线是,在2002年的论文中Perlin又改进为
。

实现:
int valueNoise(Vector2 p){//晶格以1为长度单位,通过向下取整可以确定p点所在晶格//注意:不应使用转变整型,因为负数的转整型是向上取整,而正数则是向下取整,这可能会导致(-1~0)和(0~1)的边缘问题Vector2 pi = Vector2(floor(p.x),floor(p.y));//找到对应晶格的四个顶点坐标Vector2 vertex[4] = {{pi.x,pi.y},{pi.x+1,pi.y},{pi.x,pi.y+1},{pi.x+1,pi.y+1}};//通过hash21函数得出坐标对应的随机值float vertexRandom[4] = {{hash21(vertex[0])},{hash21(vertex[1])},{hash21(vertex[2])},{hash21(vertex[3])}}; //wx、wy代表p点的权重,实际就是以(0.0~1.0)的范围表示在晶格中的位置比例float wx = (p.x-pi.x))/1.0f;float wy = (p.y-pi.y))/1.0f;//插值return interpolation(wx,wy,vertexRandom);
}
三、柏林噪声
谈起噪声,最著名的且最常用的莫过于Perlin噪声,Perlin噪声的名字来源于它的创始人Ken Perlin。
在理解了上面Value噪声后,我们再来看看柏林噪声的主要想法:
定义若干个顶点且每个顶点含有一个随机梯度向量,这些顶点会根据自己的梯度向量对周围坐标产生势能影响,沿着顶点的梯度方向越上升则势能越高。当需要求某个坐标的输出值时,需要将该坐标附近的各个顶点所造成的势能进行叠加,从而得到一个总势能并输出之。

我们给顶点赋予一个随机性的哈希函数,输入一个坐标可以得到一个随机向量,满足上述随机性和哈希性。
此外,由于势能是沿着梯度方向渐变的,所以很容易得到平滑性。
原理:
和Value噪声一样,它也是一种基于晶格的噪声,也需要三个步骤:
1.首先定义一个晶格结构,每个晶格的顶点有一个随机的梯度向量。对于二维的Perlin噪声来说,晶格结构就是一个平面网格(通常是正方形),三维的就是一个立体网格(通常是正方体)
2.输入一个点(二维空间的话就是2D坐标),我们找到它所在晶格的顶点(二维下有4个,三维下有8个,N维下有个),并经过哈希运算得到这些顶点的梯度向量(随机向量);接着计算该点到各个晶格顶点的距离向量,再分别与顶点代表的梯度向量做点乘,得到
个梯度值结果
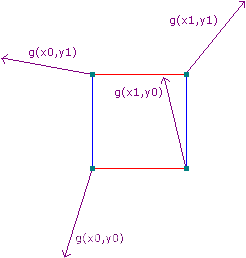
//点乘
float dot(Vector2 v1,Vector2 v2){return v1.x*v2.x+v1.y*v2.y;
}//求梯度值(本质是求顶点代表的梯度向量与距离向量的点积)
float grad(Vector2 vertex, Vector2 p)
{return dot(hash22(vertex), p);
}
3.使用缓和曲线来计算它们的权重和(同样的,可以是,也可以是
下图通过颜色差异显示了由2D柏林噪声生成的各像素点的值:

实现:
//二维柏林噪声
float perlinNoise(Vector2 p)
{ //向量两个纬度值向下取整Vector2 pi = Vector2(floor(p.x),floor(p.y));//找到对应晶格的四个顶点坐标Vector2 vertex[4] = {{pi.x,pi.y},{pi.x+1,pi.y},{pi.x,pi.y+1},{pi.x+1,pi.y+1}};//通过grad函数得出坐标对应的随机值float vertexRandom[4] = {grad(vertex[0],p),grad(vertex[1],p),grad(vertex[2],p),grad(vertex[3],p)}; //wx、wy代表p点的权重,实际就是以(0.0~1.0)的范围表示在晶格中的位置比例float wx = (p.x-pi.x))/1.0f;float wy = (p.y-pi.y))/1.0f;//插值return interpolation(wx,wy,vertexRandom);
}gard函数另一个更快的实现方式,它与标准实现方式的区别是:晶体顶点是从若干个梯度向量里随机选择一个向量而不是产生一个随机向量,这样做可以预先计算好求梯度值时各项的系数。因此我们只需这样重写一下grad函数:
//求梯度值(本质是求顶点代表的梯度向量与距离向量的点积)
float grad(Vector2 vertex, Vector2 p)
{switch(hash21(vertex) % 4){case 1: return p.x + p.y; //代表梯度向量(1,1)case 2: return -p.x + p.y; //代表梯度向量(-1,1)case 3: return p.x - p.y; //代表梯度向量(1,-1)case 4: return -p.x - p.y; //代表梯度向量(-1,-1)default: return 0; // never happens}
}
这里示例提供了4个可选的随机向量,实际上这个数量是偏少的,如果想要更加多样的效果,建议在实现时多提供些可选的随机向量。
四、Simplex噪声
Simplex噪声也是一种基于晶格的梯度噪声,它和Perlin噪声在实现上唯一不同的地方在于,它的晶格并不是方形(在2D下是正方形,在3D下是立方体,在更高纬度上我们称它们为超立方体,hypercube),而是单形(simplex)。
通俗解释单形的话,可以认为是在N维空间里,选出一个最简单最紧凑的多边形,让它可以平铺整个N维空间。我们可以很容易地想到一维空间下的单形是等长的线段,把这些线段收尾相连即可铺满整个一维空间。在二维空间下,单形是三角形,我们可以把等腰三角形连接起来铺满整个平面。三维空间下的单形就是四面体。更高维空间的单形也是存在的。
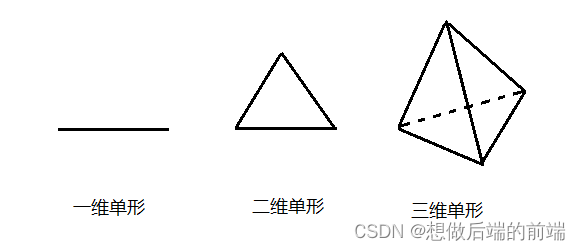
总结起来,在n维空间下,超立方体的顶点数目是,而单形的顶点数目是n+1,这使得我们在计算梯度噪声时可以大大减少需要计算的顶点权重数目。

一个潜在的问题是如何找到输入点所在的单形。
在计算Perlin噪声时,判断输入点所在的正方形是非常容易的,我们只需要对输入点下取整即可找到。
对于单形来说,我们需要对单形进行坐标偏斜(skewing),把平铺空间的单形变成一个新的网格结构,这个网格结构是由超立方体组成的,而每个超立方体又由一定数量的单形构成:

我们之前讲到的单形网格如上图中的红色网格所示,它们有一些等边三角形组成(注意到这些等边三角形是沿空间对角线排列的)。经过坐标倾斜后,它们变成了后面的黑色网格,这些网格由正方形组成,每个正方形是由之前两个等边三角形变形而来的三角形组成。这个把N维空间下的单形网格变形成新网格的公式如下:
其中,
在二维空间下,取n为2即可。这样变换之后,我们就可以按照之前方法判断该点所在的超立方体,在二维下即为正方形。
原理:
1.坐标偏斜:把输入点坐标进行坐标偏斜。
2.找到顶点:对偏斜后坐标下取整得到输入点所在的超立方体,...我们还可以得到小数部分
,...我们把之前得到的(xf,yf,...)中的数值按降序排序,来决定输入点位于变形后的哪个单形内。这个单形的顶点是由按序排列的(0, 0, …, 0)到(1, 1, …, 1)中的n+1个顶点组成,共有n!种可能性。
我们可以按下面的过程来得到这n+1个顶点:从零坐标(0, 0, …, 0)开始,找到当前最大的分量,在该分量位置加1,直至添加了所有分量。这一步的算法复杂度即为排序复杂度。
3.梯度选取:我们在偏斜后的超立方体网格上获取该单形的各个顶点的伪随机梯度向量。
4.变换回单形网格里的顶点:我们首先需要把单形顶点变回到之前由单形组成的单形网格。这一步需要使用第一步公式的逆函数来求得:
其中,
5.贡献度取和:我们由此可以得到输入点到这些单形顶点的位移向量。这些向量有两个用途,一个是为了和顶点梯度向量点乘,另一个是为了得到之前提到的距离值dist,来据此求得每个顶点对结果的贡献度:
实现:
float simplexNoise(Vector2 p)
{const float K1 = 0.366025404; // (sqrt(3)-1)/2;const float K2 = 0.211324865; // (3-sqrt(3))/6;//坐标偏斜float s = (p.X + p.Y) * K1;Vector2 pi = Vector2(floor(p.X+s),floor(p.Y+s));float t = (pi.X + pi.Y) *K2;Vector2 pf = p-(pi-t*Vector2::UnitVector);Vector2 vertex2Offset = (pf.X < pf.Y) ? Vector2(0, 1) : Vector2(1, 0);//顶点变换回单行网格空间Vector2 dist1 = pf;Vector2 dist2 = pf - vertex2Offset + K2 * Vector2::UnitVector;Vector2 dist3 = pf - Vector2(1,1) + 2 * K2 * Vector2::UnitVector;//计算贡献度取和float hx = 0.5f - Vector2::DotProduct(dist1, dist1);float hy = 0.5f - Vector2::DotProduct(dist2, dist2);float hz = 0.5f - Vector2::DotProduct(dist3, dist3);hx=hx*hx*hx*hx;hy=hy*hy*hy*hy;hz=hz*hz*hz*hz;//结果范围是[-1,1]return 70*(hx*Vector2::DotProduct(dist1, hash22(pi)) +hy*Vector2::DotProduct(dist2, hash22(pi + vertex2Offset))+hz*Vector2::DotProduct(dist3, hash22(pi + Vector2(1,1))));
}虽然理解上Simplex噪声相比于Perlin噪声更难理解,但由于它的效果更好、速度更优,因此很多情况下会替代Perlin噪声。
而且高维的噪声并不少见,例如对于常见的二维噪声纹理,我们可以额外引入时间分量,变成一个2D纹理动画(三维噪声),用于火焰纹理动画等..
对于常见的三维噪声纹理,引入额外的时间分量,就可以变成一个3D纹理动画(四维噪声),用于3D云雾动画等..
当我们需要一个可循环无缝衔接的动画时(见下文可平埔的噪声),那噪声又要提高一个维度。
相关文章:
游戏开发中的噪声算法
一、噪声 噪声是游戏编程的常见技术,广泛应用于地形生成,图形学等多方面。 那么为什么要引入噪声这个概念呢?在程序中,我们经常使用直接使用最简单的rand()生成随机值,但它的问题在于生成的随机值太“随机”了…...
CodeReview 小工具
大家开发中有没有遇到一个版本开发的非常杂,开发很多个项目,改动几周后甚至已经忘了自己改了些什么,领导要对代码review的时候,理不清楚自己改过的代码,只能将主要改动的大功能过一遍。这样就很容易造成review遗漏&…...
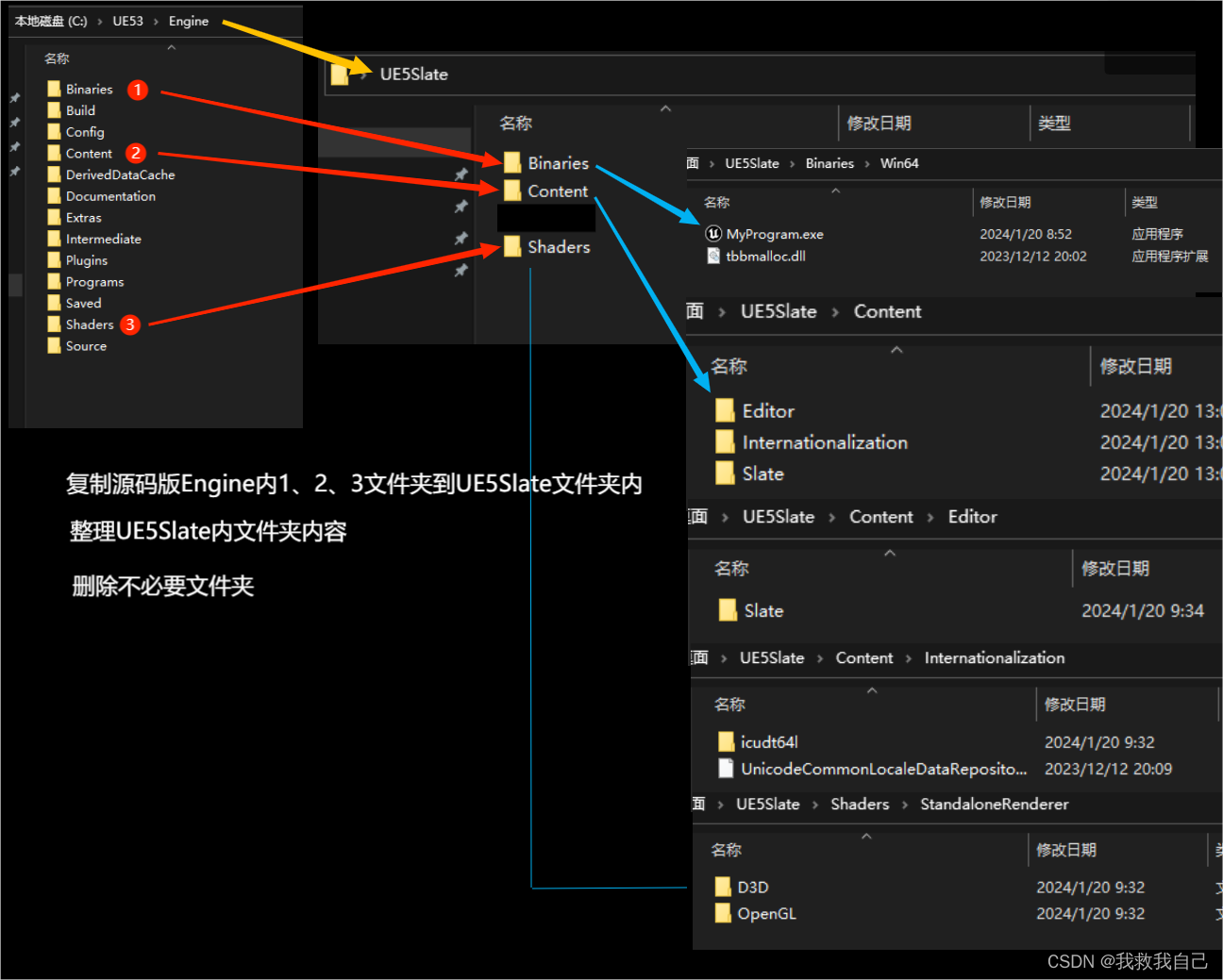
UE5 C++ Slate独立程序的打包方法
在源码版安装目录内找到已编译通过的xxx.exe,(\Engine\Binaries\Win64\xxx.exe),在需要的位置新建文件夹,拷贝源码版Engine内的Binaries、Content、Shaders文件夹到目标文件夹内,将xxx.exe放入对应位置,删除…...
探索设计模式的魅力:一篇文章让你彻底搞懂建造者模式
建造者模式(Builder Pattern)是一种创建型设计模式,旨在将一个复杂对象的创建过程与其表示分离,使得同样的构建过程可以创建不同的表示形式。 主要角色: 产品(Product):表示正在构建…...
Facebook广告投放指南,如何运营多个Facebook广告账户不被封?
许多卖家做广告投放会选择 Facebook 作为主要的业务和产品推广平台。然而,要在这个竞争激烈的平台上脱颖而出并成功拓宽广告覆盖面并不容易,通常情况下大家会运营多个Facebook广告账号,但是很多人因此遭遇Facebook账号被封的情况,…...
音乐人声分离工具:极简的人声和背景音乐分离工具
项目地址:jianchang512/vocal-separate: an extremely simple tool for separating vocals and background music, completely localized for web operation, using 2stems/4stems/5stems models 这是一个极简的人声和背景音乐分离工具,本地化网页操作&a…...
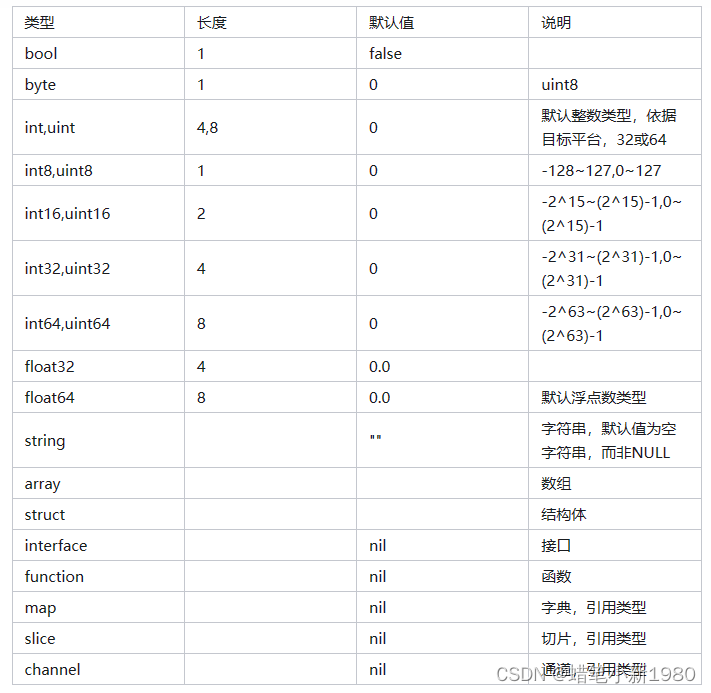
Go语言基础快速上手
1、Go语言关键字 2、Go数据类型 3、特殊的操作 3.1、iota关键字 Go中没有明确意思上的enum(枚举)定义,不过可以借用iota标识符实现一组自增常亮值来实现枚举类型。 const (a iota // 0b // 1c 100 // 100d // 100 (与上一…...
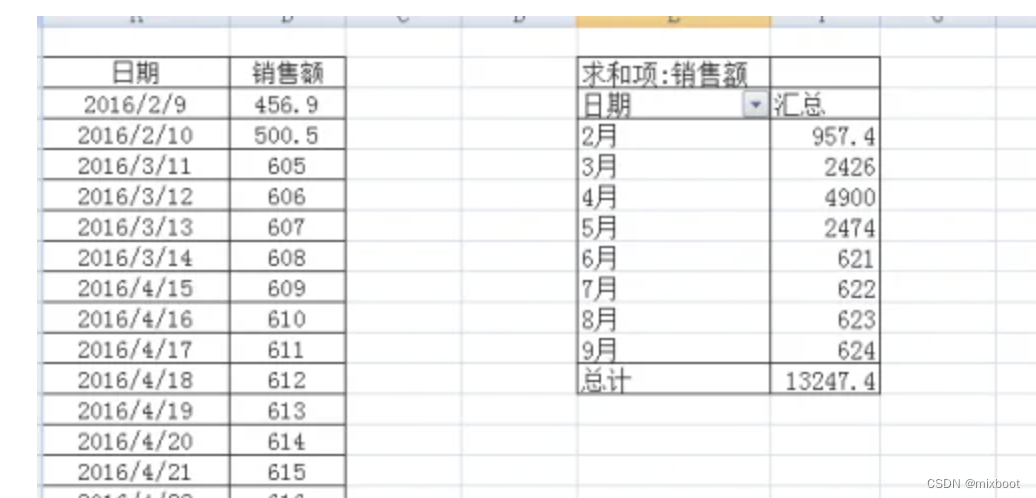
Excel 根据日期按月汇总公式
Excel 根据日期按月汇总公式 数据透视表日期那一列右击,选择“组合”,步长选择“月” 参考 Excel 根据日期按月汇总公式Excel如何按着日期来做每月求和...

使用 crypto-js 进行 AES 加解密操作
在前端开发中,数据的加密和解密是为了保障用户隐私和数据的安全性而常见的任务。AES(Advanced Encryption Standard)是一种对称密钥加密算法,被广泛用于保护敏感信息的传输和存储。本文将介绍 AES 加解密的基本原理,并…...
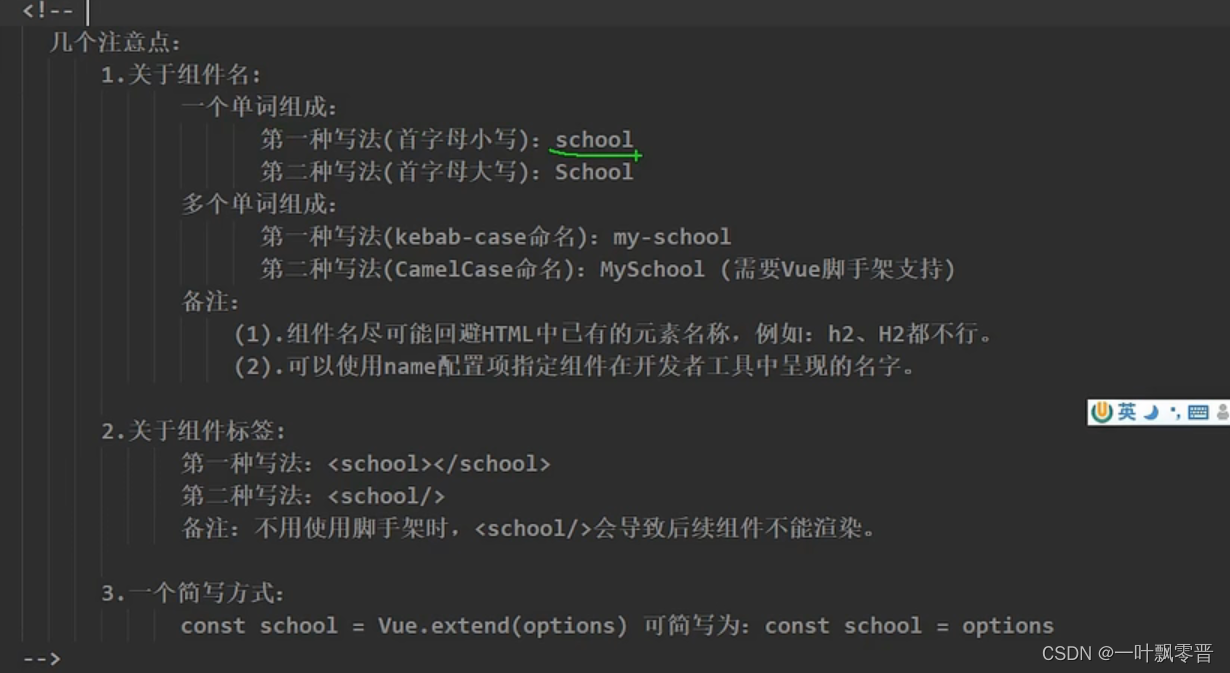
Vue-30、Vue非单文件组件。
非单文件组件: 一个组件包含n个组件 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>非单文件组件</title><script type"text/javascript" src"https://cdn.jsde…...

7-6 实验2_1_判断两数的大小
7-6 实验2_1_判断两数的大小 分数 100 全屏浏览题目 切换布局 作者 scs 单位 北京邮电大学 已知有两个整数,请使用if-else选择结构将它们中的较大数选择出来,存到max变量中;将较小数选择出来,存到min变量中,并将选…...

POKT Network (POKT) :进军百亿美元市场规模的人工智能推理市场
POKT Network(又称 Pocket Network)是一个去中心化的物理基础设施网络(DePIN),它能够协调并激励对任何开放数据源的访问,最初专注于向应用程序和服务提供商提供区块链数据。 自 2020 年主网上线以来&#x…...

【STM32】STM32学习笔记-I2C通信外设(34)
00. 目录 文章目录 00. 目录01. I2C简介02. I2C外设简介03. I2C框图04. I2C基本结构05. 主机发送06. 主机接收07. 软件/硬件波形对比08. 预留09. 附录 01. I2C简介 I2C(Inter-Integrated Circuit)总线是一种由NXP(原PHILIPS)公司开发的两线式…...
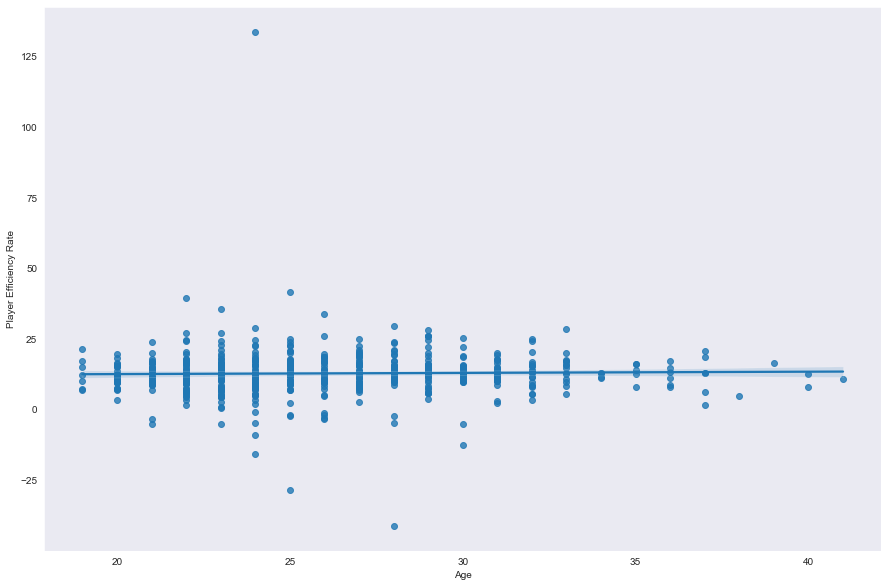
从数据角度分析年龄与NBA球员赛场表现的关系【数据分析项目分享】
好久不见朋友们,今天给大家分享一个我自己很感兴趣的话题分析——NBA球员表现跟年龄关系到底大不大?数据来源于Kaggle,感兴趣的朋友可以点赞评论留言,我会将数据同代码一起发送给你。 目录 NBA球员表现的探索性数据分析导入Python…...
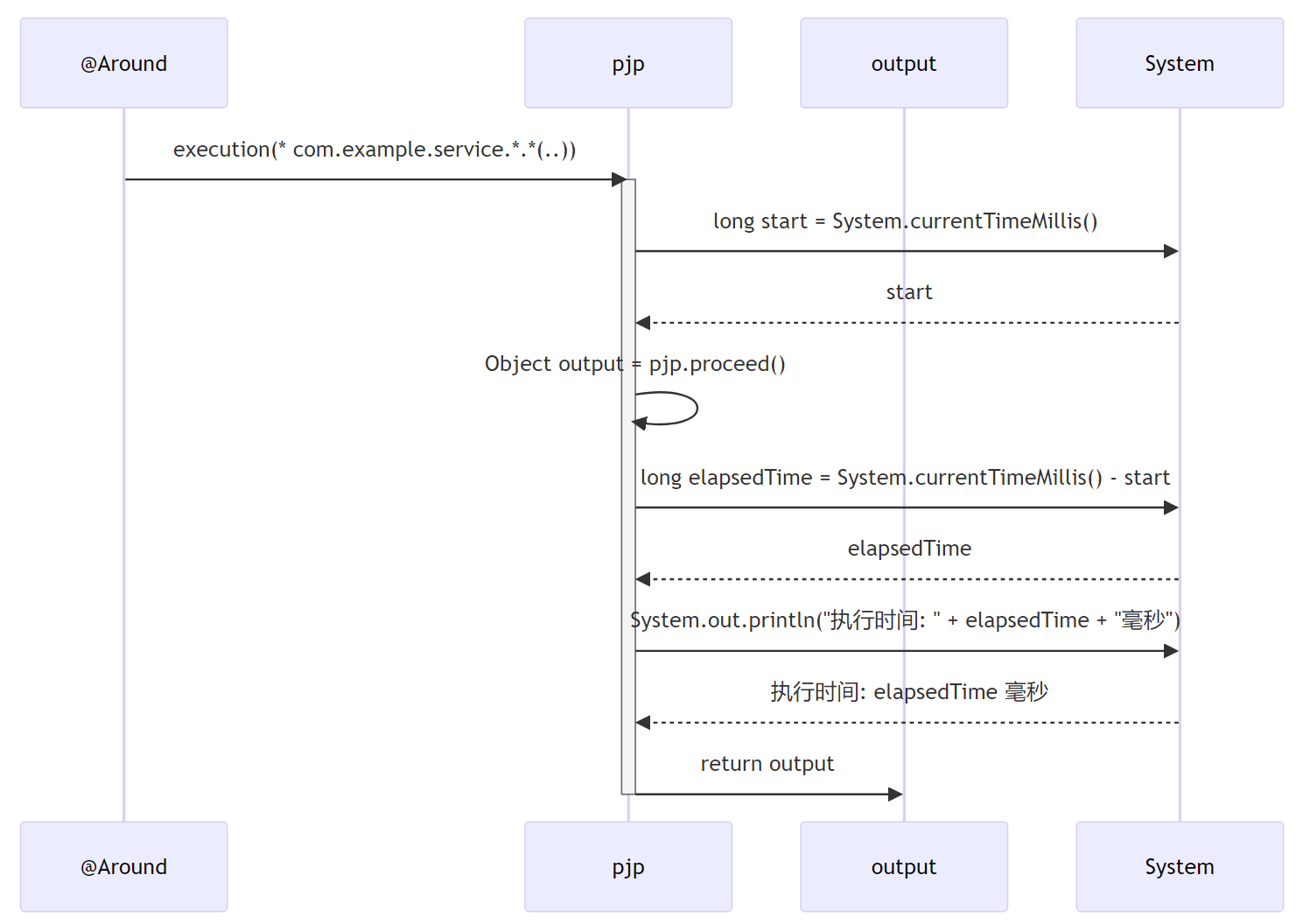
深入浅出Spring AOP
第1章:引言 大家好,我是小黑,咱们今天要聊的是Java中Spring框架的AOP(面向切面编程)。对于程序员来说,理解AOP对于掌握Spring框架来说是超级关键的。它像是魔法一样,能让咱们在不改变原有代码的…...

火速收藏!2024 新年微信红包封面领取全攻略
2024“龙”重登场!今年有哪些令人期待的红包封面? 前方大批精美红包封面来袭,全新品牌氛围红包封面上线,支持品牌定制特色氛围元素,沉浸感受浓浓年味儿,收获满满惊喜! 新年开好运,微…...

【RabbitMQ】RabbitMQ安装与使用详解以及Spring集成
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《RabbitMQ实战》。🎯🎯 &am…...

企业多云组网怎么办?
在当今数字化时代,企业普遍采用多云策略,同时利用不同云平台的优势以实现成本优化和整体性能提升。根据Futuriom于2022年发布的“安全多云网络调查”报告,80%的受访者表示他们使用来自两个或更多公共云提供商的PaaS或IaaS产品。 多云策略的迅…...
 二维01背包问题 Java)
背包问题(贪心) 二维01背包问题 Java
背包问题(贪心) 最优装载问题 题目描述 有n件物品和一个最大承重为w 的背包。第i件物品的重量是weight[i],每件只能用一次,求装入背包的最多物品数量。 题目分析 因为我们只要求装入物品的数量,所以装重的显然没有…...

2019年认证杯SPSSPRO杯数学建模D题(第二阶段)5G时代引发的道路规划革命全过程文档及程序
2019年认证杯SPSSPRO杯数学建模 D题 5G时代引发的道路规划革命 原题再现: 忙着回家或上班的司机们都知道交通堵塞既浪费时间又浪费燃料,甚至有的时候会带来情绪上的巨大影响,引发一系列的交通问题。据报道,每年交通拥堵使得美国…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
