Mysql深度分页优化的一个实践
问题简述:
最近在工作中遇到了大数据量的查询场景, 日产100w左右明细, 会查询近90天内的数据, 总数据量约1亿, 业务要求支持分页查询与导出.
无论是分页或导出都涉及到深度分页查询, mysql通过limit/offset实现的深度分页查询会存在全表扫描的问题, 比如offset=1000w, limit=10, 那么mysql会依次加载1000w条数据进行查找, 然后扔掉前1000w条, 然后返回找到的第1000w后的10条, 这种显然是傻瓜式的实现,显然会对内存和IO带来大量的消耗, 可想而知其耗时肯定会随着数据量的加大而上涨, 给个示例: 来源于[1]
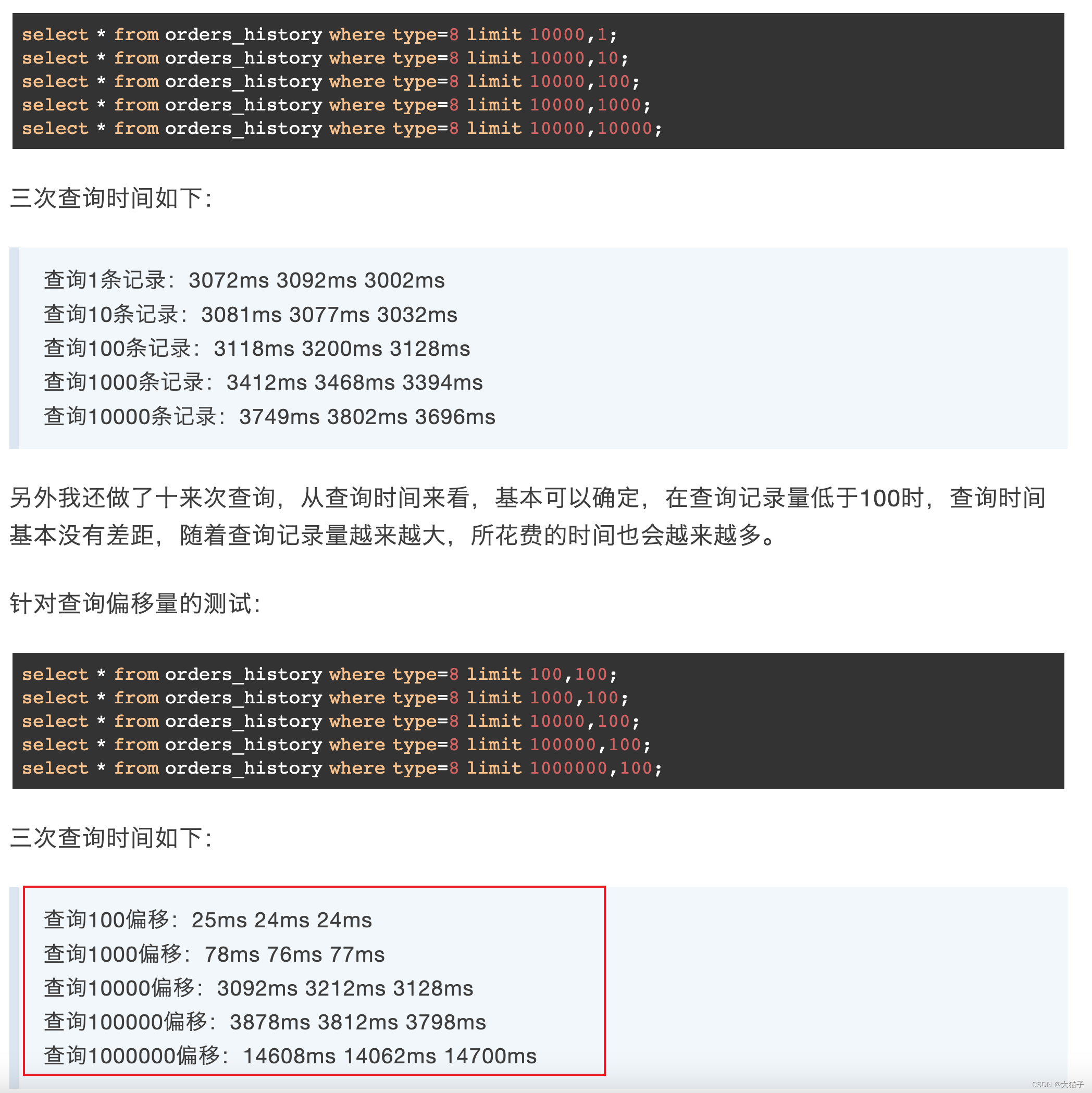
问题原因是mysql针对这种深度分页的近似全表扫描的操作导致: 参考[2]:
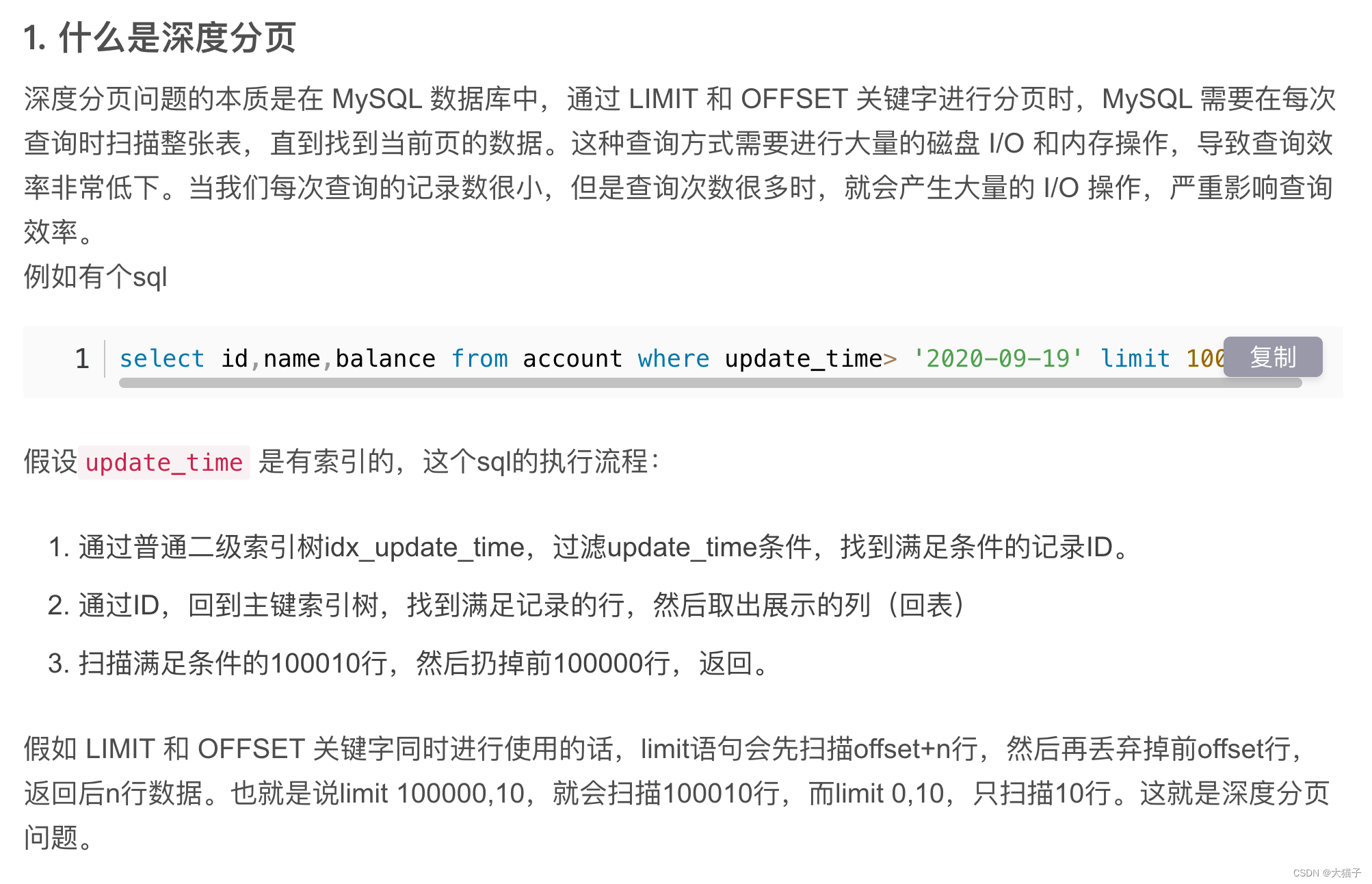
那么如何优化呢? 确保深度分页时耗时稳定, 与页码无关, 与数据量规模无关:
- 前端加一些限制: 限定不能任意跳转, 只能进行上一页与下一页的翻页操作, 业务能接受这种逻辑
- 后端针对翻页查询操作, 会记录上一次的id最大值与最小值, 在查询时通过标签过滤的方式过滤掉已翻页的数据, offset始终值为0
- 针对导出逻辑, 则很简单, 都无需考虑上一页, 一直下一页翻页处理即可.
这种处理也叫做标签记录法, 就是利用索引过滤来规避掉全表扫描问题的一种优化方式, 另外一种是子查询, 类似的操作, 只是即无需记录上次查询的结果, 每次查询时都重新查询下指定偏移量的最后一条记录, 将其ID作为过滤项或边界值, 然后进行查询, 本质是标签记录法, 换汤不换药
借用下[2]中的子查询的例子:
select id,name,balance FROM account where id >= (select a.id from account a where a.update_time >= '2020-09-19' limit 100000, 1) LIMIT 10;我觉得还是标签记录法性能时最好的, 一次查询解决. 就是要想办法维护下边界值, 尽量避免随机跳转.
另外近似深度分页的概念: 内存分页, 内存分页也是一种全表扫描的操作, 但是在应用层的过滤处理逻辑, 先获取全部数据, 然后在应用程序中对数据做处理, 数据量较小且sql逻辑复杂时会采取这种方式, sql中不建议加入太多代码逻辑, 调试与维护困难不说, 容易造成慢sql查询.
参考:
[1]:MySQL分页查询优化
[2]: MySQL深度分页-CSDN博客
相关文章:

Mysql深度分页优化的一个实践
问题简述: 最近在工作中遇到了大数据量的查询场景, 日产100w左右明细, 会查询近90天内的数据, 总数据量约1亿, 业务要求支持分页查询与导出. 无论是分页或导出都涉及到深度分页查询, mysql通过limit/offset实现的深度分页查询会存在全表扫描的问题, 比如offset1000w, limit10…...
【JavaEE进阶】 SpringBoot配置⽂件
文章目录 🍀配置⽂件的作⽤🌴SpringBoot配置⽂件🎋配置⽂件的格式🎄properties配置⽂件🚩properties基本语法🚩读取配置⽂件🚩properties的缺点 🌳yml配置⽂件yml基本语法Ƕ…...

excel 常用函数
求和函数: SUM: 将单个值、单元格引用或区域相加。 案例:SUM(A1:A5) (结果:A1到A5单元格的值求和) SUMIF: 对选中范围内符合指定条件的值求和。 案例:SUMIF(B1:B5, ">50&qu…...
【React基础】– JSX语法
文章目录 认识JSX为什么React选择了JSXJSX的使用 React事件绑定this的绑定问题事件参数传递 React条件渲染React列表渲染列表中的key JSX的本质createElement源码Babel官网查看直接编写jsx代码 虚拟DOM的创建过程jsx – 虚拟DOM – 真实DOM声明式编程 阶段案例练习 认识JSX ◼ …...
SpringBoot 项目中后端实现跨域的5种方式!!!
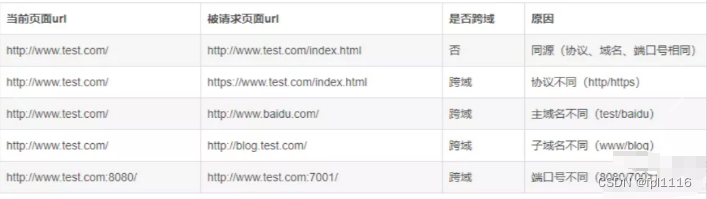
文章目录 SpringBoot 项目中后端实现跨域的5种方式!!!一、为什么会出现跨域问题二、什么是跨域三、非同源限制四、Java后端 实现 CORS 跨域请求的方式1、返回新的 CorsFilter(全局跨域)2、重写 WebMvcConfigurer(全局跨域)3、使用注解 (局部跨…...
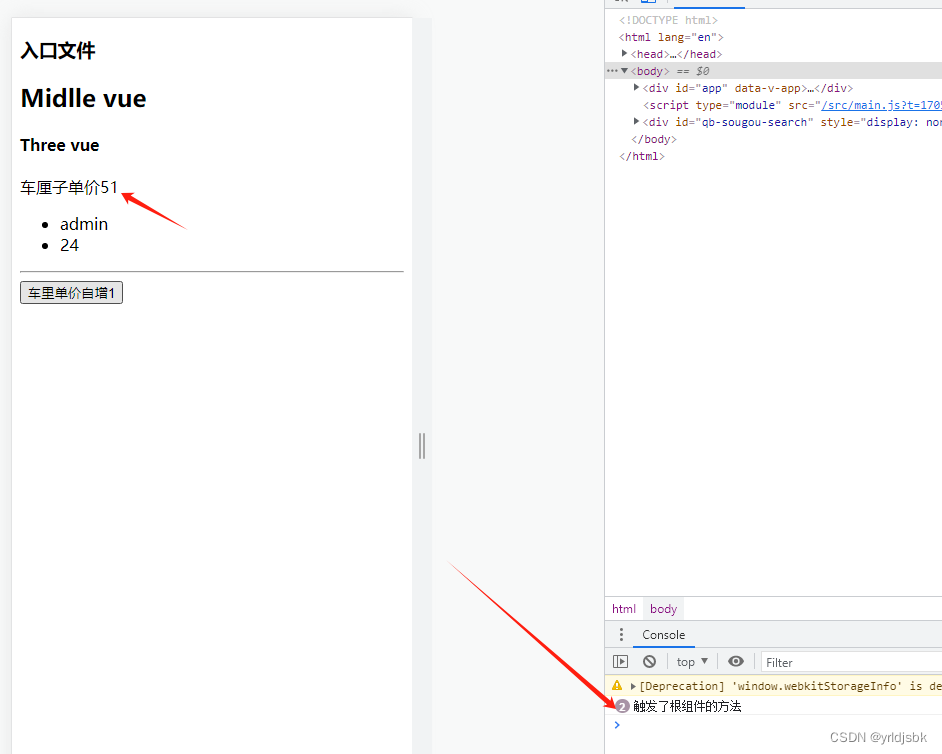
Vue3前端开发,provide和enject的基础练习,跨层级传递数据
Vue3前端开发,provide和enject的基础练习,跨层级传递数据! 声明:provide虽然可以跨层级传递,但是依旧是需要由上向下的方向传递。根传子的方向。 <script setup> import {onMounted, ref} from vue import Base from ./components/Base.vue impor…...

Python 循环结构值while循环
while循环是一种常用的循环结构,它会在满足特定条件的情况下重复执行一段代码块。 基本语法: while condition:# 循环体代码while循环的执行过程如下: 首先,判断循环条件condition(布尔表达式)是否为真。…...
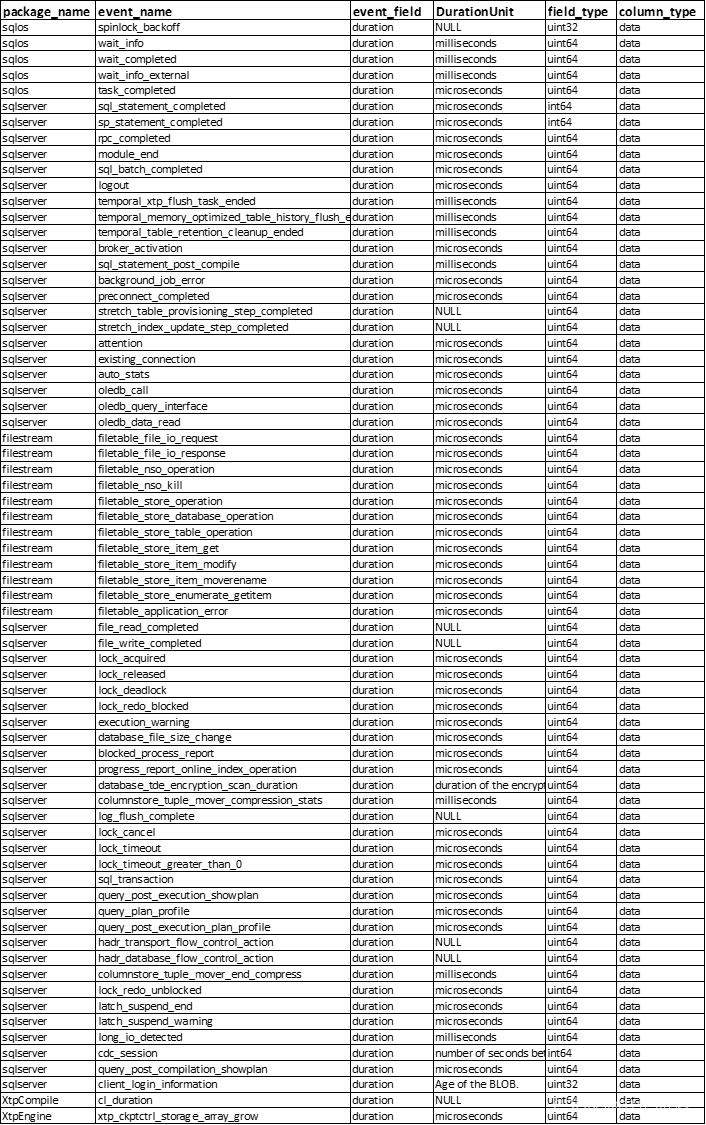
MSSQL-识别扩展extended event(扩展事件)中的时间单位
经常使用sqlserver extended event(扩展事件),但是总是忘记扩展事件使用的时间单位,不确定它们是 秒、毫秒、还是微秒? 以下下代码能够从 相关DMV中提取description字段内容来识别时间单位: SELECT [p].[name] [package_name],[o…...

vue3中l和vue2中v-model不同点
vue2比较让人诟病的一点就是提供了两种双向绑定:v-model和.sync, 在vue3中,去掉了.sync修饰符,只需要使用v-model进行双向绑定即可。 为了让v-model更好的针对多个属性进行双向绑定(vue2中自定义组件中v-model只能使用…...
使用 Swift 代码优化项目编译速度
引言 软件的性能是评价一个软件质量的重要指标,尤其在今天这个时代,性能已成为大型项目不可或缺的考虑因素之一。对于用户量极大的软件,如网银系统、在线购物商城等,更是必须保证其高效稳定的性能。在这种背景下,优化…...
基于springboot+vue的社区团购系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目背景…...
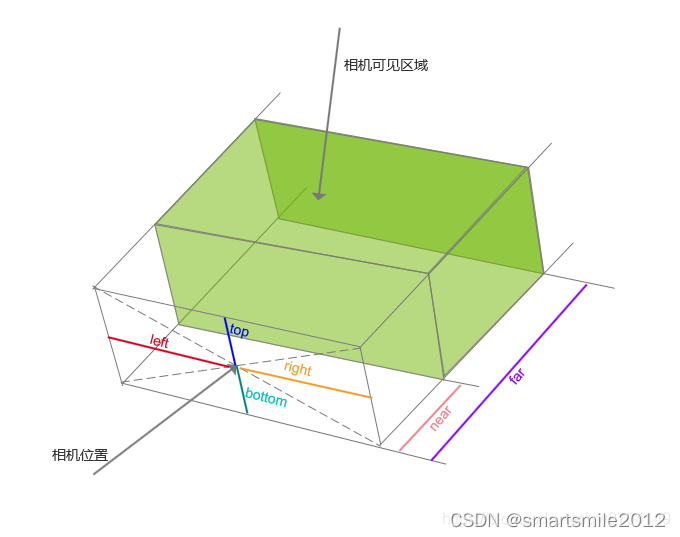
three.js从入门到精通系列教程002 - three.js正交相机OrthographicCamera
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title>three.js从入门到精通系列教程002 - three.js正交相机OrthographicCamera</title><script src"ThreeJS/three.js"></script><script src&qu…...
 - 性能、可用性)
Golang 搭建 WebSocket 应用(七) - 性能、可用性
在前面的文章中,提到过非功能性需求决定了架构。 今天我们再来考虑一下另外两个非功能性需求:性能和可用性。 前言 关于性能,其实并不是只有我们这个消息推送系统独有的问题。 对于所有的开发者而言,都多多少少会处理过性能相关…...
)
Qt 状态机框架:The State Machine Framework (一)
传送门: Qt 状态机框架:The State Machine Framework (一) Qt 状态机框架:The State Machine Framework (二) 一、什么是状态机框架 状态机框架提供了用于创建和执行状态图/表[1]的类。这些概念和表示法基于Harel的Statecharts:一种复杂系统的可视化形式,也是UML状态图的基…...

高通平台学习一
什么是QMI? Qualcom Message Interface 高通信息接口 高通平台目前都是非对称多核心,最主要的是AP和Modem。两个处理器怎么进行通信呢,我们把AP和Modem当作两个主机,问题就变得了很简单,TCP/IP协议不是一种非常成功的进程间跨主…...

Python爬虫时被封IP,该怎么解决?四大动态IP平台测评
在使用 Python 进行爬虫时,很有可能因为一些异常行为被封 IP,这主要是因为一些爬虫时产生的异常行为导致的。 在曾经的一次数据爬取的时候,我尝试去爬取Google地图上面的商家联系方式和地址信息做营销,可是很不幸,还只…...
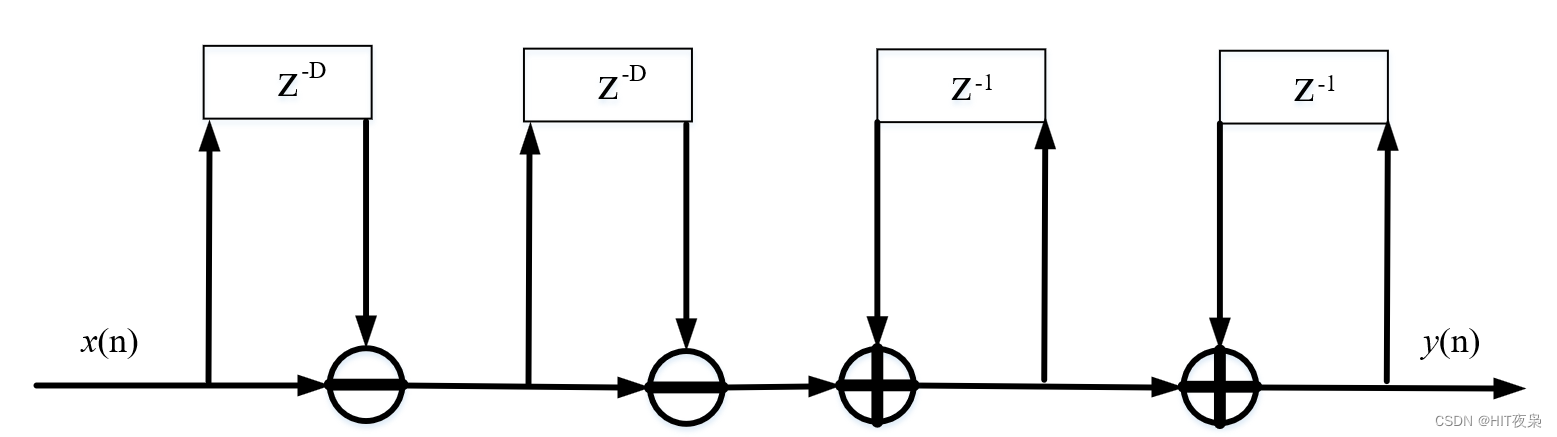
积分梳状滤波器CIC原理与实现
CIC(Cascade Intergrator Comb):级联积分梳状滤波器,是由积分器和梳状滤波器级联而得。滤波器系数为1,无需对系数进行存储,只有加法器、积分器和寄存器,资源消耗少,运算速率高&#…...
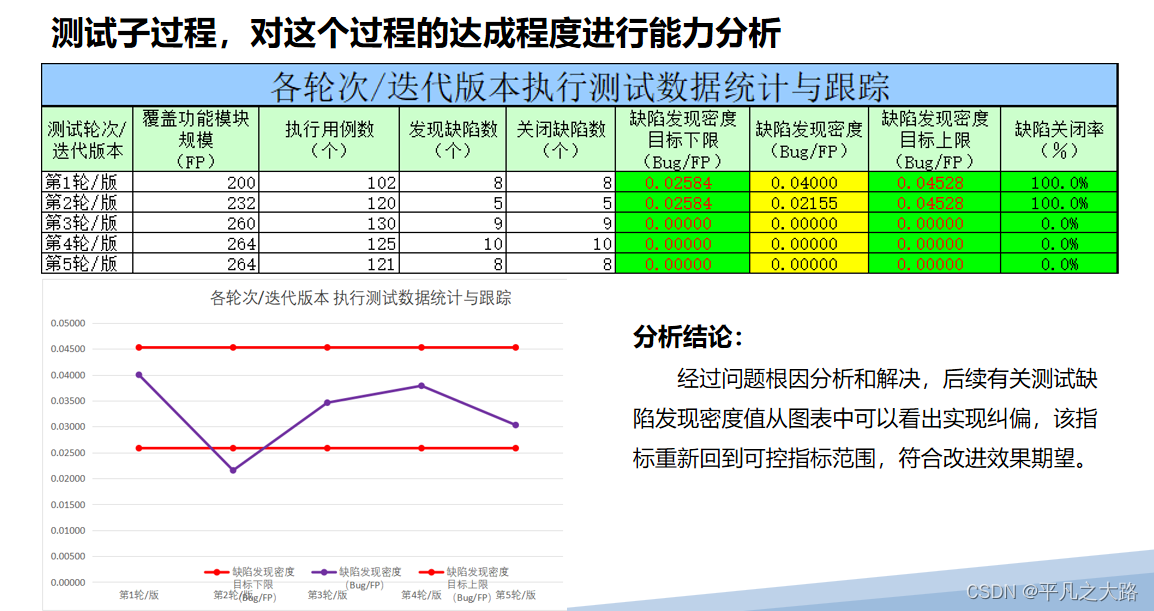
【项目管理】CMMI-原因分析与解决过程(CAR)
概述: “原因分析与解决”通过预防缺陷或者问题的引入以及识别并适当纳入优秀过程性能的原因,改进质量与生产率。 目录 1、文档结构 2、原因分析与解决过程域包括如下活动 3、选择需要加以分析的结果(启动条件) 4、过程活动与实践对照表 5、实例 1、…...
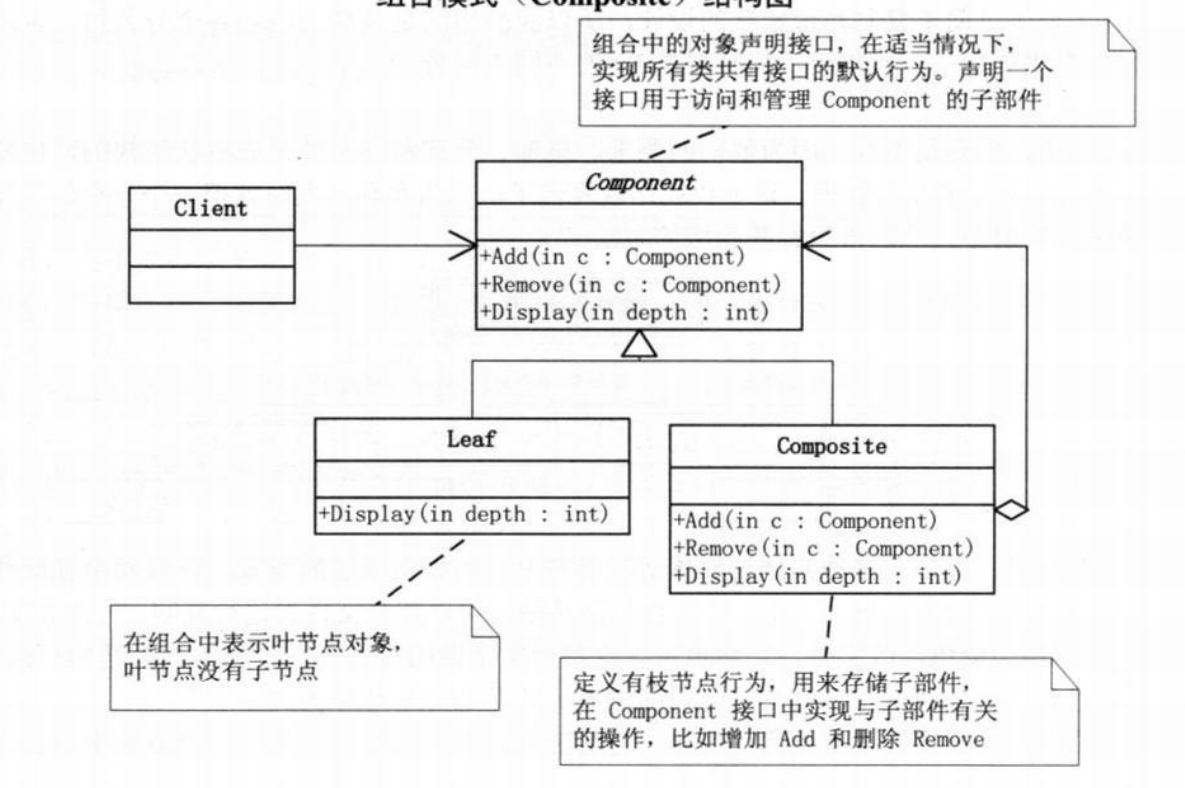
【设计模式】文件目录管理是组合模式吗?
组合模式是什么? 组合模式是一种将对象组合成树形结构以表示"部分-整体"的层次结构的设计模式。它使得用户对单个对象和组合对象的使用具有一致性。 组合模式在什么情况下使用? 当你发现你需要在代码中实现树形数据结构,让整体-部…...
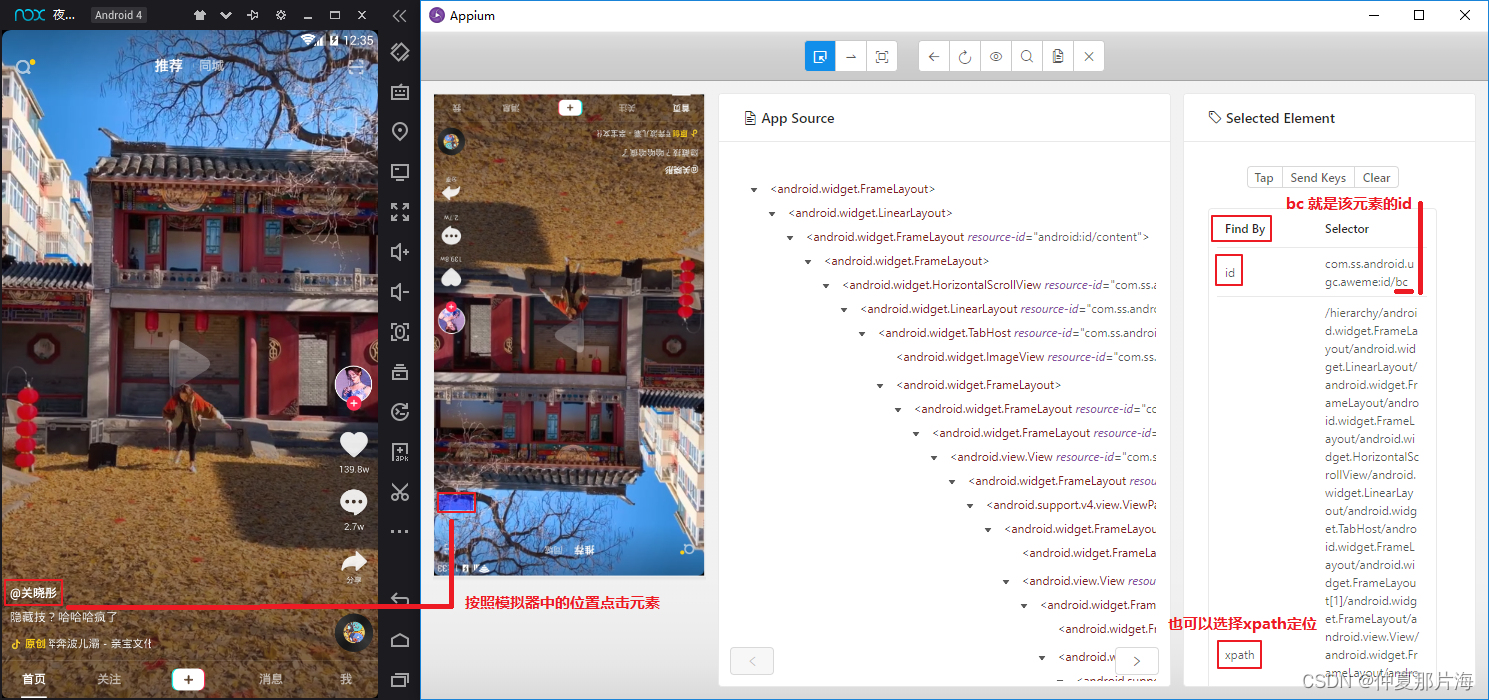
利用appium自动控制移动设备并提取数据
安装appium-python-client模块并启动已安装好的环境 安装appium-python-client模块 在window的虚拟环境下执行pip install appium-python-client 启动夜神模拟器,进入夜神模拟器所在的安装路径的bin目录下,进入cmd终端,使用adb命令建立adb…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
