深度学习常用代码总结(k-means, NMS)
目录
一、k-means 算法
二、NMS
一、k-means 算法
k-means 是一种无监督聚类算法,常用的聚类算法还有 DBSCAN。k-means 由于其原理简单,可解释强,实现方便,收敛速度快,在数据挖掘、数据分析、异常检测、模式识别、金融风控、数据科学、智能营销和数据运营等领域有着广泛的应用。具体实现步骤为:
- 设定 K 个类别的中心的初值;
- 计算每个样本到 K个中心的距离,按最近距离进行分类;
- 以每个类别中样本的均值,更新该类别的中心;
- 重复迭代以上步骤,直到达到终止条件(迭代次数、最小平方误差、簇中心点变化率)。
k-means 算法可以通过纯原生 python 语法实现,也可以通过 numpy 科学数据包实现。
纯原生 python 语法实现:
# 定义 List 求距离的函数
def getDistance(point1, point2, dim):sum = 0for i in range(dim):sum += (point1[i]-point2[i])**2return pow(sum, 0.5)# 定义 List 求和的函数,引用调用
def getSum(point1, point2, dim):for i in range(dim):point1[i] += point2[i]# 定义 List 求除法的函数,引用调用
def getDiv(point1, v, dim):for i in range(dim):point1[i] /= v# 定义 List 深拷贝的函数
def deepCopy(det1, det2):m, n = len(det1), len(det1[0])for i in range(m):for j in range(n):det1[i][j] = det2[i][j]# 定义主函数
def kmeans(dets, k, n):nums, dim = len(dets), len(dets[0])# 初始化旧的聚类中心,默认前kcenter_old = []for i in range(k):center_old.append(dets[i][:]) # [:]是浅拷贝 == copy()# 初始化新的聚类中心center_new = []for i in range(k):center_new.append([0]*dim)# 初始化一个记录的 Listcenter_num = [0]*dim# 迭代 n 次for _ in range(n):for i in range(nums):min_dis = 1e10min_idx = 0for j in range(k): # 基于最新距离找到第 i 数据的新的类别归属dis = getDistance(dets[i], center_old[j], dim)if min_dis > dis:min_dis = dismin_idx = jgetSum(center_new[min_idx], dets[i], dim) # 在新的类别归属上累计求和center_num[min_idx] += 1 # 记录数量,以求均值for i in range(k): # 求取均值,获得新的聚类中心getDiv(center_new[i], center_num[i], dim)deepCopy(center_old, center_new) # 将新的聚类中心赋值给旧的聚类中心for i in range(k): # 清空新的聚类中心for j in range(dim):center_new[i][j] = 0center_num[i] = 0return center_oldif __name__ == "__main__":x = [[1, 2], [1.5, 1.8], [5, 8], [8, 8], [1, 0.6], [9, 11]]y = kmeans(x, 2, 50)print(y) # 结果为:[[1.1667, 1.4666], [7.3333, 9.0]]numpy 科学数据包实现:参考
class Kmeans:def __init__(self, k=2, tolerance=0.01, max_iter=300):self.k = kself.tol = toleranceself.max_iter = max_iterself.features_count = -1self.classifications = Noneself.centroids = Nonedef fit(self, data):""":param data: numpy数组,约定shape为:(数据数量,数据维度):type data: numpy.ndarray"""self.features_count = data.shape[1]# 初始化聚类中心(维度:k个 * features种数)self.centroids = np.zeros([self.k, data.shape[1]])for i in range(self.k):self.centroids[i] = data[i]for i in range(self.max_iter):# 清空聚类列表self.classifications = [[] for i in range(self.k)]# 对每个点与聚类中心进行距离计算for feature_set in data:# 预测分类classification = self.predict(feature_set)# 加入类别self.classifications[classification].append(feature_set)# 记录前一次的结果prev_centroids = np.ndarray.copy(self.centroids)# 更新中心for classification in range(self.k):self.centroids[classification] = np.average(self.classifications[classification], axis=0)# 检测相邻两次中心的变化情况for c in range(self.k):if np.linalg.norm(prev_centroids[c] - self.centroids[c]) > self.tol:break# 如果都满足条件(上面循环没break),则返回else:returndef predict(self, data):# 距离distances = np.linalg.norm(data - self.centroids, axis=1)# 最小距离索引return distances.argmin()二、NMS
1. NMS
非极大值抑制 (Non-maximum supression) 简称 NMS,其作用是去除冗余的检测框,去冗余手段是剔除与极大值重叠较多的检测框结果。 通常我们所说的 NMS 指的是标准 NMS,非标准的 NMS 还有 soft NMS 和 softer NMS 参考 参考。那么为什么一定要去冗余呢?因为图像中的目标是多种多样的形状、大小和长宽比,目标检测算法中为了更好的保障目标的召回率,通常会使用 SelectiveSearch、RPN (例如:Faster-RCNN)、Anchor (例如:YOLO) 等方式生成长宽不同、数量较多的候选边界框 (BBOX)。因此在算法预测生成这些边界框后,紧接着需要跟着一个 NMS 后处理算法,进行去冗余操作,为每一个目标输出相对最佳的边界框,依次作为该目标最终检测结果。默认的两个框相似度的评判工具是 IOU,其它常用的还有 GIOU、DIOU、CIOU、EIOU 参考参考。
一般NMS后处理算法需要经历以下步骤(不含背景类,背景类无需NMS):
step1:先将所有的边界框按照类别进行区分;
step2:把每个类别中的边界框,按照置信度从高到低进行降序排列;
step3:选择某类别所有边界框中置信度最高的边界框bbox1,然后从该类别的所有边界框列表中将该置信度最高的边界框bbox1移除并同时添加到输出列表中;
step4:依次计算该bbox1和该类别边界框列表中剩余的bbox计算IOU;
step5:将IOU与NMS预设阈值Thre进行比较,若某bbox与bbox1的IOU大于Thre,即视为bbox1的“邻域”,则在该类别边界框列表中移除该bbox,即去除冗余边界框;
step6:重复step3~step5,直至该类别的所有边界框列表为空,此时即为完成了一个物体类别的遍历;
step7:重复step2~step6,依次完成所有物体类别的NMS后处理过程;
step8:输出列表即为想要输出的检测框,NMS流程结束。
import numpy as npdef IOU(point, points):# 计算交集面积lu = np.maximum(point[0:2], points[:, 0:2])rd = np.minimum(point[2:4], points[:, 2:4])intersection = np.maximum(0, rd-lu)inter_area = intersection[:,0]*intersection[:,1]# 计算每个框的单独面积area1 = (point[2]-point[0])*(point[3]-point[1])area2 = (points[:,2]-points[:,0])*(points[:,3]-points[:,1])union_area = np.maximum(area1+area2-inter_area, 1e-10)# 计算交并比return inter_area/union_areadef nms(dets, thresh):points = dets[:,:4]score = dets[:,4]order = score.argsort()[::-1]keep = []while order.size > 0:i = order[0]keep.append(i)ious = IOU(points[i,:], points[order[1:]]) # 当order.size==1时,order[1]会报错,但order[1:]不会报错inds = np.where(ious<=thresh)[0] # 对于IOU函数,order[1:]不会报错,但np.array([])则会报错order = order[inds+1] # 定义函数时,不需要特殊处理,numpy会自动帮忙处理这种情况return keepif __name__ == "__main__":dets = np.array([[30, 10, 200, 200, 0.95],[25, 15, 180, 220, 0.98],[35, 40, 190, 170, 0.96],[60, 60, 90, 90, 0.3],[20, 30, 40, 50, 0.1],])print(nms(dets, 0.5))2. soft-NMS
由于 NMS 直接删除所有 IOU 大于阈值的框,这种做法是粗暴的,有可能会漏检目标。因此,softe-nms 吸取了 NMS 的教训,在算法执行过程中不是简单的对 IOU 大于阈值的检测框删除,而是降低得分。soft-NMS 算法流程同 NMS 相同,但是对原置信度得分使用函数运算,目标是降低置信度得分。相比原 NMS 算法,只是将删除 IOU 过大框的操作修改为将 IOU 过大框的置信度降低。具体降低置信度的方法一般有两种,如下,分别是线性加权和高斯加权法。当所有 Box 都运算一遍后,将最终得分小于阈值的 Box 删除。
线性加权:

高斯加权:
![]()
import numpy as npdef soft_nms(boxes, thresh=0.3, sigma2=0.5, score_thresh=0.5, method=1):""":param boxes: 检测结果 n*5 前4列是x1y1x2y2, 第5列是置信度:param thresh: IOU阈值 :param sigma2: 高斯函数中用到的sigma:param score_thresh: 置信概率分数阈值:param method: soft-nms对应1或者2, 传统nms对应0:return: 最终保留的boxes的索引号"""# 初始化参数N = boxes.shape[0]indexs = [i for i in range(N)]# 得到每个box的左上角和右下角坐标并得到每个box的面积x1 = boxes[:, 0]y1 = boxes[:, 1]x2 = boxes[:, 2]y2 = boxes[:, 3]areas = (y2-y1+1)*(x2-x1+1)# 得到每个box的得分scores = boxes[:, 4]# 用keep存放保留的数据的索引并完成初始化,用keep_scores存放保留的数据的得分,该得分是乘以系数降低后的分数# 其实keep保存了所有得分非0的数据和得分,所有得分非0数据调整了数据的优先级进行排序,优先级逐步降低,最后再通过阈值去除一部分数据keep = []keep_scores = []pos = np.argmax(scores, axis=0)pos_scores = np.max(scores, axis=0)keep.append(pos)keep_scores.append(pos_scores)# 处理N-1次for _ in range(N):# 通过index-keep找到所有未检查的数据b = list(set(indexs).difference(set(keep)))# 计算当前pos数据与所有未检查数据的IOU# 计算交集的左上角和右下角x11 = np.maximum(x1[pos], x1[b])y11 = np.maximum(y1[pos], y1[b])x22 = np.minimum(x2[pos], x2[b])y22 = np.minimum(y2[pos], y2[b])# 如果两个方框相交, x22-x11, y22-y11是正的, 如果两个方框不相交,x22-x11, y22-y11是负的,将不相交的w和h设为0w = np.maximum(0, x22-x11)h = np.maximum(0, y22-y11)# 计算重叠交集的面积overlaps = w*h# 计算IOU, IOU公式(交集/并集)ious = overlaps / (areas[pos] + areas[b] - overlaps)# IOU大于阈值的重新赋值分数,大于阈值被认为是重叠度过高weight = np.ones(ious.shape)# Three methods: 1.linear 2.gaussian 3.original NMSif method == 1:weight[ious>thresh] = weight[ious>thresh] - ious[ious>thresh]elif method == 2:weight[ious>thresh] = np.exp(-(ious[ious>thresh])**2/sigma2)else:weight[ious>thresh] = 0scores[b] = weight*scores[b]# 更新pos, pos_scores, keep, keep_scoresb_scores = scores[b]if np.any(b_scores) == 0: # 如果全为0则不再继续循环breakpos = b[np.argmax(b_scores, axis=0)]pos_scores = np.max(b_scores, axis=0)keep.append(pos)keep_scores.append(pos_scores)# score约束keep = np.array(keep)keep_scores = np.array(keep_scores)indx = keep[keep_scores>=score_thresh]return indxif __name__ == "__main__":a = np.array([[191, 89, 413, 420, 0.80], # 0[281, 152, 573, 510, 0.99], # 1[446, 294, 614, 471, 0.65], # 2[50, 453, 183, 621, 0.98], # 3[109, 474, 209, 635, 0.78]]) # 4nms_result = soft_nms(a)print(a[nms_result])3. softer-NMS
以上两种 NMS 算法都忽略了一个问题,就是 NMS 时用到的 score 仅仅是分类置信度得分,不能反映 Bounding Box 的定位精准度,既分类置信度和定位置信非正相关的。因此, softer-NMS 改进了预测模型,原本预测模型输出为 4+1+nClass,其中 4 为 xywh,修改后的模型输出为 8+1+nClass,其中 8 为 x1_u、x1_std、y1_u、y1_std、x2_u、x2_std、y2_u、y2_std,这里用一个预测的高斯分布描述预测坐标的准确度。softer-NMS 的算法流程同 soft-NMS 相同。唯一的区别是在每次循环中,当排在首位的 Box 找到与其重叠度很高 (IOU 大于 thresh) 的一组 Box 后,除了基于 IOU 对这一组 Box 的 score 进行降低外,还需要基于这一组 Box 对排在首位的 Box 的坐标进行加权求平均,权重因子就是每个 Box 的坐标方差的倒数。在训练过程中,可以认为预测输出的 u 和 std 构成一个高斯分布,而真值 x 构成一个脉冲分布 (狄拉克 delta 分布),采用 KL 散度作为损失函数用于评价预测分布与真值分布之间的误差。
import numpy as npdef softer_nms(dets, confidence, thresh=0.6, score_thresh=0.7, sigma=0.5):""":param boxes: 检测结果 n*5 前4列是x1_u,y1_u,x2_u,y2_u, 第5列是置信度:param confidence: 检测结果 n*4 是x1_std,y1_std,x2_std,y2_std:param thresh: IOU阈值:param score_thresh: 置信概率分数阈值:param sigma: 高斯函数中用到的sigma:return: 最终保留的boxes"""# 初始化参数N = dets.shape[0]# 构建一个N*N的矩阵,第i-j表示第i个box与第j个box之间的IOU# 获取每个box的左上角和右下角坐标,直接=号是引用,后面会对dets做改变,所以这里需要浅拷贝x1 = dets[:, 0].copy()y1 = dets[:, 1].copy()x2 = dets[:, 2].copy()y2 = dets[:, 3].copy()# 计算每个box的面积,用于IOU的计算areas = (x2-x1)*(y2-y1)# 预定义IOU矩阵ious = np.zeros((N,N))# 循环计算IOU,这里存在重复计算,其实可以优化一下!!!for i in range(N):# 计算交集坐标xx1 = np.maximum(x1[i], x1)yy1 = np.maximum(y1[i], y1)xx2 = np.minimum(x2[i], x2)yy2 = np.minimum(y2[i], y2)# 计算交集宽高w = np.maximum(0.0, xx2-xx1)h = np.maximum(0.0, yy2-yy1)# 计算交集面积inter = w*h# 计算IOUious[i, :] = inter/(areas[i] + areas - inter)# 遍历循环N次,调整每个box的坐标(在IOU大于阈值的box中依照坐标方差加权求平均),以及按照优先级调整排序i = 0while i < N:# 找到i到n-1索引中的极大值索引,作为该轮循环中的待调整box,这里可以优化,如果最大值过小,就跳出循环!!!maxpos = dets[i:N, 4].argmax()maxpos += i# 对调第i和第maxpos的位置,让maxpos成为本轮循环的待调整box和最高优先级box,排位在最靠前位置,如此操作会比较耗时,可以优化为只对索引操作!!!dets[[maxpos, i]] = dets[[i, maxpos]]confidence[[maxpos, i]] = confidence[[i, maxpos]]areas[[maxpos, i]] = areas[[i, maxpos]]ious[[maxpos, i]] = ious[[i, maxpos]]ious[:,[maxpos, i]] = ious[:,[i, maxpos]]# 找到与待调整box的IOU大于阈值的box,利用这些box的坐标调整待调整box的坐标,1/confidence是加权参数ovr_bbox = np.where(ious[i,:N]>thresh)[0]avg_std_bbox = ((dets[ovr_bbox,:4] / confidence[ovr_bbox]).sum(0)) / ((1/confidence[ovr_bbox]).sum(0))dets[i, :4] = avg_std_bbox# 利用待调整box调整从i+1到N-1中与其重叠度过高的box的得分,与soft-nms一模一行,这里也可以优化为矩阵运算!!!pos = i + 1while pos < N:if ious[i , pos] > 0:# 得到IOU并利用高斯函数调整得分ovr = ious[i, pos]dets[pos, 4] *= np.exp(-(ovr*ovr)/sigma)# 如果得分过低,可以将其移到最后,这里其实有点浪费,即使没有这部分代码,经过N-1个循环后,最小得分的也都是在最后,可以优化!!!if dets[pos, 4] < score_thresh:dets[[pos, N-1]] = dets[[N-1, pos]]confidence[[pos, N-1]] = confidence[[N-1, pos]]areas[[pos, N-1]] = areas[[N-1, pos]]ious[[pos, N-1]] = ious[[N-1, pos]]ious[:,[pos, N-1]] = ious[:,[N-1, pos]]N -= 1 # 减少循环的次数pos -= 1pos += 1i += 1return dets[:N, :]if __name__ == "__main__":a = np.array([[191, 89, 413, 420, 0.80], # 0[281, 152, 573, 510, 0.99], # 1[446, 294, 614, 471, 0.65], # 2[50, 453, 183, 621, 0.98], # 3[109, 474, 209, 635, 0.78]]) # 4b = np.array([[1, 1, 1, 1], # 0[1, 1, 1, 1], # 1[1, 1, 1, 1], # 2[1, 1, 1, 1], # 3[1, 1, 1, 1]]) # 4nms_result = softer_nms(a, b)print(nms_result)相关文章:
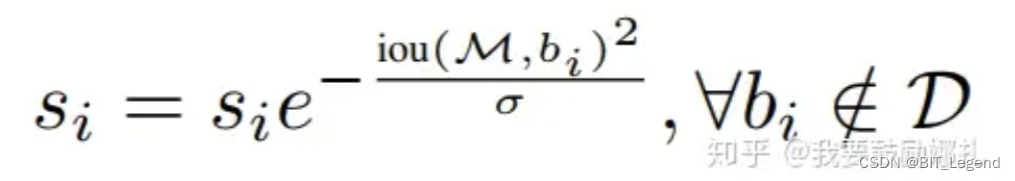
深度学习常用代码总结(k-means, NMS)
目录 一、k-means 算法 二、NMS 一、k-means 算法 k-means 是一种无监督聚类算法,常用的聚类算法还有 DBSCAN。k-means 由于其原理简单,可解释强,实现方便,收敛速度快,在数据挖掘、数据分析、异常检测、模式识别、金…...
数据结构·顺序表应用
本节应用是要用顺序表实现一个通讯录,收录联系人的姓名、性别、电话号码、住址、年龄 顺序表的实现在上一节中已经完成了,本节的任务其实就是应用上节写出来的代码的那些接口函数功能,做出来一个好看的,可…...

第一个 OpenGL 程序:旋转的立方体(VS2022 / MFC)
文章目录 OpenGL API开发环境在 MFC 中使用 OpenGL初始化 OpenGL绘制图形重置视口大小 创建 MFC 对话框项目添加 OpenGL 头文件和库文件初始化 OpenGL画一个正方形OpenGL 坐标系改变默认颜色 重置视口大小绘制立方体使用箭头按键旋转立方体深度测试添加纹理应用纹理换一个纹理 …...

剩余银饰的重量 - 华为OD统一考试
OD统一考试(C卷) 分值: 100分 题解: Java / Python / C 题目描述 有N块二手市场收集的银饰,每块银饰的重量都是正整数,收集到的银饰会被熔化用于打造新的饰品。 每一回合,从中选出三块 最重的…...
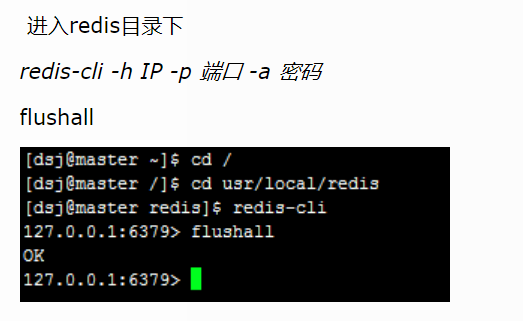
redis远程连接不上解决办法
问题描述: redis远程服务端运行在192.168.3.90计算机上,客户端计算机(ip:192.168.3.110)通过redsi-cli.exe客户端工具连接时,没有反应,连接不上。 如图所示: 解决步骤: 步骤一&…...
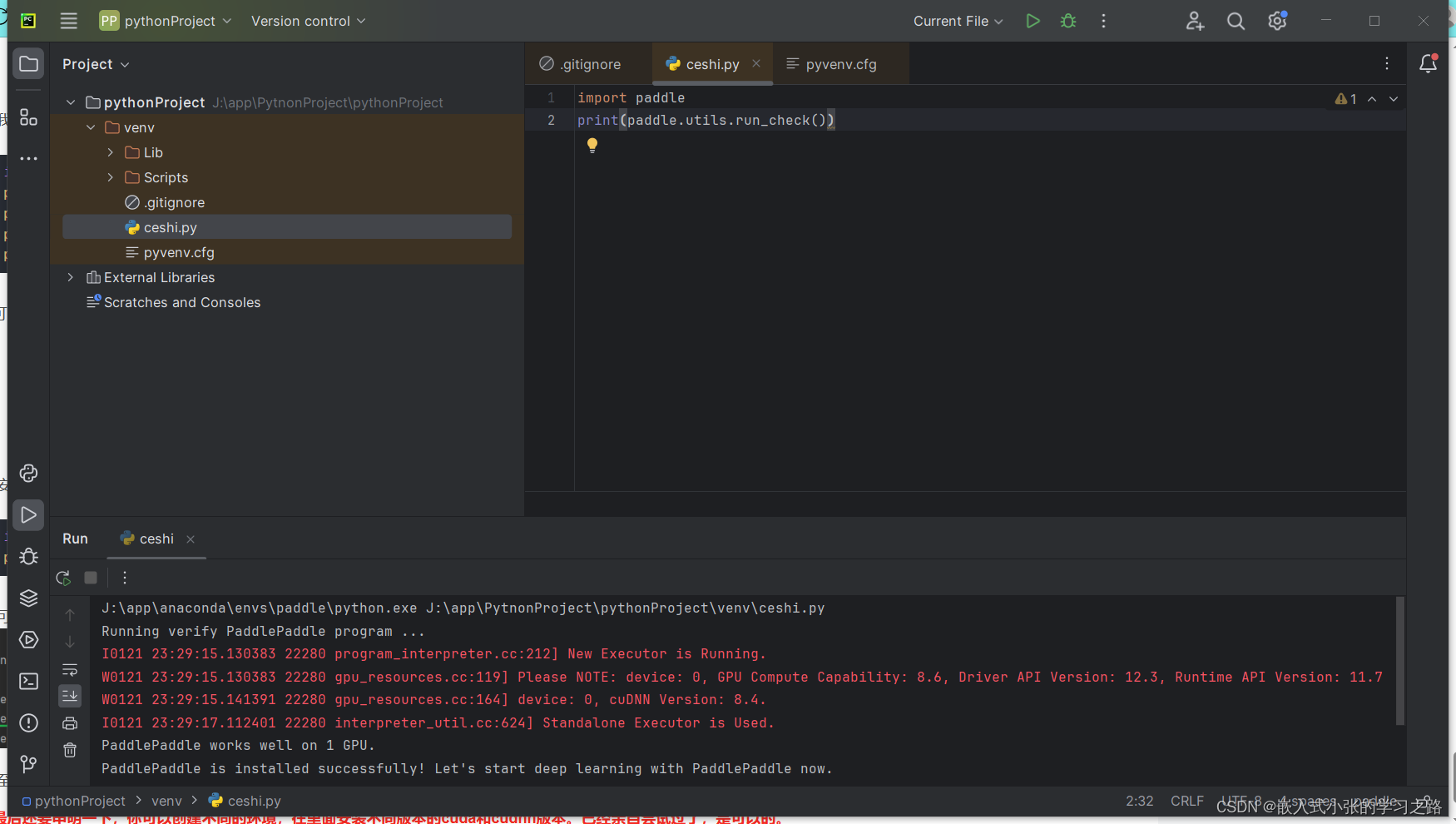
利用Anaconda安装pytorch和paddle深度学习环境+pycharm安装后不能调用pytorch和paddlepaddle框架
问题现象: 之前安装后不能在添加pytorch和paddlepaddle框架 原因(疑似): 在终端中显示pytorch和paddle在C盘但是安装是安装在J盘 解决办法: 卸载、删除文件重新安装后可以看到文件位置在J盘中 但是选择时还是显示C…...
Eclipses安装教程
一、下载开发工具包 1、开发工具包JDK 下载地址链接:https://www.oracle.com/cn/java/technologies/downloads/ 下载教程: 1)点击链接,可以跳转到页面 2)下滑页面,找到开发工具包 3) 记住下载之…...

安装python版opencv的一些问题
安装python版opencv的一些问题 OpenCV是知名的开源计算机视觉算法库,提供了C\Python\Java版共享库。 在Python中使用OpenCV格外简单,一句命令就能安装,一行import就能引入,可谓是神器。然而,在实际使用中可能遇到一些…...
RabbitMQ入门实战
RabbitMQ 是一个开源的消息中间件,实现了高级消息队列协议(AMQP),用于在分布式系统中进行消息传递。它能够在应用之间传递消息,解耦应用组件,提高系统的可伸缩性和可维护性。RabbitMQ 使用高级消息队列协议…...
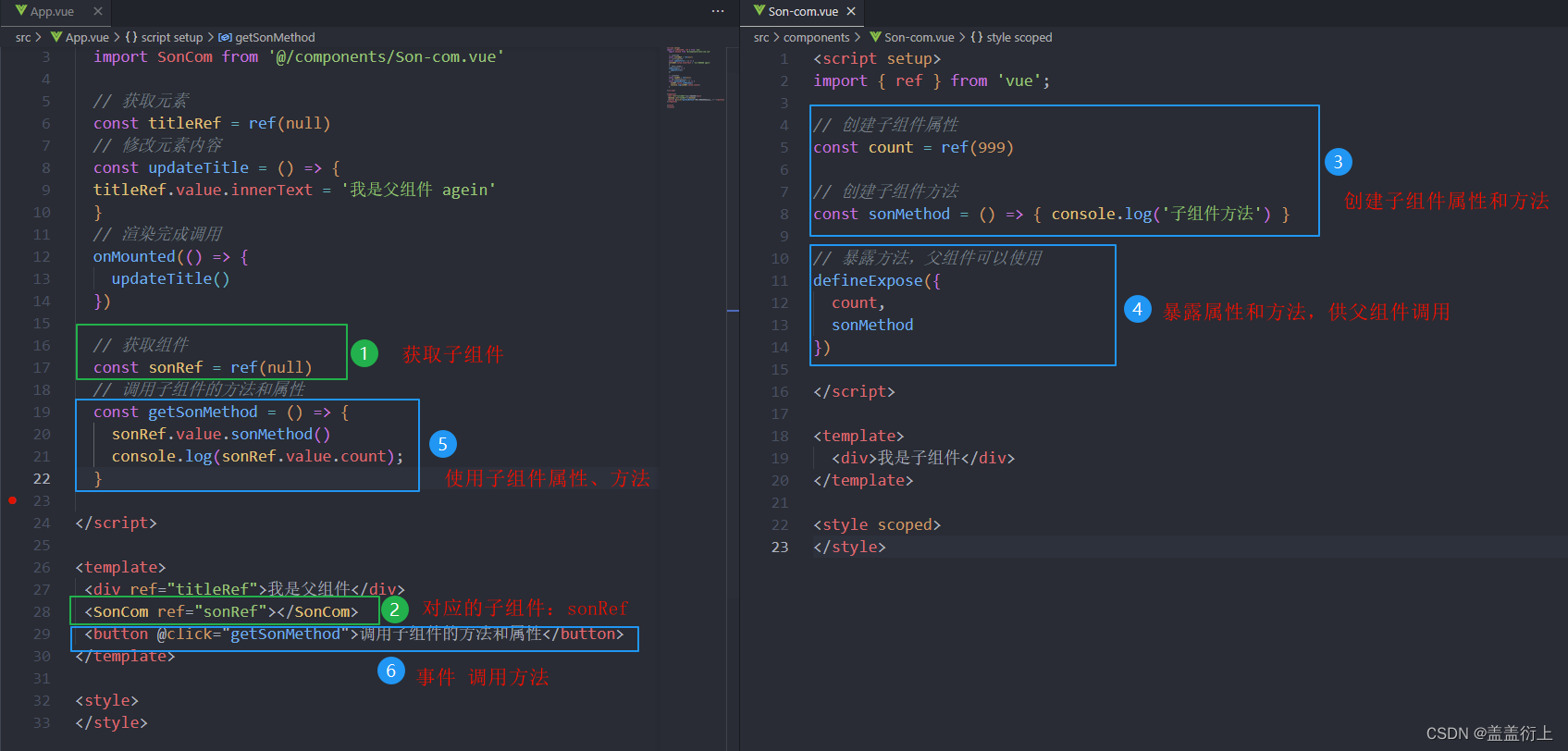
vue3-模版引用ref
1. 介绍 概念:通过 ref标识 获取真实的 dom对象或者组件实例对象 2. 基本使用 实现步骤: 调用ref函数生成一个ref对象 通过ref标识绑定ref对象到标签 代码如下: 父组件: <script setup> import { onMounted, ref } …...

C# 十大排序算法
以下是常见的十大排序算法(按照学习和实现的顺序排列): 冒泡排序(Bubble Sort)选择排序(Selection Sort)插入排序(Insertion Sort)希尔排序(Shell Sort&…...
面试之Glide如何绑定Activity的生命周期
Glide绑定Activity生命周期 Glide.with() 下面都是它的重载方法,Context,Activity,FragmentActivity, Fragment, android.app.Fragment fragment,View都可以作为他的参数,内容大同小异,都是先getRetriever࿰…...

从 fatal 错误到 sync.Map:Go中 Map 的并发策略
为什么 Go 语言在多个 goroutine 同时访问和修改同一个 map 时,会报出 fatal 错误而不是 panic?我们该如何应对 map 的数据竞争问题呢? 这篇文章将带你一步步了解背后的原理,并引出解决 map 并发问题的方案。 Map 数据竞争 首先…...

Simon算法详解
0.0 Intro 相关的算法: Deutsh-Jozsa算法: 第一个量子算法对经典算法取得指数级加速的算法 美中不足在于只能确定函数是平衡的还是非平衡的,无法确定函数具体的内容,即无法直接解出函数 Bernstein-Vazirani算法ÿ…...

jrebel IDEA 热部署
1 下载 2022.4.1 JRebel and XRebel - IntelliJ IDEs Plugin | Marketplace 2 选择下载好的zip 离线安装IDEA 插件 重启IDEA 3 打开 [Preference -> JRebel & XRebel] 菜单,输入 GUID address 为 https://jrebel.qekang.com/1e67ec1b-122f-4708-87d…...

pdf拆分成各个小pdf的方法
背景:由于某些缘故,一个大的pdf需要拆分成页数少的pdf,或者pdf需要去掉指定页,那么就有必要对pdf进行重新编辑,这里需要用到一个库,直接进行操作即可。 当使用Python时,可以使用PyMuPDF库来拆分PDF文件。以下是一个示例代码, import fitz # PyMuPDF def split_pdf(i…...

IntelliJ IDEA 常用快捷键一览表(通用型,提高编写速度,类结构、查找和查看源码,替换与关闭,调整格式)
文章目录 IntelliJ IDEA 常用快捷键一览表1-IDEA的日常快捷键第1组:通用型第2组:提高编写速度(上)第3组:提高编写速度(下)第4组:类结构、查找和查看源码第5组:查找、替换…...
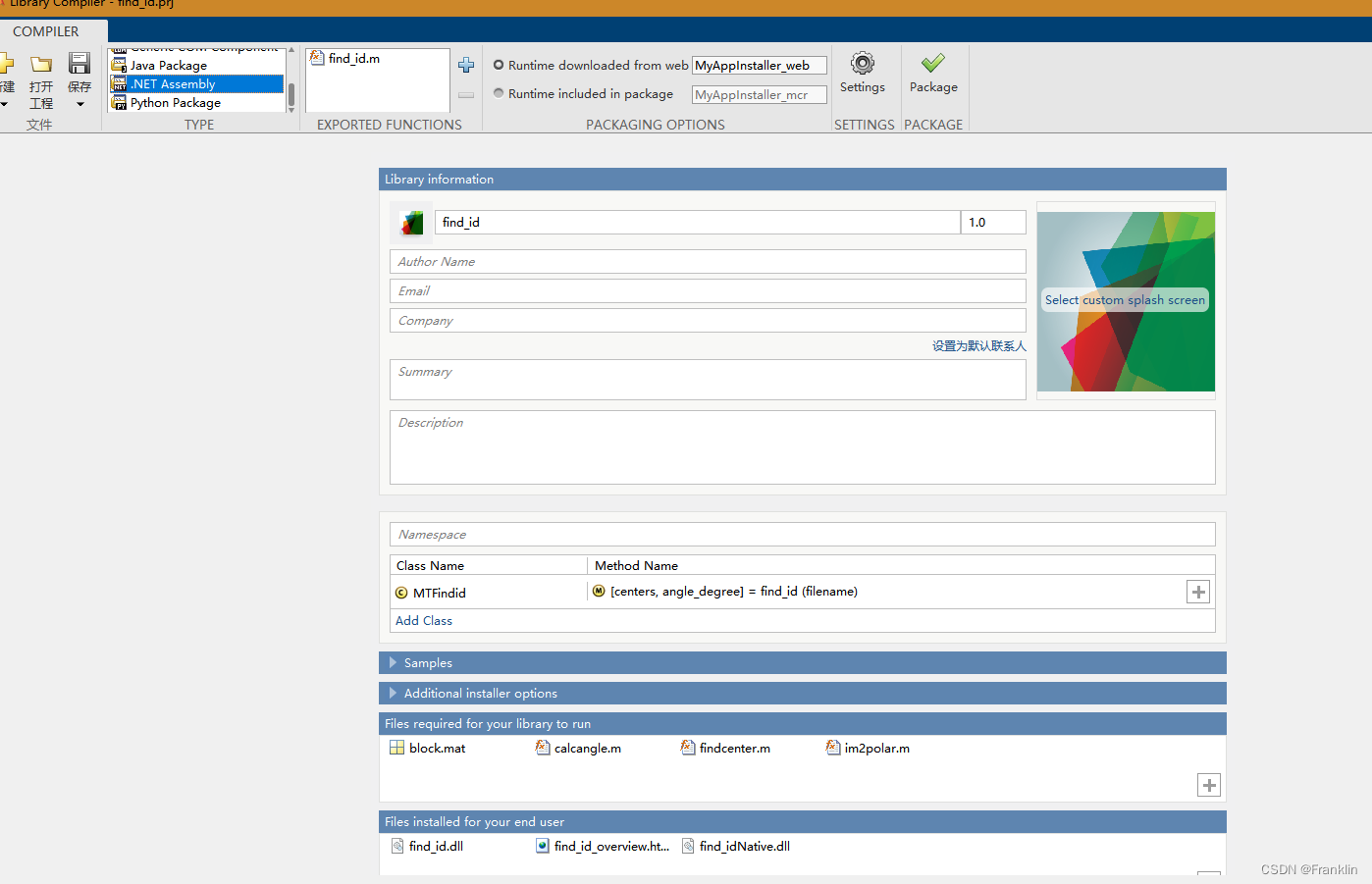
MSVS C# Matlab的混合编程系列2 - 构建一个复杂(含多个M文件)的动态库:
前言: 本节我们尝试将一个有很多函数和文件的Matlab算法文件集成到C#的项目里面。 本文缩语: MT = Matlab 问题提出: 1 我们有一个比较复杂的Matlab文件: 这个MATLAB的算法,写了很多的算法函数在其他的M文件里面,这样,前面博客的方法就不够用了。会报错: 解决办法如下…...

上位机图像处理和嵌入式模块部署(qt图像处理)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 很多人一想到图像处理,本能的第一反应就是opencv,这也没有错。但是呢,这里面还是有一个问题的,不知…...

AI教我学编程之C#类的实例化与访问修饰符
前言 在这篇文章中,我将带大家深入了解C#编程语言的核心概念,包括类的实例化、访问修饰符的应用,以及C#中不同数据类型的默认值。我会通过逐步分析和具体实例,详细解释如何在C#中正确创建和操作对象,并探讨如何通过访…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
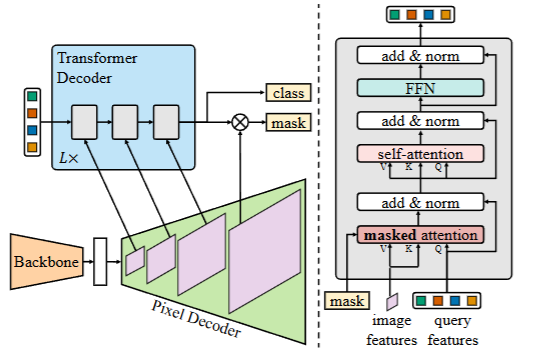
2025-06-08-深度学习网络介绍(语义分割,实例分割,目标检测)
深度学习网络介绍(语义分割,实例分割,目标检测) 前言 在开始这篇文章之前,我们得首先弄明白,什么是图像分割? 我们知道一个图像只不过是许多像素的集合。图像分割分类是对图像中属于特定类别的像素进行分类的过程,即像素级别的…...

基于微信小程序的作业管理系统源码数据库文档
作业管理系统 摘 要 随着社会的发展,社会的方方面面都在利用信息化时代的优势。互联网的优势和普及使得各种系统的开发成为必需。 本文以实际运用为开发背景,运用软件工程原理和开发方法,它主要是采用java语言技术和微信小程序来完成对系统的…...
