Simon算法详解
0.0 Intro
相关的算法:
Deutsh-Jozsa算法:
第一个量子算法对经典算法取得指数级加速的算法
美中不足在于只能确定函数是平衡的还是非平衡的,无法确定函数具体的内容,即无法直接解出函数
Bernstein-Vazirani算法:
在Deutsh-Jozsa算法基础上进一步提出,能够直接解出算法本身
同样存在问题,即没有实现指数级的加速
Simon算法 在上述两个算法的基础上更进一步,体现在两个方面
一方面,Simon算法可以在Simon问题中,直接解出目标函数
另一方面,Simon问题的经典解法是指数级复杂度,而Simon算法相较经典算法也是取得了指数级的加速。
1.1 Simon问题(Simon’s Problem)
现有一未知数,其作用域和值域都是n位的二进制数据: f : { 0 , 1 } n → { 0 , 1 } n f:\left \{ 0,1\right \}^{n} \to \left \{ 0,1\right \}^{n} f:{0,1}n→{0,1}n
该函数是单射或对称函数中的一种。当函数为对称时,有: x 1 + x 2 = s , f ( x 1 ) = f ( x 2 ) x_{1}+ x_{2}=s,f(x_{1})=f(x_{2}) x1+x2=s,f(x1)=f(x2)现需确定函数的属性,若属于对称函数需进一步确定 s
小贴士:
- 单射函数即作用域上每一个输入都有唯一输出的函数,常见的有实数域上所有的线性函数,例如f(x)=x、f(x)=lnx等都是单射函数
- 对称函数的性质在上面已经说明,其中s其实是x1和x2的对称轴,常见的对称函数即二次函数,例如f(x)=x^2,其对称轴s=0
1.2 Simon问题分析与经典解法的思路
1.2.1 Simon问题分析
需要注意的是,Simon问题中提到的值域和作用域始终都是n位二进制数,进行的加法严格意义上说是模二加法, 在模二加法中两个二进制数相加为0即表示这两个二进制数是相等的,因此可对Simon问题进行如下简化:
- 对于单射函数,显然有:在x1=x2时, x 1 + x 2 = 0 , f ( x 1 ) = f ( x 2 ) x_{1}+ x_{2}=0,f(x_{1})=f(x_{2}) x1+x2=0,f(x1)=f(x2)因此,s=0即为在单射函数情况下的解
- 对于对称函数,除了s=0这一个解之外,显然还有另一个非平凡解,即为对称函数对称轴的位置
小贴士
- 平凡解就是显而易见的解、没有讨论的必要但是为了结果的完整性仍需要考虑的结果,比如Ax=0中的零解,即x=0,即为平凡解
- 非平凡解(nontrivial solution)是齐次方程或齐次方程组的非零解。
1.2.2 Simon问题的经典解法(暴力解法)
可以通过将作用域取值不断带入进行验证的方法进行求解,考虑到单射函数与对称函数的区别,不必将整个作用域带入,只需要带入作用域的一半+1次即可完成验证。
作用域是n位二进制数,因此需要进行验证的次数为: 2 n − 1 + 1 2^{n-1}+1 2n−1+1
这里解释一下验证一半作用域后额外再验证一次的原因。最坏的情况下,验证一半作用域后会发现每一个输出都是唯一的,那么就需要额外再进行一次,将额外的一次结果与前面一半作用域产生的值进行比对:
- 如果仍然是新的唯一输出,则表明这是一个单射函数;
- 如果能与之前某个输出值匹配,则表明这是一个对称函数,该输出对应的输入值和这额外的一次输入值就可以确定对称轴的位置。
因而,Simon问题经典解法的时间复杂度是 O ( 2 n ) O(2^n) O(2n)
2.1 Simon算法详解
2024.1.15 待续…
相关文章:

Simon算法详解
0.0 Intro 相关的算法: Deutsh-Jozsa算法: 第一个量子算法对经典算法取得指数级加速的算法 美中不足在于只能确定函数是平衡的还是非平衡的,无法确定函数具体的内容,即无法直接解出函数 Bernstein-Vazirani算法ÿ…...

jrebel IDEA 热部署
1 下载 2022.4.1 JRebel and XRebel - IntelliJ IDEs Plugin | Marketplace 2 选择下载好的zip 离线安装IDEA 插件 重启IDEA 3 打开 [Preference -> JRebel & XRebel] 菜单,输入 GUID address 为 https://jrebel.qekang.com/1e67ec1b-122f-4708-87d…...

pdf拆分成各个小pdf的方法
背景:由于某些缘故,一个大的pdf需要拆分成页数少的pdf,或者pdf需要去掉指定页,那么就有必要对pdf进行重新编辑,这里需要用到一个库,直接进行操作即可。 当使用Python时,可以使用PyMuPDF库来拆分PDF文件。以下是一个示例代码, import fitz # PyMuPDF def split_pdf(i…...

IntelliJ IDEA 常用快捷键一览表(通用型,提高编写速度,类结构、查找和查看源码,替换与关闭,调整格式)
文章目录 IntelliJ IDEA 常用快捷键一览表1-IDEA的日常快捷键第1组:通用型第2组:提高编写速度(上)第3组:提高编写速度(下)第4组:类结构、查找和查看源码第5组:查找、替换…...
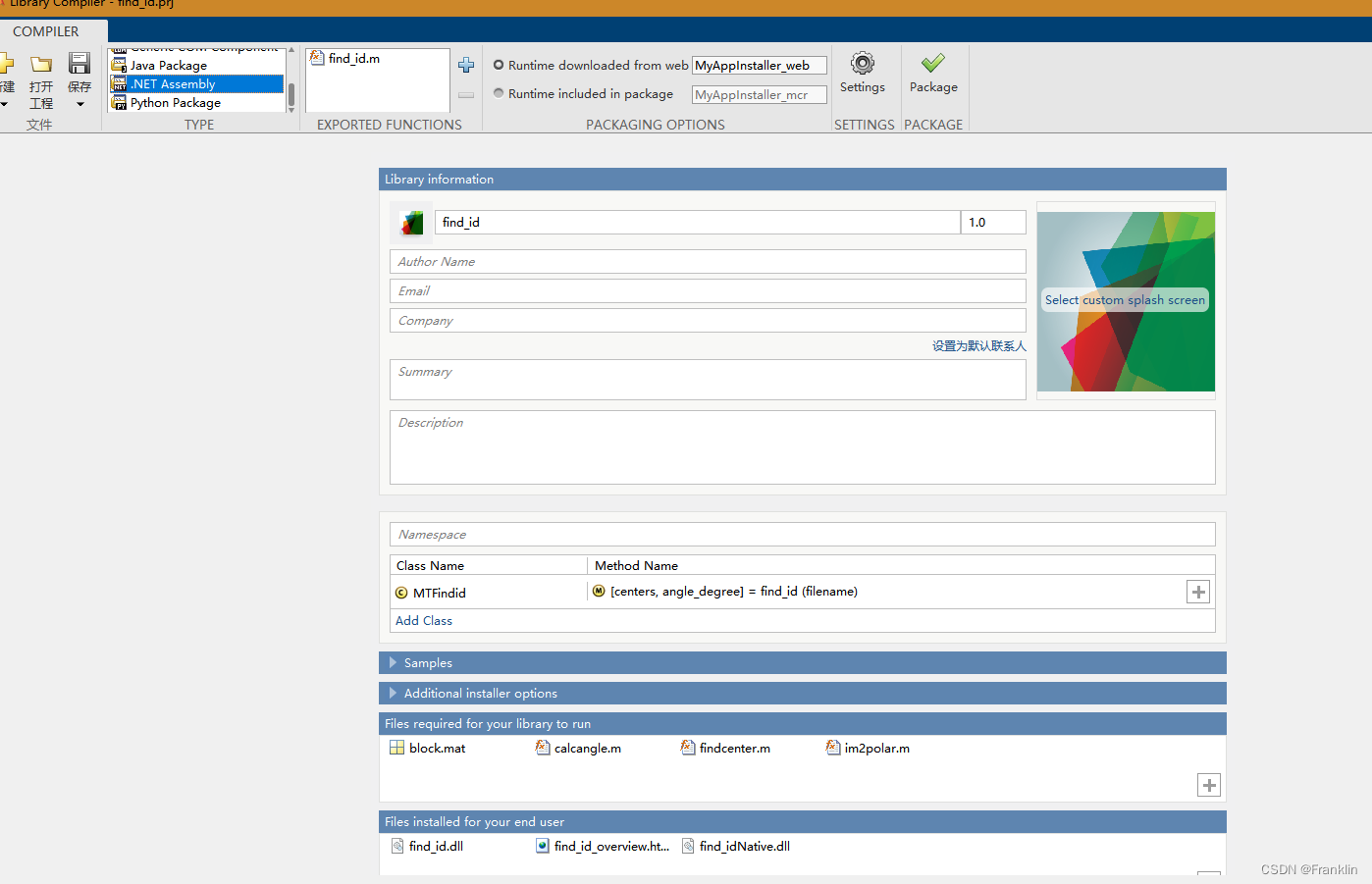
MSVS C# Matlab的混合编程系列2 - 构建一个复杂(含多个M文件)的动态库:
前言: 本节我们尝试将一个有很多函数和文件的Matlab算法文件集成到C#的项目里面。 本文缩语: MT = Matlab 问题提出: 1 我们有一个比较复杂的Matlab文件: 这个MATLAB的算法,写了很多的算法函数在其他的M文件里面,这样,前面博客的方法就不够用了。会报错: 解决办法如下…...

上位机图像处理和嵌入式模块部署(qt图像处理)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 很多人一想到图像处理,本能的第一反应就是opencv,这也没有错。但是呢,这里面还是有一个问题的,不知…...

AI教我学编程之C#类的实例化与访问修饰符
前言 在这篇文章中,我将带大家深入了解C#编程语言的核心概念,包括类的实例化、访问修饰符的应用,以及C#中不同数据类型的默认值。我会通过逐步分析和具体实例,详细解释如何在C#中正确创建和操作对象,并探讨如何通过访…...
【笔记】Blender4.0建模入门-3物体的基本操作
Blender入门 ——邵发 3.1 物体的移动 演示: 1、选中一个物体 2、选中移动工具 3、移动 - 沿坐标轴移动 - 在坐标平面内移动 - 自由移动(不好控制) 选中物体:右上的大纲窗口,点击物体名称,物体的轮…...

一文详解 Berachain 测试网:全面介绍与教程,bitget wallet教程
什么是Berachain? Berachain(web3.bitget.com/zh-CN/assets/berachain-wallet)是一种尖端区块链技术,使用 Cosmos SDK 构建的 Layer-1,兼容以太坊虚拟机(EVM)。它基于一种独特的概念,…...
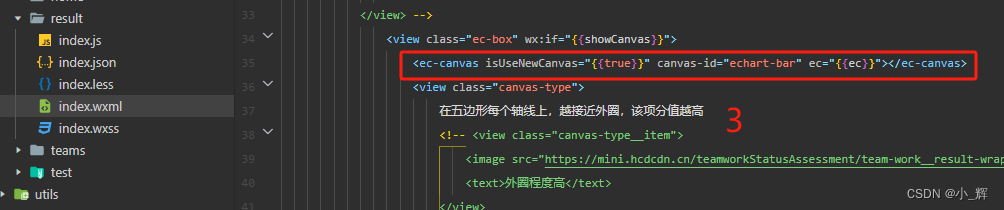
小程序使用echarts图表-雷达图
本文介绍下小程序中如何使用echarts 如果是通过npm安装,这样是全部安装的,体积有点大 我这边是使用echarts中的一个组件来实现的,下边是具体流程,实际效果是没有外边的红色边框的,加红色边框的效果是这篇说明 1.echa…...
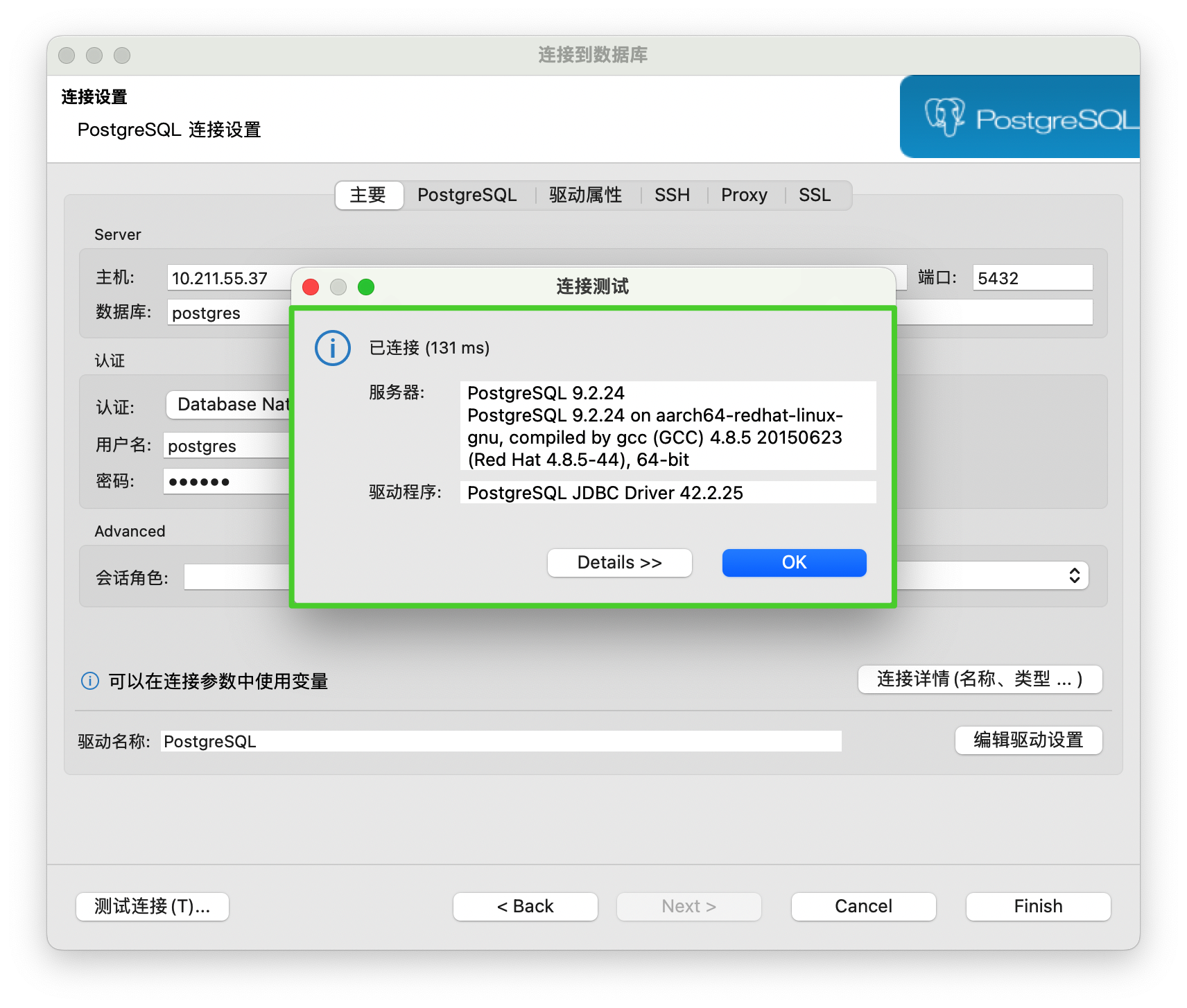
MacM1Pro Parallels19.1.0 CentOS7.9 Install PostgrepSQL
相关阅读 MacM1Pro安装 Parallels Desktop 19.1.0 https://blog.csdn.net/qq_41594280/article/details/135420241 MacM1Pro Parallels安装Parallels Tools https://blog.csdn.net/qq_41594280/article/details/135398780 MacM1Pro Parallels安装CentOS7.9 https://blog.csdn.n…...

Golang 中如何实现 Set
在Go编程中,数据结构的选择对解决问题至关重要。本文将探讨如何在 GO 中实现 set 和 bitset 两种数据结构,以及它们在Go中的应用场景。 Go 的数据结构 Go 内置的数据结构并不多。工作中,我们最常用的两种数据结构分别是 slice 和 map&#…...
记录一下uniapp 集成腾讯im特别卡(已解决)
uniapp的项目运行在微信小程序 , 安卓 , ios手机三端 , 之前这个项目集成过im,不过版本太老了,0.x的版本, 现在需要添加客服功能,所以就升级了 由于是二开 , 也为了方便 , 沿用之前的webview嵌套腾讯IM的方案 , 选用uniapp集成ui ,升级之后所有安卓用户反馈点击进去特别卡,几…...

React16源码: React中的updateHostRoot的源码实现
HostRoot 的更新 1 )概述 HostRoot 是一个比较特殊的节点, 因为在一个react应用当中它只会有一个 HostRoot, 它对应的 Fiber 对象是我们的 RootFiber 对象重点在于它的更新过程 2 )源码 定位到 packages/react-reconciler/src/ReactFiberBeginWork.js…...

Template -- React
React 版本 Node 21.6.0Npm 10.2.4 项目 创建 npm init vite 项目名称reactjsnpm inpm run dev 依赖 npm i axios # 网络 npm i antd --save # UI npm i ant-design/icons npm i react-router-dom # 路由npm i sass -D # …...

HTML 入门手册(一)
目录 HTML 1-基础语法 单标签 双标签 整体结构 2-标题和水平线 标题 水平线 3-段落和换行 段落 换行 4-列表 无序列表 有序列表 嵌套列表 5-div和span div span 6-格式化标签 粗体 斜体 下划线中划线 上标和下标 7-超链接(a标签) 链接到URL 链接到本…...

GPT帮我快速解决工作上的问题案例
Python入门容易,但精通不易。自从跟着郭老师学Python后,工作中也想偷点懒,之前排班表的问题一直困扰着我,福音来了,现在随着郭老师的小蜜蜂AI出来,说干就干。马上来到郭老师为我们提供的AI网站:…...

Day32- 贪心算法part06
一、单调递增的数字 题目一:738. 单调递增的数字 738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递…...

.NetCore Flurl.Http 升级到4.0后 https 无法建立SSL连接
Flurl.Http-3.2.4 升级到 4.0.0 版本后,https请求异常:Call failed. The SSL connection could not be established. 如下图: Flurl.Http-3.2.4版本绕过https的代码,对于 Flurl.Http-4.0.0 版本来说方法不再适用,3.2.…...

【每周AI简讯】GPT-5将有指数级提升,GPT Store正式上线
AI7 - Chat中文版最强人工智能 OpenAI的CEO奥特曼表示GPT-5将有指数级提升 GPT奥特曼参加Y-Combinator W24启动会上表示,我们已经非常接近AGI。GPT-5将具有更好的推理能力、更高的准确性和视频支持。 GPT Store正式上线 OpenAI正式推出GPT store,目前…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
