红黑树浅浅学习
红黑树浅浅学习
- 红黑树概念
- 红黑树平衡性调整
红黑树概念
- 二叉树:二叉树是每个节点最多有两个子树的树结构。
- 二叉查找树:又称“二叉搜索树”,左孩子比父节点小,右孩子比父节点大,还有一个特性就是”中序遍历“可以让结点有序。
- 平衡二叉树:它是一颗空树或者它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一颗平衡二叉树。
- 红黑树是一种自平衡的二叉查找树,它属于平衡树,但是却没有平衡二叉树那么“平衡”。可以保证在最坏情况下基本动态操作的时间复杂度为O(log n)。
- 红黑树中的每个节点都有一个颜色属性,可以是红色或黑色。
红黑树满足以下5个性质:
- 每个节点要么是红色的,要么是黑色的,根节点是黑色的。
- 每个叶子节点(NIL节点,空节点)是黑色的。
- 任何相邻节点不能同时为红色。
- 任何叶子节点,到根节点,所经过的黑节点数目相同。
- 当前节点到其所有叶节点包含的黑色节点数量相同。
通过这些性质,红黑树可以保证在插入和删除节点时,自动调整树的结构,以保持树的平衡和性质的满足。相比于普通的二叉查找树,红黑树的平衡性更好,查找、插入和删除都具有更稳定的时间复杂度,因此在很多场景下被广泛应用。

红黑树平衡性调整
- 依次插入 100 90 120,不需要进行平衡性调整
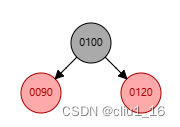
- 插入85,把90和120变成黑色,100变成红色。但100必须为黑色,100也变成黑色
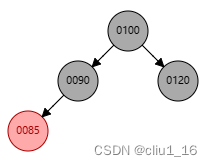
平衡性调整情况1:爷节点为黑色,父节点为红色,且有叔节点为红色,父亲节点为爷节点的左孩子
- 将父节点和叔节点都变为黑色。
- 爷节点变成红色
- 若爷节点变色之后红黑树性质出现问题,需要沿着爷节点继续向上调整
- 若爷节点为根节点,要变黑色。
- 插入60为红色,红黑树继续进行调整,85变成黑色,90变成红色。
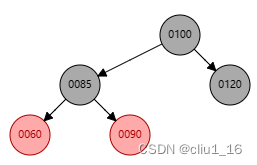
平衡性调整情况2:爷节点为黑色,父节点为红色,没有叔节点或叔节点为黑色,父亲节点为爷节点的左孩子,插入的节点是父节点的左孩子
平衡性调整情况3:爷节点为黑色,父节点为红色,没有叔节点或叔节点为黑色,父亲节点为爷节点的右孩子,插入的节点是父节点的左孩子
平衡性调整情况4-6分别为1-3的反情况
#include <iostream>
#include <list>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <assert.h>
#include <sstream>
#include <stack>using namespace std;template<typename T>
struct RBNode{T data;RBNode* leftChild;RBNode* rightChild;RBNode* parentNd;bool isRed; //判断是否为红色节点。
};template<typename T>
class RBTree{
public:RBTree():root(nullptr){}~RBTree(){ReleaseNode(root);}void InsertElem(const T&e){InsertElem(root,e);}void InsertElem(RBNode<T>*& tNode, const T& e){ //第一个参数类型:指针引用RBNode<T>* point = tNode; // 从指向根节点开始RBNode<T>* parent = nullptr; // 保存父节点,根节点的父节点先为nullptr// 通过一个while循环寻找要插入节点的位置,同时还要把插入路线上所经过的所有节点都保存到栈中,因为这些节点的平衡因子可能要调整。while(point !=nullptr){if(e==point->data) return; //要插入的数据和当前树中某节点的数据相同,不允许插入parent = point; // 记录父节点if(e > point->data){point = point->rightChild;}else{point = point->leftChild;}}// end while// 走到这里,point 等于nullptr,该生成新节点了point = new RBNode<T>;point->data = e;point->leftChild = nullptr;point->rightChild = nullptr;point->parentNd = nullptr;point->isRed = true; //缺省插入的节点先给红色,之后才会判断需不需要进行调整if(parent == nullptr){// 创建的是根节点point->isRed = false;tNode = point;return;} // 创建的不是根节点,要把节点链接到父节点上if(e > parent->data){parent->rightChild = point;}else{parent->leftChild = point;}point->parentNd = parent;if(parent->isRed == false) return; //如果父节点是黑色,当前插入的又是红色节点,不需要做什么直接返回BalanceTune(point,parent);// 不管前面经历了什么,根节点固定黑色root->isRed = false;}private:// 获取兄弟节点指针RBNode<T>* getBrotherNode(RBNode<T>* p){// 由调用者确认p->parent 一定不为nullptrif(p->parentNd->leftChild == p){return p->parentNd->rightChild;}return p->parentNd->leftChild; }// 平衡性调整void BalanceTune(RBNode<T>* point, RBNode<T>* parent){// 能走到这里的,要插入的节点肯定至少在第三层了,因为如果是第二层,那么插入的节点都是红色的,父节点肯定是黑色的// 父节点为红色才能走下来(当前节点为红色,此时需要进行平衡性调整)RBNode<T>* parentBroNode = nullptr; //叔节点,可能不存在RBNode<T>* grandFatherNode = nullptr; //爷节点,因为父节点为红色,红色不能为根,那么至少都是爷节点做根while(true){parentBroNode = (parent->parentNd !=nullptr) ? (getBrotherNode(parent)):nullptr; //叔节点grandFatherNode = point->parentNd->parentNd; //爷节点// 不断向上调整,爷节点可能有为空的时候if(grandFatherNode == nullptr) break;// 如果叔节点为红色,那么爷节点不可能为红色if(parentBroNode != nullptr && parentBroNode->isRed == true){//平衡性调整情况1,没有将爷节点置为黑色的原因是统一在外部进行根节点为黑色的设置// 先处理变色问题// (1)父节点和叔节点变为黑色,爷节点变为红色parent->isRed = false;parentBroNode->isRed = false;grandFatherNode->isRed = true;// (2)如果爷节点是根,跳出循环,根节点颜色在循环外进行设置为黑色的处理if(grandFatherNode == root) break;// (3) 往上走继续循环point = grandFatherNode;parent = point->parentNd;if(parent->isRed = false) break;continue;} // 能走到这里的平衡性调整情况2,不满足if(parentBroNode != nullptr && parentBroNode->isRed == true)// 叔节点为黑色或叔节点为空的情况// 旋转变色之前的一些信息,这是通用代码RBNode<T>* gff = grandFatherNode->parentNd; //太爷节点int sign = 0; // 标记1:grandFatherNode是父节点的左孩子,标记2:grandFatherNode是父节点的右孩子。if(gff!=nullptr){if(gff->leftChild == grandFatherNode){sign = 1;}else{sign = 2;}}if(grandFatherNode->leftChild == parent){ //第一种情形,父亲是爷节点的左孩子// 开始旋转和变色以调整平衡if(parent->leftChild == point){ //新节点是父亲节点的左孩子// 右旋转RotateRight(grandFatherNode);}else{ //新节点是父亲节点的右孩子// 先左旋后右旋RotateLeftRight(grandFatherNode);}// 旋转之后变色的代码,通用grandFatherNode->isRed = false; //新的根节点设置为黑色grandFatherNode->rightChild->isRed = true; //新右叶子设置为红色}else{ // 第二种情形,父亲是爷节点的右孩子if(parent->rightChild == point){ //新节点是父亲的右孩子RotateLeft(grandFatherNode);}else{RotateRightLeft(grandFatherNode);}// 旋转变色之后的一些公用代码grandFatherNode->isRed = false; //新根设置为黑色grandFatherNode->leftChild->isRed = true; //新左叶子设置为红色}//*** 一些通用代码// 根已经改变了,所以要设置一些节点指向信息if(gff == nullptr){root = grandFatherNode;}else if(sign == 1){gff->leftChild = grandFatherNode;}else if(sign == 2){gff->rightChild = grandFatherNode;}break;}// end while(true)return;}// 右旋转void RotateRight(RBNode<T>*& pointer){ //注意参数类型RBNode<T>* ptmproot = pointer;pointer = ptmproot->leftChild;pointer->parentNd = ptmproot->parentNd;ptmproot->leftChild = pointer->rightChild;if(pointer->rightChild){pointer->rightChild->parentNd =ptmproot;}pointer->rightChild = ptmproot;ptmproot->parentNd = pointer;}void ReleaseNode(RBNode<T>* pnode){if(pnode !=nullptr){ReleaseNode(pnode->leftChild);ReleaseNode(pnode->rightChild);}delete pnode;}private:RBNode<T>* root;
};int main()
{RBTree<int> myrbtr;int array[] = {80,50,120,30,60,20,40};int acount = sizeof(array)/sizeof(int);for(int i=0;i<acount;i++){myrbtr.InsertElem(array[i]);}return 0;
}= =
相关文章:

红黑树浅浅学习
红黑树浅浅学习 红黑树概念红黑树平衡性调整 红黑树概念 二叉树:二叉树是每个节点最多有两个子树的树结构。二叉查找树:又称“二叉搜索树”,左孩子比父节点小,右孩子比父节点大,还有一个特性就是”中序遍历“可以让结…...

QGraphicsView 如何让图形大小适配窗口
1. setSceneRect 做什么用? setSceneRect是一个Qt中的函数,用于设置QGraphicsView中的场景矩形(QRectF)。 QGraphicsView是一个用于显示和编辑图形场景的控件,而setSceneRect函数用于设置场景矩形,即指定…...

sqlmap使用教程(3)-探测注入漏洞
1、探测GET参数 以下为探测DVWA靶场low级别的sql注入,以下提交方式为GET,问号(?)将分隔URL和传输的数据,而参数之间以&相连。--auth-credadmin:password --auth-typebasic (DVWA靶场需要登录…...

期待已久!阿里云容器服务 ACK AI 助手正式上线
作者:行疾 大模型技术的蓬勃发展持续引领 AI 出圈潮流,各行各业都在尝试采用 AI 工具实现智能增效。 2023 年云栖大会上,阿里云容器服务团队正式发布 ACK AI 助手,带来大模型增强智能诊断,帮助企业和开发者降低 K8s …...
[BUG] Authentication Error
前言 给服务器安装了一个todesk,但是远程一直就是,点击用户,进入输入密码界面,还没等输入就自动返回了 解决 服务器是无桌面版本,或者桌面程序死掉了,重新安装就好 sudo apt install xorg sudo apt inst…...

23种设计模式概述
学习设计模式对我们有什么帮助? 1.提高代码质量和可维护性:设计模式是经过验证的解决方案,有助于解决常见的设计问题。使用设计模式可以减少代码冗余,增强代码的可读性和可维护性,并提高代码的可靠性。 2.提升开发效率…...

英文阅读-LinkedIn‘s Tips for Highly Effective Code Review
LinkedIn的CR技巧 LinkedIn团队CodeReview经验与方法,原文来自https://thenewstack.io/linkedin-code-review/ 总结 Do I Understand the “Why”? 在提交pr的同时需要描述本次修改的“动机”,有助于提高代码文档质量。 Am I Giving Positive Feedbac…...
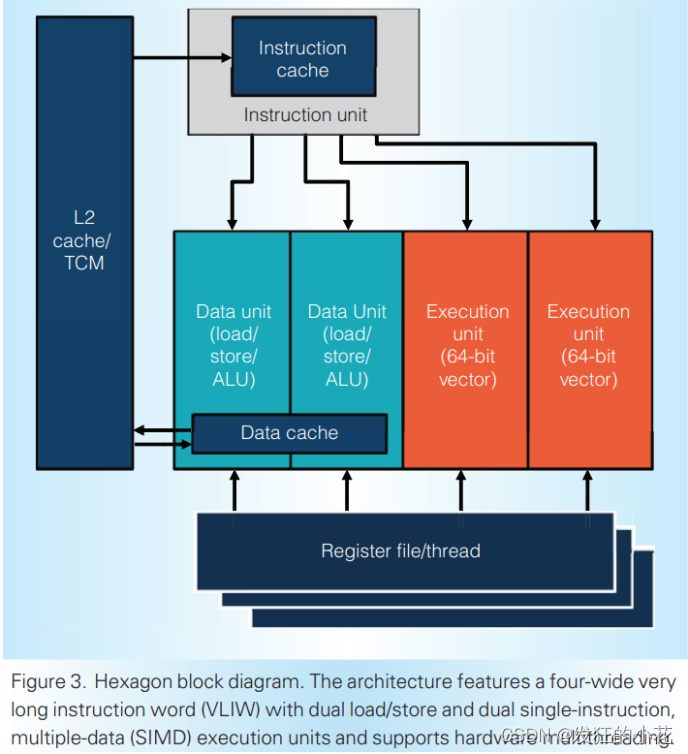
性能优化-高通的Hexagon DSP和NPU
原文来自【 Qualcomm’s Hexagon DSP, and now, NPU 】 本文主要介绍Qualcomm Hexagon DSP和NPU,这些为处理简单大量运算而设计的硬件。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能…...

第137期 Oracle的数据生命周期管理(20240123)
数据库管理137期 2024-01-23 第137期 Oracle的数据生命周期管理(20240123)1 ILM2 Heat Map3 ADO4 优点5 对比总结 第137期 Oracle的数据生命周期管理(20240123) 作者:胖头鱼的鱼缸(尹海文) Orac…...
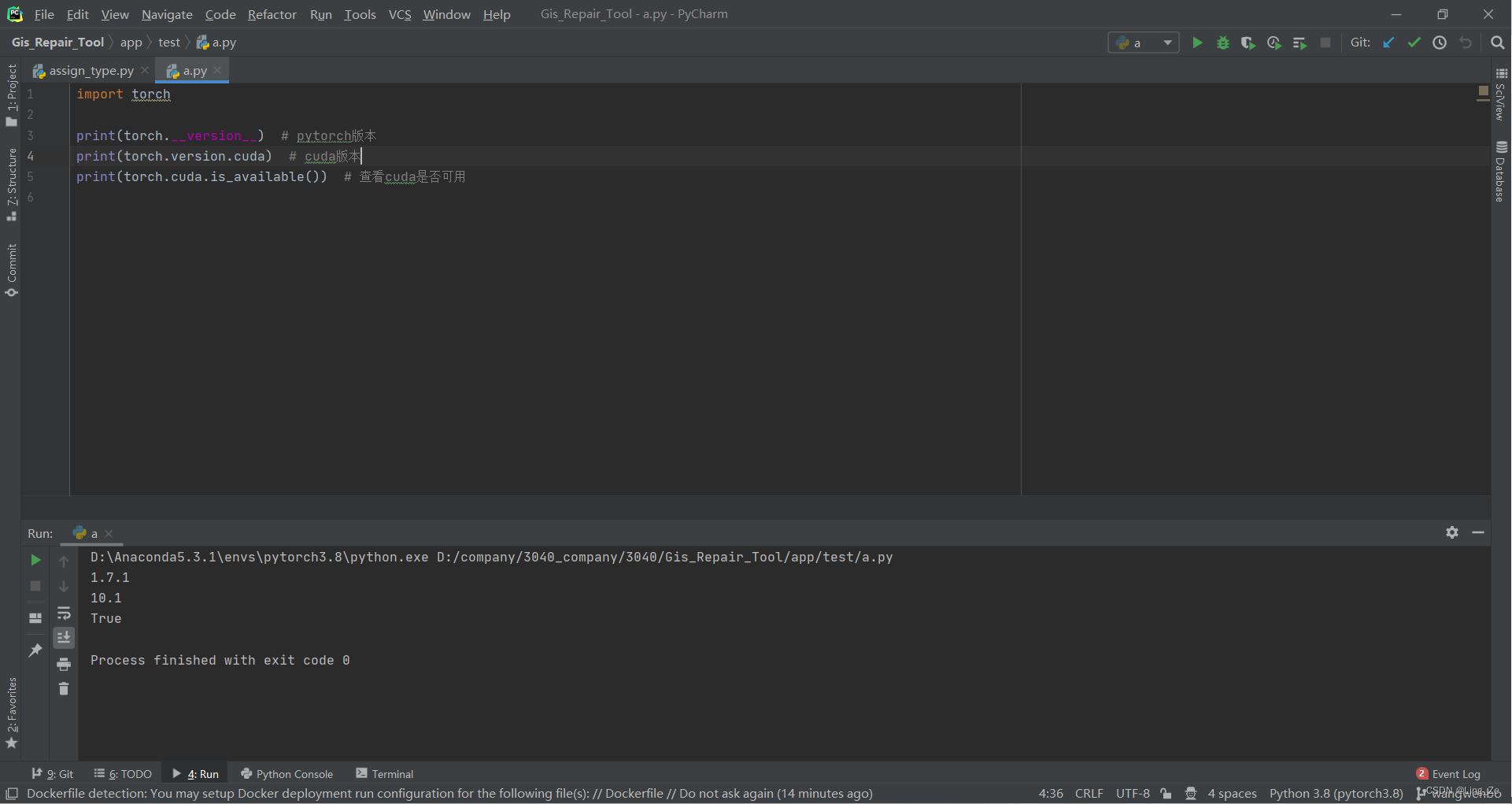
电脑的GPU太强了,pytorch版本跟不上,将cuda驱动进行降级
我的情况: 我买的电脑的GPU版本为rtx4060,但是装上相应的驱动后,cuda的版本为12.3,而现在pytorch中cuda安装命令的最新版本为12.1,所以我将电脑的驱动进行降级为cuda版本为10.1的。 最后成功安装cuda10.1版本的驱动 …...
1 认识微服务
1.认识微服务 随着互联网行业的发展,对服务的要求也越来越高,服务架构也从单体架构逐渐演变为现在流行的微服务架构。这些架构之间有怎样的差别呢? 1.0.学习目标 了解微服务架构的优缺点 1.1.单体架构 单体架构:将业务的所有…...

PHP+SOCKET 服务端多进程处理多客户端请求 demo
服务端 $socket socket_create(AF_INET,SOCK_STREAM,SOL_TCP); socket_bind($socket,0,95012) or die( server bind fail: . socket_strerror(socket_last_error())); socket_listen($socket,5);$child 0; //初始化子进程数 while(true){$client socket_accept($socket);$pi…...
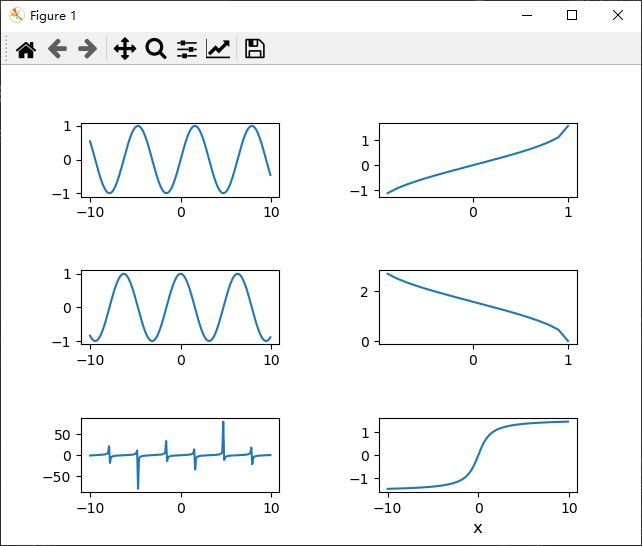
Matplotlib笔记:安装Matplotlib+常用绘图
Matplotlib Python的2D绘图库 安装Matplotlib 打开Anaconda Prompt切换环境(默认是base,无需切换)输入命令行安装pip install -i https://pypi.tuna.tsinghua.edu.cn/simple matplotlib3.5.2 绘图 导入import matplotlib.pyplot as plt …...
Confluence6+mysql5.7安装避坑详细记录
目录 一、前言 二、下载与安装 1、版本和安装环境 2、安装数据库 3、配置数据库 4、安装confluence 三、Pj confluence 1、选择语言和产品安装 2、Pj 3、上传mysql驱动 4、重启Confluence服务继续安装 四、Confluence重启卸载方法 重启方法 方法一 方法二 卸载…...

YTM32的HSM模块在信息安全场景中的应用
YTM32的HSM模块在信息安全场景中的应用 文章目录 YTM32的HSM模块在信息安全场景中的应用引言应用场景:一点点密码学基础硬件:YTM32的信息安全子系统HCU外设模块硬件特性基本的应用操作流程,以计算AES-ECB为例硬件上对处理多块数据上的一些设计…...
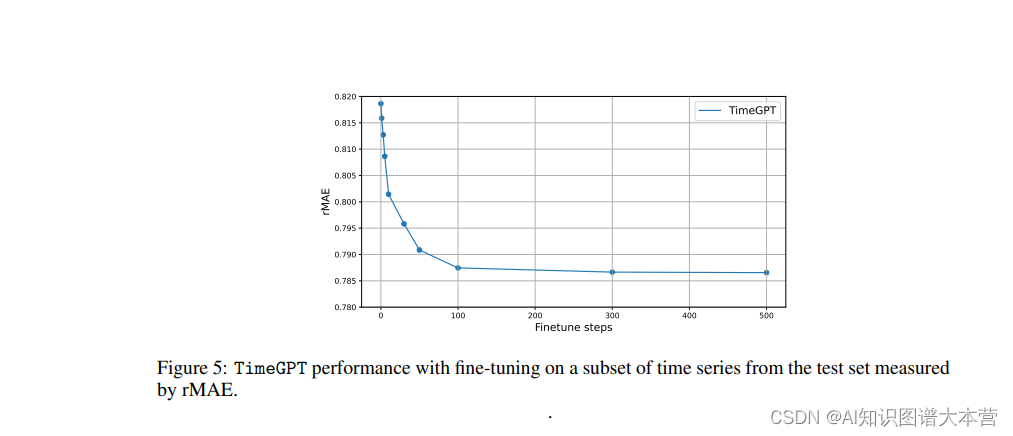
时间序列大模型:TimeGPT
论文:https://arxiv.org/pdf/2310.03589.pdf TimeGPT,这是第一个用于时间序列的基础模型,能够为训练期间未见过的多样化数据集生成准确的预测。 大规模时间序列模型通过利用当代深度学习进步的能力,使精确预测和减少不确定性成为…...
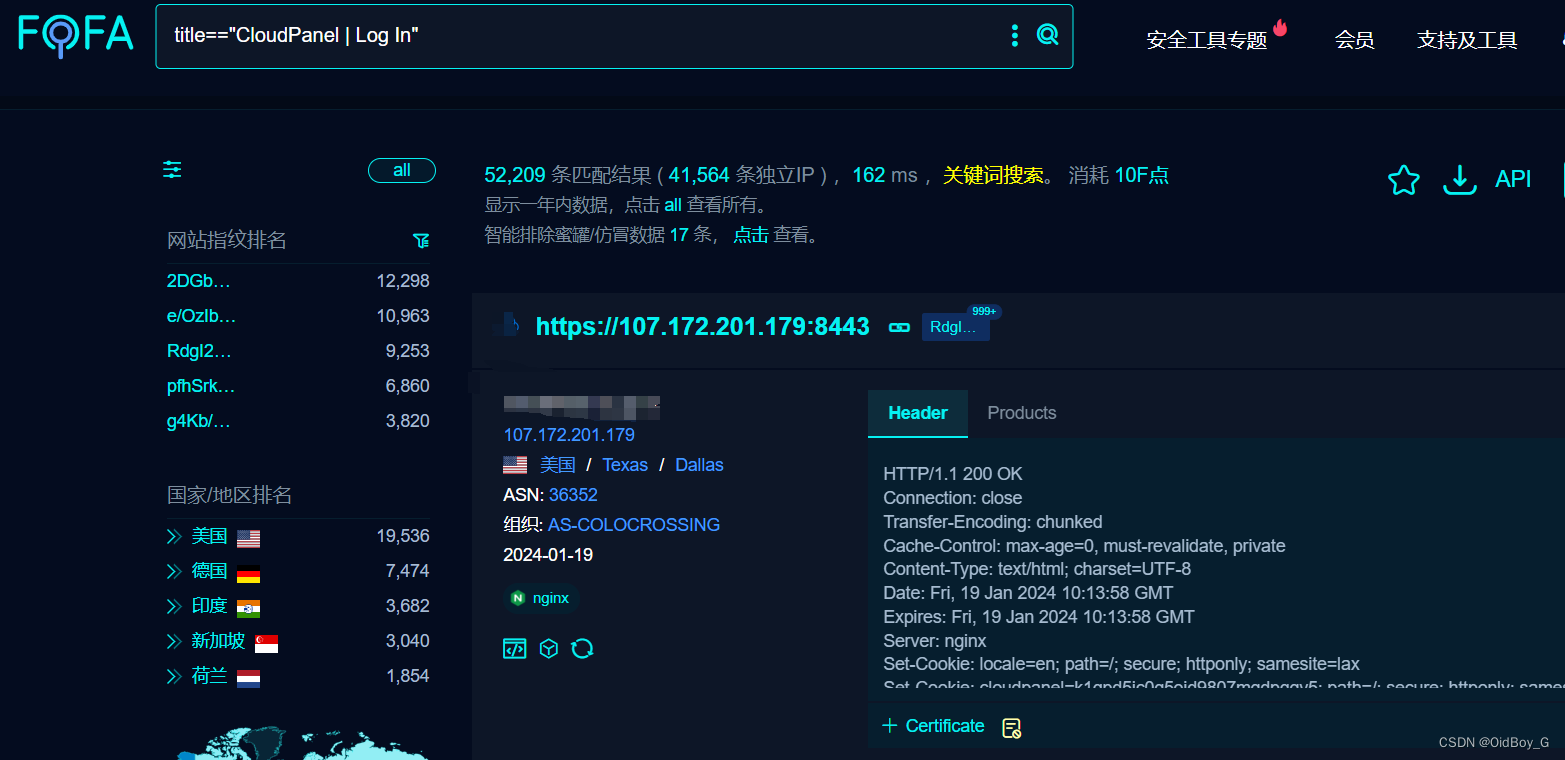
CloudPanel RCE漏洞复现(CVE-2023-35885)
0x01 产品简介 CloudPanel 是一个基于 Web 的控制面板或管理界面,旨在简化云托管环境的管理。它提供了一个集中式平台,用于管理云基础架构的各个方面,包括虚拟机 (VM)、存储、网络和应用程序。 0x02 漏洞概述 由于2.3.1 之前的 CloudPanel 具有不安全的文件管理器 cook…...
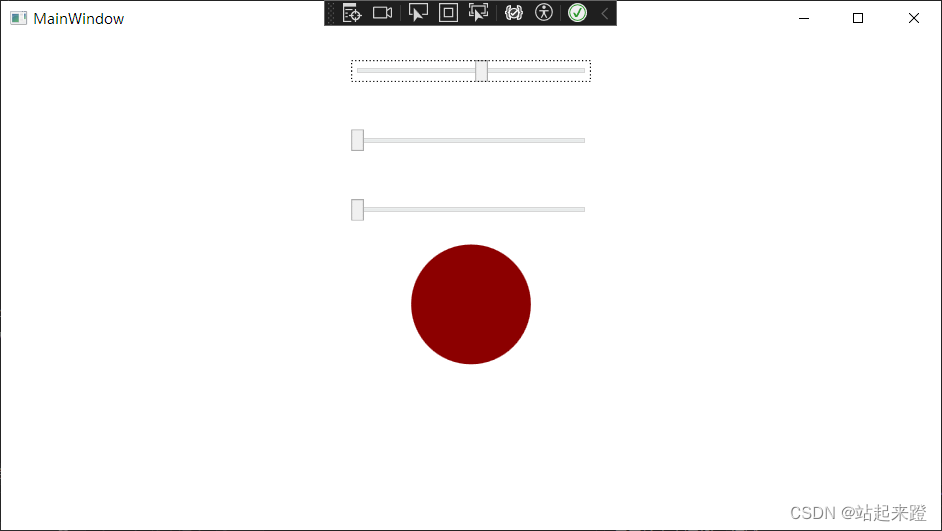
WPF多值转换器
背景:实现Slider拖动可以调整rgb 单转换器:WPF中数据绑定转换器Converter-CSDN博客 在View中: <StackPanel Orientation"Vertical"><Slider x:Name"slider_R" Minimum"0" Maximum"255" Wi…...

x-cmd pkg | perl - 具有强大的文本处理能力的通用脚本语言
目录 介绍首次用户技术特点竞品进一步阅读 介绍 Perl 是一种动态弱类型编程语言。Perl 内部集成了正则表达式的功能,以及巨大的第三方代码库 CPAN;在处理文本领域,是最有竞争力的一门编程语言之一 生态系统:综合 Perl 档案网络 (CPAN) 提供了超过 25,0…...
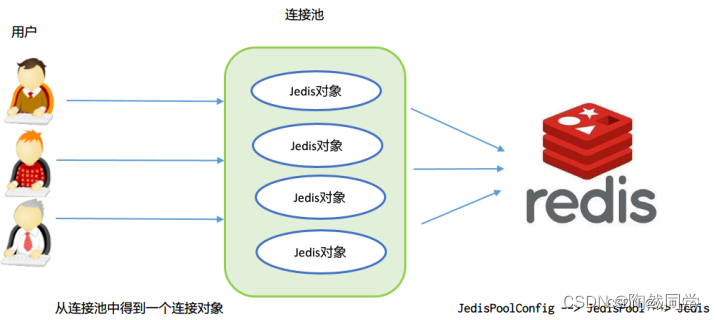
Jedis(一)与Redis的关系
一、Jedis介绍: 1、背景: Jedis是基于Java语言的Redis的客户端,Jedis Java Redis。Redis不仅可以使用命令来操作,现在基本上主流的语言都有API支持,比如Java、C#、C、PHP、Node.js、Go等。在官方网站里有一些Java的…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
