【算法专题】动态规划之路径问题
动态规划2.0
- 动态规划 - - - 路径问题
- 1. 不同路径
- 2. 不同路径Ⅱ
- 3. 珠宝的最高价值
- 4. 下降路径最小和
- 5. 最小路径和
- 6. 地下城游戏
动态规划 - - - 路径问题
1. 不同路径
题目链接 -> Leetcode -62.不同路径
Leetcode -62.不同路径
题目:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右->向下->向下
- 向下->向下->向右
- 向下->向右->向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
- 1 <= m, n <= 100
- 题目数据保证答案小于等于 2 * 10^9
思路:
- 状态表示:对于这种「路径类」的问题,我们的状态表示一般有两种形式:
i. 从 [i, j] 位置出发,…;
ii. 从起始位置出发,到达 [i, j] 位置,…;
我们选择第二种定义状态表示的方式:dp[i][j] 表示:走到 [i, j] 位置处,一共有多少种方式。 - 状态转移方程:分析一下,如果 dp[i][j] 表示到达 [i, j] 位置的方法数,那么到达 [i, j] 位置之前的一小步,有两种情况:
i. 从 [i, j] 位置的上方( [i - 1, j] 的位置)向下走一步,转移到 [i, j] 位置;
ii. 从 [i, j] 位置的左方( [i, j - 1] 的位置)向右走一步,转移到 [i, j] 位置。
由于我们要求的是有多少种方法,因此状态转移方程就呼之欲出了: dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 。 - 返回值:根据状态表示,我们要返回 dp[m][n] 的值。
代码如下:
class Solution {public:int uniquePaths(int m, int n){// 多开一行一列,可以直接在循环内初始化vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1; // 为了后面填表的正确// dp[i][j] 表示:⾛到 [i, j] 位置处,⼀共有多少种方式for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}};
2. 不同路径Ⅱ
题目链接 -> Leetcode -63.不同路径Ⅱ
Leetcode -63.不同路径Ⅱ
题目:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
输入:obstacleGrid = [[0, 0, 0], [0, 1, 0], [0, 0, 0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右->向右->向下->向下
- 向下->向下->向右->向右
示例 2:
输入:obstacleGrid = [[0, 1], [0, 0]]
输出:1
提示:
- m == obstacleGrid.length
- n == obstacleGrid[i].length
- 1 <= m, n <= 100
- obstacleGrid[i][j] 为 0 或 1
思路:本题为不同路径的变型,只不过有些地方有「障碍物」,只要在「状态转移」上稍加修改就可解决。
- 状态表示:dp[i][j] 表示:走到 [i, j] 位置处,一共有多少种方式。
- 状态转移:简单分析一下。如果 dp[i][j] 表示到达 [i, j] 位置的方法数,那么到达 [i, j] 位置之前的一小步,有两种情况:
i. 从 [i, j] 位置的上方( [i - 1, j] 的位置)向下走一步,转移到 [i, j] 位置;
ii. 从 [i, j] 位置的左方( [i, j - 1] 的位置)向右走一步,转移到 [i, j] 位置。
但是, [i - 1, j] 与 [i, j - 1] 位置都是可能有障碍的,此时从上面或者左边是不可能到达 [i, j] 位置的,也就是说,此时的方法数应该是 0;由此我们可以得出一个结论,只要这个位置上「有障碍物」,那么我们就不需要计算这个位置上的值,直接让它等于 0 即可。 - 返回值:根据状态表示,我们要返回的结果是 dp[m][n].
代码如下:
class Solution {public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid){int m = obstacleGrid.size(), n = obstacleGrid[0].size();// 多开一行一列方便初始化vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1; // 为了后面填表的正确// dp[i][j] 表示:⾛到 [i, j] 位置处,⼀共有多少种方式for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){// 原矩阵中的位置不是障碍物if (obstacleGrid[i - 1][j - 1] != 1){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}}return dp[m][n];}};
3. 珠宝的最高价值
题目链接 -> Leetcode -LCR 166.珠宝的最高价值
Leetcode -LCR 166.珠宝的最高价值
题目:现有一个记作二维矩阵 frame 的珠宝架,其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为:
只能从架子的左上角开始拿珠宝
每次可以移动到右侧或下侧的相邻位置
到达珠宝架子的右下角时,停止拿取
注意:珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝,比如 frame = [[0]] 。
示例 1:
输入: frame = [[1, 3, 1], [1, 5, 1], [4, 2, 1]]
输出 : 12
解释 : 路径 1→3→5→2→1 可以拿到最高价值的珠宝
提示:
- 0 < frame.length <= 200
- 0 < frame[0].length <= 200
思路:本题的思路与上题的思路差不多,状态转移方程为:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] .
代码如下:
class Solution {public:int maxValue(vector<vector<int>>& grid){int m = grid.size(), n = grid[0].size();// 多开一行一列方便初始化vector<vector<int>> dp(m + 1, vector<int>(n + 1));// dp[i][j] 表示:⾛到 [i, j] 位置处,此时的最大价值for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[m][n];}};
4. 下降路径最小和
题目链接 -> Leetcode -931.下降路径最小和
Leetcode -931.下降路径最小和
题目:给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。
在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。
具体来说,位置(row, col) 的下一个元素应当是(row + 1, col - 1)、(row + 1, col) 或者(row + 1, col + 1) 。
示例 1:
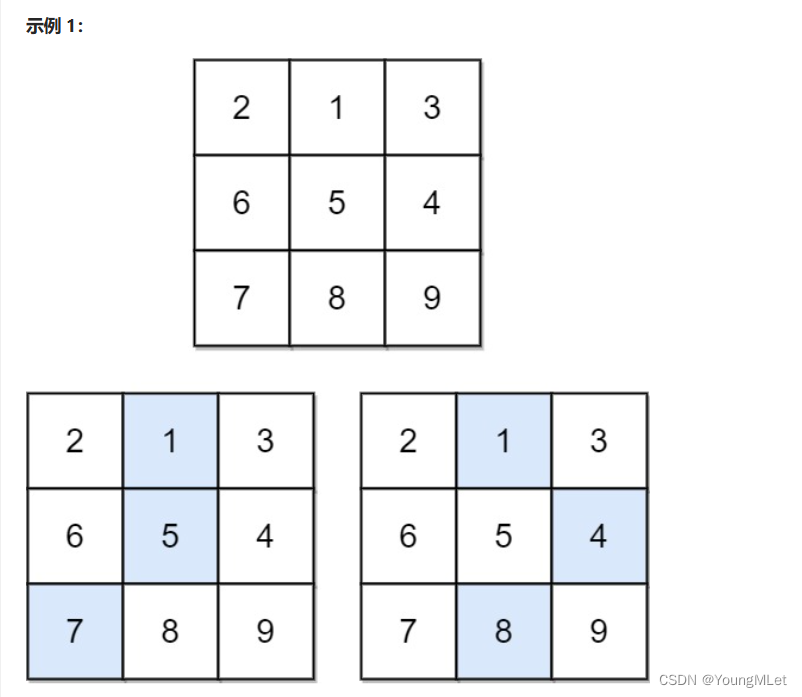
输入:matrix = [[2, 1, 3], [6, 5, 4], [7, 8, 9]]
输出:13
解释:如图所示,为和最小的两条下降路径
示例 2:
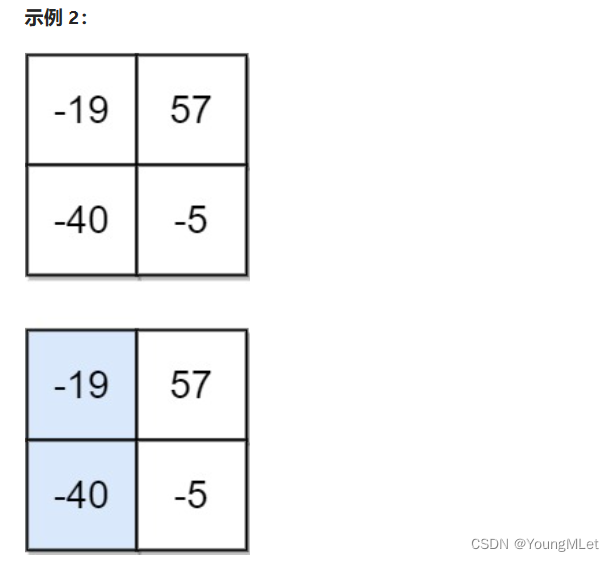
输入:matrix = [[-19, 57], [-40, -5]]
输出: - 59
解释:如图所示,为和最小的下降路径
提示:
- n == matrix.length == matrix[i].length
- 1 <= n <= 100
- 100 <= matrix[i][j] <= 100
思路:
- 状态表示:dp[i][j] 表示:到达 [i, j] 位置时,所有下降路径中的最小和。
- 状态转移方程:对于普遍位置 [i, j] ,根据题意得,到达 [i, j] 位置可能有三种情况:
i. 从正上方 [i - 1, j] 位置转移到 [i, j] 位置;
ii. 从左上方 [i - 1, j - 1] 位置转移到 [i, j] 位置;
iii. 从右上方 [i - 1, j + 1] 位置转移到 [i, j] 位置;
我们要的是三种情况下的「最小值」,然后再加上矩阵在 [i, j] 位置的值。
于是 dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i][j] 。 - 返回值:注意这里不是返回 dp[m][n] 的值;题目要求「只要到达最后一行」就行了,因此这里应该返回「 dp 表中最后一行的最小值」。
代码如下:
class Solution {public:int minFallingPathSum(vector<vector<int>>& matrix){int len = matrix.size();// 多开一行,两列,因为dp[i][j]的值需要用到dp[i - 1][j], dp[i - 1][j - 1], dp[i - 1][j + 1]vector<vector<int>> dp(len + 1, vector<int>(len + 2, INT_MAX));// 初始化,为了后面填表的正确性for (int i = 0; i <= len; i++) dp[0][i] = 0;// dp[i][j] 表示:到达 [i, j] 位置时,所有下降路径中的最小和for (int i = 1; i <= len; i++){for (int j = 1; j <= len; j++){dp[i][j] = min(min(dp[i - 1][j], dp[i - 1][j - 1]), dp[i - 1][j + 1]) + matrix[i - 1][j - 1];}}// 返回最后一行的最小值int ret = INT_MAX;for (int j = 0; j <= len; j++) ret = min(ret, dp[len][j]);return ret;}};
5. 最小路径和
题目链接 -> Leetcode -64.最小路径和
Leetcode -64.最小路径和
题目:给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
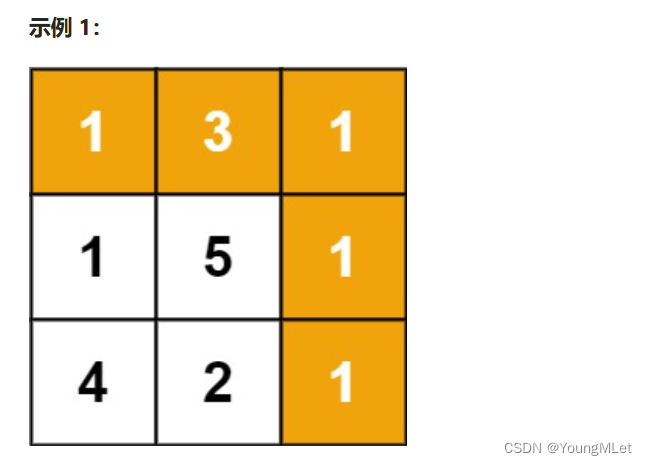
输入:grid = [[1, 3, 1], [1, 5, 1], [4, 2, 1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1, 2, 3], [4, 5, 6]]
输出:12
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
思路:
- 状态表示:dp[i][j] 表示:到达 [i, j] 位置处,最小路径和是多少
- 状态转移:分析一下,如果 dp[i][j] 表示到达 [i, j] 位置处的最小路径和,那么到达[i, j] 位置之前的一小步,有两种情况:
i. 从 [i - 1, j] 向下走一步,转移到 [i, j] 位置;
ii. 从 [i, j - 1] 向右走一步,转移到 [i, j] 位置。
由于到 [i, j] 位置两种情况,并且我们要找的是最小路径,因此只需要这两种情况下的最小值,再加上 [i, j] 位置上本身的值即可。也就是: dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] - 返回值:根据状态表示,我们要返回的结果是 dp[m][n].
代码如下:
class Solution {public:int minPathSum(vector<vector<int>>& grid){int m = grid.size(), n = grid[0].size();// dp[i][j] 表示:到达 [i, j] 位置处,最小路径和是多少vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[0][1] = 0;for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[m][n];}};
6. 地下城游戏
题目链接 -> Leetcode -174.地下城游戏
Leetcode -174.地下城游戏
题目:恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。
我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);
其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
输入:dungeon = [[-2, -3, 3], [-5, -10, 1], [10, 30, -5]]
输出:7
解释:如果骑士遵循最佳路径:右->右->下->下 ,则骑士的初始健康点数至少为 7 。
示例 2:
输入:dungeon = [[0]]
输出:1
提示:
- m == dungeon.length
- n == dungeon[i].length
- 1 <= m, n <= 200
- 1000 <= dungeon[i][j] <= 1000
思路:
- 状态表示:这道题如果我们定义成:从起点开始,到达 [i, j] 位置的时候,所需的最低初始健康点数。那么我们分析状态转移的时候会有一个问题:那就是我们当前的健康点数还会受到后面的路径的影响。也就是从上往下的状态转移不能很好地解决问题。
这个时候我们要换一种状态表示:从 [i, j] 位置出发,到达终点时所需要的最低初始健康点数。这样我们在分析状态转移的时候,后续的最佳状态就已经知晓。综上所述,定义状态表示为:dp[i][j] 表示:从 [i, j] 位置出发,到达终点时所需的最低初始健康点数。 - 状态转移方程:对于 dp[i][j] ,从 [i, j] 位置出发,下一步会有两种选择(为了方便理解,设 dp[i][j] 的最终答案是 x ):
i. 走到右边,然后走向终点;那么我们在 [i, j] 位置的最低健康点数加上这一个位置的消耗,应该要大于等于右边位置的最低健康点数,也就是: x + dungeon[i][j] >= dp[i][j + 1] ;通过移项可得: x >= dp[i][j + 1] - dungeon[i][j] 。因为我们要的是最小
值,因此这种情况下的 x = dp[i][j + 1] - dungeon[i][j] ;
ii. 走到下边,然后走向终点;那么我们在 [i, j] 位置的最低健康点数加上这⼀个位置的消耗,应该要大于等于下边位置的最低健康点数,也就是: x + dungeon[i][j] >= dp[i + 1][j] 。通过移项可得: x >= dp[i + 1][j] - dungeon[i][j] 。因为我们要的是最小值,因此这种情况下的 x = dp[i + 1][j] - dungeon[i][j] ;
- 综上所述,我们需要的是两种情况下的最小值,因此可得状态转移方程为:dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]
但是,如果当前位置的 dungeon[i][j] 是一个比较大的正数的话, dp[i][j] 的值可能变成 0 或者负数。也就是最低点数会小于 1 ,那么骑士就会死亡。因此我们求出来的 dp[i][j] 如果小于等于 0 的话,说明此时的最低初始值应该为 1 。处理这种情况仅需让 dp[i][j] 与 1 取一个最大值即可:dp[i][j] = max(1, dp[i][j])
-
初始化:可以在最前面加上一个「辅助结点」,帮助我们初始化。使用这种技巧要注意两个点:
i. 辅助结点里面的值要「保证后续填表是正确的」;
ii. 「下标的映射关系」。
在本题中,在 dp 表最后面添加一行,并且添加一列后,所有的值都先初始化为无穷大,然后让 dp[m][n - 1] = dp[m - 1][n] = 1 即可。 -
返回值:根据「状态表示」,我们需要返回 dp[0][0] 的值。
代码如下:
class Solution {public:int calculateMinimumHP(vector<vector<int>>& dungeon){int m = dungeon.size(), n = dungeon[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[m][n - 1] = 1;// 从右下角往回推for (int i = m - 1; i >= 0; i--){for (int j = n - 1; j >= 0; j--){dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];// 如果减到负数,说明这里的血包很大,即使是负数到这里都可以,但是这是不符合常理的// 所以需要将这里置成 1 即可if (dp[i][j] <= 0) dp[i][j] = 1; }}// 返回最初位置return dp[0][0];}};
相关文章:

【算法专题】动态规划之路径问题
动态规划2.0 动态规划 - - - 路径问题1. 不同路径2. 不同路径Ⅱ3. 珠宝的最高价值4. 下降路径最小和5. 最小路径和6. 地下城游戏 动态规划 - - - 路径问题 1. 不同路径 题目链接 -> Leetcode -62.不同路径 Leetcode -62.不同路径 题目:一个机器人位于一个 m …...

Python range函数
Python中的range()函数是一个强大的工具,用于生成一系列的整数。它在循环、迭代和序列生成等方面都有广泛的应用。本文将深入探讨range()函数的用法,提供详细的示例代码,并讨论其在Python编程中的实际应用。 什么是range()函数? …...
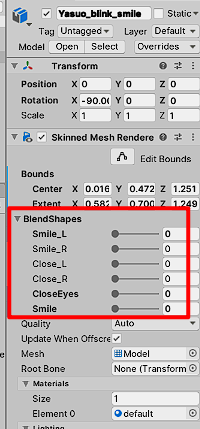
Unity中实现捏脸系统
前言 目前市面上常见的捏脸一般是基于BlendShapes和控制骨骼点坐标两种方案实现的。后者能够控制的精细程度更高,同时使用BlendShapes来控制表情。 控制骨骼点坐标 比如找到控制鼻子的骨骼节点修改localScale缩放,调节鼻子大小。 BlendShapes控制表…...
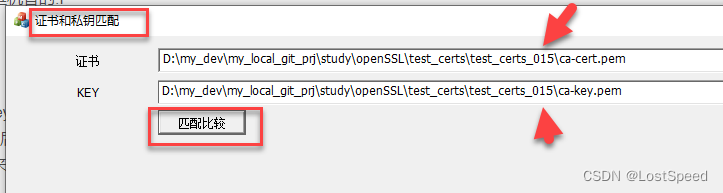
openssl3.2 - 检查rsa证书和私钥是否匹配(快速手搓一个工具)
文章目录 openssl3.2 - 检查rsa证书和私钥是否匹配(快速手搓一个工具)概述效果笔记编程环境界面控件的设置增加文件拖拽的类RSA证书和key是否匹配的实现在程序中加入环境变量备注备注END openssl3.2 - 检查rsa证书和私钥是否匹配(快速手搓一个工具) 概述 在学习openssl官方的…...
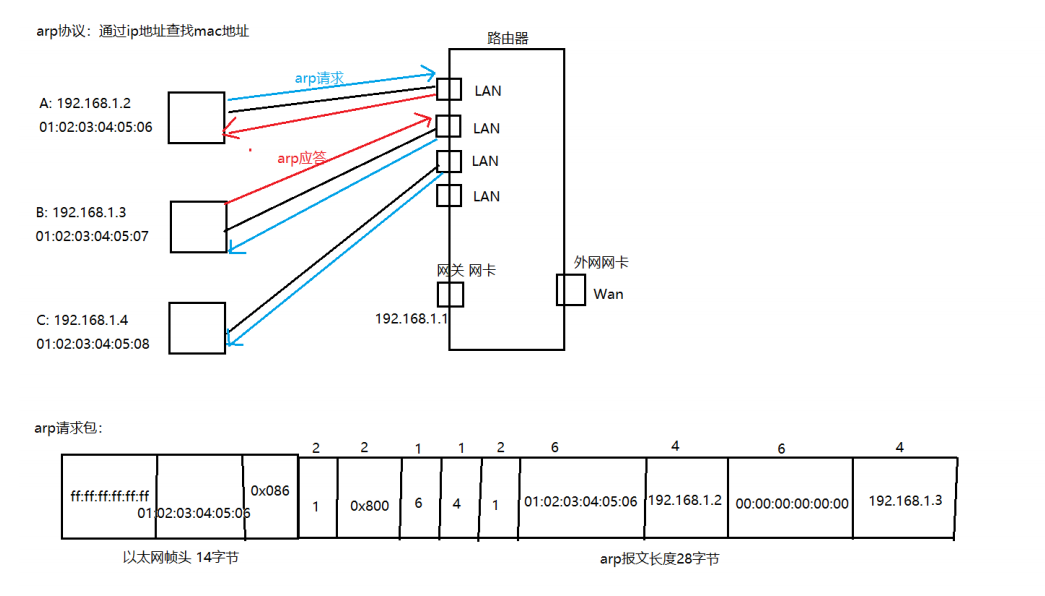
关于网络协议的笔记
简介: 协议, 网络协议的简称,网络协议是通信计算机双方必须共同遵从的一组约定。如怎么样建立连 接、怎么样互相识别等。只有遵守这个约定,计算机之间才能相互通信交流。它的 三要素是:语 法、语义、时序。 为了使数…...
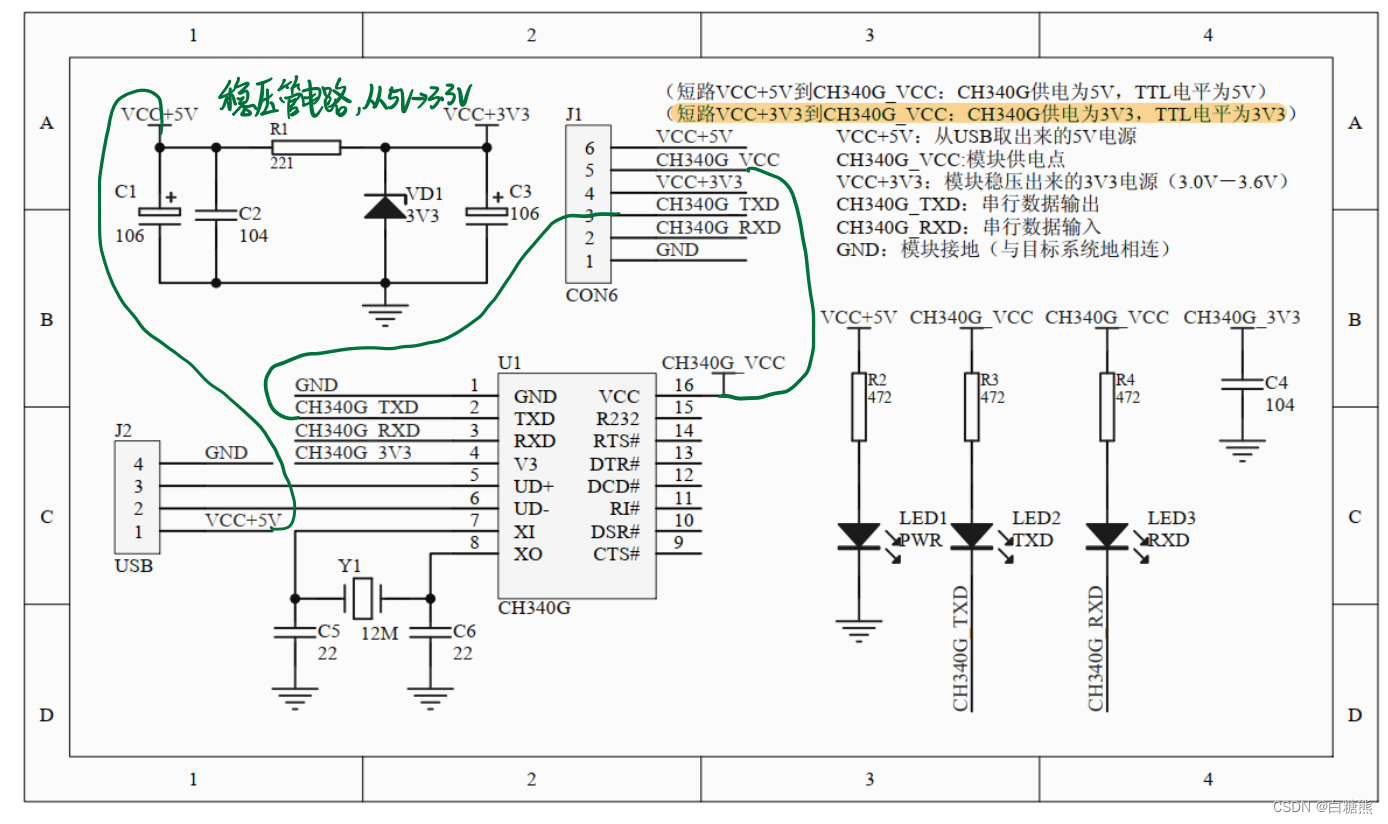
【江科大】STM32:USART串口(理论部分)上
串口 全双工:可以进行同步通信 单端信号:信号线传输的就是单端信号。(也就是与地线(GND)的电势差) 缺点:防干扰能力差 原因:当信号从A点传输到B点,理想条件是A࿰…...

深入了解Linux中常见的五种文件类型
了解文件类型对于正确理解和管理文件系统非常重要。希望本文能够帮助您更好地了解Linux中常见的文件类型及其在ls -l命令输出中的表示方式。 在Linux操作系统中,文件是操作系统中最基本的概念之一。在Linux中,每个文件都有一个特定的类型,这…...

SSM项目集成Spring Security 4.X版本(使用spring-security.xml 配置文件方式)
目录 前言 实战开发: 一、Spring Security整合到SSM项目 1. pom文件引入包 2. web.xml 配置 3. 添加 spring-security.xml 文件 二、Spring Security实战应用 1. 项目结构 2. pom文件引入 3. web.xml 配置 4. Spring 配置 applicationContext.xml 5. sp…...

如何生成开发语言的排名图表
1、解释说明 生成开发语言排名图表,通常需要以下几个步骤: - 首先,我们需要收集一些关于不同编程语言的统计数据,例如使用人数、市场份额等。这些数据可以从各种来源获取,例如网站、报告、数据库等。 - 然后&#x…...
有哪些简单好用、适合中小型企业的CRM系统?
阅读本文,你将了解:一、中小型企业对CRM系统的主要需求;二、盘点四款好用的CRM系统;三、CRM系统实施策略和优秀实践。 在快速变化的商业环境中,中小型企业面临着独特的挑战:如何在有限的资源下高效地管理客…...

Unity 适配器模式(实例详解)
文章目录 简介1. **Input Adapter 示例**2. **Component Adapter 示例**3. **网络数据解析适配器**4. **物理引擎适配**5. **跨平台服务适配** 简介 Unity中的适配器模式(Adapter Pattern)主要用于将一个类的接口转换为另一个接口,以便于原本…...

Spring boot项目java bean和xml互转
Spring boot项目实现java bean和xml互转 项目场景:互转方法使用jackson进行互转使用jaxws进行xml与bean的互转 搞定收工! 项目场景: 工作中需要给下游第三方收费系统做数据挡板,由于下游系统使用的是soap webservice,里面涉及各种…...
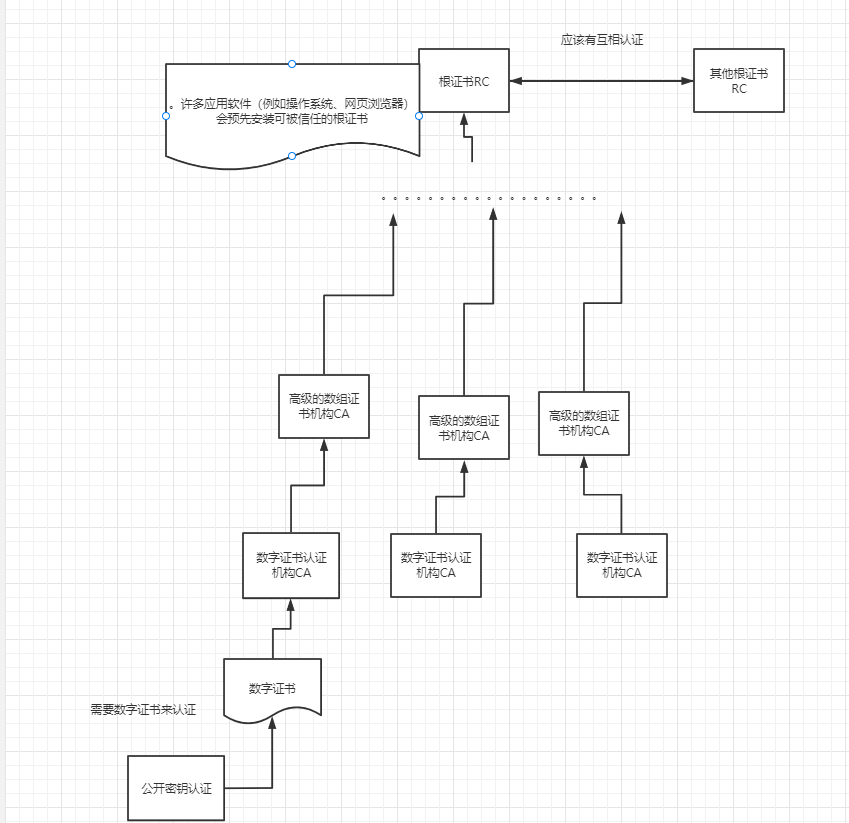
数字证书和数字证书认证机构和数字根证书,CA,RCA
文章目录 一、 数字证书1、什么是数字证书2、数字证书干什么的3、风险 二、数字证书认证机构(Certificate Authority,缩写为CA)参考文章 一、 数字证书 维基百科 公开密钥认证(英语:Public key certificateÿ…...

java web mvc-08-Grails 入门介绍
拓展阅读 Spring Web MVC-00-重学 mvc mvc-01-Model-View-Controller 概览 web mvc-03-JFinal web mvc-04-Apache Wicket web mvc-05-JSF JavaServer Faces web mvc-06-play framework intro web mvc-07-Vaadin web mvc-08-Grails 开源 The jdbc pool for java.(java …...

深度学习技术栈 —— Pytorch之TensorDataset、DataLoader
深度学习技术栈 —— Pytorch之TensorDataset、DataLoader 前言一、TensorDataset、DataLoader的用法?二、从.csv文件-->tensor张量总结 前言 简单来说,TensorDataset与DataLoader这两个类的作用, 就是将数据读入并做整合,以便…...
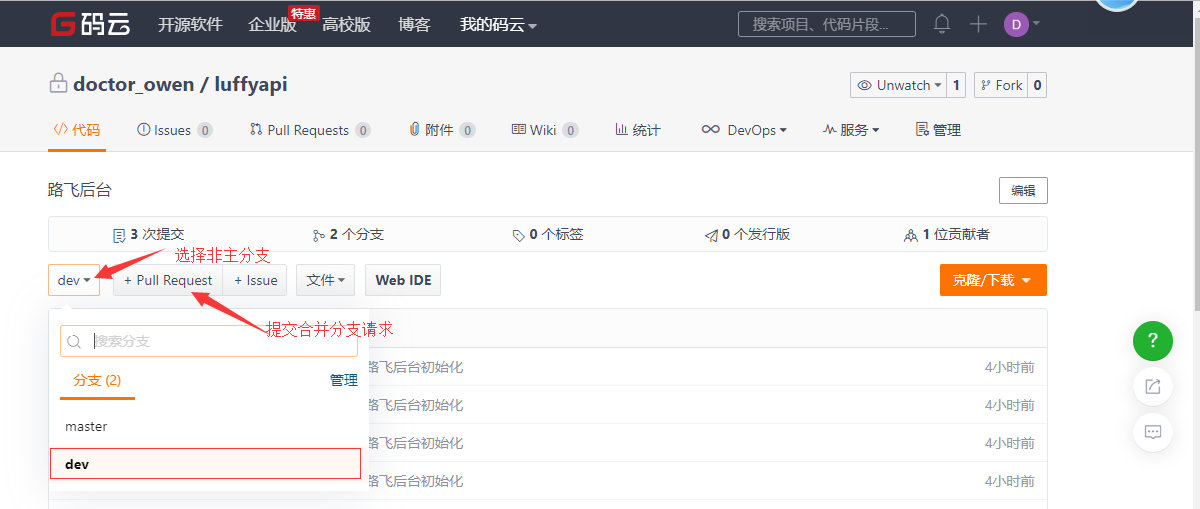
远程git开发
两种本地与远程仓库同步 """ 1)你作为项目仓库初始化人员:线上要创建空仓库 > 本地初始化好仓库 > 建立remote链接(remote add) > 提交本地仓库到远程(push)2)你作为项目后期开发人员:远程项目仓库已经创…...

Codeforces Round 812 (Div. 2) ---- C. Build Permutation --- 题解
目录 C. Build Permutation 题目描述: 编辑 思路解析: 代码实现: C. Build Permutation 题目描述: 思路解析: 先证明在任何情况下答案均存在。 假设我们所求的为 m m1 m2.....n 的排列,我们称不小于n…...
)
Matlab 将工作区变量保存到文件中(save)
语法 1、save(filename) 2、save(filename,variables) 3、save(filename,variables,fmt) 4、save(filename,variables,version) 5、save(filename,variables,version,-nocompression) 6、save(filename,variables,-append) 7、save(filename,variables,-append,-nocompression…...

源码实现简介
本系列所有代码在文章底部,每一章节代码可独立编译运行 随着科技的飞速发展,自动驾驶技术正逐渐成为现实。而在自动驾驶技术中,感知是至关重要的一个环节。通过感知,自动驾驶车辆能够识别和理解周围环境,进而做出相应…...

我每天如何使用 ChatGPT
我们都清楚互联网的运作方式——充斥着各种“爆款观点”,极端分裂的意见,恶搞和无知现象屡见不鲜。 最近,大家对于人工智能(AI)特别是大语言模型(LLMs)和生成式 AI(GenAI࿰…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
