【第十五课】数据结构:堆 (“堆”的介绍+主要操作 / acwing-838堆排序 / 时间复杂度的分析 / c++代码 )
目录
关于堆的一些知识的回顾
数据结构:堆的特点
"down" 和 "up":维护堆的性质
down
up
数据结构:堆的主要操作
acwing-838堆排序
代码如下
时间复杂度分析
确实是在写的过程中频繁回顾了很多关于树的知识,有关的文章都在专栏里,需要的可以去回顾一下~
http://t.csdnimg.cn/0d6Iq![]() http://t.csdnimg.cn/0d6Iq
http://t.csdnimg.cn/0d6Iq
关于堆的一些知识的回顾
关于堆,我的印象中是内存机制里的堆。之前写过的,在回顾一下吧~

然而我们这里说的堆,其实是一种用数据结构中的完全二叉树实现的堆。
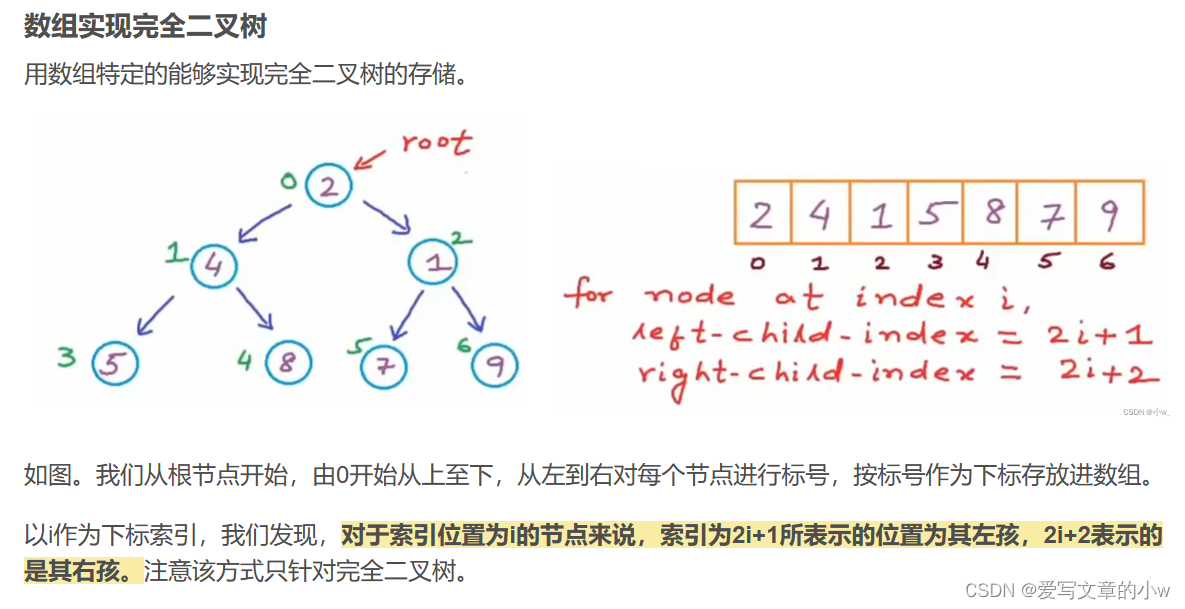
(我们这里图片上写的坐标索引方式是根节点从0开始索引,我们下面会采用下标从1开始索引,那样的话,左儿子就应该是2x 右儿子是2x+1 可以理解哈)
其实这里还要回顾一下树的广度优先遍历,即一层一层,从左到右的遍历方式,对于完全二叉树来说,其广度优先遍历就是创建一个数组,按照特定的存储方式进行存储,最终直接输出数组元素。对于其他的树,采取队列的存储方式。下面这篇文章详细介绍了树的遍历,也对数组存储有更深的解释,感兴趣可以看一下
http://t.csdnimg.cn/NngZ6
数据结构:堆的特点
1.完全二叉树的结构
堆是一个完全二叉树,这意味着除了最底层,其他层都是满的,而最底层的节点都集中在左侧。
到这里就要疑惑为什么堆是完全二叉树这种结构了
http://www.zhihu.com/question/36134980/answer/87490177
这篇文章作者详细解释了关于"堆"这种数据结构好处包括用途,我感觉写的非常不错,可以看一下加深理解。
其中主要提到:1.完全二叉树这种结构可以使用数组实现存储,并且便于索引。
2.它的出现是为了解决----对一个动态的序列进行排序,并且随时想知道这个序列的最小值或最大值
2.最小堆和最大堆
堆可以分为最小堆和最大堆两种类型。在最小堆中,每个节点的值都小于或等于其子节点的值。而在最大堆中,每个节点的值都大于或等于其子节点的值。(也叫小根堆和大根堆)
"down" 和 "up":维护堆的性质
"down" 操作通常涉及到将元素向下移动,适用于删除操作和堆化过程中。
通过 down(k) 进行下沉操作是为了调整以 k 为根的子树,确保其满足最小堆的性质。这主要关注了 k 节点向下的关系。
"up" 操作涉及到将元素向上移动,适用于插入操作和堆化过程中。
通过 up(k) 进行上浮操作是为了确保从删除元素的位置 k 开始,向上到根节点的路径上的每个父节点都满足最小堆的性质。这主要关注了 k 节点向上的关系。
而我们所说的 "down" 和 "up" 是通常用于--维护堆的性质。以确保堆的性质不被破坏。
下面以小根堆为例
down

根据这个思路我们写出代码
//调整以x为根的子树,以满足小根堆的性质(x是经过某种操作得到的值,在操作之前整棵树是满足堆的性质的)
void down(int x)
{int t=x;//t表示三个数中的最小值
//比较的前提都是孩子存在if(x*2<=size && he[x*2]<he[t])t=x*2;if(x*2+1<=size && he[x*2+1]<he[t])t=x*2+1;if(x!=t)//所以这里如果不需要交换位置,那说明更改的这个值并没有破坏原有的性质{swap(he[x],he[t]);down(t);//需要交换 说明我们又更改了一个位置的值,所以要继续判断这次更改的是否符合性质}
}down操作的前提就是 本身这个树的每个节点都是符合性质的,只是某一个值发生了改变,
我们针对这个发生改变的值,不管它是插入还是修改还是更改而导致的值的变化,我们最主要的就是关注改值之后,以其为根节点的子树。
将该值与它的原本的左右两个孩子的值的比较,如果不需要交换位置,说明这次的更改的值并没有引起堆的性质的变化
up
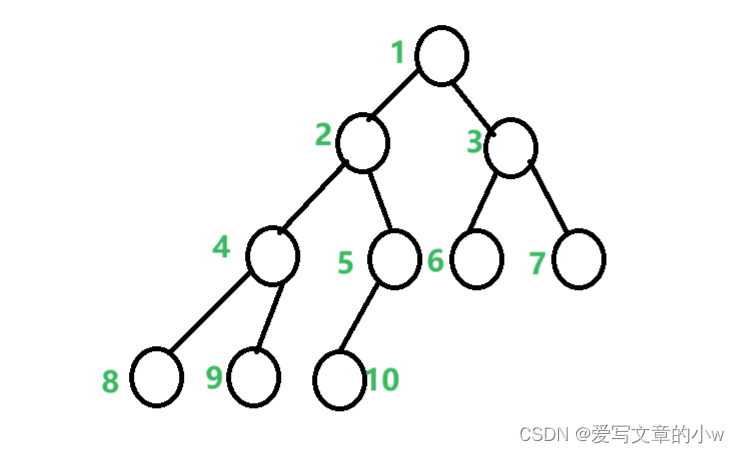
如上图这种完全二叉树,按照数组存储方式,观察其下标表示,我们发现孩子节点是其父节点下标的二倍。
由于小根堆的性质,根节点小于左右孩子,所以我们检查的时候只看该节点与根节点的大小关系就好了,因为另一个孩子一定是大于根节点且符合性质的。
void up(int x)
{while(x/2 && he[x/2]>he[x])//当该元素存在父节点且满足大小关系{swap(he[x/2],he[x]);x /= 2;//更新父节点}
}有了上面down的详细解释这个应该很容易理解了。
数据结构:堆的主要操作
1.插入一个元素,并仍保持堆的性质。
2.删除最小/大值。
3.堆化:将一个无序数组转换为堆,或者修复一个破坏了堆性质的堆。
这里先详细说一下堆化
for(int i=n/2;i;i--)down(i);我们通常从倒数第二层(n/2是最后一个元素的父节点)开始进行逐个元素下沉,最终达到将数组堆化的结果。 这是因为底层节点是叶子节点,它们自身已经满足堆的性质,不需要进行下沉操作。
 关于手写堆的一些主要操作就是上面这些。
关于手写堆的一些主要操作就是上面这些。
下面我逐个来解释。
1.插入一个数。由于我们堆结构是用数组实现存储的完全二叉树,因此对于数组来说,在末尾添加一个元素是很容易的,所以我们先把这个要插入的元素放到堆的末尾,在进行up操作,使其符合堆的性质。
2.求最小值,我们小根堆的根节点就是其最小值。
3.删除最小值。由于我们总是要删除一个元素的,在数组存储结构中,删除最后一个元素是很简单的,直接使我们使用到的下标--就行,但是我们要删的是第一个元素呀,怎么办呢?我们把最后一个元素的值标记覆盖到第一个元素的位置,再删除掉最后一个元素,再把刚刚放到第一位的元素进行down操作,使其符合堆的性质。
4.删除任意一个元素。在3思路的基础上,由于我们不清楚最后一个元素相较于原来这个位置上删除掉的元素是大还是小,如果是大于原来的元素,那就会执行down,如果小于,就会向上执行up,因此,这两个只会执行其中一个,为了简化代码,我们直接不判断,把两个都放上去。
5.修改任意一个元素,解释同4
acwing-838堆排序
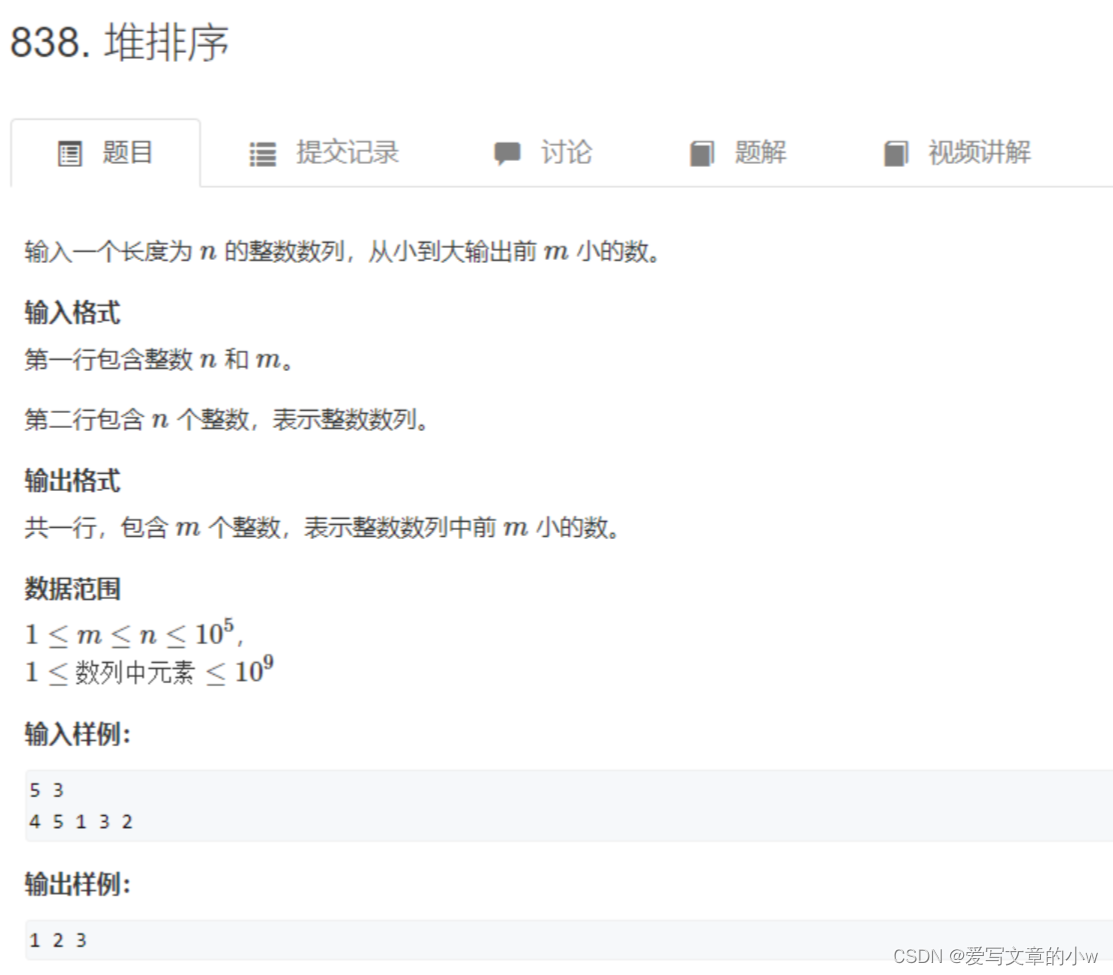
经过上面的介绍其实这道题的核心都已经解了,直接看代码把。
代码如下
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int n,m;
int he[N],size;//调整以 x 为根的子树,以满足小根堆的性质
void down(int x)
{int t=x;//t表示三个数中的最小值if(x*2<=size && he[x*2]<he[t])t=x*2;if(x*2+1<=size && he[x*2+1]<he[t])t=x*2+1;if(x!=t){swap(he[x],he[t]);down(t);}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&he[i]);}size=n;//size标记数组最后一个元素for(int i=n/2;i;i--)down(i);//将数组堆化while(m--)//每次输出一个最小值{printf("%d ",he[1]);he[1]=he[size];//删除最小值size--;down(1);}return 0;
}时间复杂度分析
在这段代码中:
①输入数据的for循环O(n)
②建堆的for循环,先看down函数,down是逐层比较,其时间复杂度取决于树的高度,所以最坏情况下就是该二叉树为满二叉树时的树高,即log(n)。那么整个建堆过程时间复杂度应为O(n*log(n))
关于这种说法其实是错误的,表面上看好像是这样,但是这个观点没有考虑到在建堆过程中,每个节点的调整代价并不都是logn,因为我们这里采用的是自下而上的弗洛伊德建堆方式,使用的是down函数,其最坏时间复杂度也是O(n)。
关于它是如何得出的?下面这些文章都写得很好很清楚,可以帮助大家理解。
建堆分为从上向下建和从下向上建。
【数据结构】堆的建立 (时间复杂度计算-堆排序)---超细致-阿里云开发者社区 (aliyun.com)
这篇文章前半部分通过图示和公式计算详细的解释了这两种建堆方式的时间复杂度,写得很
好,容易理解。大家可以看他写的。
堆排序中建堆过程时间复杂度O(n)怎么来的?
在堆排序中,无论是使用大根堆还是小根堆,其实都可以达到排序的目的,只是排序的顺序不同。想得到升序序列倾向建立大根堆,想得到降序序列倾向建立小根堆。
③输出最小值的while循环,也是取决于down函数执行次数,即O(m*log(n))
在小根堆中,只有根节点是最小的,但是其下的两个节点之间大小关系不一定是升序。当我们需要获取前m小的数时,我们需要做的是利用while循环反复取出根节点(也就是当前堆中的最小值),然后进行堆调整,以保证剩下的部分仍然满足小根堆的性质。
所以总的时间复杂度,最坏情况下应该是O(n+n+n*logn)=O(n*logn),第一个n代表读入数据,第二个n代表弗洛伊德方式建堆,第三个n*logn代表每次移除根节点之后的堆调整
哎,就差一个模拟堆(烦躁),是有点强迫症在的😢明天在写啦。。
有问题欢迎指出!一起加油!!
相关文章:

【第十五课】数据结构:堆 (“堆”的介绍+主要操作 / acwing-838堆排序 / 时间复杂度的分析 / c++代码 )
目录 关于堆的一些知识的回顾 数据结构:堆的特点 "down" 和 "up":维护堆的性质 down up 数据结构:堆的主要操作 acwing-838堆排序 代码如下 时间复杂度分析 确实是在写的过程中频繁回顾了很多关于树的知识&…...

el-select选项过多导致页面卡顿,路由跳转卡顿
问题:el-select数据量太大,导致渲染过慢,或造成页面卡顿甚至于卡死 卡顿原因:DOM中数据过多,超过内存限制 解决方法: 1.使用Virtualized Select 虚拟化选择器,页面就不卡了 2.el-select做分…...

信息流广告参数回传工具怎么做联调
信息流广告在抖音等平台上越来越受到广告主的青睐,它能够在用户浏览内容的同时,以自然的方式展示广告,提高曝光率和点击率。然而,为了更好地评估广告效果,需要进行参数回传联调。本文将介绍一种实用的工具——数灵通外…...

matlab appdesigner系列-常用18-表格
表格,常用来导入外部表格数据 示例: 导入外界excel数据:data.xlsx 姓名年龄城市王一18长沙王二21上海王三56武汉王四47北京王五88成都王六23长春 操作步骤如下: 1)将表格拖拽到画布上 2)对app1右键进行…...
密码学的100个基本概念
密码学作为信息安全的基础,极为重要,本文分为上下两部分,总计10个章节,回顾了密码学的100个基本概念,供小伙伴们学习参考。本文将先介绍前五个章节的内容。 一、密码学历史 二、密码学基础 三、分组密码 四、序列密码 五、哈希…...

Python中的进制转换——bin/oct/hex函数与int函数
简介 进制转换可能是一个工作学习中的常见小任务,手写相关函数显然很麻烦。 Python有相关内置函数一般能满足我们的需求。bin()、oct()、hex()将十进制转换为常用的二、八、十六进制,而 int()函数可指定第二个参数从而将其它进制转换为十进制。或许后者…...
RT-Thread 瑞萨 智能家居网络开发:RA6M3 HMI Board 以太网+GUI技术实践
不用放大了, 我在包里找到张不小的…… 以太网HMI线下培训-环境准备 这是社群的文档:【腾讯文档】以太网线下培训(HMI-Board) https://docs.qq.com/doc/DY0FIWFVuTEpORlNn 先介绍周六的培训是啥,然后再介绍一下要准…...

力扣刷题第十天 美丽塔 一
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。 你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。 如果以下条件满足,我们称这些塔是 美丽 的: 1 < heights[i] < maxHeights[i]heights 是一个 山脉…...

c# ADODB.Recordset实例调用Fields报错
代码: using System; using System.CodeDom; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using ADODB;namespace ConsoleApp1 {internal class Programre{static ADODB.Recordset recordsetInstance…...
windows和linux下SHA1,MD5,SHA256校验办法
今天更新android studio到Android Studio Hedgehog | 2023.1.1时,发现提示本机安装的git版本太老,于是从git官网下载最新的git。 git下载地址: https://git-scm.com/ 从官网点击下载最新windows版本会跳转到github仓库来下载发布的git&…...

高新技术企业申报需要具备哪些条件?
(一)企业申请认定时须注册成立一年以上; (二)企业通过自主研发、受让、受赠、并购等方式,获得对其主要产品(服务)在技术上发挥核心支持作用的知识产权的所有权; &#…...

测试不拘一格——掌握Pytest插件pytest-random-order
在测试领域,测试用例的执行顺序往往是一个重要的考虑因素。Pytest插件 pytest-random-order 提供了一种有趣且灵活的方式,让你的测试用例能够以随机顺序执行。本文将深入介绍 pytest-random-order 插件的基本用法和实际案例,助你摆脱固定的测试顺序,让测试更具变化和全面性…...
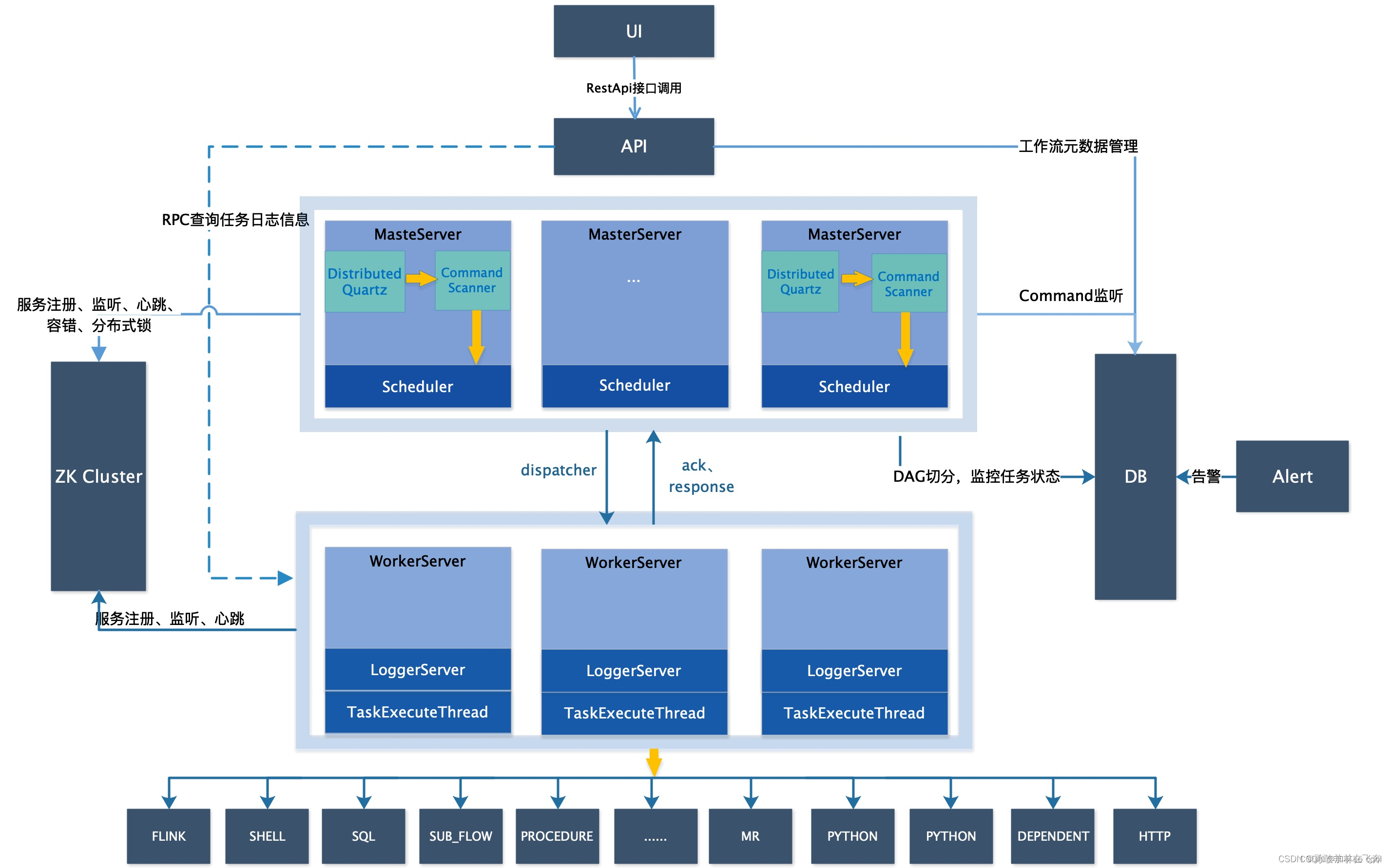
DophineScheduler通俗版
1.DophineScheduler的架构 ZooKeeper: AlertServer: UI: ApiServer: 一个租户下可以有多个用户;一个用户可以有多个项目一个项目可以有多个工作流定义,每个工作流定义只属于一个项目;一个租户可…...

企业如何稳步开启SASE实施之路
在上一篇题为《企业为什么选择SASE?香港电讯专家给你答案!》的文章中,我们从SD-WAN的安全策略和能力、市场趋势的推动及SASE的四大特性分析了企业选择采用安全访问服务边缘(SASE)的原因。基于SASE的各项优势࿰…...
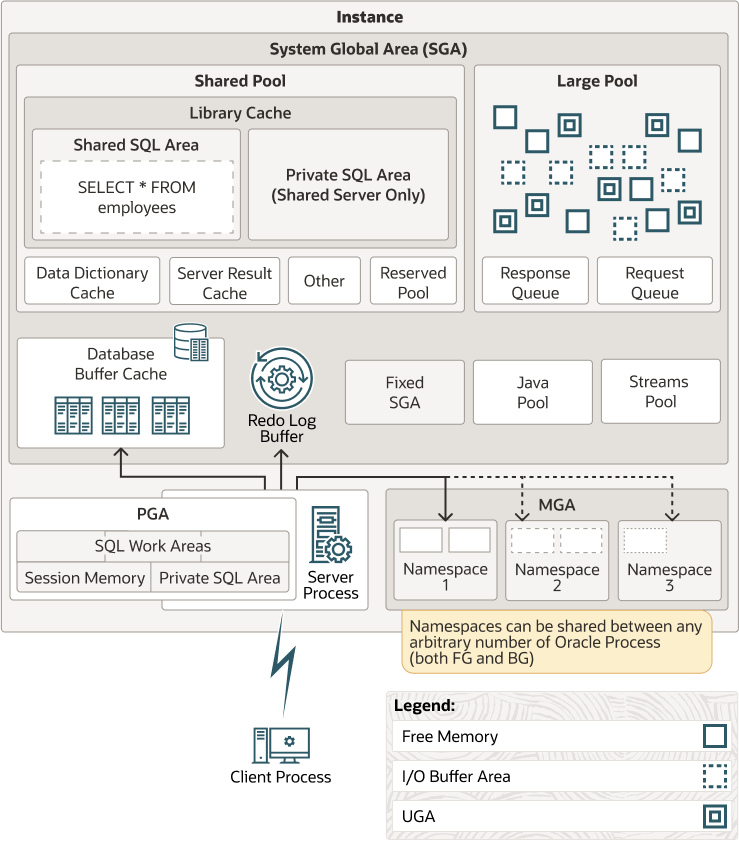
【Oracle】收集Oracle数据库内存相关的信息
文章目录 【Oracle】收集Oracle数据库内存相关的信息收集Oracle数据库内存命令例各命令的解释输出结果例参考 【声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和数据库技术(ID:SQLplusDB) 【Oracle】收集Oracle数据库内存相关的信息 …...

MySQL也开始支持JavaScript了
2023 年 12 月 16 日,Oracle 公司在一篇名为 《Introducing JavaScript support in MySQL》的文章中宣布 MySQL 数据库服务器将开始支持 JavaScript 语言。 这个举措标志着继PostgreSQL之后, MySQL 也支持使用 JavaScript 编写函数和存储过程了。作为最…...

百度大脑 使用
百度大脑: 官方网址:https://ai.baidu.com/ 文档中心:https://ai.baidu.com/ai-doc 体验中心:https://ai.baidu.com/experience 百度大脑则是百度AI核心技术引擎,它包括基础层、感知层、认知层和安全,是百…...
Spring Boot 中的外部化配置
Spring Boot 中的外部化配置 一、配置文件基础1.配置文件格式(1)YAML 基本语法规则(2)YAML 支持三种数据结构 2.application 文件3.application.properties 配置文件4.application.yml 配置文件5.Environment6.组织多文件7.多环境…...

10个常考的前端手写题,你全都会吗?(下)
前言 📫 大家好,我是南木元元,热爱技术和分享,欢迎大家交流,一起学习进步! 🍅 个人主页:南木元元 今天接着上篇再来分享一下10个常见的JavaScript手写功能。 目录 1.实现继承 ES5继…...

Java 面试题库
基础篇 面向对象的特征 封装(Encapsulation): 封装是指将对象的数据(属性)和行为(方法)结合在一起,形成一个独立的实体。对象的数据被隐藏在内部,只能通过定义好的接口&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
