【rust/bevy】使用points构造ConvexMesh
目录
- 说在前面
- 问题提出
- Rapier
- 具体实现
- 参考
说在前面
- 操作系统:win11
- rust版本:rustc 1.77.0-nightly
- bevy版本:0.12
- github:这里
问题提出
-
在
three.js中,可以通过使用ConvexGeometry从给定的三维点集合生成凸包(Convex Hull)import { ConvexGeometry } from 'three/addons/geometries/ConvexGeometry.js';例如:
const geometry = new ConvexGeometry( points ); const material = new THREE.MeshBasicMaterial( { color: 0x00ff00 } ); const mesh = new THREE.Mesh( geometry, material ); scene.add( mesh );
-
但是在
bevy中如何实现呢?
Rapier
- 在当前
bevy的版本中,并没有类似的实现,目前支持的shape也比three.js少:- Box
- Capsule
- Circle
- Cube
- Cylinder
- Icosphere
- Plane
- Quad
- RegularPolygon
- Torus
- UVSphere
- 所以,如果要构造
ConvexHull,只能借助第三方库(或者自己实现,可以参考three.js实现) - 这里我们借助一个物理库
rapier来实现 - 关于rapier
这里
具体实现
-
首先我们通过点集构造
ConvexHull,rapier可以直接完成这一步:let collider = Collider::convex_hull(&points);但是该方法构造的是一个
Collider,实际上是无法直接当成Mesh使用的 -
然后我们将其转换成
ConvexPolyhedronlet convex = c.as_convex_polyhedron().unwrap(); -
该结构中包含一个凸包的所有属性,例如点、边、面等,事实上,它提供了一个方法,能够直接转换成TriangleMesh所需要的数据:
impl ConvexPolyhedron {/// Discretize the boundary of this convex polyhedron as a triangle-mesh.pub fn to_trimesh(&self) -> (Vec<Point3<Real>>, Vec<[u32; 3]>) {let mut indices = Vec::new();for face in self.faces() {let i1 = face.first_vertex_or_edge;let i2 = i1 + face.num_vertices_or_edges;let first_id = self.vertices_adj_to_face()[i1 as usize] as u32;for idx in self.vertices_adj_to_face()[i1 as usize + 1..i2 as usize].windows(2) {indices.push([first_id, idx[0] as u32, idx[1] as u32]);}}(self.points().to_vec(), indices)} }但是不包含
normal数据,导致光照对其没有作用

-
所以我们需要自己实现一个相似的方法,首先我们来看看测试数据,实际上它有20个点,共12个面,每个面是一个正五边形,所以使用TriangleMesh来表达的话,一共是36个三角形
-
再让我们来看看
bevy中构造一个TriangleMesh需要哪些数据:fn create_simple_parallelogram() -> Mesh {// Create a new mesh using a triangle list topology, where each set of 3 vertices composes a triangle.Mesh::new(PrimitiveTopology::TriangleList)// 顶点数据.with_inserted_attribute(Mesh::ATTRIBUTE_POSITION,vec![[0.0, 0.0, 0.0], [1.0, 2.0, 0.0], [2.0, 2.0, 0.0], [1.0, 0.0, 0.0]])// uv数据 在本文中我们并不需要.with_inserted_attribute(Mesh::ATTRIBUTE_UV_0,vec![[0.0, 1.0], [0.5, 0.0], [1.0, 0.0], [0.5, 1.0]])// 法线.with_inserted_attribute(Mesh::ATTRIBUTE_NORMAL,vec![[0.0, 0.0, 1.0], [0.0, 0.0, 1.0], [0.0, 0.0, 1.0], [0.0, 0.0, 1.0]])// 三角形的顶点索引.with_indices(Some(Indices::U32(vec![0, 3, 1,1, 3, 2]))) } -
对比我们需要的数据,以及
to_trimesh方法,发现我们少了normal数据,不过这个数据在face中就有,那么所有条件就具备了 -
完整代码
let plist: Vec<f32> = vec![0., 3.568220853805542, 9.341723442077637, 5.773502826690674, 5.773502826690674, 5.773502826690674, -5.773502826690674, 5.773502826690674, 5.773502826690674, 3.568220853805542, 9.341723442077637, 0., -3.568220853805542, 9.341723442077637, 0., 9.341723442077637, 0., 3.568220853805542, 9.341723442077637, 0., -3.568220853805542, 5.773502826690674, 5.773502826690674, -5.773502826690674, 5.773502826690674, -5.773502826690674, -5.773502826690674, 0., -3.568220853805542, -9.341723442077637, 0., 3.568220853805542, -9.341723442077637, -5.773502826690674, -5.773502826690674, -5.773502826690674, -9.341723442077637, 0., -3.568220853805542, -5.773502826690674, 5.773502826690674, -5.773502826690674, -3.568220853805542, -9.341723442077637, 0., -5.773502826690674, -5.773502826690674, 5.773502826690674, -9.341723442077637, 0., 3.568220853805542, 0., -3.568220853805542, 9.341723442077637, 3.568220853805542, -9.341723442077637, 0., 5.773502826690674, -5.773502826690674, 5.773502826690674]; let points: Vec<Vec3> = plist.array_chunks().into_iter().map(|&v: &[f32; 3]| Vec3::from_array(v)).collect(); // 通过点集构造convex hull let collider = Collider::convex_hull(&points); if let Some(c) = collider {let convex = c.as_convex_polyhedron().unwrap();// 取convex hull的所有面let faces = convex.raw.faces();// 取点集let points = convex.raw.points();// 取映射关系let face_to_vertices = convex.raw.vertices_adj_to_face();let mut positions = Vec::new();// 法向量 用于处理光照let mut normals = Vec::new();let mut indices = Vec::new();// 遍历所有的面for face in faces {let i1 = face.first_vertex_or_edge;let i2 = i1 + face.num_vertices_or_edges;for idx in i1..i2 {let point = points[face_to_vertices[idx as usize] as usize];// 重新构造点集 points是原始点集positions.push([point.x, point.y, point.z]);// 面上的所有点的朝向与面相同normals.push([face.normal.x, face.normal.y, face.normal.z]);}for idx in i1 + 1..i2 - 1 {// 构造顶点索引indices.push([i1, idx as u32, idx + 1 as u32]);}}// 构造Meshlet mesh = Mesh::new(PrimitiveTopology::TriangleList).with_inserted_attribute(Mesh::ATTRIBUTE_POSITION, positions).with_inserted_attribute(Mesh::ATTRIBUTE_NORMAL, normals).with_indices(Some(Indices::U32(indices.concat())));commands.spawn(PbrBundle {mesh: meshes.add(mesh),material: materials.add(Color::rgb_u8(124, 144, 255).into()),transform: Transform::from_xyz(0.0, 1., 0.0).with_scale(Vec3::new(0.1, 0.1, 0.1)),..default()}); } -
结果(gif)

参考
- ConvexGeometry
相关文章:

【rust/bevy】使用points构造ConvexMesh
目录 说在前面问题提出Rapier具体实现参考 说在前面 操作系统:win11rust版本:rustc 1.77.0-nightlybevy版本:0.12github:这里 问题提出 在three.js中,可以通过使用ConvexGeometry从给定的三维点集合生成凸包(Convex Hu…...

【C语言】string.h——主要函数总结
string.h主要定义了字符串处理函数和内存操作函数。 字符串处理函数 strlen() 功能:strlen()函数返回字符串的字节长度,不包括末尾的空字符\0。 函数原型:size_t strlen(const char* s); 返回值:返回的是size_t类型的无符号整…...

如何在前端优化中减少页面加载时间?
在前端优化中,减少页面加载时间是至关重要的,因为快速加载的页面可以提高用户体验,减少跳出率,从而提升网站的整体性能。本文将介绍一些实用的前端优化技巧,以帮助您减少页面加载时间。 一、优化图片 图片是页面加载…...

Typecho后台无法登录显示503 service unavailable问题及处理
一、Typecho 我的博客地址:https://www.aomanhao.top 使用老薛主机动态Typecho博客框架handsome主题的搭配,文章内容可以异地网页更新,可以听后台背景音乐,很好的满足我的痛点需求,博客部署在云端服务器访问响应较快…...

Python入门(一)
anaconda安装 官网:https://www.anaconda.com下载 jupyter lab 简介: 包含了Jupyter Notebook所有功能。 JupyterLab作为一种基于web的集成开发环境,你可以使用它编写notebook,操作终端,编辑markdown文本…...
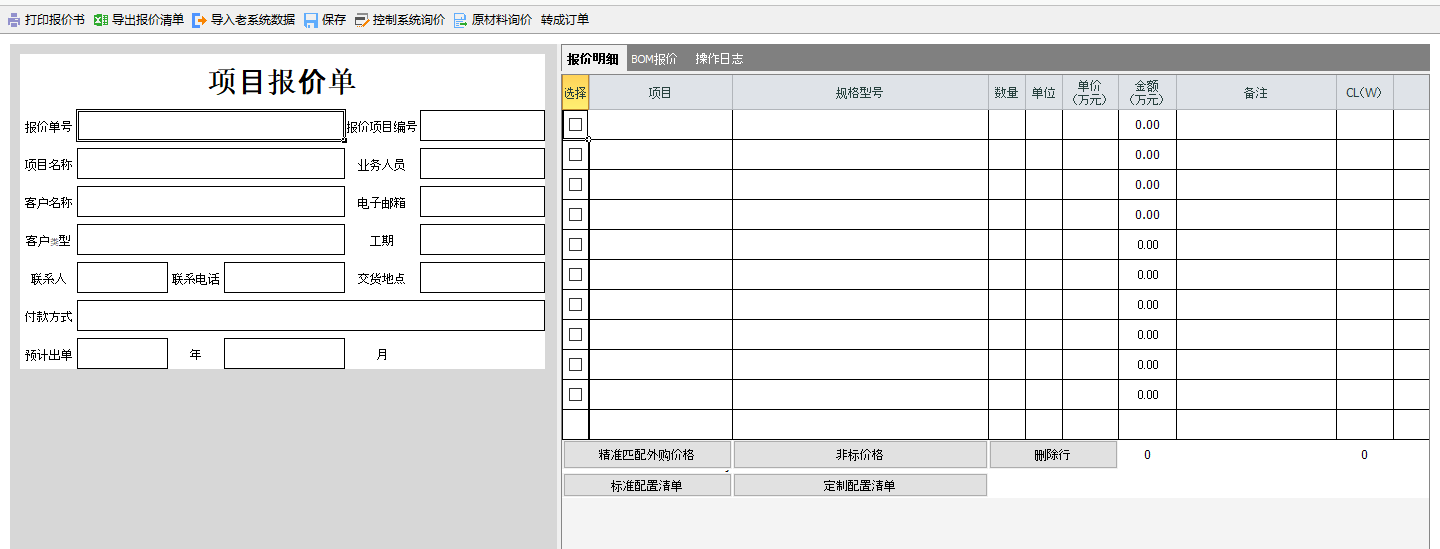
云表企业级无代码案例-自主开发ERP管理系统
痛点 我是一名企业经营者,同时也是信息化建设的坚定倡导者。凭借管理专业背景,我深知经营数据对于企业的至关重要性。如何高效搜集、精准分析经营数据,并将其转化为决策依据,直接关乎企业的生死存亡。太多因盲目决策而倒闭的企业…...
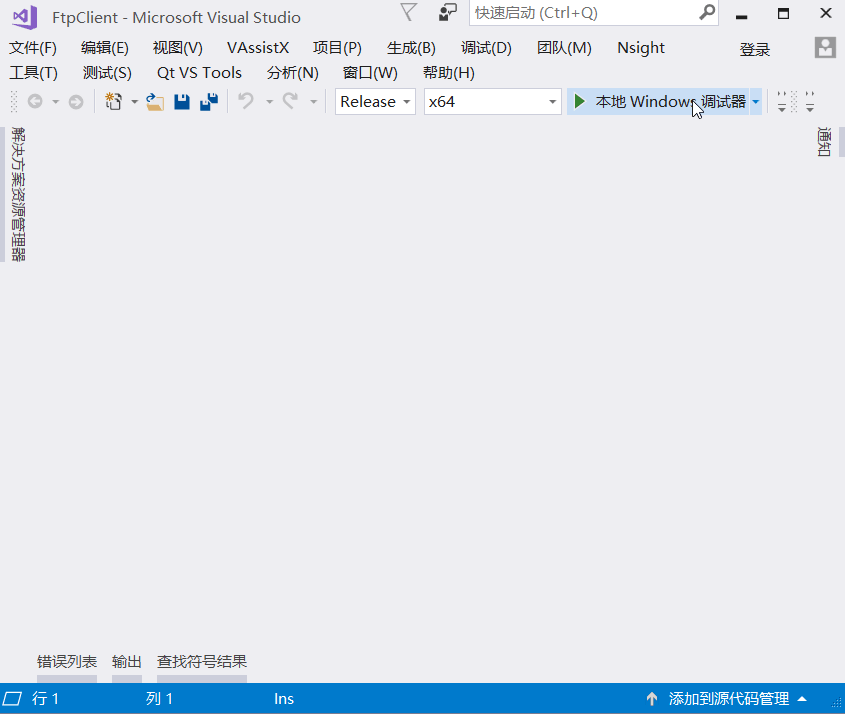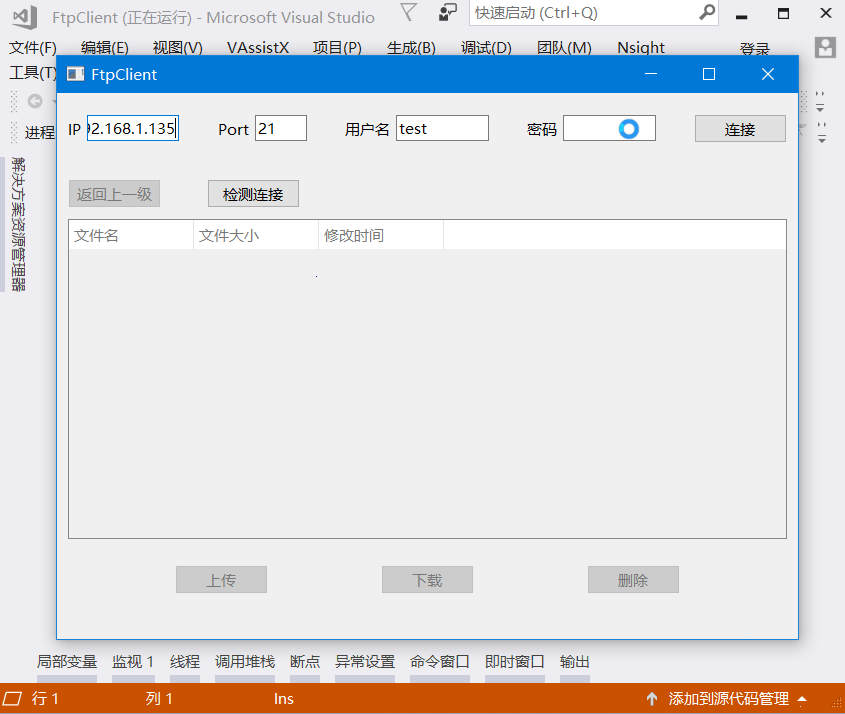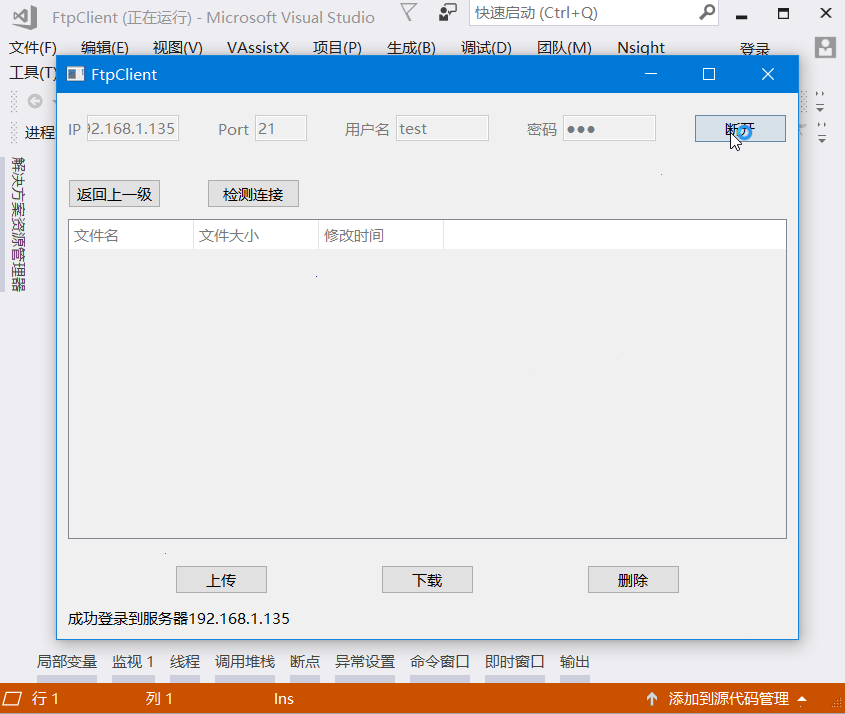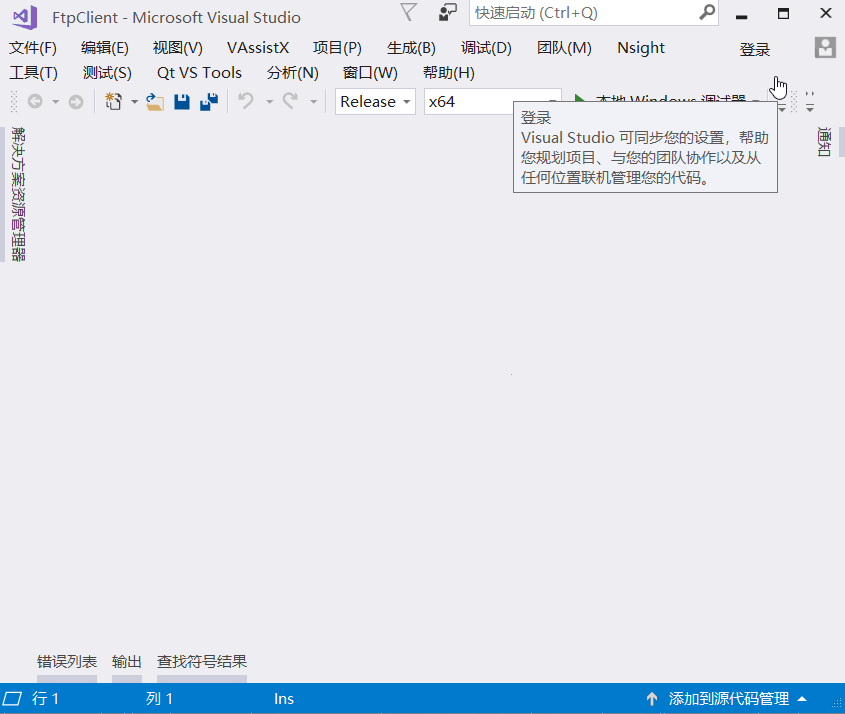
Qt —— 编译Qt5版本QFTP库,并实现连接服务、获取列表、上传、下载、删除文件等操作(附源码、附基于Qt5编译好的QFTP库)
示例效果1 示例效果2 介绍 QFTP是Qt4的库,Qt5改用了QNetworkAccessManager来代替。但是Qt5提供的QNetworkAccessManager仅支持FTP的上传和下载,所以只能将QFTP库编译为Qt5的库来进行调用。 QFTP在Github的下载地址:https://github.com/qt/qtftp 客户端源码生成的release结果…...
碰到es6的...拓展运算符
第一次碰到,哥们啥也不会 let searchForm ref({}) let formData ref({}) const initArgs async() > { args.value props.init_data formData .value { ...searchForm.value,//把值都带过来 workWhere : args.value.workWhere, statusArgs : args.value.sta…...

JDK8新特性详解
☆* o(≧▽≦)o *☆嗨~我是小奥🍹 📄📄📄个人博客:小奥的博客 📄📄📄CSDN:个人CSDN 📙📙📙Github:传送门 📅&a…...
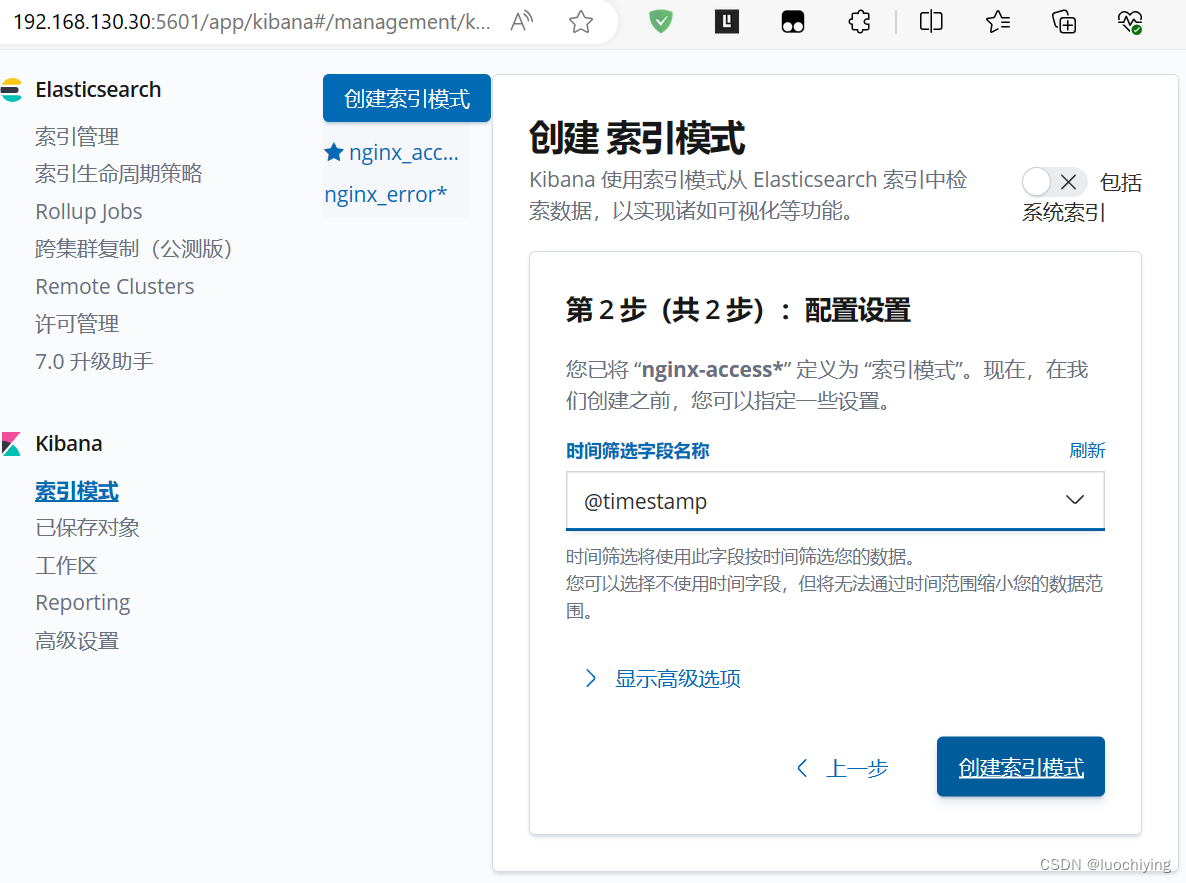
ELK+Filebeat 部署实验
Filebeat是轻量级的开源日志文件数据搜集器。通常在需要采集数据的客户端安装 Filebeat,并指定目录与日志格式,Filebeat 就能快速收集数据,并发送给 logstash 进行解析,或是直接发给 Elasticsearch 存储,性能上相比运行…...

利用wireshark lua扩展能力增加自定义解析器[注释解读版]
前言 Wireshark提供了lua扩展能力,可以定制一些Listner和Dissector,用于一些自定义的使用场景,例如: lua插件适应场景Listener报文统计、内容抽取等Dissector协议树解析,在wireshark中立等可看 已在以前的文档中积累了对于List…...

GPT-5不叫GPT-5?下一代模型会有哪些新功能?
OpenAI首席执行官奥特曼在上周三达沃斯论坛接受媒体采访时表示,他现在的首要任务就是推出下一代大模型,这款模型不一定会命名GPT-5。虽然GPT-5的商标早已经注册。 如果GPT-4目前解决了人类任务的10%,GPT-5应该是15%或者20%。 OpenAI从去年开…...
2024.1.23(347.前k个高频元素)
2024.1.23(347.前k个高频元素) 思路 这道题目主要涉及到如下三块内容: 1.要统计元素出现频率 2.对频率排序 3.找出前K个高频元素 首先统计元素出现的频率,这一类的问题可以使用map来进行统计。 然后是对频率进行排序,这里我们可以使用一种…...

MySQL对数据库的操作
前腰:本节只是的数据库本身进行增删查改、备份、恢复等操作,而不是对数据库内的数据表做操作,还请您区分好这两点。 1.创建数据库 # 创建数据库的语法形式 CREATE DATABASE [IF NOT EXISTS] database_name [create_specification]# 大写的是…...

解决Unity WebGLInput插件全屏输入的问题
unity webgl的中文输入插件WebglInput在全屏的时候会出现无法输入中文/输入的英文会字母出现在光标后面/什么都输入不了的等无法正常使用的情况。 插件官网作者给出了unity的2017,2018,2019版本的全屏输入解决方法。 最新插件下载地址:http…...

Android14实战:调整A2DP音量曲线(五十三)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒体系统工程师系列【原创干货持续更新中……】🚀 人生格言: 人生从来没有捷径,只…...
vector讲解
在学习玩string后我们开始学习vector,本篇博客将对vector进行简单的介绍,还会对vector一些常用的函数进行讲解 vector的介绍 实际上vector就是一个数组的数据结构,但是vector是由C编写而成的,他和数组也有本质上的区别ÿ…...
nvm 配置淘宝镜像失效,以及安装node后 npm-v 无效
win11 nvm版本 1.1.4 和1.1.7和1.1.12(目前最新版本24年 一月二十三日) 以上nvm版本都会出现一下问题, 从https://github.com/coreybutler/nvm-windows/releases 下载nvm安装包如下图 傻瓜式安装后,不用去配置环境变量&#…...
【Android Gradle 插件】Gradle 基础配置 ④ ( Gradle Wrapper 配置作用 | Gradle 下载的依赖库存放位置 )
一、Gradle Wrapper 配置作用 gradle wrapperdistributionBaseGRADLE_USER_HOME distributionPathwrapper/dists distributionUrlhttps\://services.gradle.org/distributions/gradle-6.7.1-bin.zip zipStoreBaseGRADLE_USER_HOME zipStorePathwrapper/distsGradle Wrapper 配…...

Deepin_Ubuntu_查看树形目录结构(tree)
Linux系统(Deepin、Ubuntu)中,可以使用tree命令来查看树形目录结构,下面是一些示例: 查看当前目录的树形结构: tree查看指定目录的树形结构,例如/etc/X11/fonts目录: tree /etc/X…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
