代码随想录刷题笔记 DAY12 | 二叉树的理论基础 | 二叉树的三种递归遍历 | 二叉树的非递归遍历 | 二叉树的广度优先搜索
Day 12
01. 二叉树的理论基础
1.1 二叉树的种类
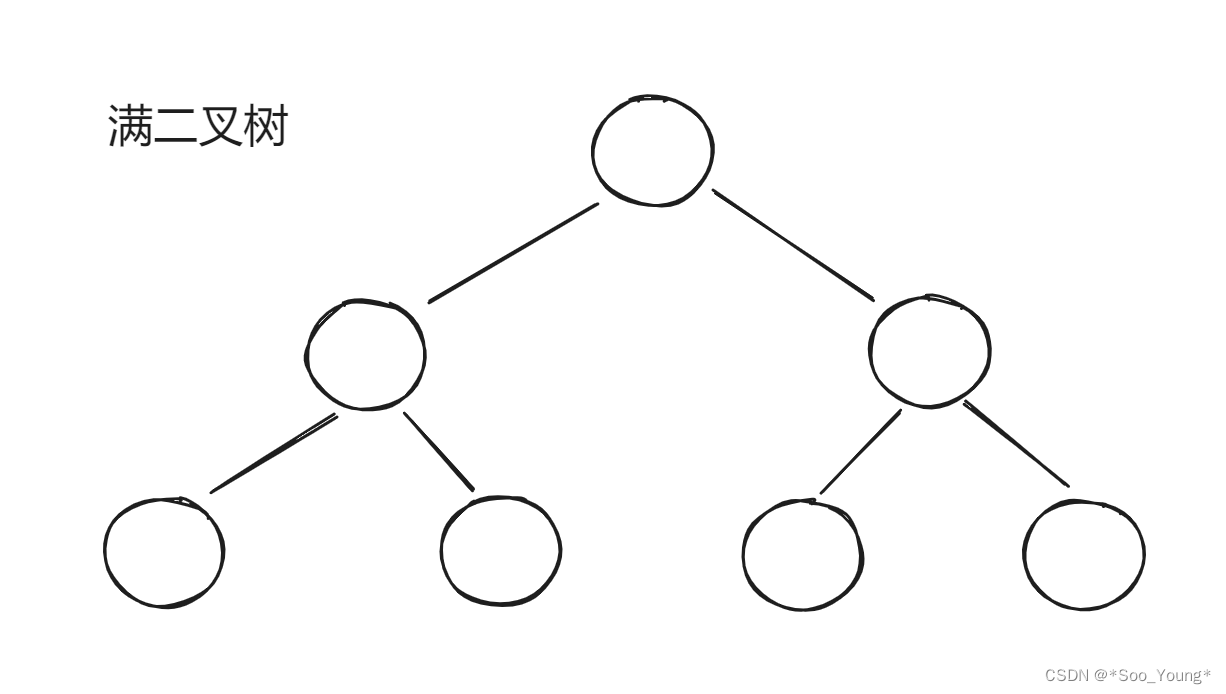
- 满二叉树:除了叶子节点以外,每个节点都有两个子节点,整个树是被完全填满的
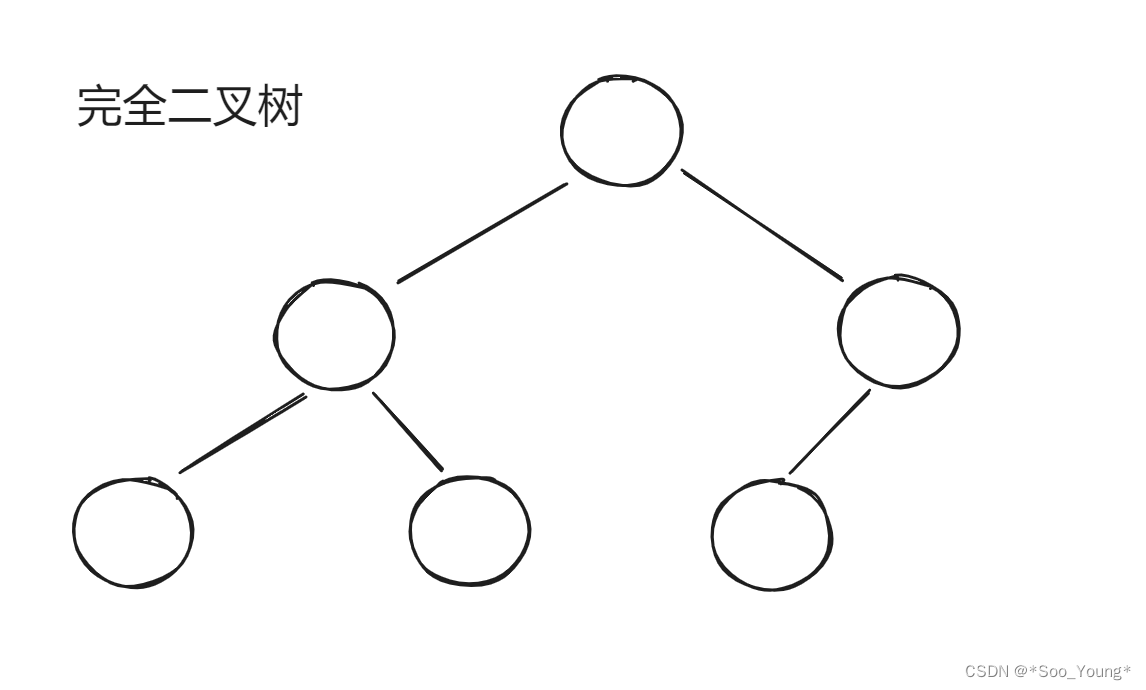
- 完全二叉树:除了底层以外,其他部分是满的,底部可以不是满的但是必须是从左到右连续的

- 二叉搜索树:节点是有顺序的,可查找的
- 平衡二叉搜索树:左子树和右子树的高度值不能超过 1
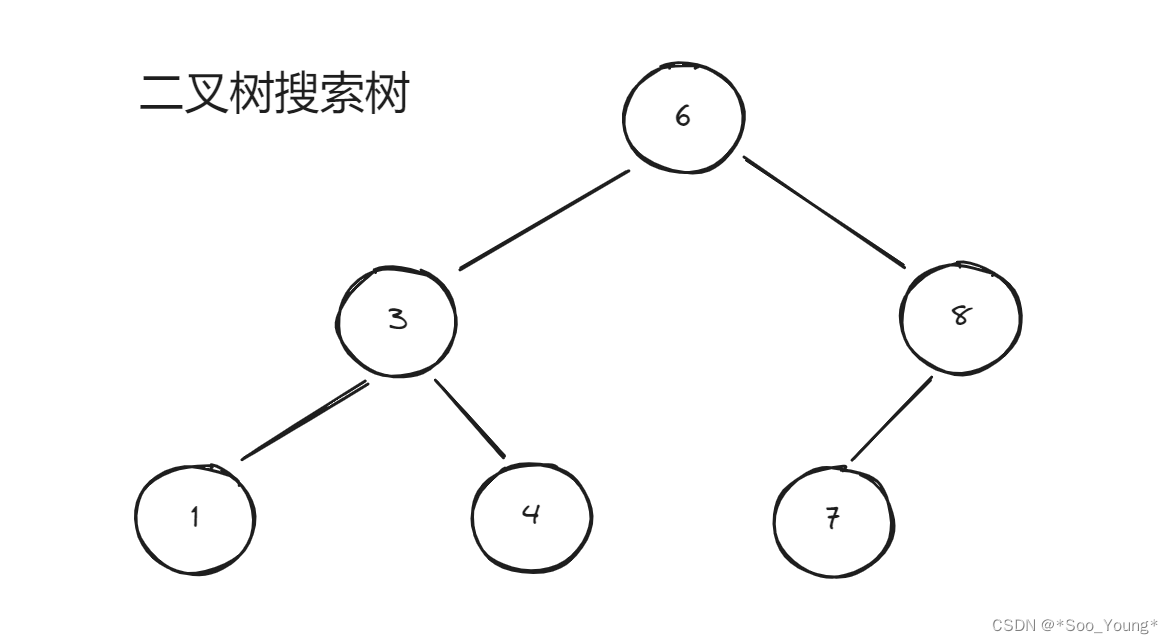
比如上面的树,比 6 大的在左边,小的在右边,且每个节点都是这样的,有顺序的,查询时间复杂度为 logn
很显然我们中间节点的选择会影响左子树和右子树的高度,左子树和右子树高度不超过 1 的被称为平衡二叉搜索树。
1.2 二叉树的存储方式
链式存储:顺序存储即采用链表的方式来存储,是我们常用的存储方式,即使用链表的方式来存储:一个树节点分别有它的左节点和右节点,他们的左节点和右节点又连接着其他的树节点。
顺序存储(了解即可):
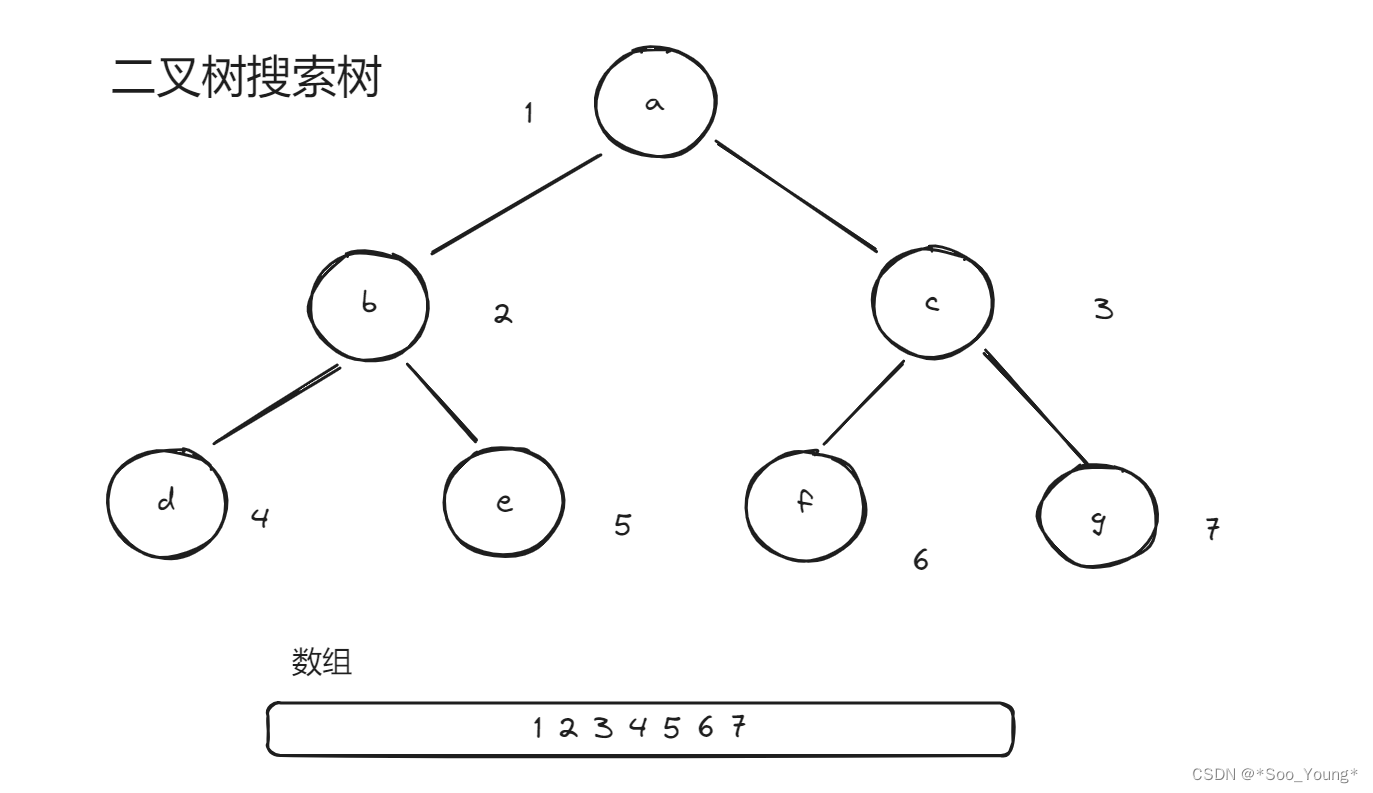
我们给每个节点编号,节点的左节点就是 2n 右节点就是 2n - 1
1.3 遍历方式
深度优先搜索:即先一路搜索到最底部再递归返回,我们常见的前序、中序、后序遍历都是深度优先搜索。
可以使用递归的方式和非递归的方式,迭代的方式有可能在面试中会考察
广度优先搜索:一层一层的去遍历,使用队列先进先出的特性实现广度优先搜索。
1.4 定义方式
class TreeNode {int val;TreeNode rightNode;TreeNode leftNode;
}
和我们上面说的相同,和链表的定义方式相同,但分为左子树和右子树。
02. 二叉树的递归遍历
这一部分应该是很多朋友一开始学算法十分困惑的一个点,总是想不明白递归的题也看不明白递归的解法,我大一刚开始刷算法的时候也是这样,当时真是一入递归深似海,之后有一篇文章启发了我
东哥带你刷二叉树(纲领篇)
拉不拉东老师的这篇关于二叉树文章。
我来借用一下里面的思维方式
我们之所以无法理解递归是因为我们还是利用之前读代码和写代码的方式:“将自己的脑子当作计算机来执行一遍代码”,这在前面那些简单的顺序结构的题目中当然是可行而且有效的,但当我们解决的题目复杂起来,就比如现在的二叉树遍历的题目,我们的脑子能装下几个栈呢?能跑几层递归呢?
所谓理解和读懂递归就是要将它当作自己编写代码、解决问题的一种工具,而不是尝试去用脑子执行它,弄懂它的执行步骤,我们先来看一段二叉树 前序 遍历的代码
class Solution {List<Integer> res = new ArrayList();public List<Integer> preorderTraversal(TreeNode root) {reverse(root);return res;}public void reverse(TreeNode root) {if (root == null) {return;}res.add(root.val);reverse(root.left);reverse(root.right);}
}
我们将重点放在第二段的代码上,如果单单的问你我不看递归,我这一次做了什么?
- 首先我先判断当前的节点是否为空节点,这就是我们常说的递归的出口
- 然后我们将当前节点的值放到了
res的list中作为结果 - 然后我们去递归遍历左子树
- 然后我们去递归遍历右子树
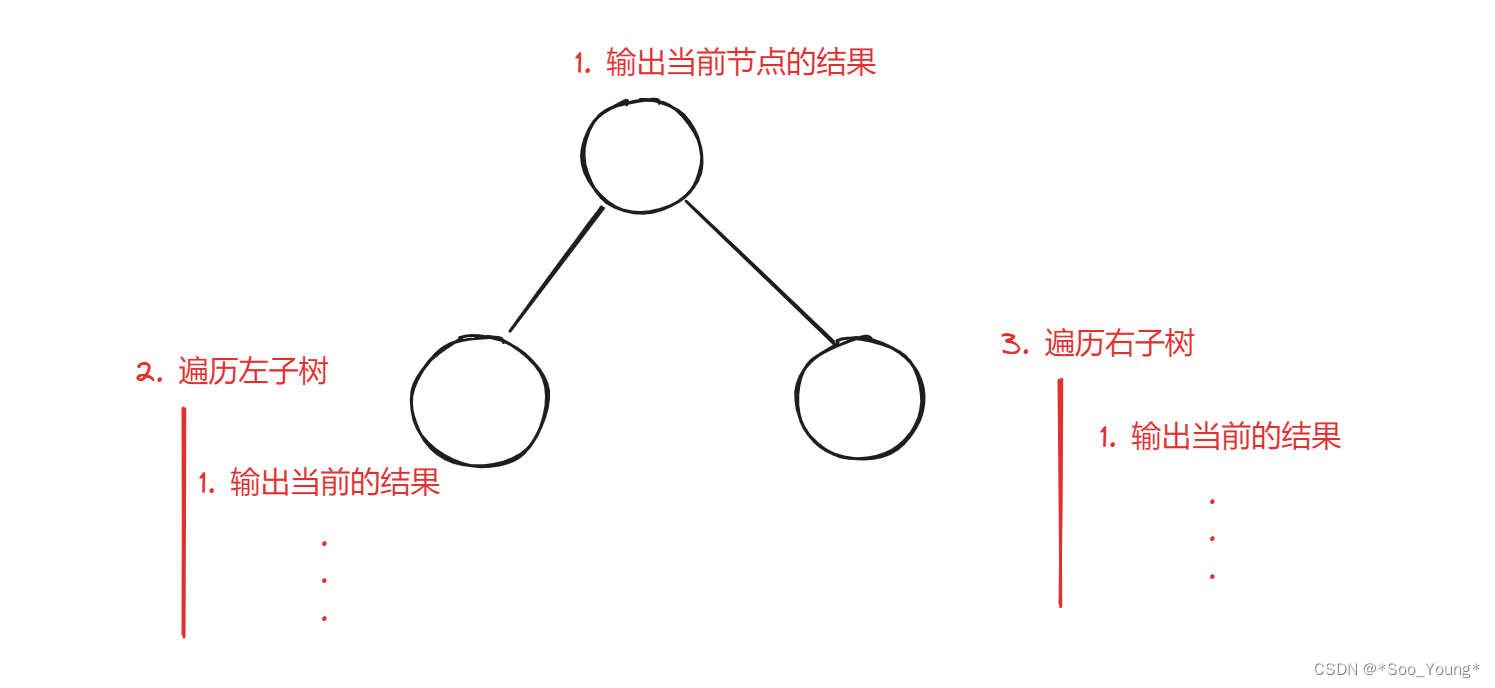
看我们上面的图是不是非常熟悉,这不就是前序遍历的遍历顺序吗?先中间再左边再右边,前序遍历无非就是对每个节点执行如上的相同的操作,那如何对每个节点操作呢?
递归的作用就是 帮助我们为每一个节点做相同的操作
我们只需要关注一个节点做的事情然后写到递归中,让递归帮我们去执行即可。
所有的递归都可以套用二叉树的模型来理解,我们知道,二叉树除了前序遍历,还有后序遍历和中序遍历:
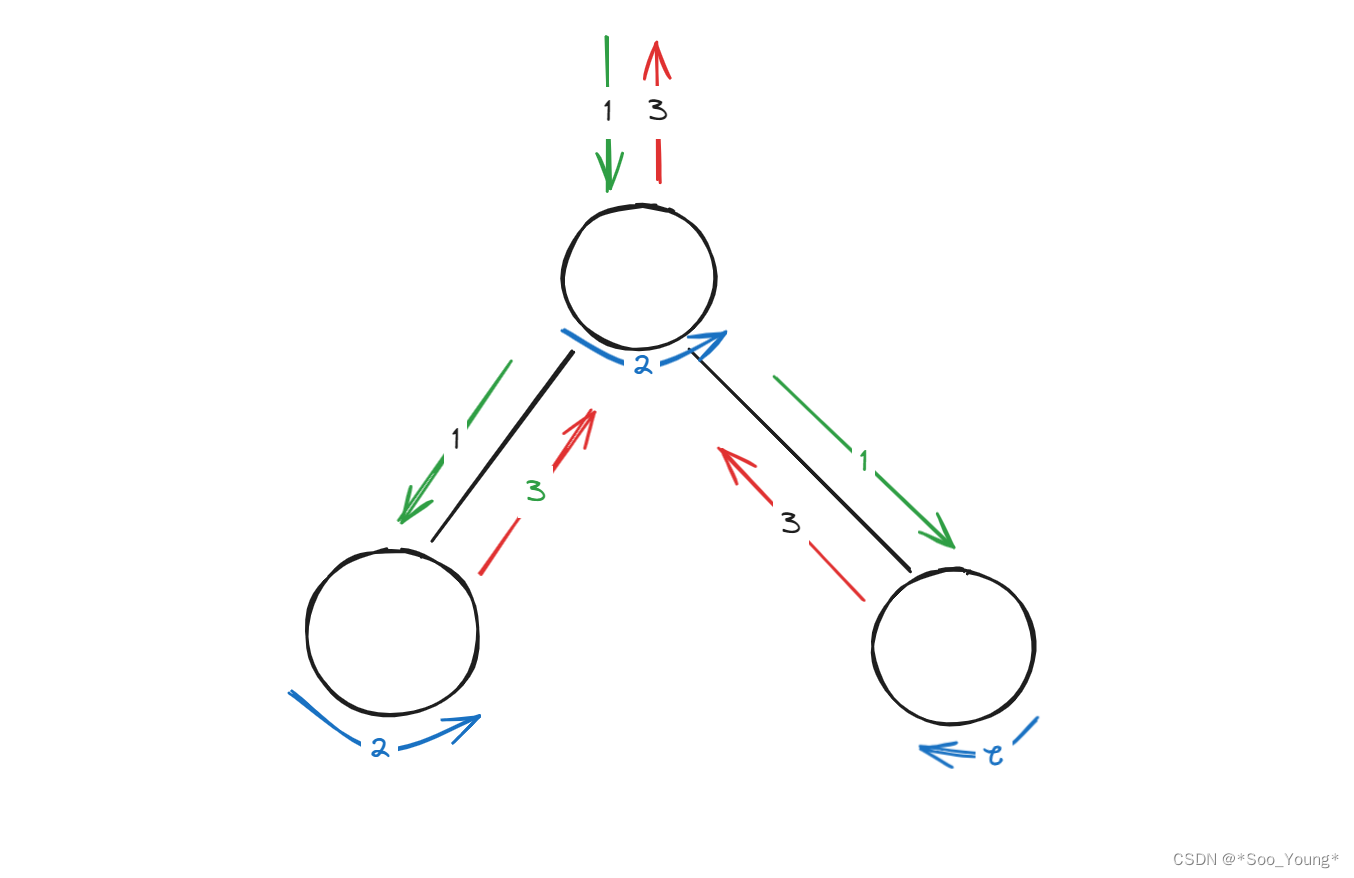
我们每次进入一个节点都可以分为三个位置:
- 前序位置
- 中序位置
- 后序位置
对应着上图中的 1 2 3 三个部分
前序中的操作即是我们进入这个节点后立马执行的操作,这不就是我们上面的前序遍历吗?进入节点后立马输出
中序就是在节点中执行的结果,即上图中的 2 ,这不就是左子树返回东西的地方吗?
那中序遍历的代码该怎么写?
public void reverse(TreeNode root) {if (root == null) {return;}reverse(root.left);res.add(root.val);reverse(root.right);}
}
到这里是不是对递归主键的清晰起来了?
后序遍历的代码我们也可以很轻松的写出来
public void reverse(TreeNode root) {if (root == null) {return;}reverse(root.left);res.add(root.val);reverse(root.right);}
}
如果上面的内容都能看懂,那么恭喜你已经解决了力扣上的三道题目:
No.144 二叉树的前序遍历
No.94 二叉树的中序遍历
No.145 二叉树的后序遍历
这里我们来看一个小小的问题:使用递归实现链表的倒序输出
如果将上面的部分看懂,那这道题相信对你来说很简单了
链表就是简化的二叉树,上面的每一个节点就可以通过上面的思路来处理
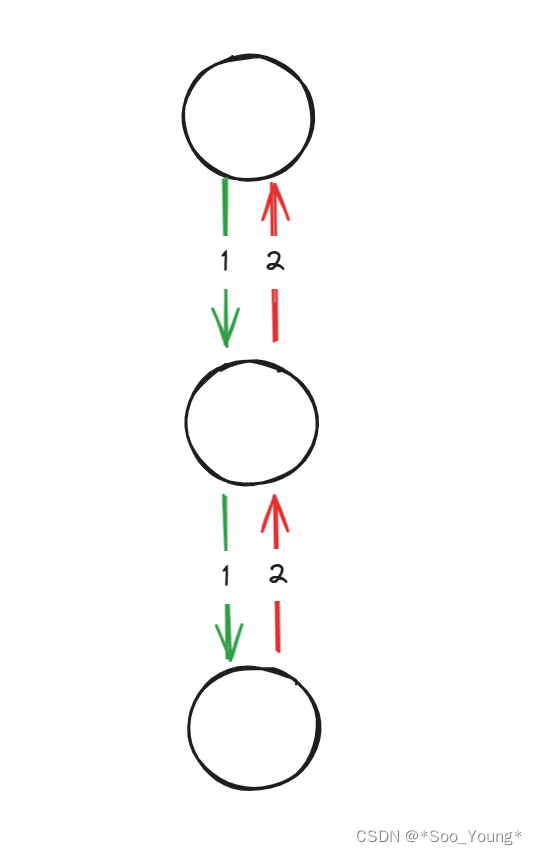
链表没有中序位置,只有前序和后序,既然要倒序输出链表,那我们要考虑的是我们的输出语句放在哪里
非常简单的二选一题目,肯定是放在后序的位置,呈现在代码中就是这样的:
public void reverse(ListNode head) {if (head == null) {return;}reverse(head.next);System.out.println(head.val);
}
03. 二叉树的非递归遍历
3.1 非递归实现前序遍历
二叉树的递归遍历上面已经提到过了,代码实现也非常容易,但如果让我们使用非递归的方式来模拟前序遍历就比较困难了。
递归的实现是通过栈来完成的,所以我们自然的去想使用栈来模拟前序遍历,之前刷关于栈的题目的时候总结过,一道题能否用栈去解决关键在于能否满足先进后出的特点。
前序遍历是对 每个节点 进行 中 左 右 顺序的遍历,我们要对每个节点都进行这种操作,就会出现将节点放入又取出来,就会有先进后出的特性。
比如我们来模拟一下对这个二叉树的遍历
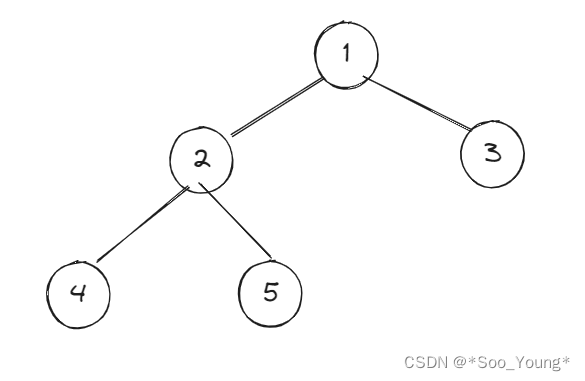
step 1
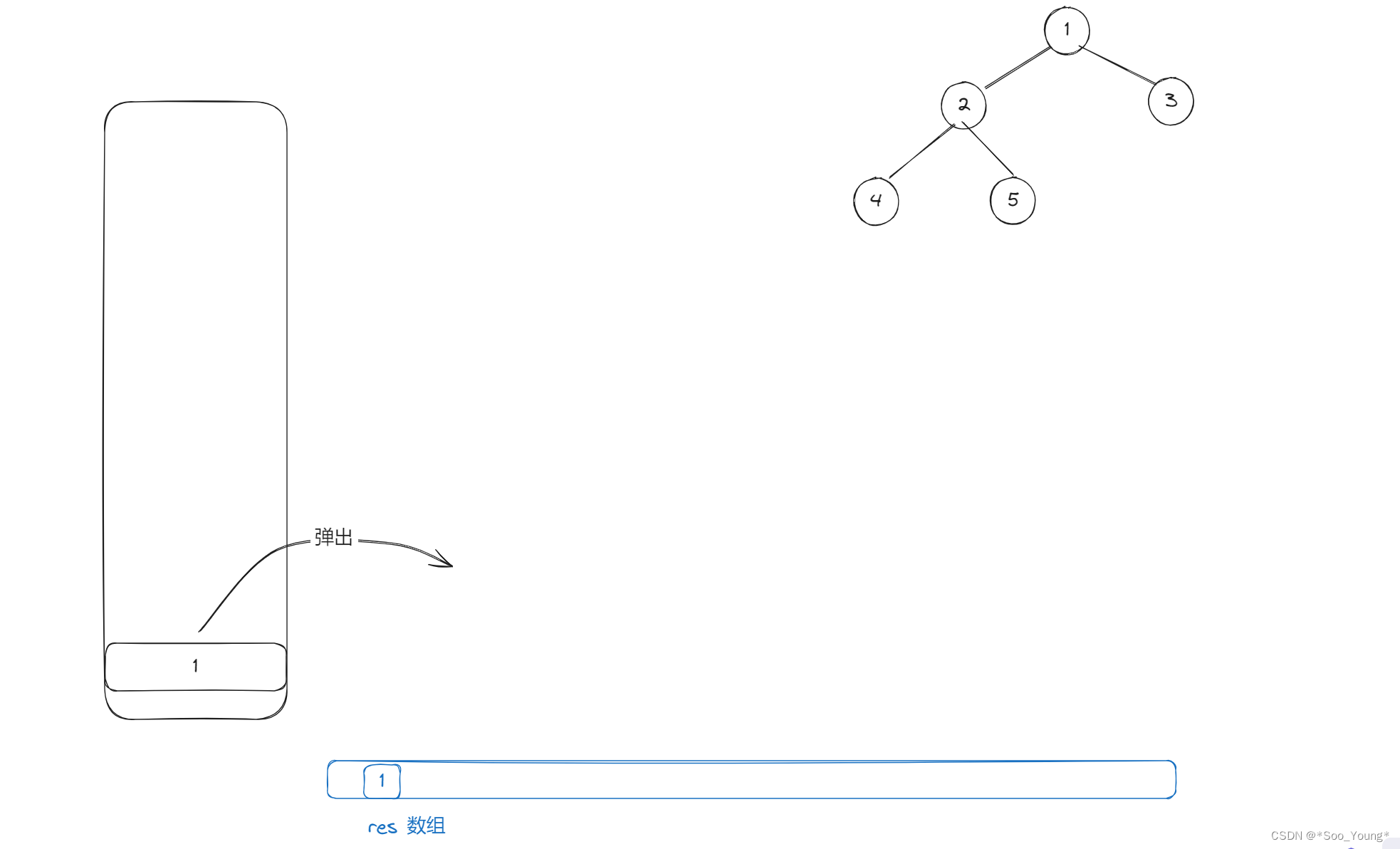
step2
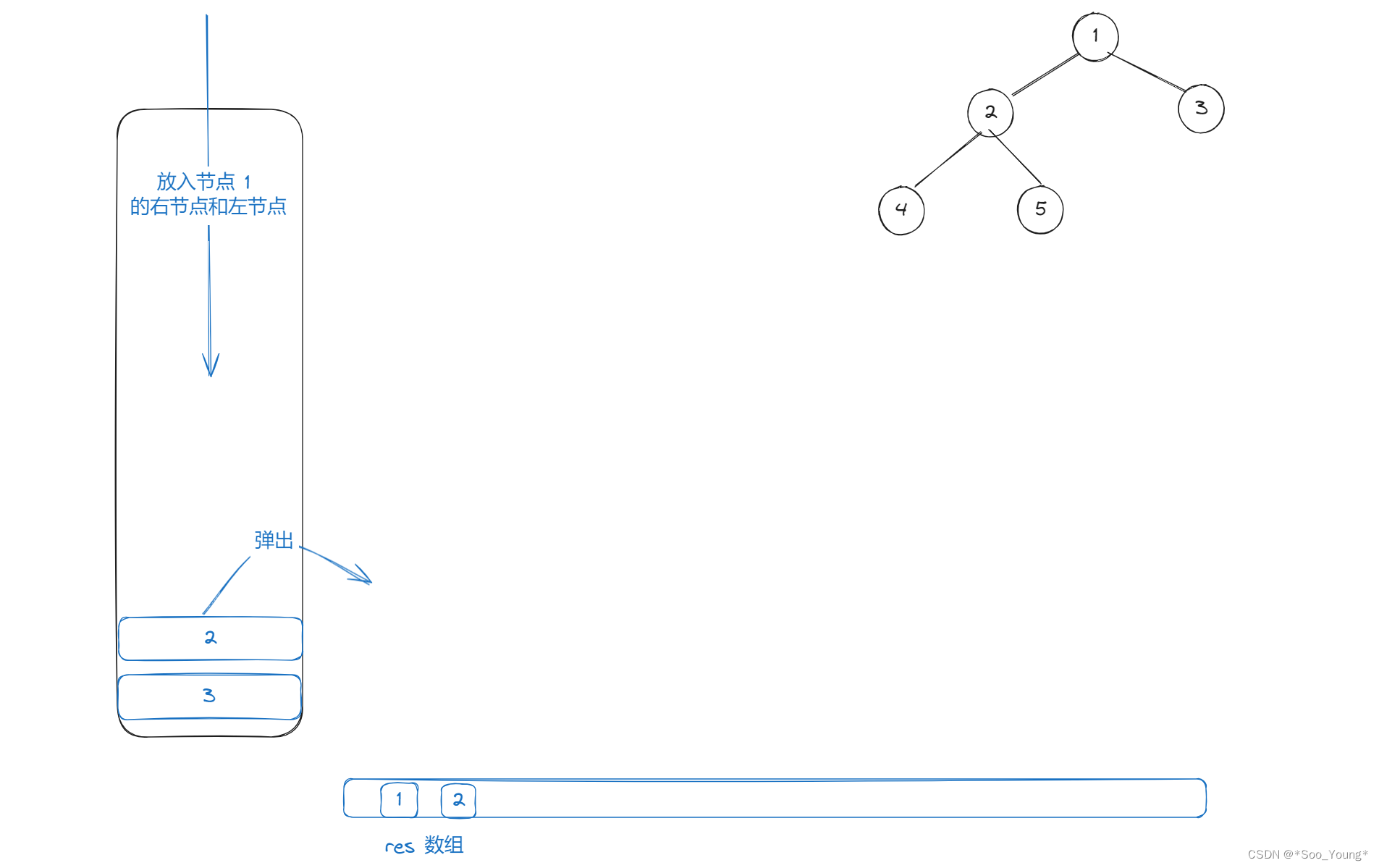
step3
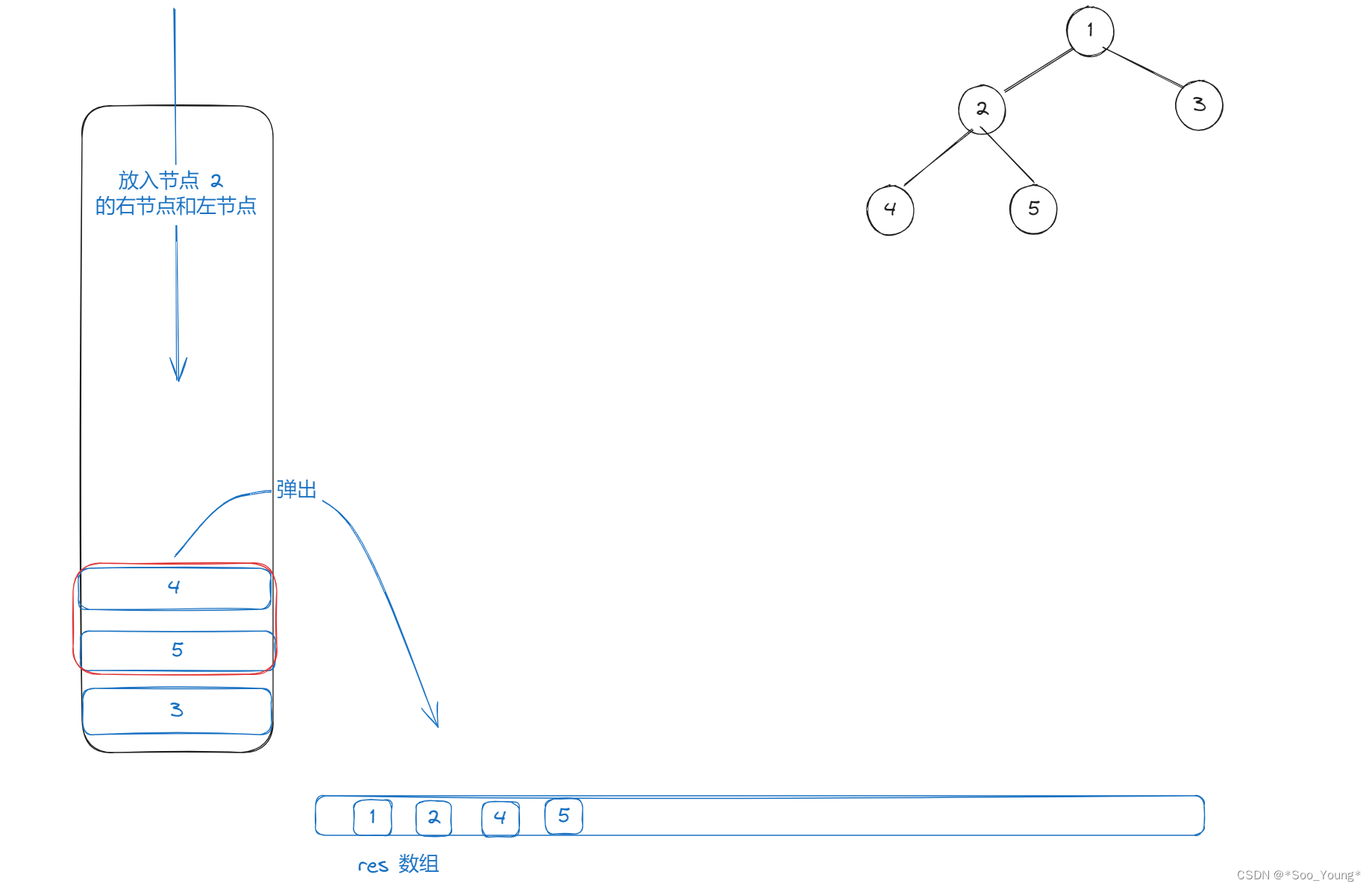
step4

和上面提到的一样,我们不用去模拟整个遍历的过程,我们只需要对每个节点进行的操作熟悉即可,再来总结一下上面的步骤:
- 将节点放入栈中
- 取出节点,存入结果数组
- 将节点的左节点放入栈中
- 将节点的右节点放入栈中
这样我们就用 非递归 的方式实现了前序遍历
这边给出代码,题目还是
No.144 二叉树的前序遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {Stack<TreeNode> stack = new Stack<>(); // 栈List<Integer> res = new ArrayList<>(); // 结果数组public List<Integer> preorderTraversal(TreeNode root) {stack.push(root);// 在 while 中持续执行上面提到的顺序while(!stack.isEmpty()) {TreeNode node = stack.pop();if (node != null) {res.add(node.val); stack.push(node.right);stack.push(node.left);}}return res;}
}
3.2 非递归实现二叉树的后序遍历
后序遍历的顺序是 左 右 中,而我们上面前序遍历的顺序是 中 左 右,如果我们入栈的时候先放入 左节点,也就是让右节点先弹出,遍历的顺序就变成了 中 右 左,这不就是后序遍历的逆序吗?
对入栈的元素进行上述处理后,再反转数组就可以实现后序遍历的效果
No.145 二叉树的后序遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {Stack<TreeNode> stack = new Stack<>(); // 栈List<Integer> res = new ArrayList<>(); // 结果数组public List<Integer> postorderTraversal(TreeNode root) {stack.push(root);// 在 while 中持续执行上面提到的顺序while(!stack.isEmpty()) {TreeNode node = stack.pop();if (node != null) {res.add(node.val); stack.push(node.left); // 先放入右节点stack.push(node.right);}}Collections.reverse(res);return res;}
}
3.3 非递归实现中序遍历
中序遍历的顺序是 右 中 左,但这不像上面的后序遍历可以通过调整顺序再倒置的方式解出。
对于这种遍历顺序和输出次序不同的方式,给出另一个思路,可以通过指针加栈的方式
因为中序遍历是深度优先遍历,我们输出的第一个元素是遍历到左边最底部再输出的,所以我们指定一个指针一直持续向左遍历,直到 current.left 指向 null 的时候,也就是所有的左节点全都遍历完,这就是我们要输出的第一个元素,此时将栈中的元素弹出放入数组中。
然后我们来单独看 current 此时指向这个节点,这是我们要 输出 的第一个节点,再次来回顾一下中序遍历的过程
- 进入节点一直向左遍历
- 左边没有元素的时候直接输出当前节点
- 向右边遍历,对右边的节点执行相同的操作
当我们将当前的节点放入结果数组的时候,就已经执行完了前两个步骤,接下来就是去遍历右节点,并且对右节点执行相同的操作。
这道题的重点仍然是将中心放在某一个节点上,因为我们用栈记录了遍历的节点,通过弹栈就可以实现对每个节点实现相同的操作,接下来只需要将思路翻译成代码即可。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {List<Integer> res = new ArrayList();TreeNode current;Stack<TreeNode> stack = new Stack<>();public List<Integer> inorderTraversal(TreeNode root) {if (root == null){return res;}current = root;while (current != null || !stack.isEmpty()) {if (current != null) {stack.push(current);current = current.left;} else {current = stack.pop();res.add(current.val); current = current.right; } }return res;}
}
04. 二叉树的广度优先搜索
层序遍历需要借助队列来实现,我们将每一层的元素一个个放到队列中,再逐一输出即可
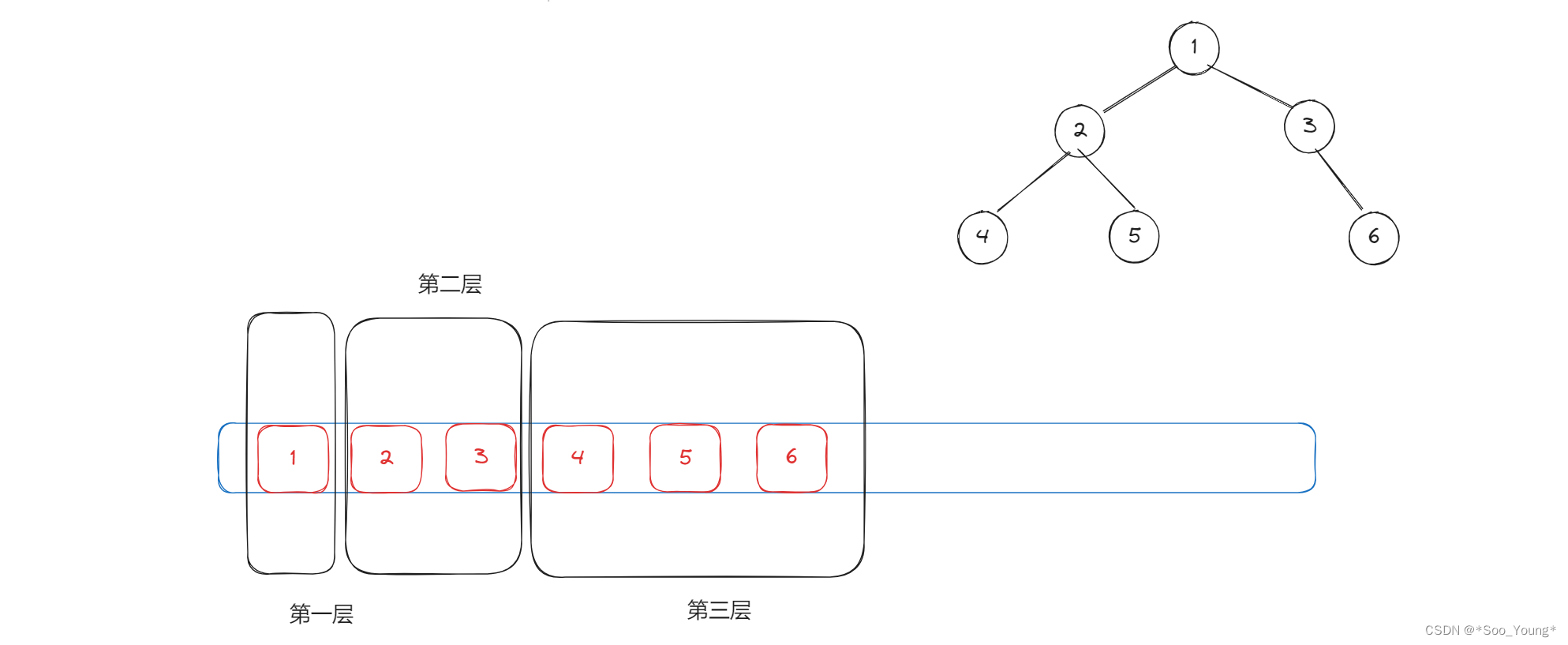
重要的就是要区分每一层有哪些元素,因为下一层元素的 add 是可以通过上一层元素弹出后再将其左右节点加入来实现的,所以我们需要一个变量 size 来记录每一层的元素个数。
利用 for 循环来输出每层的元素,此时 栈内剩下的元素 便是下一层的所有元素,此时更新我们的 size ,比如上图中的第二层中的元素遍历完后,栈内剩余的元素就是第三层的元素
No.102 二叉树的层序遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {Queue<TreeNode> queue = new LinkedList<>();List<List<Integer>> res = new ArrayList<>();public List<List<Integer>> levelOrder(TreeNode root) {if (root == null) {return res;}int size = 1; // 记录每层的元素个数queue.add(root);while (!queue.isEmpty()) {List<Integer> tempList = new ArrayList<>();// 对每一层进行遍历for (int i = size; i > 0; i--) {TreeNode tempNode = queue.poll();// 弹出队列中的元素if (tempNode != null) {tempList.add(tempNode.val);queue.add(tempNode.left);queue.add(tempNode.right);} }if (!tempList.isEmpty()){res.add(new ArrayList(tempList));}size = queue.size();// 更新 size 的长度}return res;}
}
1
相关文章:

代码随想录刷题笔记 DAY12 | 二叉树的理论基础 | 二叉树的三种递归遍历 | 二叉树的非递归遍历 | 二叉树的广度优先搜索
Day 12 01. 二叉树的理论基础 1.1 二叉树的种类 满二叉树:除了叶子节点以外,每个节点都有两个子节点,整个树是被完全填满的完全二叉树:除了底层以外,其他部分是满的,底部可以不是满的但是必须是从左到右连…...

Linux问题 apt-get install时 无法解析域名“cn.archive.ubuntu.com”
问题描述: 在安装程序时会出现无法解析域名的错误 解决办法: 1、编辑文件 sudo vim /etc/resolv.conf 2、在最后加上(按键 i 进入编辑模式) nameserver 8.8.8.8 3、保存退出(:wq)...

蓝桥--鸡哥的购物挑战OJ(4169)
题目: 思路: 暴力: 直接枚举所有得偶数区间,找最大值,n2超时 优化: 分类讨论,只要醉倒不重不漏得分类不出意外就能AC了 图中的选择方式很简单了,不做解释了。 AC代码(我的代码可…...

MySQL--删除数据表(6)
MySQL中删除数据表是非常容易操作的,但是你在进行删除表操作时要非常小心,因为执行删除命令后所有数据都会消失。 语法 以下为删除 MySQL 数据表的通用语法: DROP TABLE table_name ; -- 直接删除表,不检查是否存在 或 DROP…...
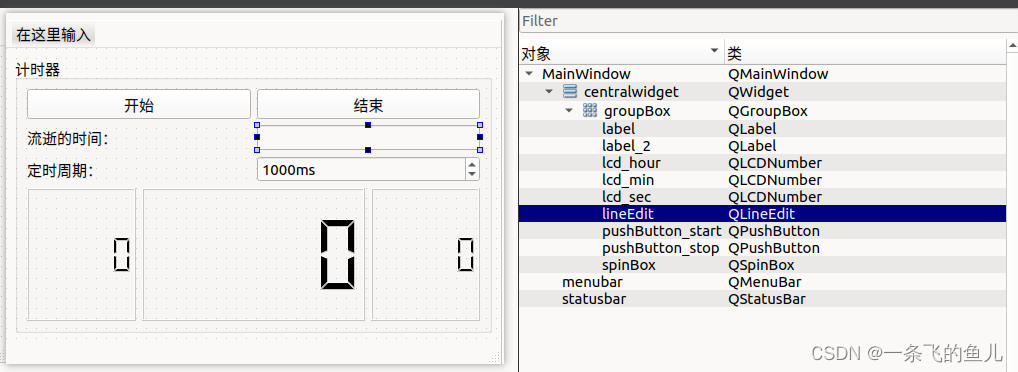
常用界面设计组件 —— 时间日期与定时器
2.7 时间日期与定时器2.7.1 时间日期相关的类2.7.2 日期时间数据与字符串之间的 转换2.7.3 QCalendarWidget日历组件2.7.4 定时器 2.7 时间日期与定时器 2.7.1 时间日期相关的类 时间日期是经常遇到的数据类型,Qt中时间日期类型的 类如下: QTime &…...
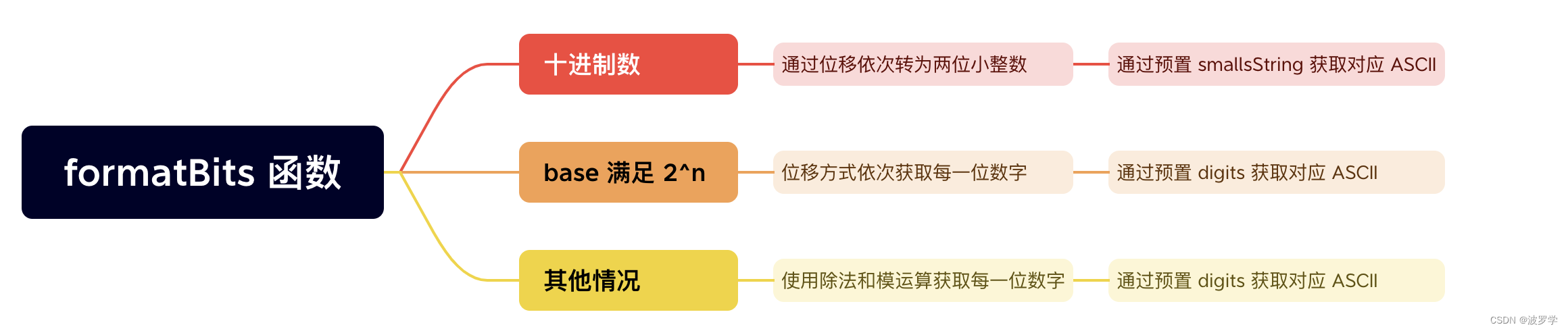
GO 中高效 int 转换 string 的方法与高性能源码剖析
文章目录 使用 strconv.Itoa使用 fmt.Sprintf使用 strconv.FormatIntFormatInt 深入剖析1. 快速路径处理小整数2. formatBits 函数的高效实现 结论 Go 语言 中,将整数(int)转换为字符串(string)是一项常见的操作。 本文…...
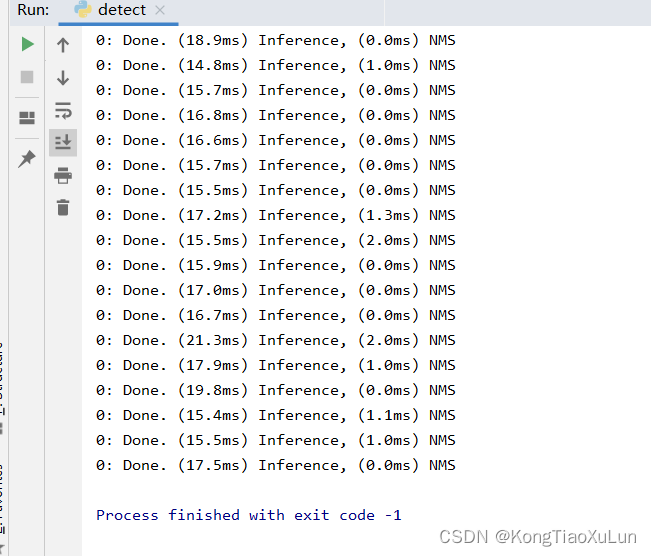
YOLOv7调用摄像头检测报错解决
yolov7detect.py文件调用本地摄像头,把source参数设为0 parser.add_argument(--source, typestr, default0, helpsource) # file/folder, 0 for webcam 报错:cv2.error: OpenCV(3.4.2) 一堆地址:The function is not implemented. Rebuild the library…...
Git学习 -- 分支合并、版本修改相关
目录 learn GIT Learn Git Branching merge和rebase的使用 基础命令 版本回退 工作区和暂存区 管理修改 撤销修改 删除修改 learn GIT Learn Git Branching 这是Gitee上的Git学习教程 Learn Git Branching Git Rebase Learn Git Branching 最终的实操 merge和rebase的…...
【小呆的力学笔记】弹塑性力学的初步认知二:应力应变分析(2)
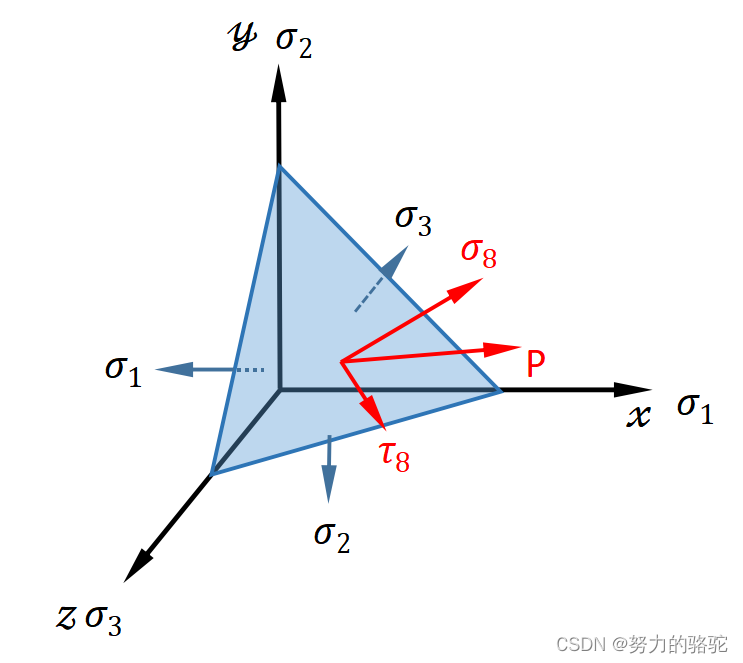
文章目录 1.4 主应力空间、八面体应力1.5 应变分析1.6 特殊应力、应变定义 1.4 主应力空间、八面体应力 一点的应力状态不论如何变化,其主应力和主方向一致的话,该点的应力状态就是唯一确定的。因此,我们用主应力方向建立一个三维坐标系来描…...
【学网攻】 第(6)节 -- 三层交换机实现VLAN间路由
文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻】 第(2)节 -- 交换机认识及使用【学网攻】 第(3)节 -- 交换机配置聚合端口【学网攻】 第(4)节 -- 交换机划分Vlan【学网攻】 第(5)节 -- Cisco VTP的使用 前言 网络已经成为了我们生活中不可或缺的一部分,它连接了…...

C++之内联函数
函数调用在执行时,首先要在栈中为形参和局部变量分配存储空间,然后还要将实参的值复制给形参,接下来还要将函数的返回地址(该地址指明了函数执行结束后,程序应该回到哪里继续执行)放入栈中,最后…...

【Bugku-web】alert
1.打开场景 2.按"CtrlU"查看源代码 3.翻到页面最末尾会有一个HTML实体编码,用在线工具在线Html实体编码解码后,得到flag值。...
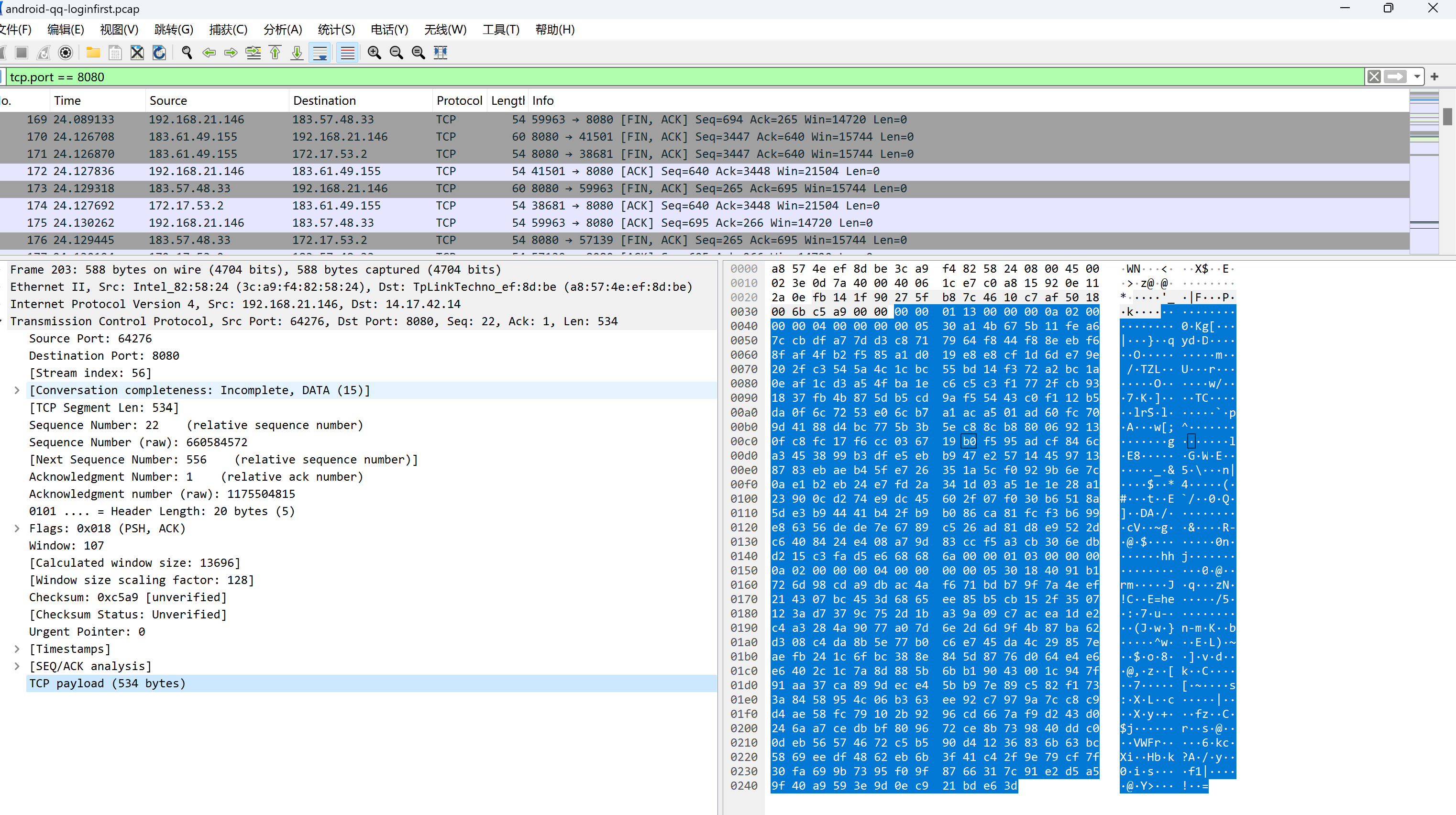
QQ数据包解密
Windows版qq数据包格式: android版qq数据包格式: 密钥:16个0 算法:tea_crypt算法 pc版qq 0825数据包解密源码: #include "qq.h" #include "qqcrypt.h" #include <WinSock2.h> #include…...

腾讯云上linux系统使用nginx,flask构建个人网站SSL证书过期换证书的操作步骤
ssl证书过期的时候,一般腾讯云提前一段时间给通知,让更换ssl证书,现在一般都可以免费更换,一般是一年期的,审核通过之后,需要下载nginx版本的证书,我的是4个文件,替换到nginx/cert文…...

git-clone的single-branch操作回退
(Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 最近使用git越来越多,一些git的功能使用也更熟悉了一些。 之前使用了single-branch下载分支,后来想取消掉,但怎么做呢,查了一些资料之后,了解到了怎么做&#x…...
03 SpringBoot实战 -微头条之首页门户模块(跳转某页面自动展示所有信息+根据hid查询文章全文并用乐观锁修改阅读量)
1.1 自动展示所有信息 需求描述: 进入新闻首页portal/findAllType, 自动返回所有栏目名称和id 接口描述 url地址:portal/findAllTypes 请求方式:get 请求参数:无 响应数据: 成功 {"code":"200","mes…...

YOCTO基础 - 创建meta层与bb文件
背景 在当前的嵌入式系统开发项目中,我们面临着构建定制化 Linux 发行版以满足项目需求的挑战。我们需要在目标硬件上运行一个轻量级、高度定制化的 Linux 映像,并确保它包含我们项目中所需的特定软件包和功能。为了实现这一目标,我们选择了…...

网络电视盒子哪个好?博主分享超高性价比网络电视盒子推荐
电视盒子是我们使用最多的数码产品,年货节很多朋友在纠结网络电视盒子哪个好,我这次的测评产品就是电视盒子,按照18款电视盒子的深度测评结果整理了网络电视盒子推荐,想知道网络电视盒子哪个好可以看看下面这五款电视盒子。 一&am…...

leetcode 刷题2
二分查找的绝妙运用: 看到有序数列,算法复杂度 0033. 搜索旋转排序数组 class Solution { public:int search(vector<int>& nums, int target) {int left 0;int right nums.size() - 1;while (left < right) {int mid left (right - …...
2-SAT问题相关理论和算法
前言 SAT 问题简介 SAT是可满足性、适定性(Satisfiability)问题的简称。一般形式为k-适定性问题或k-可满足性问题,简称 k-SAT。 何为布尔可满足性问题?给定一条真值表达式,包含逻辑变量、逻辑与、逻辑或以及非运算符,如&#x…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
