【小呆的力学笔记】弹塑性力学的初步认知二:应力应变分析(2)
文章目录
- 1.4 主应力空间、八面体应力
- 1.5 应变分析
- 1.6 特殊应力、应变定义
1.4 主应力空间、八面体应力
一点的应力状态不论如何变化,其主应力和主方向一致的话,该点的应力状态就是唯一确定的。因此,我们用主应力方向建立一个三维坐标系来描述问题将不失一般性,该坐标系如下图4,我们称之为主应力空间。我们考察等倾面组成的八面体,图中O’P点为等倾面ABC上面的应力向量 ( p 1 , p 2 , p 3 ) (p_1,p_2,p_3) (p1,p2,p3),八面体为等倾面八面体,即面ABC的法线方向余弦为 ( 1 3 , 1 3 , 1 3 ) (\frac{1}{\sqrt 3},\frac{1}{\sqrt 3},\frac{1}{\sqrt 3}) (31,31,31)。将O’P分解
O ’ P ‾ = O ’ Q ‾ + O ’ N ‾ (25) \overline {O’P}=\overline {O’Q}+\overline{O’N}\tag{25} O’P=O’Q+O’N(25)
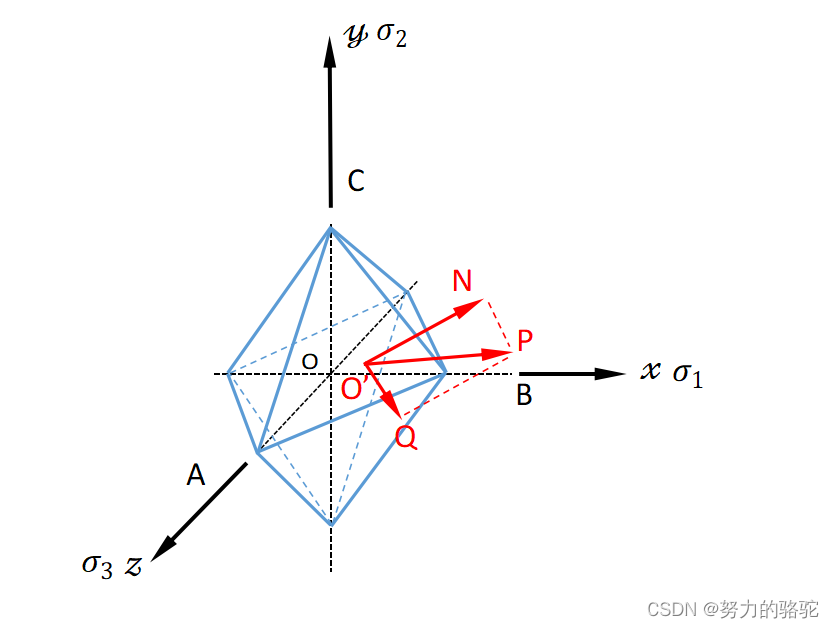
图 4 八面体 图4八面体 图4八面体
取等倾面和三个轴的坐标面组成的四面体为研究对象,如下图5所示。
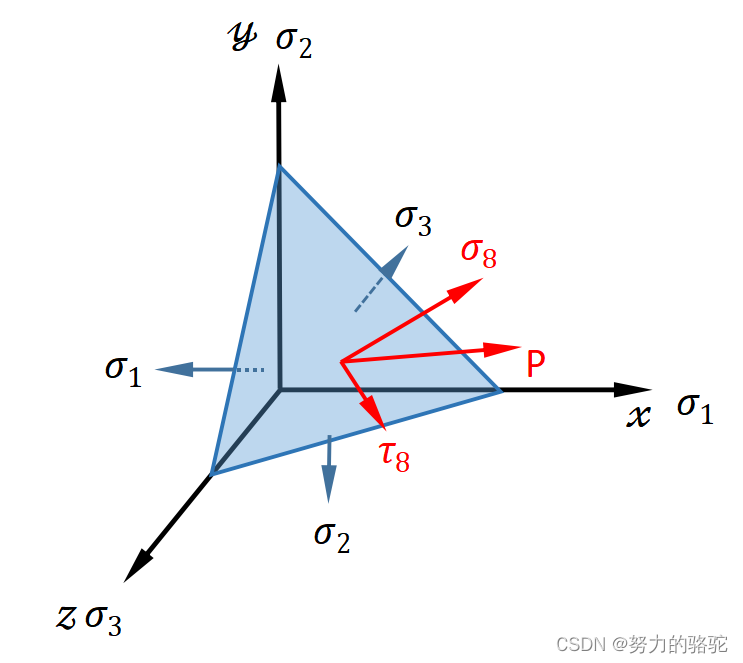
图 5 等倾面四面体 图5等倾面四面体 图5等倾面四面体
根据斜面应力公式 p j = σ i j n i p_j=\sigma_{ij}n_i pj=σijni,不难得到以下关系式(矩阵形式)
[ p 1 p 2 p 3 ] = [ σ 1 0 0 0 σ 2 0 0 0 σ 2 ] [ n 1 n 2 n 3 ] (26) \begin{bmatrix} p_1 \\ p_2\\p_3 \end{bmatrix}=\begin{bmatrix} \sigma_1 & 0 & 0\\ 0 & \sigma_2 & 0 \\0 & 0 & \sigma_2 \end{bmatrix}\begin{bmatrix} n_1 \\ n_2\\n_3 \end{bmatrix}\tag{26} p1p2p3 = σ1000σ2000σ2 n1n2n3 (26)
其中 ( n 1 , n 2 , n 3 ) = ( 1 3 , 1 3 , 1 3 ) (n_1 ,n_2,n_3)=(\frac{1}{\sqrt 3},\frac{1}{\sqrt 3},\frac{1}{\sqrt 3}) (n1,n2,n3)=(31,31,31)为等倾面的法线方向余弦。
那么,有
σ 8 = [ n 1 n 2 n 3 ] [ p 1 p 2 p 3 ] = σ 1 n 1 2 + σ 2 n 2 2 + σ 3 n 3 2 = 1 3 ( σ 1 + σ 2 + σ 3 ) = 1 3 I 1 (27) \sigma_8 = \begin{bmatrix} n_1 & n_2 & n_3 \end{bmatrix}\begin{bmatrix} p_1 \\ p_2\\p_3 \end{bmatrix}=\sigma_1n_1^2+\sigma_2n_2^2+\sigma_3n_3^2=\frac{1}{3}(\sigma_1+\sigma_2+\sigma_3)=\frac{1}{3}I_1 \tag{27} σ8=[n1n2n3] p1p2p3 =σ1n12+σ2n22+σ3n32=31(σ1+σ2+σ3)=31I1(27)
八面体相应的剪应力为
τ 8 = p 2 − σ 8 2 = p 1 2 + p 2 2 + p 3 2 − ( σ 1 n 1 2 + σ 2 n 2 2 + σ 3 n 3 2 ) 2 = σ 1 2 n 1 2 + σ 2 2 n 2 2 + σ 3 2 n 3 2 − ( σ 1 n 1 2 + σ 2 n 2 2 + σ 3 n 3 2 ) 2 = 1 3 ( σ 1 2 + σ 2 2 + σ 3 2 ) − 1 9 ( σ 1 + σ 2 + σ 3 ) 2 = 1 3 3 ( σ 1 2 + σ 2 2 + σ 3 2 ) − ( σ 1 2 + σ 2 2 + σ 3 2 + 2 σ 1 σ 2 + 2 σ 1 σ 3 + 2 σ 2 σ 3 ) = 1 3 ( σ 1 − σ 2 ) 2 + ( σ 1 − σ 3 ) 2 + ( σ 2 − σ 3 ) 2 = 2 3 J 2 = 1 3 s i j s i j (28) \tau_8 = \sqrt{p^2-\sigma_8^2}=\sqrt{p_1^2+p_2^2+p_3^2-(\sigma_1n_1^2+\sigma_2n_2^2+\sigma_3n_3^2)^2}\\ =\sqrt{\sigma_1^2n_1^2+\sigma_2^2n_2^2+\sigma_3^2n_3^2-(\sigma_1n_1^2+\sigma_2n_2^2+\sigma_3n_3^2)^2}\\ =\sqrt{\frac{1}{3}(\sigma_1^2+\sigma_2^2+\sigma_3^2)-\frac{1}{9}(\sigma_1+\sigma_2+\sigma_3)^2}\\ =\frac{1}{3}\sqrt{3(\sigma_1^2+\sigma_2^2+\sigma_3^2)-(\sigma_1^2+\sigma_2^2+\sigma_3^2+2\sigma_1\sigma_2+2\sigma_1\sigma_3+2\sigma_2\sigma_3)}\\ =\frac{1}{3}\sqrt{(\sigma_1-\sigma_2)^2+(\sigma_1-\sigma_3)^2+(\sigma_2-\sigma_3)^2}=\sqrt{\frac{2}{3}J_2}=\sqrt{\frac{1}{3}s_{ij}s_{ij}} \tag{28} τ8=p2−σ82=p12+p22+p32−(σ1n12+σ2n22+σ3n32)2=σ12n12+σ22n22+σ32n32−(σ1n12+σ2n22+σ3n32)2=31(σ12+σ22+σ32)−91(σ1+σ2+σ3)2=313(σ12+σ22+σ32)−(σ12+σ22+σ32+2σ1σ2+2σ1σ3+2σ2σ3)=31(σ1−σ2)2+(σ1−σ3)2+(σ2−σ3)2=32J2=31sijsij(28)
1.5 应变分析
应变分析的内容同应力分析内容,只是注意一点,应变张量和工程应变在剪应变分量是不同的,定义如下。
[ ε x x ε y x ε z x ε x y ε y y ε z y ε x z ε y z ε z z ] = [ ε x x 1 2 γ y x 1 2 γ z x 1 2 γ x y ε y y 1 2 γ z y 1 2 γ x z 1 2 γ y z ε z z ] (29) \begin{bmatrix} \varepsilon_{xx} & \varepsilon_{yx} & \varepsilon_{zx}\\ \varepsilon_{xy} & \varepsilon_{yy} & \varepsilon_{zy}\\ \varepsilon_{xz} & \varepsilon_{yz} & \varepsilon_{zz} \end{bmatrix}= \begin{bmatrix} \varepsilon_{xx} & \frac{1}{2}\gamma_{yx} & \frac{1}{2}\gamma_{zx}\\ \frac{1}{2}\gamma_{xy} & \varepsilon_{yy} & \frac{1}{2}\gamma_{zy}\\ \frac{1}{2}\gamma_{xz} & \frac{1}{2}\gamma_{yz} & \varepsilon_{zz} \end{bmatrix}\tag{29} εxxεxyεxzεyxεyyεyzεzxεzyεzz = εxx21γxy21γxz21γyxεyy21γyz21γzx21γzyεzz (29)
同样定义应变偏张量,有如下形式
[ e x x e y x e z x e x y e y y e z y e x z e y z e z z ] = [ ε x x ε y x ε z x ε x y ε y y ε z y ε x z ε y z ε z z ] − [ ε m 0 0 0 ε m 0 0 0 ε m ] (30) \begin{bmatrix} e_{xx} & e_{yx} & e_{zx}\\ e_{xy} & e_{yy} & e_{zy}\\ e_{xz} & e_{yz} & e_{zz} \end{bmatrix}= \begin{bmatrix} \varepsilon_{xx} & \varepsilon_{yx} & \varepsilon_{zx}\\ \varepsilon_{xy} & \varepsilon_{yy} & \varepsilon_{zy}\\ \varepsilon_{xz} & \varepsilon_{yz} & \varepsilon_{zz} \end{bmatrix}-\begin{bmatrix} \varepsilon_{m} & 0 & 0\\ 0 & \varepsilon_{m} & 0\\ 0 & 0 & \varepsilon_{m} \end{bmatrix}\tag{30} exxexyexzeyxeyyeyzezxezyezz = εxxεxyεxzεyxεyyεyzεzxεzyεzz − εm000εm000εm (30)
其中 ε m = 1 3 ( ε x x + ε y y + ε z z ) \varepsilon_{m}=\frac{1}{3}(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}) εm=31(εxx+εyy+εzz)
1.6 特殊应力、应变定义
定义应力强度或等效应力 σ ‾ \overline\sigma σ为
σ ‾ = 3 J 2 = 3 2 s i j s i j = 1 2 [ ( σ 1 − σ 2 ) 2 + ( σ 1 − σ 3 ) 2 + ( σ 2 − σ 3 ) 2 ] = 1 2 [ ( σ x x − σ y y ) 2 + ( σ x x − σ z z ) 2 + ( σ y y − σ z z ) 2 + 6 ( τ x z 2 + τ x y 2 + τ y z 2 ) ] (31) \overline\sigma=\sqrt{3J_2}=\sqrt{\frac{3}{2}s_{ij}s_{ij}}\\ =\sqrt{\frac{1}{2}[(\sigma_{1}-\sigma_{2})^2+(\sigma_{1}-\sigma_{3})^2+(\sigma_{2}-\sigma_{3})^2]}\\ =\sqrt{\frac{1}{2}[(\sigma_{xx}-\sigma_{yy})^2+(\sigma_{xx}-\sigma_{zz})^2+(\sigma_{yy}-\sigma_{zz})^2+6(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)]} \tag{31} σ=3J2=23sijsij=21[(σ1−σ2)2+(σ1−σ3)2+(σ2−σ3)2]=21[(σxx−σyy)2+(σxx−σzz)2+(σyy−σzz)2+6(τxz2+τxy2+τyz2)](31)
定义应变强度或等效应变 ε ‾ \overline \varepsilon ε为
ε ‾ = 2 3 e i j e i j (32) \overline \varepsilon=\sqrt{\frac{2}{3}e_{ij}e_{ij}} \tag{32} ε=32eijeij(32)
定义剪切等效应力 T ‾ \overline T T为
T ‾ = 1 2 s i j s i j (33) \overline T=\sqrt{\frac{1}{2}s_{ij}s_{ij}} \tag{33} T=21sijsij(33)
定义剪切等效应变 Γ ‾ \overline\Gamma Γ为
Γ ‾ = 2 e i j e i j (34) \overline\Gamma=\sqrt{2e_{ij}e_{ij}} \tag{34} Γ=2eijeij(34)
加上上面定义的八面体剪应力、八面体剪应变
τ 8 = 1 3 s i j s i j γ 8 = 4 3 e i j e i j (35) \tau_8=\sqrt{\frac{1}{3}s_{ij}s_{ij}}\\ \gamma_8=\sqrt{\frac{4}{3}e_{ij}e_{ij}}\tag{35} τ8=31sijsijγ8=34eijeij(35)
至于为什么定义这些应力应变,我们在后面再介绍。
相关文章:

【小呆的力学笔记】弹塑性力学的初步认知二:应力应变分析(2)
文章目录 1.4 主应力空间、八面体应力1.5 应变分析1.6 特殊应力、应变定义 1.4 主应力空间、八面体应力 一点的应力状态不论如何变化,其主应力和主方向一致的话,该点的应力状态就是唯一确定的。因此,我们用主应力方向建立一个三维坐标系来描…...
【学网攻】 第(6)节 -- 三层交换机实现VLAN间路由
文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻】 第(2)节 -- 交换机认识及使用【学网攻】 第(3)节 -- 交换机配置聚合端口【学网攻】 第(4)节 -- 交换机划分Vlan【学网攻】 第(5)节 -- Cisco VTP的使用 前言 网络已经成为了我们生活中不可或缺的一部分,它连接了…...

C++之内联函数
函数调用在执行时,首先要在栈中为形参和局部变量分配存储空间,然后还要将实参的值复制给形参,接下来还要将函数的返回地址(该地址指明了函数执行结束后,程序应该回到哪里继续执行)放入栈中,最后…...

【Bugku-web】alert
1.打开场景 2.按"CtrlU"查看源代码 3.翻到页面最末尾会有一个HTML实体编码,用在线工具在线Html实体编码解码后,得到flag值。...
QQ数据包解密
Windows版qq数据包格式: android版qq数据包格式: 密钥:16个0 算法:tea_crypt算法 pc版qq 0825数据包解密源码: #include "qq.h" #include "qqcrypt.h" #include <WinSock2.h> #include…...

腾讯云上linux系统使用nginx,flask构建个人网站SSL证书过期换证书的操作步骤
ssl证书过期的时候,一般腾讯云提前一段时间给通知,让更换ssl证书,现在一般都可以免费更换,一般是一年期的,审核通过之后,需要下载nginx版本的证书,我的是4个文件,替换到nginx/cert文…...

git-clone的single-branch操作回退
(Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 最近使用git越来越多,一些git的功能使用也更熟悉了一些。 之前使用了single-branch下载分支,后来想取消掉,但怎么做呢,查了一些资料之后,了解到了怎么做&#x…...
03 SpringBoot实战 -微头条之首页门户模块(跳转某页面自动展示所有信息+根据hid查询文章全文并用乐观锁修改阅读量)
1.1 自动展示所有信息 需求描述: 进入新闻首页portal/findAllType, 自动返回所有栏目名称和id 接口描述 url地址:portal/findAllTypes 请求方式:get 请求参数:无 响应数据: 成功 {"code":"200","mes…...

YOCTO基础 - 创建meta层与bb文件
背景 在当前的嵌入式系统开发项目中,我们面临着构建定制化 Linux 发行版以满足项目需求的挑战。我们需要在目标硬件上运行一个轻量级、高度定制化的 Linux 映像,并确保它包含我们项目中所需的特定软件包和功能。为了实现这一目标,我们选择了…...

网络电视盒子哪个好?博主分享超高性价比网络电视盒子推荐
电视盒子是我们使用最多的数码产品,年货节很多朋友在纠结网络电视盒子哪个好,我这次的测评产品就是电视盒子,按照18款电视盒子的深度测评结果整理了网络电视盒子推荐,想知道网络电视盒子哪个好可以看看下面这五款电视盒子。 一&am…...

leetcode 刷题2
二分查找的绝妙运用: 看到有序数列,算法复杂度 0033. 搜索旋转排序数组 class Solution { public:int search(vector<int>& nums, int target) {int left 0;int right nums.size() - 1;while (left < right) {int mid left (right - …...
2-SAT问题相关理论和算法
前言 SAT 问题简介 SAT是可满足性、适定性(Satisfiability)问题的简称。一般形式为k-适定性问题或k-可满足性问题,简称 k-SAT。 何为布尔可满足性问题?给定一条真值表达式,包含逻辑变量、逻辑与、逻辑或以及非运算符,如&#x…...
【大数据精讲】全量同步与CDC增量同步方案对比
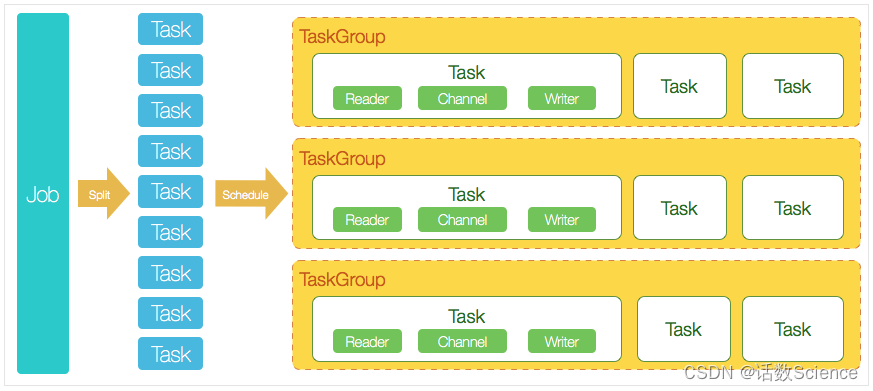
目录 背景 名词解释 问题与挑战 FlinkCDC DataX 工作原理 调度流程 五、DataX 3.0六大核心优势 性能优化 背景 名词解释 CDC CDC又称变更数据捕获(Change Data Capture),开启cdc的源表在插入INSERT、更新UPDATE和删除DELETE活动时…...

自定义通用返回对象
目的:给返回对象补充一些信息,告诉前端这个请求在业务层面上是成功还是失败,以及具体的描述信息。 我们需要自定义错误码(因为前端的HTTP状态码默认的值比较少)和正常错误返回类。 ErrorCode : package …...

从0开始python学习-51.pytest之接口加密封装
目录 MD5加密 base64加密 rsa加密 MD5加密 1. 封装加密方法 def md5_encode(self,data):data str(data).encode("utf-8")md5_data hashlib.md5(data).hexdigest()return md5_data 2. 写入需要使用加密的接口yaml用例 -request:method: posturl: http://192.168.…...

c++的命名空间
命名空间 一.c的关键字二.命名空间2.1 命名空间定义2.1 命名空间的使用2.1.1加命名空间名称及作用域限定符2.1.2使用using将命名空间中某个成员引入 三.标准命名空间std 一.c的关键字 c中一共有63个关键字 关键字11111asmdoifreturntrycontinueautodoubleinlineshorttypedeff…...
)
阿富汗塔利班兴起时的比赛代码3475:练85.3 删数问题(Noip1994)
【题目描述】 输入一个高精度的正整数n�,去掉其中任意s�个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的n�和s�,寻找一种方案使得剩下的数字组成的新数最小。 输出新的正整数。࿰…...

大数据平台红蓝对抗 - 磨利刃,淬精兵!
背景 目前大促备战常见备战工作:专项压测(全链路压测、内部压测)、灾备演练、降级演练、限流、巡检(监控、应用健康度)、混沌演练(红蓝对抗),如下图所示。随着平台业务越来越复杂&a…...
【2024-01-22】某极验3流程分析-滑块验证码
声明:该专栏涉及的所有案例均为学习使用,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!如有侵权,请私信联系本人删帖! 文章目录 一、前言二、抓包流程分析1.刷新页面2.点击按钮进行验证…...

Laya2.13.3接入FGUI
下载与复制文件与Laya1.x类似,可以看我上一篇: Laya1.8.4接入FariyGui,以及其中踩的坑-CSDN博客 不同的是: 两个库文件需要在index.js中引入 新建一个脚本将fgui中搭建好的UI包引入: export default class GameApp…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
