阿富汗塔利班兴起时的比赛代码3475:练85.3 删数问题(Noip1994)
【题目描述】
输入一个高精度的正整数n�,去掉其中任意s�个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的n�和s�,寻找一种方案使得剩下的数字组成的新数最小。
输出新的正整数。(n�不超过240240位)
输入数据均不需判错。
【输入】
共两行,第一行为n�;第二行s�。
【输出】
最后剩下的最小数。
【输入样例】
175438
4
【输出样例】
13
#include<bits/stdc++.h>
using namespace std;
int x;
string s;
int main()
{ cin>>s>>x;while(x--){int i;for(i=0;i<s.size();i++){if(s[i]>s[i+1]){s.erase(s.begin()+i);break;}}}int i=0;while(s[i]=='0'){i++;}while(i<s.size()){cout<<s[i];i++;}return 0;
}相关文章:
)
阿富汗塔利班兴起时的比赛代码3475:练85.3 删数问题(Noip1994)
【题目描述】 输入一个高精度的正整数n�,去掉其中任意s�个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的n�和s�,寻找一种方案使得剩下的数字组成的新数最小。 输出新的正整数。࿰…...

大数据平台红蓝对抗 - 磨利刃,淬精兵!
背景 目前大促备战常见备战工作:专项压测(全链路压测、内部压测)、灾备演练、降级演练、限流、巡检(监控、应用健康度)、混沌演练(红蓝对抗),如下图所示。随着平台业务越来越复杂&a…...
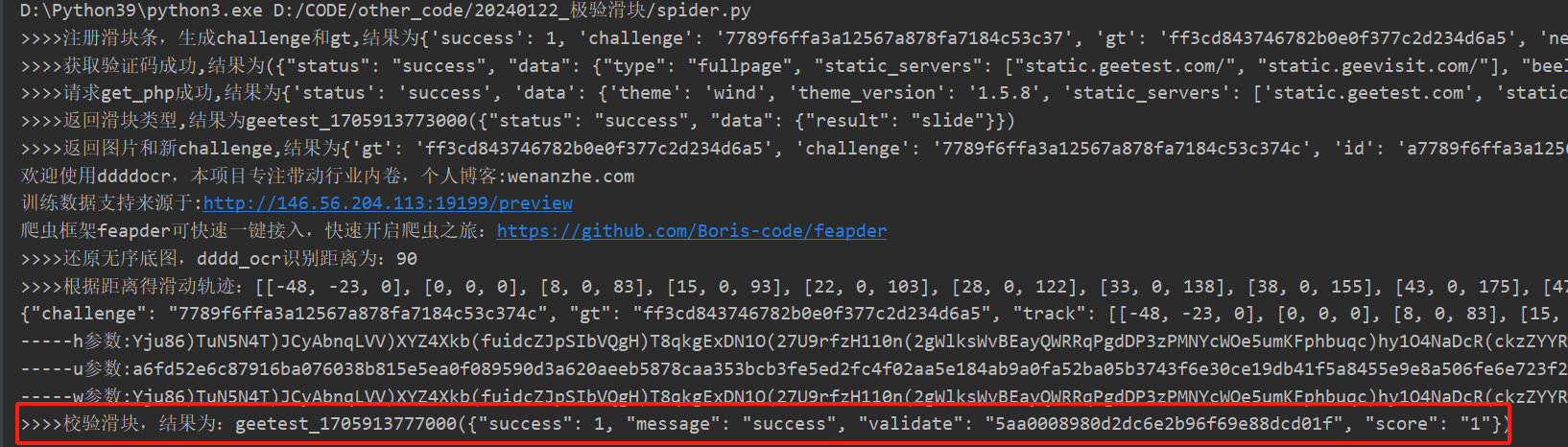
【2024-01-22】某极验3流程分析-滑块验证码
声明:该专栏涉及的所有案例均为学习使用,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!如有侵权,请私信联系本人删帖! 文章目录 一、前言二、抓包流程分析1.刷新页面2.点击按钮进行验证…...

Laya2.13.3接入FGUI
下载与复制文件与Laya1.x类似,可以看我上一篇: Laya1.8.4接入FariyGui,以及其中踩的坑-CSDN博客 不同的是: 两个库文件需要在index.js中引入 新建一个脚本将fgui中搭建好的UI包引入: export default class GameApp…...
短视频账号矩阵系统+无人直播系统源码技术开发
短视频账号矩阵系统无人直播系统源码技术开发涉及到多个领域,包括但不限于前端开发、后端开发、数据库设计、网络通信等。 以下是一些基本技术的步骤和注意事项: 1.技术需求分析设计:首先,需要明确开发短视频账号矩阵系统和无人直…...
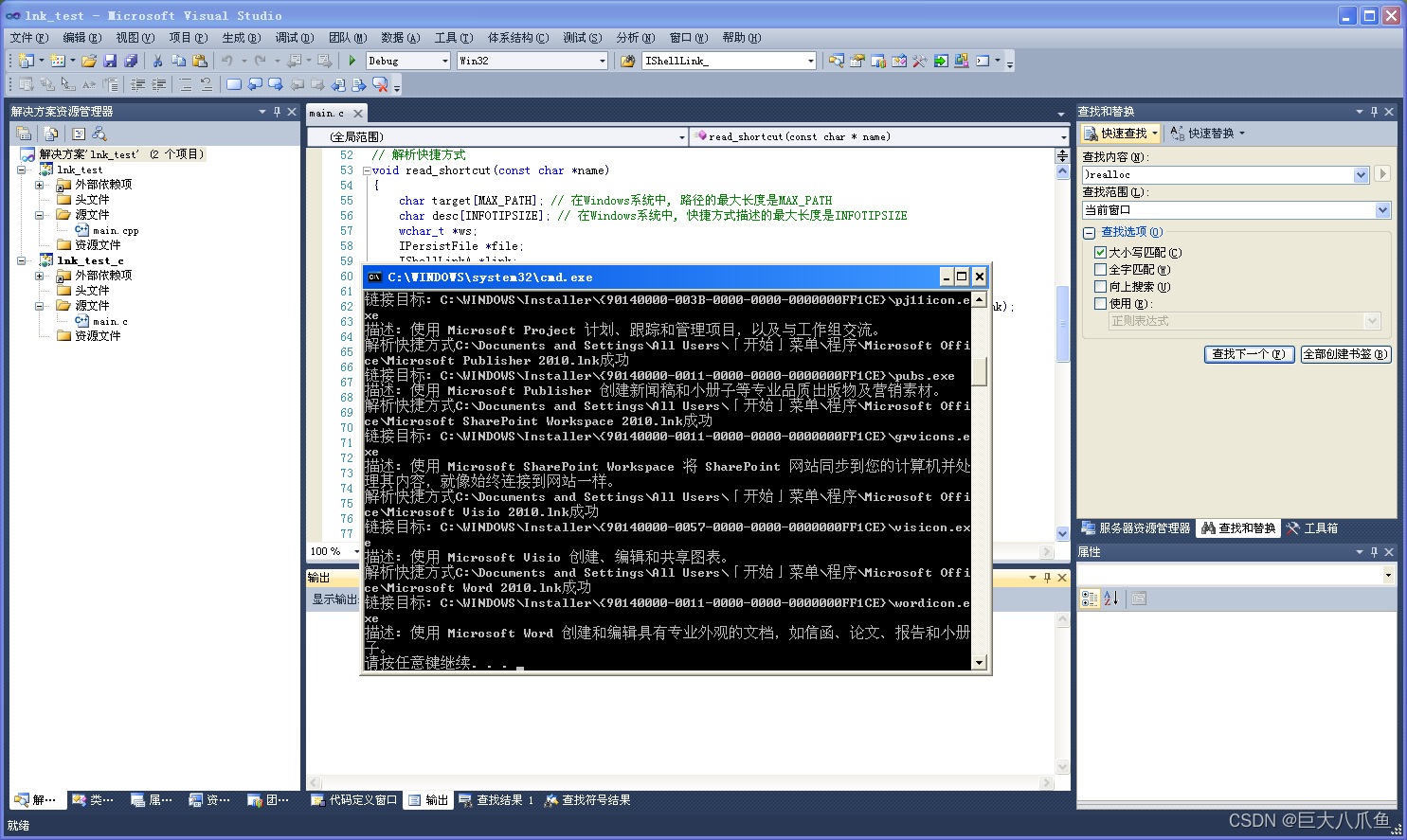
C语言或C++通过IShellLinkA创建或解析lnk快捷方式(使用char字符数组)
本例程用到的COM接口有IShellLinkA和IPersistFile。 请注意因为函数参数的类型不为BSTR,所以这两个接口可直接传char *或wchar_t *字符串,不需要提前转化为BSTR类型。 C语言的写法: /* 这个程序只能在C编译器下编译成功, 请确保源文件的扩展…...

Spring源码学习-Spring流程概述(一)
Spring启动的流程 public class Test {public static void main(String[] args) {ClassPathXmlApplicationContext context new ClassPathXmlApplicationContext("applicationContext.xml");Student bean context.getBean(Student.class);context.close();} }调用…...
Figma怎么设置中文,Figma有中文版吗?
不是很多人不想用 Figma,真是因为纯英文界面而头疼。这就是为什么有人会到处搜索 Figma 如何设置中文这样的问题。 然后我们直接快刀斩乱麻,Figma 没有中文版,但是我们还有其他的方法:例如, Figma 添加一个插件来解决…...
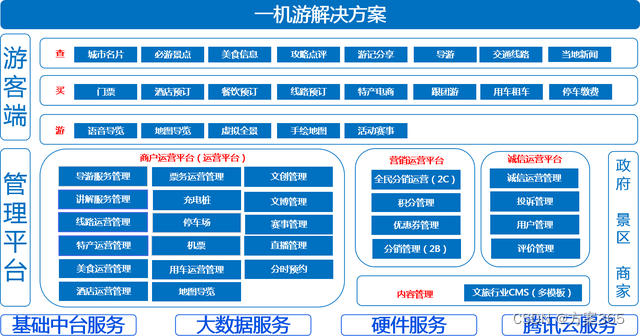
智慧文旅一机游:科技与文化的完美结合,引领智慧文旅新潮流,智慧旅游未来已来
一、科技与文化的完美结合:智慧文旅一机游的核心理念 智慧文旅一机游,是科技与文化相融合的产物,它不仅代表着旅游行业的创新与发展,更是一种文化与科技完美结合的生活方式。一机游的核心理念在于通过先进的科技手段,提…...

多维时序 | Matlab实现CNN-LSTM-Mutilhead-Attention卷积长短期记忆神经网络融合多头注意力机制多变量时间序列预测
多维时序 | Matlab实现CNN-LSTM-Mutilhead-Attention卷积长短期记忆神经网络融合多头注意力机制多变量时间序列预测 目录 多维时序 | Matlab实现CNN-LSTM-Mutilhead-Attention卷积长短期记忆神经网络融合多头注意力机制多变量时间序列预测效果一览基本介绍程序设计参考资料 效果…...
软件工程实验报告(完整)
博主介绍:✌全网粉丝喜爱、前后端领域优质创作者、本质互联网精神、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战✌有需要可以联系作者我哦! 🍅附上相关C语言版源码讲解🍅 ὄ…...

Java零基础学习20:集合的练习
编写博客目的:本系列博客均根据B站黑马程序员系列视频学习和编写目的在于记录自己的学习点滴,方便后续回忆和查找相关知识点,不足之处恳请各位有缘的朋友指正。 一、查找id对应的集合索引 package www.itheima;import java.util.ArrayList;…...
【latex】在Overleaf的IEEE会议模板中,快速插入参考文献
【LaTeX】在Overleaf的IEEE会议模板中,快速插入参考文献 写在最前面第一步:在文献检索网站导出引用文献的bib文件第二步:编辑overleaf模版方法二:EduBirdie生成参考文献(补充)使用LaTeX在Overleaf的IEEE会议…...
)
java反射之Field用法(获取对象的字段名和属性值)
一、概述 Field是一个类,位于java.lang.reflect包下。在Java反射中Field类描述的是类的属性信息,功能包括: 获取当前对象的成员变量的类型 对成员变量重新设值 二、如何获取Field类对象 getField(String name): 获取类特定的方法,…...

Java Web(三)--CSS
介绍 为什么需要: 在没有 CSS 之前,想要修改 HTML 元素的样式需要为每个 HTML 元素单独定义样式属性,费心费力;CSS 可以让 html 元素(内容) 样式(CSS)分离,提高web 开发的工作效率(针对前端开发),从而…...

天津大数据培训班推荐,数据分析过程的常见错误
大数据”是近年来IT行业的热词,目前已经广泛应用在各个行业。大数据,又称海量信息,特点是数据量大、种类多、实时性强、数据蕴藏的价值大。大数据是对大量、动态、能持续的数据,通过运用分析、挖掘和整理,实现数据信息…...

【笔记】Helm-3 主题-17 弃用的Kubernetes API
弃用的Kubernetes API Kubernetes是一个API驱动系统,且API会随着时间的推移而变化,以反映对问题理解的不断推移。这是系统及API的普遍做法。API推移的一个重要部分是良好的弃用策略和通知用户更改API是如何实现的。换句话说,您的API使用者需要…...

麒麟系统—— openKylin 安装 java
麒麟系统—— openKylin 安装 java JDK 一、准备工作1. 确保麒麟系统 openKylin 已经安装完毕。2. 了解 java JDK 的版本信息,以便下载合适的安装包。 二、安装 java JDK3. 将下载好的 java JDK 安装包解压到指定目录。4. 配置环境5. 验证安装结果 本文将分享如何在…...

HTML学习笔记——07:其他嵌入技术
除了将图像、视频和音频嵌入到网页上,还能让你在网页中嵌入各种内容类型的元素:<iframe>, <embed> 和 <object> 元素。 <iframe>用于嵌入其他网页,另外两个元素则允许你嵌入 PDF,SVG,甚至 Fl…...
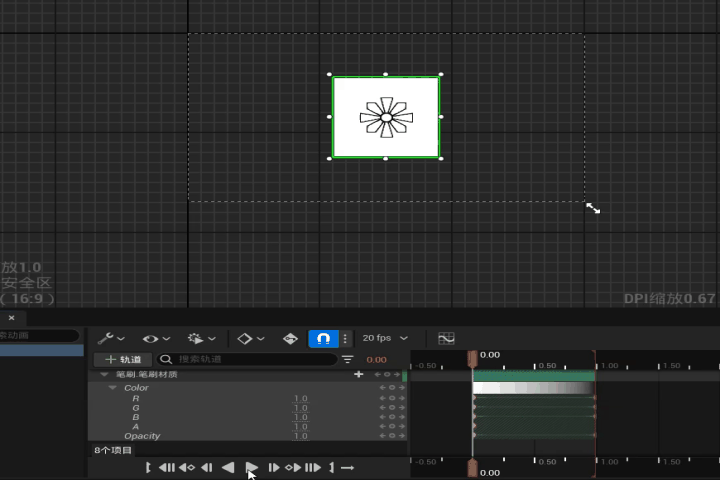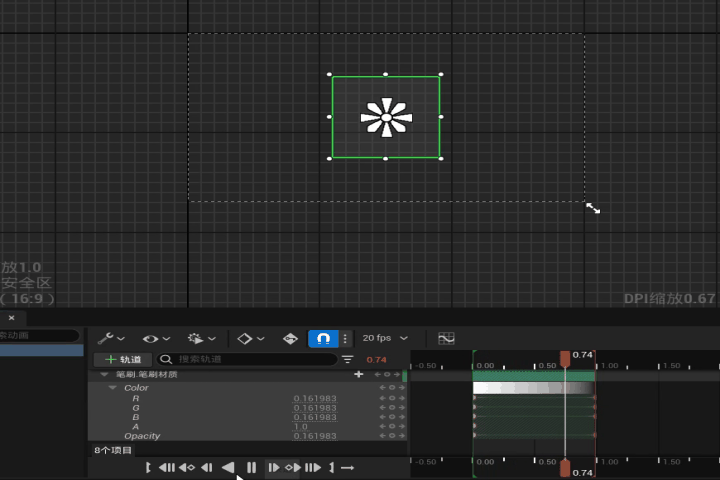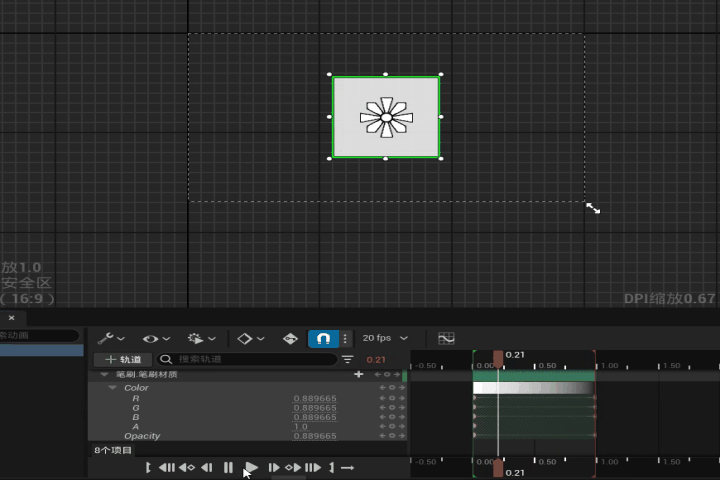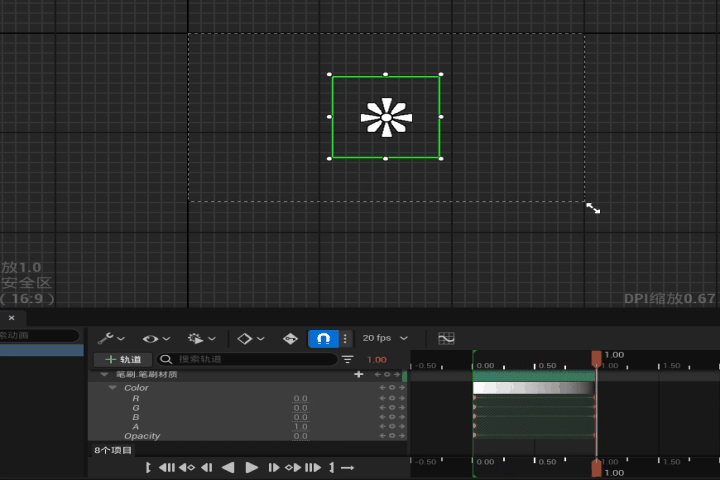
【UE】在控件蓝图中通过时间轴控制材质参数变化
效果 步骤 1. 新建一个控件蓝图和一个材质 2. 打开材质,设置材质域为用户界面,混合模式设置为“半透明” 在材质图表中添加两个参数来控制材质的颜色和不透明度 3. 对材质创建材质实例 4. 打开控件蓝图,在画布面板中添加一个图像控件 将刚…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
