【算法设计-枚举、分治】素数、约数、质因数分解
文章目录
- 1. 素数判定
- 2. 素数筛选法
- 3. 质因数分解
- 4. 求一个数的约数
- 5. 求两个数的最大公约数(GCD)
- 6. 求两个数的最小公倍数(LCM)
1. 素数判定
判定从 2 到sqrt(n)依次能否把 n 整除,若存在可以整除的数则说明 n 不是素数,若都不可以整除则说明 n 是素数。
注意:2 是特殊的素数。
为什么到sqrt(n)就可以了呢?请观察下面两个合数的例子:
30 分解为两个因数相乘:
- 2 x 15
- 3 x 10
- 5 x 6
- 6 x 5
- 10 x 3
- 15 x 2
36 分解为两个因数相乘:
- 2 x 18
- 3 x 12
- 4 x 9
- 6 x 6
- 9 x 4
- 12 x 3
- 18 x 2
发现当越过sqrt(n)后,得到的两个因数与sqrt(n)前相同(只是位置对调了而已),因此没有必要对sqrt(n)后的数进行试除。
#include <cstdio>
#include <cmath>
using namespace std;bool isPrime (int x){if (x == 2)return true;else{int bound = sqrt(x);for (int i = 2; i <= bound; i++)if (x % i == 0) return false;}return true;
}int main(){int n;while (scanf("%d", &n) != EOF){bool flag = isPrime(n);if (flag)printf("Yes\n");elseprintf("No\n");}return 0;
}
2. 素数筛选法
原理:
- 2 是素数,把 2 后面所有能被 2 整除的数都划去;
- 2 后面第一个没划去的数是 3,把 3 留下,3 后面所有能被 3 整除的数都划去;
- 3 后面第一个没划去的数是 5,把 5 留下,5 后面所有能被 5 整除的数都划去;
- 5 后面第一个没划去的数是 7,把 7 留下,7 后面所有能被 7 整除的数都划去;
- …
注意:每次划去当前质数的倍数时,可能存在某些数被重复筛选的情况,如 8 既被 2 又被 4 筛选。在枚举筛选的时候可以进行剪枝,当 i 为素数时,注意到i * k (k < i)必定已经在求得 k 的某个素数因子时被标记过,因此可以从i * i开始。
#include <math.h>
#include <stdio.h>
#include <string.h>#define MAX 10000bool isPrime[MAX+1];int main(){int n;scanf("%d", &n);memset(isPrime, true, sizeof(isPrime)); // memset函数包含于string.h头文件中 for (int i = 2; i <= sqrt(n); i++){if (isPrime[i]){ // 发现是素数,下面将素数的倍数都标记为非素数for (int j = i * i; j < n; j += i) // i*k(k<i)必定已经在求得k的某个素数因子时被标记过,因此从i*i开始 isPrime[j] = false;}}for (int i = 2; i < n; i++)if (isPrime[i]) printf("%d ", i);return 0;
}
3. 质因数分解
输入:
994
输出:
2 7 71
代码:
#include <math.h>
#include <stdio.h>
#include <string.h>#define MAX 10000bool isPrime[MAX+1];int main(){int n;scanf("%d", &n);memset(isPrime, true, sizeof(isPrime)); // memset函数包含于string.h头文件中 int bound = sqrt(n);// 标记素数 for (int i = 2; i <= bound; i++){if (isPrime[i]){ // 发现是素数,下面将素数的倍数都标记为非素数for (int j = i * i; j < n; j += i) // i*k(k<i)必定已经在求得k的某个素数因子时被标记过,因此从i*i开始 isPrime[j] = false;}}// 分解质因数for (int i = 2; i <= bound; i++){if (isPrime[i]){ // 如果是质数,则开始试除 while (n % i == 0){ // 若发现能整除,则继续使用这个质数除下去 n = n / i;printf("%d ", i);}}} if (n > 1) // 若除完后,结果不是1,说明剩下来的是质数 printf("%d", n);return 0;
}
4. 求一个数的约数
在自然数(0和正整数)的范围内,
4的正约数有:1、2、4。
6的正约数有:1、2、3、6。
10的正约数有:1、2、5、10。
12的正约数有:1、2、3、4、6、12。
15的正约数有:1、3、5、15。
18的正约数有:1、2、3、6、9、18。
20的正约数有:1、2、4、5、10、20。
注意:一个数的约数必然包括1及其本身。
#include <cstdio>
#include <cmath>
using namespace std;int main(){int n;while (scanf("%d", &n) != EOF){for (int i = 1; i <= sqrt(n); i++){if (n % i == 0){printf("%d %d ", i, n / i);}}printf("\n");}return 0;
}
5. 求两个数的最大公约数(GCD)
辗转相除法:两个整数的最大公约数等于其中较小的数和两数相除的余数的最大公约数,即gcd(a,b) = gcd(b, a mod b)。
基本思想:分治。
原理:若整数 g 为 a、b 的最大公约数,则有:
a = g x l(1)
b = g x m(2)
a、b 又可以表示为:
a = b x k + r(即a / b = k···r)(3)
把(1)(2)代入到(3):
g x l = g x m x k + r,即r = g x (l - m x k)
注意到r = a mod b,因此a mod b = g x (l - m x k)(4)
联合(2)(4),这样问题变为了求 b 和 a mod b 的最大公约数:
b = g x m(2)
a mod b = g x (l - m x k)(5)
递归写法:
// 辗转相除法求最大公约数(12和18的最大公约数:6)
int gcd (int a, int b){if (b == 0)return a;elsereturn gcd(b, a % b);
}
非递归写法:
// 辗转相除法求最大公约数(12和18的最大公约数:6)
int gcd (int a, int b){while (b != 0){int rem = a % b;a = b;b = rem;}return a;
}
6. 求两个数的最小公倍数(LCM)
// 求最小公倍数(12和18的最小公倍数:36)
int lcm (int a, int b){return a * b / gcd(a, b);
}
相关文章:

【算法设计-枚举、分治】素数、约数、质因数分解
文章目录1. 素数判定2. 素数筛选法3. 质因数分解4. 求一个数的约数5. 求两个数的最大公约数(GCD)6. 求两个数的最小公倍数(LCM)1. 素数判定 判定从 2 到sqrt(n)依次能否把 n 整除,若存在可以整除的数则说明 n 不是素数…...
)
【第十四届蓝桥杯】第三期模拟赛B组C++题解(待修正+持续更新-ing)
文章目录写在前面一、找最小数题目描述解题报告1、大体思路2、代码详解二、求列名题目描述解题报告1、大体思路2、代码详解三、求日期数题目描述解题报告1、大体思路2、代码详解四、取数题目描述解题报告1、大体思路2、代码详解五、最大连通分块题目描述解题报告1、大体思路2、…...
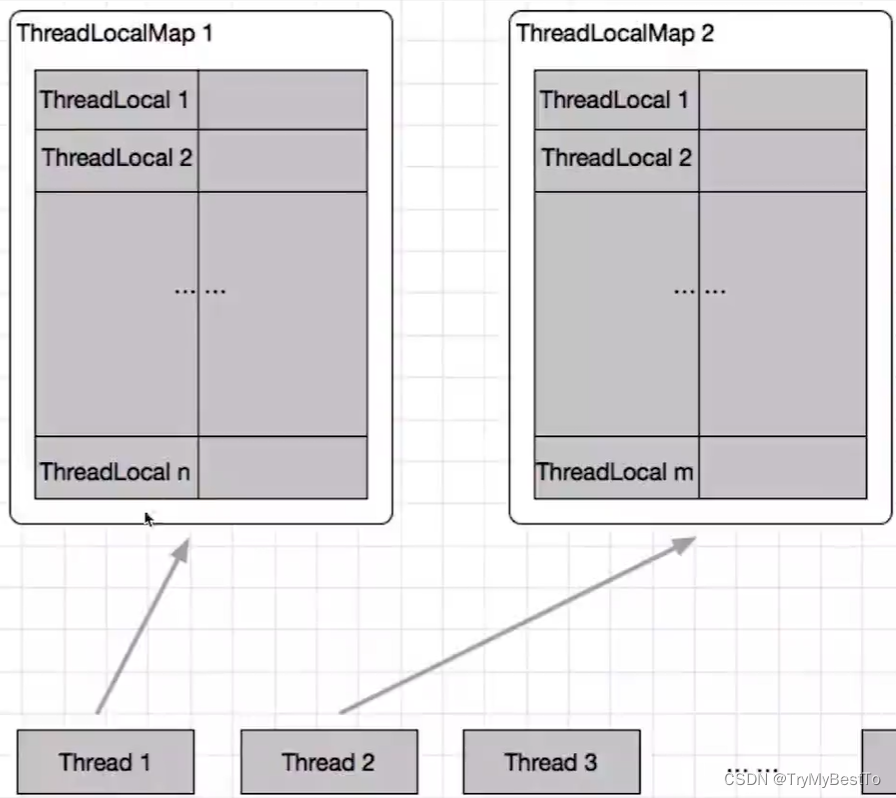
线程池和ThreadLocal详解
线程池和ThreadLocal详解线程池池化模式:线程池里的线程数量设定为多少比较合适?添加线程规则:实现原理:线程池实现任务复用的原理线程池状态:Executors 创线程池工具类手动创建(更推荐):自动创…...
)
[深入理解SSD系列综述 1.7] SSD固态存储市场发展分析与预测_固态存储技术发展方向(2022to2023)
前言 自2020年疫情爆发以来,远程办公、网上教育、流媒体等等应用引爆对消费电子及云服务的需求增长,全球数字化转型加速,带来了两年的闪存风光时刻。然而,进入2022年,在俄乌冲突、疫情重燃、通胀上升等一系列事件冲击下,全球经济下行风险加剧,对智能手机、PC等科技产品的…...
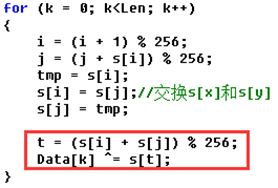
【2021.12.25】ctf逆向中常见加密算法和编码识别
【2021.12.25】ctf逆向中常见加密算法和编码识别(含exe及wp) 文章目录【2021.12.25】ctf逆向中常见加密算法和编码识别(含exe及wp)0、前言1、基础加密手法2、base64(1)原理:(2&#…...

【数据结构初阶】堆排序
目录 前言 概念 堆排序的实现 1.建堆 (1)堆向上调整算法 (2)堆的向下调整算法 2. 利用堆删除思想来进行排序 3.堆排序的时间复杂度 4.源码 总结 前言 前边我们学习了堆的实现,对堆的每个接口都进行了详细的讲…...

Day5: platformDriver-1
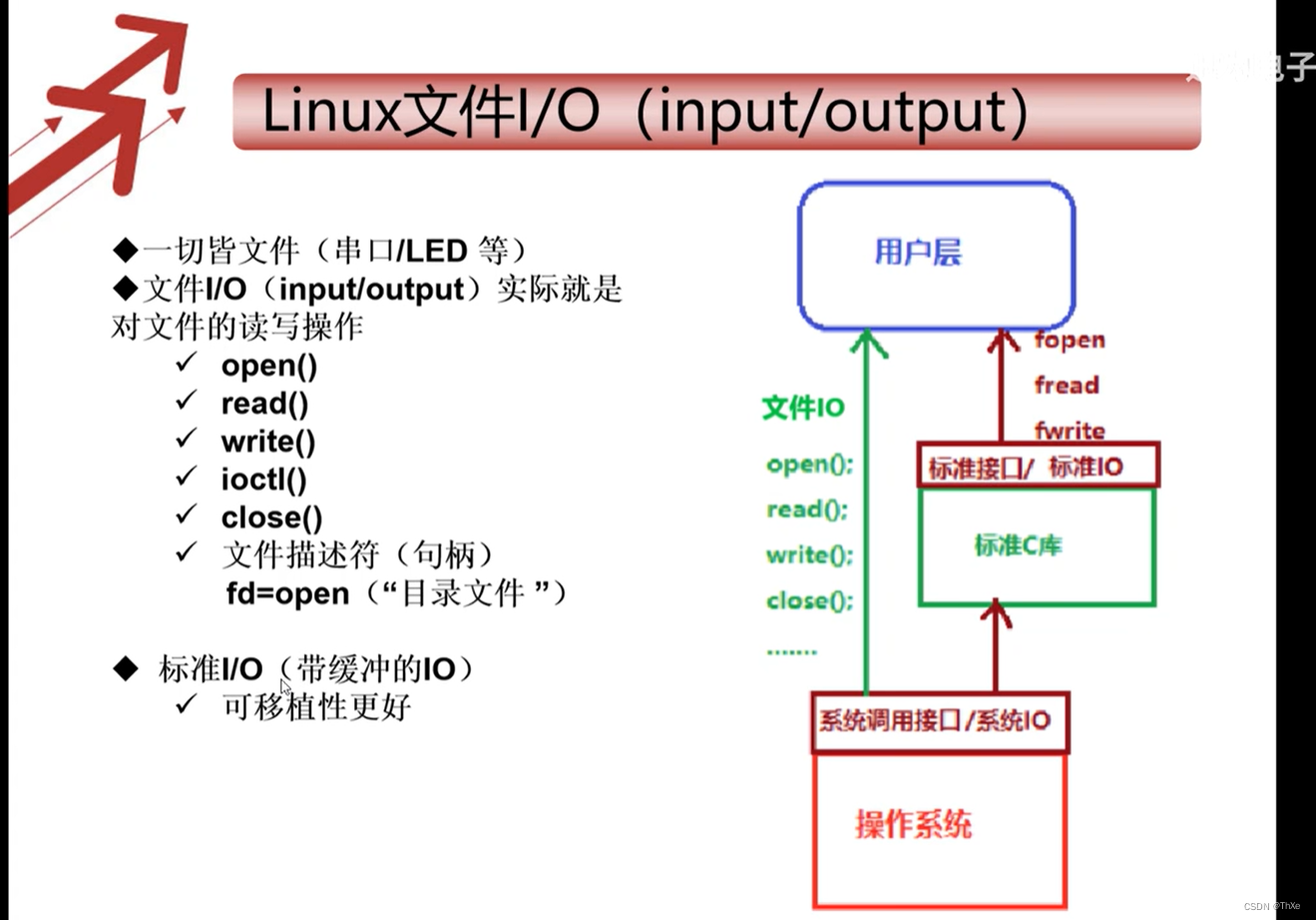
Platform Driver (1) Linux kernel中大部分设备可以归结为平台设备,因此大部分的驱动是平台驱动(patform driver) 什么是平台设备 平台设备是linux的设备模型中一类设备的抽象。 内核中的描述: Platform devices are devices t…...

开发手册——一、编程规约_7.控制语句
这篇文章主要梳理了在java的实际开发过程中的编程规范问题。本篇文章主要借鉴于《阿里巴巴java开发手册终极版》 下面我们一起来看一下吧。 1. 【强制】在一个 switch 块内,每个 case 要么通过 break / return 等来终止,要么注释说明程序将继续执行到哪…...
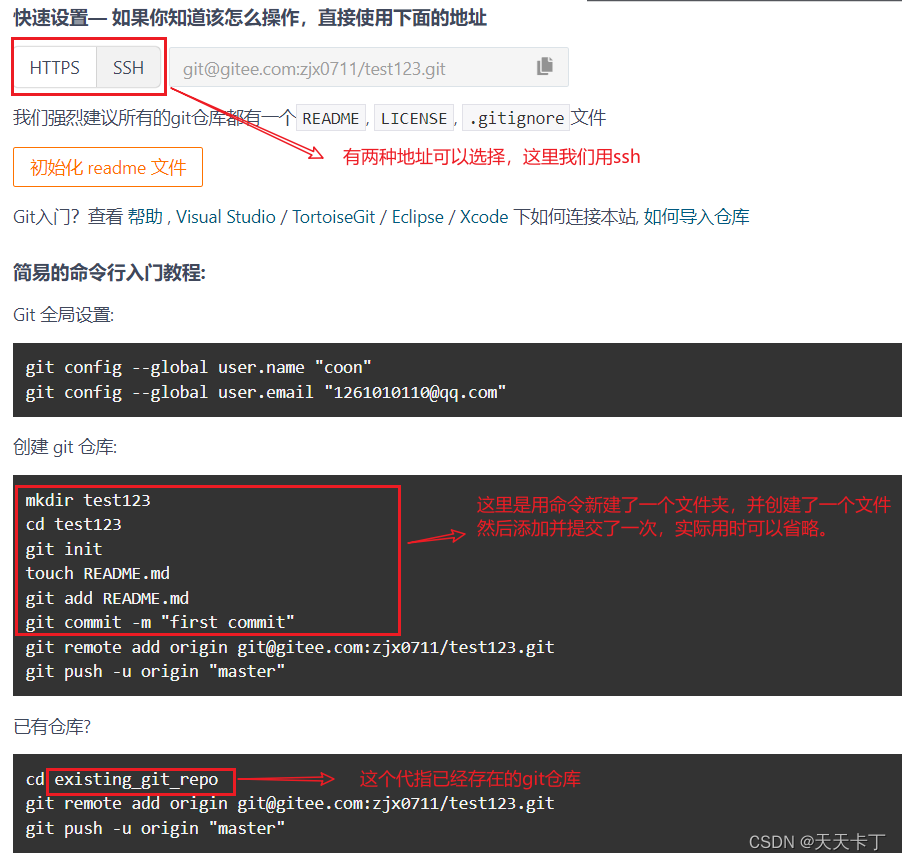
python每日学9 : windows上配置gitee的远程仓库,git的初步使用
在开发中,如果遇到复杂的项目,使用版本控制是非常有必要的,如果涉及到多端开发,那么还需要使用远程仓库。本文作个简单记录,记录下git初步使用。 1 下载与安装 git还有几个ui版本,但是开始使用的话&#…...
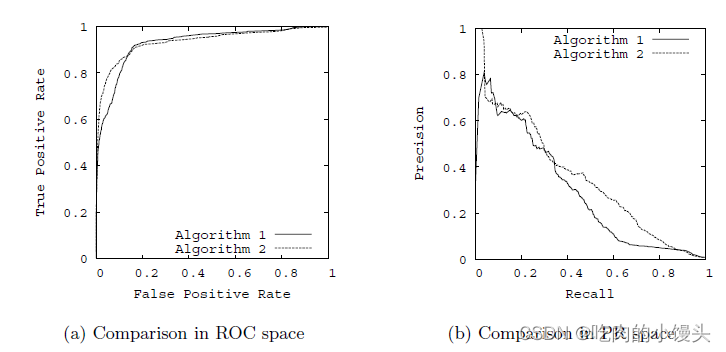
精确率与召回率,ROC曲线与PR曲线
精确率与召回率,ROC曲线与PR曲线 在机器学习的算法评估中,尤其是分类算法评估中,我们经常听到精确率(precision)与召回率(recall),ROC曲线与PR曲线这些概念,那这些概念到底有什么用处呢? 首先,…...
现代操作系统——Linux架构与学习
小白的疑惑 在我决定从事嵌入式(应用层)方面的工作时,我查询了大量资料该如何学习,几乎所有观点不约而同的都指向了学习好Linux,大部分工作都是在Linux环境下来进行工作的。于是我雄心勃勃的去下载Linux,可…...

中文代码82
PK 嘚釦 docProps/PK 嘚釦羸 r docProps/app.xml潙蚽?勶曻Q顗濔S? 錞礖剅D柍珘m?鳞?ぷ辷f硌?2?upc厭Y樐8 rU y搪m眾&a?珪?紓 玺鶋瑣襚? ?i嘲rN?布倖儇?攊橌??嚗猝)芻矂2吟腊K湞?CK臶>鸘\?ΔF滋齢q旮T?桀?;偉 A軥v蕯朾偤佷3?е…...
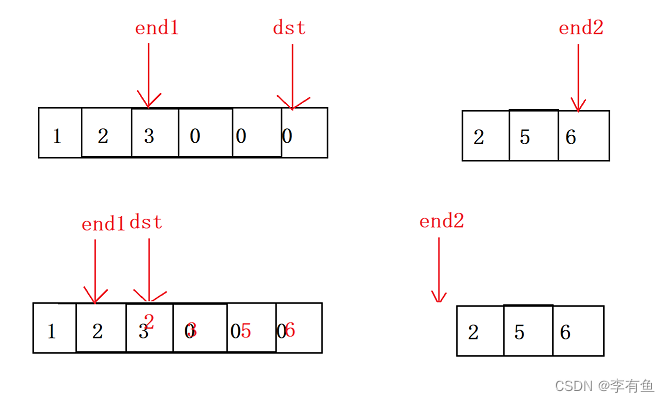
顺序表(一篇带你掌握顺序表)
目录 一、顺序表是什么 1.1 概念 1.2 分类 1.3 结构 二、顺序表的基本操作 2.1 前绪准备 2.2 初始化 2.3 扩容 2.5 尾插 2.6 打印 2.7 尾删 2.8 头插 2.9 头删 2.10 在pos位置插入 2.11 删除pos位置的数据 2.12 查找 三、完整代码 3.1 Test.c文件 3.2 SeqList.h…...
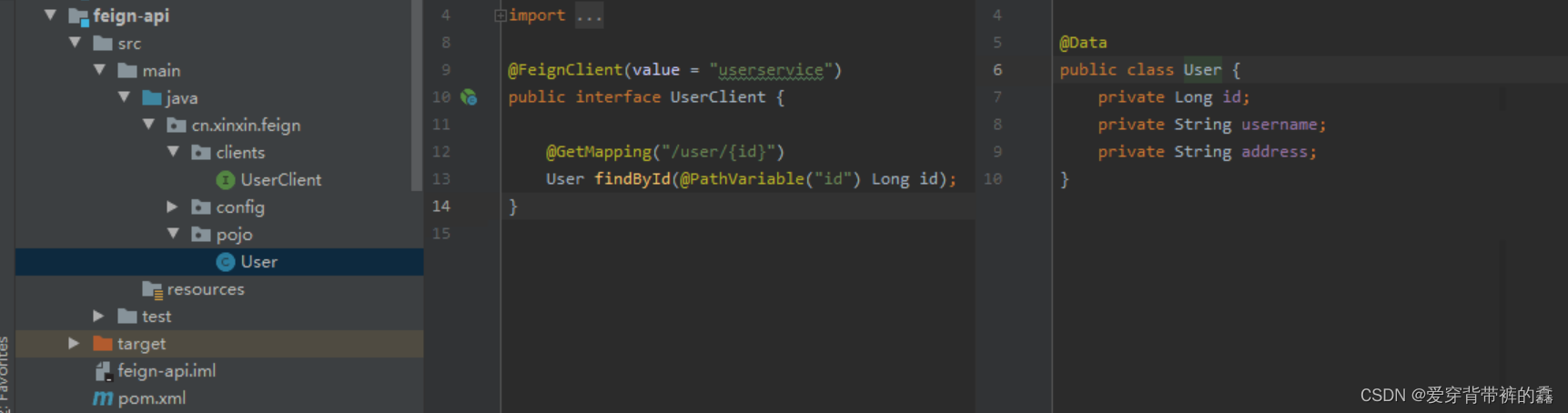
【SpringCloud】SpringCloud教程之Feign实战
目录前言SpringCloud Feign远程服务调用一.需求二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用(order服务内编写)四.构建Feign(order服务内配置)五.自定义Feign配置(order服务内配置)六.Feign配置日志(oder服务内配置)七.Feign调优(order服务内配置)八.抽离Feign前…...
嵌入式linux必备内存泄露检测神器
Valgrind介绍 Valgrind是一个可移植的动态二进制分析工具集,主要用于发现程序中的内存泄漏、不合法内存访问、使用未初始化的内存、不正确的内存释放以及性能问题等,可在Linux和Mac OS X等平台上使用。 Valgrind由多个工具组成,其中最常用的…...

设计模式之行为型模式
四、行为型模式 行为型模式用于描述程序在运行时复杂的流程控制,即描述多个类或对象之间怎样相互协作共同完成单个对象都无法单独完成的任务,它涉及算法与对象间职责的分配。 行为型模式分为类行为模式和对象行为模式,前者采用继承机制来在…...

解密 三岁的三岁到底为什么叫做三岁?
机缘 那一年,一次奇奇怪怪的挫折与一次奇奇怪怪的成长。 在学习Python的路上总觉得少了点什么,是心情?是机遇?还是力量? 都不是又都是! 缺少一个实践和记忆的平台 记性不好是硬伤 前一天学的下一秒就忘记了…...

id选择器
id选择器可以为特定的id的标签进行css美化 使用方法: 标签内设好 id值, CSS的id选择器以“#id名”来调用 注意 所有标签都有id值id属性值类似于身份证号码,在一个页面中是唯一的值,不可重复一个标签上只能有一个id属性值一个id属性…...

《科技之巅3》读书笔记
文章目录书籍信息人工智能,“吃一堑长一智”的机器人机交互,为解决“交流障碍”问题而生硬件与算法,好马还需好鞍模式创新,赋予技术新的定义云与数据共享,灵活应对信息的爆发式增长“机器人”,从电影和小说…...
18.用于大型程序的工具
文章目录用于大型程序的工具18.1异常处理18.1.1抛出异常栈展开栈展开过程中对象被自动销毁析构函数与异常异常对象18.1.2捕获异常查找匹配的处理代码重新抛出捕获所有异常的处理代码18.1.3函数try语句块与构造函数18.1.4noexcept异常说明违反异常说明异常说明的实参noexcept运算…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
