动态规划最后一天(回文串)
目录
647. 回文子串
看到题目的第一想法
看到代码随想录之后的想法
自己实现过程中遇到的困难(看代码)
516.最长回文子序列
看到题目的第一想法
看到代码随想录之后的想法
自己实现过程中遇到的困难(看代码)
647. 回文子串
力扣题目链接(opens new window)
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
- 输入:"abc"
- 输出:3
- 解释:三个回文子串: "a", "b", "c"
示例 2:
- 输入:"aaa"
- 输出:6
- 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:输入的字符串长度不会超过 1000 。
看到题目的第一想法
按照回溯来做,没做出来,没法用回溯来写
使用暴力可以解
使用dp 将数目记录,但是递推公式不好计算
看到代码随想录之后的想法
用动态规划,若i==j 则看i和j之间是否是回文串,如果是回文则dp[i][j]也是回文
(选中两个单词的字符,若相同看中间是否是回文)
确定dp数组和每个下标的含义
dp[i][j],看i和j之间是否是回文串
确定递推公式
若s[i]==s[j] 则有三种情况
若i==j 则dp[i][j]=true
若i=j-1 则dp[i][j]=true
若i>j-1,则dp[i][j] = dp[i+1][j-1](看i,j中间的是否是回文串)
dp数组初始化
初始化都为false,相当于遍历时若为回文则改为true
确定遍历顺序
dp[i][j] 依赖于 dp[i+1][j-1] 则可以从下往上,从左往右进行遍历
举例推导dp数组
打印dp数组
遍历时记录true的个数,返回总数,就是回文子串的个数了
自己实现过程中遇到的困难(看代码)
回溯没写出来
第一时间想一下暴力
回文串记得通过[i,j]中间的来进行判断
class Solution {public int countSubstrings(String s) {//我的思路是记录回文子串数目,其中dp数组是不太好推测的//卡哥的思路是,利用dp[i][j]二维数组,看[i,j] 是否是回文子串//若为回文子串则为true ,若不为则为false//若 s[i] s[j]相等,那么我们可以看[i+1][j-1] 是否为回文子串,若为回文,则dp[i][j]也为回文(相当于包在里面)//确定dp数组和下标的含义// dp[i][j] 看[i,j]是否为回文子串,若是则为true,否则为false//确定递推公式// 若s[i]=s[j] 有三种情况 1 i==j 则直接为true// 2 i==j-1 则直接为true// 3 i<j-1 则需要判断 若dp[i+1][j-1]==true 则dp[i][j]为true//dp数组初始化//全都为false ,先默认都不为回文子串,然后再一个个改成回文子串//确定遍历顺序//dp[i][j]依赖于dp[i+1][j-1],则从下往上,从前往后//举例推导dp数组int result = 0;boolean[][] dp = new boolean[s.length()][s.length()];for(int i=s.length()-1;i>=0;i--){for(int j=i;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){if(i==j||i==j-1||dp[i+1][j-1]==true){dp[i][j] = true;result++;}}}}return result;}
}//我的想法,用回溯?判断是否回文,是则加入result中//回溯算法三要素//回溯函数的参数和返回值//字符串以及startIndex//回溯函数的终止条件//若字符串到最后则返回//回溯函数的执行逻辑//若startIndex到i为回文串则加入到结果集中//正着读和倒着读一样的字符串//dp[i][j] 遍历到[i-1,j-1]里面回文子串的数目,// 确定递推公式// 若[i-1,j-1]为回文子串,则dp[i][j] = Math.max(dp[i-1][j]+1,dp[i][j-1]+1)// 若[i-1,j-1]不为回文子串,dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);// dp数组初始化// 都为0// 确定遍历顺序// 从上往下从左至右/*int[][] dp = new int[s.length()+1][s.length()+1];for(int i=1;i<=s.length();i++){for(int j=i;j<=s.length();j++){if(isValid(s,i-1,j-1)){dp[i][j] = Math.max(dp[i-1][j]+1,dp[i][j-1]+1);}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}/return dp[s.length()][s.length()];//backTracking(s,0);//return resultPath.size();}boolean isValid(String s,int i,int j){//判断是否是回文while(i<j){if(s.charAt(i)!=s.charAt(j)){return false;}i++;j--;}return true;}/*void backTracking(String s,int startIndex){if(startIndex==s.length()){return ;}for(int i=startIndex;i<s.length();i++){if(isValid(s,startIndex,i)){String sub = s.substring(startIndex,i+1);if(isValid(sub)){resultPath.add(sub);}}else{continue;}backTracking(s,startIndex+1); }}boolean isValid(String s){//判断是否是回文int i=0;int j=s.length()-1;while(i<j){if(s.charAt(i)!=s.charAt(j)){return false;}i++;j--;}return true;}*/
//}
516.最长回文子序列
力扣题目链接(opens new window)给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1: 输入: "bbbab" 输出: 4 一个可能的最长回文子序列为 "bbbb"。
示例 2: 输入:"cbbd" 输出: 2 一个可能的最长回文子序列为 "bb"。
看到题目的第一想法
dp[i][j]记录所有和i相等的j 的个数当成回文串
写出来发现不符合题意,比如说aabaa也是回文串,但是a的个数为4 ,串长度为5
求的是串的长度
看到代码随想录之后的想法
用动态规划,若i==j 则看i和j之间回文串的最大长度
(选中两个单词,看中间回文串的最大长度)
确定dp数组和每个下标的含义
dp[i][j],看i和j之间回文串的最大长度
确定递推公式
若s[i]==s[j] 则dp[i][j] = dp[i+1][j-1]+2
若s[i]!=s[j] 看选中其中一个字符的最长回文是多少,则
dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
dp数组初始化
当i==j时,一定时回文,全都初始化为1
确定遍历顺序
dp[i][j] 依赖于 dp[i+1][j-1] 则可以从下往上,从左往右进行遍历
举例推导dp数组
打印dp数组
遍历时记录true的个数,返回总数,就是回文子串的个数了
自己实现过程中遇到的困难(看代码)
理解一下回文的含义
回文串记得通过[i,j]中间的来进行判断,相等时不要忘了dp[i+1][j-1] +2
做的时候忘了+2了
class Solution {public int longestPalindromeSubseq(String s) {//卡哥的思路//dp[i][j] 记录[i~j]的最长的回文子序列//确定递推公式//若s[i]==s[j] 则看两者间最长的回文子序列是多少 dp[i][j] = dp[i+1][j-1]+2 加了两个字符,所以加2//若s[i]!=s[j] 则看选中s[i] 于选中s[j]的两个序列中,最长的回文子序列是多少(两者的最大值)// dp[i][j] = max(dp[i+1][j],dp[i][j-1])//确定遍历顺序//由于dp依赖于dp[i+1][j-1]则dp[i][j]遍历顺序为由下往上,从左往右//dp数组初始化//当i==j时一定是回文,所以dp[i][i]=1int[][] dp = new int[s.length()][s.length()];for(int i=0;i<s.length();i++){dp[i][i]=1;}for(int i=s.length()-2;i>=0;i--){for(int j=i+1;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){dp[i][j] = dp[i+1][j-1]+2;}else{dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);}}}//返回0~length-1的最大值return dp[0][s.length()-1];/*//我的思路:和之前那道题思路一样? 想着所有和i相等的都是回文,其实是错误的比如bbabb 回文长度为5 我为4//若i==j dp[i][j] = dp[i][j-1]+1 //若i!=j dp[i][j] = dp[i][j-1]//确定dp的参数和下标的含义//i-1~j-1之间以i开头最长的子序列的长度//确定递推公式//若s[i-1]==s[j-1] dp[i][j] = dp[i][j-1]+1//若s[i-1]!=s[j-1] dp[i][j] = dp[i][j-1]//dp数组初始化//默认为0//确定遍历顺序//从上往下,从左至右//举例推导dp数组int[][] dp = new int[s.length()+1][s.length()+1];int max = 0;for(int i=1;i<s.length()+1;i++){for(int j=i;j<s.length()+1;j++){if(s.charAt(i-1)==s.charAt(j-1)){dp[i][j] = dp[i][j-1]+1;if(dp[i][j]>max){max = dp[i][j];}}else{dp[i][j] = dp[i][j-1];}}}return max;*/}
}相关文章:
)
动态规划最后一天(回文串)
目录 647. 回文子串 看到题目的第一想法 看到代码随想录之后的想法 自己实现过程中遇到的困难(看代码) 516.最长回文子序列 看到题目的第一想法 看到代码随想录之后的想法 自己实现过程中遇到的困难(看代码) 647. 回文子串 力扣题目链接…...

c语言之scanf函数
scanf函数语法格式与printf函数很相似,语法是scanf(格式控制,地址列表)组成 其中格式控制分为两部分,一部分由双引号括起来的,%和格式字符组成的格式字符串 普通字符串则是原样输出 地址列表是若干地址组成的表列,可以是变量的…...

ORM-02-JPA Java Persistence API 注解入门介绍
拓展阅读 The jdbc pool for java.(java 手写 jdbc 数据库连接池实现) The simple mybatis.(手写简易版 mybatis) JPA JPA是Java Persistence API的简称,中文名Java持久层API,是JDK 5.0注解或XML描述对象-关系表的映射…...

【MQ01】什么是消息队列?用哪个消息队列?
什么是消息队列?用哪个消息队列? 来了来了,消息队列系列总算来咯。对于搜索引擎相关的知识大家消化的怎么样呀?其实对于搜索引擎来说,我们学习的内容还是挺全面的,也算是比较深入了。而对于消息队列来说&am…...

2023年度AI盘点 AIGC|AGI|ChatGPT|人工智能大模型
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 2023年是人工智能大语言模型大爆发的一年,一些概念和英文缩写也在这一年里集中出现,很容易混淆,甚至把人搞懵。 文章目录 前言01 《ChatGPT 驱动软件开…...
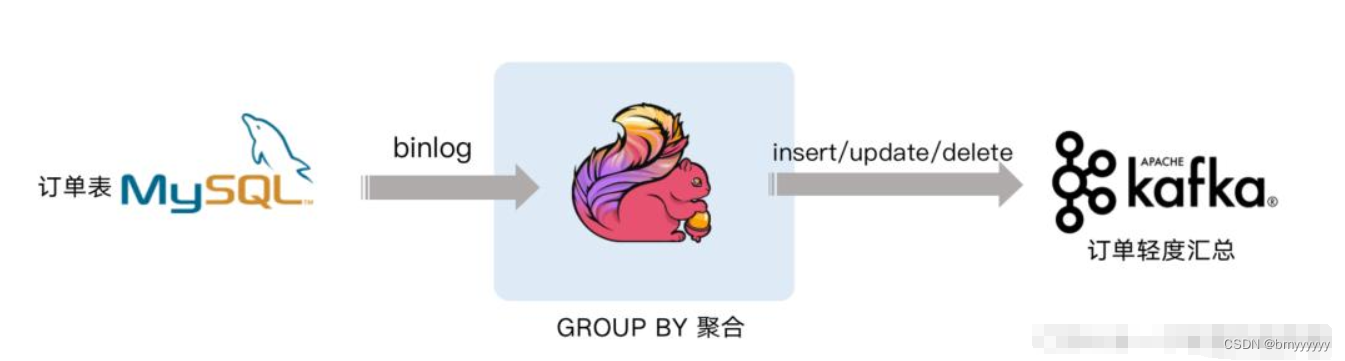
【Flink-CDC】Flink CDC 介绍和原理概述
【Flink-CDC】Flink CDC 介绍和原理概述 1)基于查询的 CDC 和基于日志的 CDC2)Flink CDC3)Flink CDC原理简述4)基于 Flink SQL CDC 的数据同步方案实践4.1.案例 1 : Flink SQL CDC JDBC Connector4.2.案例 2 : CDC Streaming ETL…...

长城资产信息技术岗24届校招面试面经
本文介绍2024届秋招中,中国长城资产管理股份有限公司的信息技术岗岗位一面的面试基本情况、提问问题等。 10月投递了中国长城资产管理股份有限公司的信息技术岗岗位,所在部门为长城新盛信托有限责任公司。目前完成了一面,在这里记录一下一面经…...
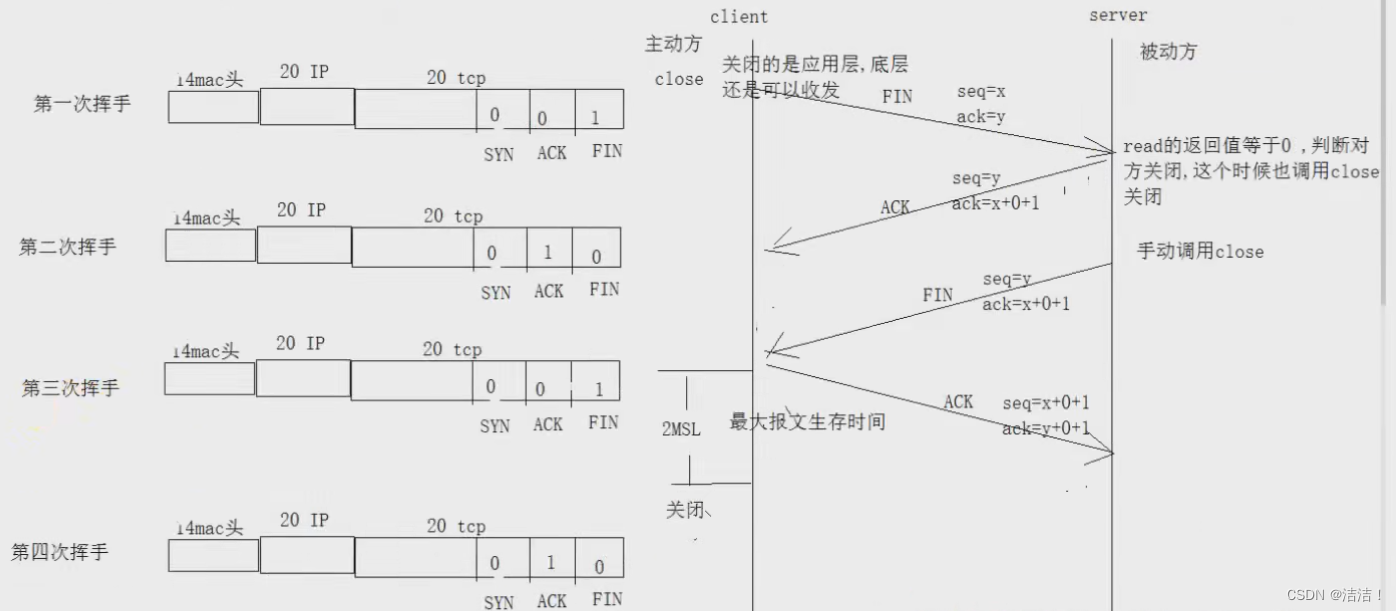
【计算机网络】TCP握手与挥手:三步奏和四步曲
这里写目录标题 前言三次握手四次挥手三次握手和四次挥手的作用TCP三次握手的作用建立连接防止已失效的连接请求建立连接防止重复连接 TCP四次挥手的作用:安全关闭连接避免数据丢失避免半开连接 总结: 总结 前言 TCP(传输控制协议)…...

设计模式学习总结
责任链模式 使用方法: 1.创建接口 2.定义实现类,每个实现类实现接口,并拥有一个ArchiveHandle的成员,用作责任链的链接 public interface ArchiveHandle {void handle(ArchiveVO archiveVO); } public class ArchivePreHandle i…...

「HDLBits题解」Cellular automata
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 题目链接:Rule90 - HDLBits module top_module(input clk,input load,input [511:0] data,output [511:0] q );always (posedge clk) begin…...

什么是API ?
API(应用程序编程接口) 就像现成的家具套件相对于家居建设,用一些已经切好的木板组装一个书柜,显然比自己设计,寻找合适的木材,裁切至合适的尺寸和形状,找到正确尺寸的螺钉,然后再组…...

Pytest中conftest.py的用法
Pytest中conftest.py的用法 在官方文档中,描述conftest.py是一个本地插件的文件,简单的说就是在这个文件中编写的方法,可以在其他地方直接进行调用。 注意事项 只能在根目录编写conftest.py 插件加载顺序在搜集用例之前 基础用法 这里…...

java.lang.IllegalArgumentException: When allowCredentials is true
1.遇到的错误 java.lang.IllegalArgumentException: When allowCredentials is true, allowedOrigins cannot contain the special value "*" since that cannot be set on the "Access-Control-Allow-Origin" response header. To allow credentials to a…...

vue折叠展开transition动画使用keyframes实现
需求,我正常的菜单功能有隐藏与显示功能,需要增加动画 打开的时候宽度从0到300,关闭的时候,宽度从300到0 <template> <div id"app"> <button click"toggleLength">Toggle Length</bu…...
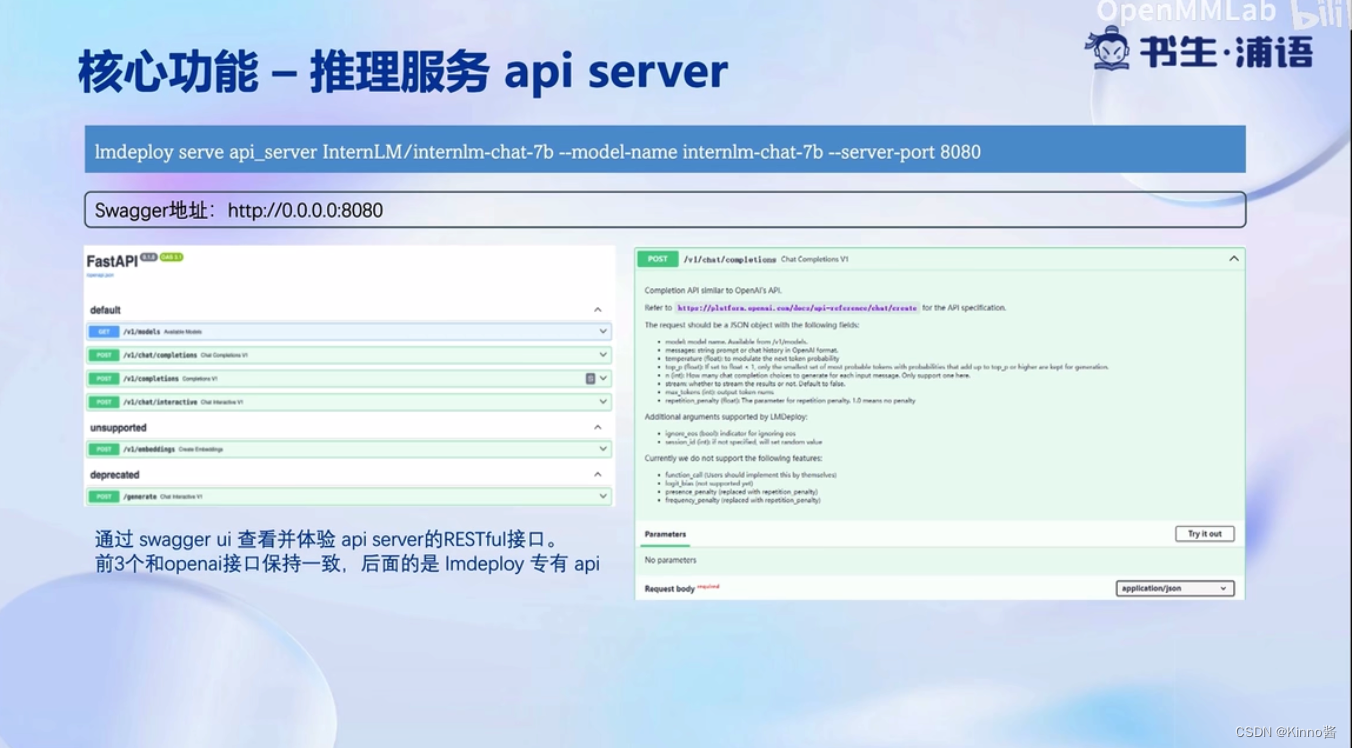
书生·浦语大模型实战营-学习笔记5
LMDeploy 大模型量化部署实践 大模型部署背景 LMDeploy简介 轻量化、推理引擎、服务 核心功能-量化 显存消耗变少了 大语言模型是典型的访存密集型任务,因为它是decoder-by-decoder 先把数据量化为INT4存起来,算的时候会反量化为FP16 AWQ算法&a…...
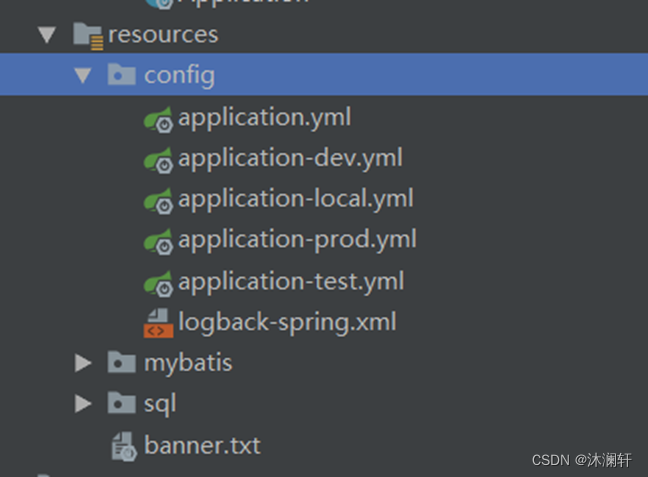
10. Profile
1. 区分环境的配置 1.1. properties 配置 假设,一个应用的工作环境有:dev、test、prod 那么,我们可以添加 4 个配置文件: applcation.properties - 公共配置application-dev.properties - 开发环境配置application-test.proper…...

YOLO 自己训练一个模型
一、准备数据集 我的版本是yolov8 8.11 这个目录结构很重要 ultralytics-main | datasets|coco|train|val 二、训练 编写yaml 文件 # Train/val/test sets as 1) dir: path/to/imgs, 2) file: path/to/imgs.txt, or 3) list: [path/to/imgs1, path/to/imgs2, ..] path…...
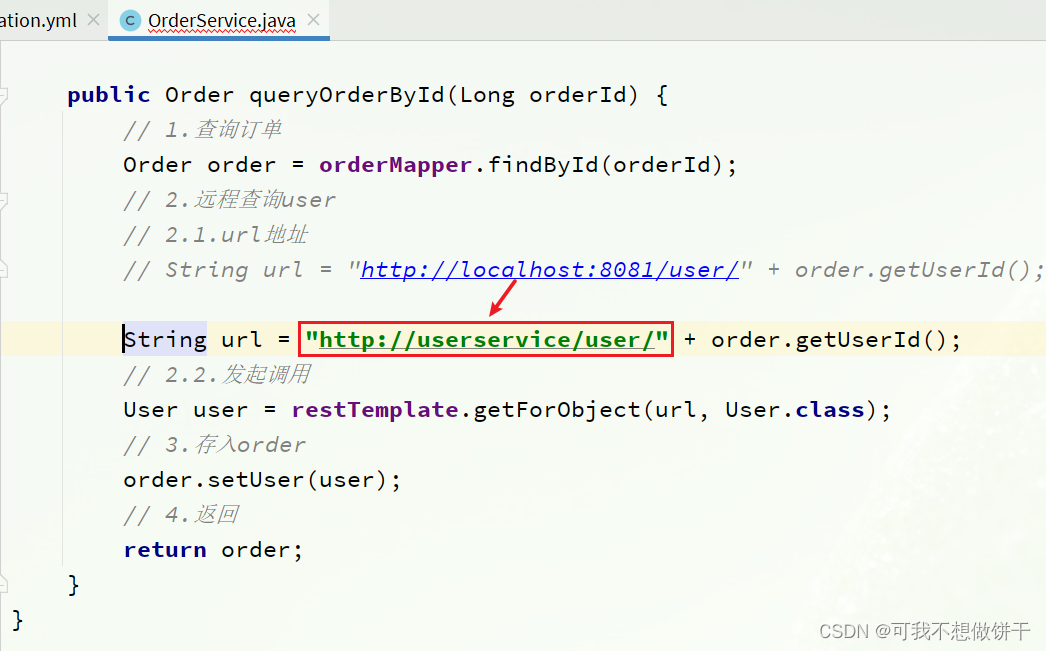
3.Eureka注册中心
3.Eureka注册中心 假如我们的服务提供者user-service部署了多个实例,如图: 大家思考几个问题: order-service在发起远程调用的时候,该如何得知user-service实例的ip地址和端口?有多个user-service实例地址࿰…...

基于springboot+vue的墙绘产品展示交易平台系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 研究背景…...
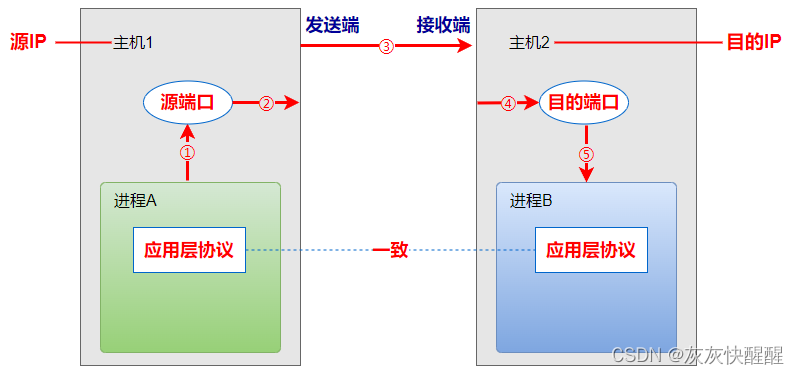
网络原理-初识(1)
目录 网络发展史 独立模式 网络互连 局域网LAN 广域网WAN 网络通信基础 IP地址 概念 格式 端口 概念 格式 认识协议 概念 作用 五元组 网络发展史 独立模式 独立模式:计算机之间相互独立; 网络互连 随着时代的发展,越来越需要计算机之间相互通信,共享软件和数…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
