十大排序(C++版)
测试排序的题目:
912. 排序数组 - 力扣(LeetCode)
堕落的做法:
class Solution
{
public:vector<int> sortArray(vector<int>& nums) {sort(nums.begin(),nums.end());return nums;}
};
视频推荐:
91.基数排序的原理_哔哩哔哩_bilibili
代码推荐:
【C++】十大排序(冒泡、选择、插入、希尔、归并、快排、堆、计数、桶、基数) - 排序数组 - 力扣(LeetCode)
文章目录
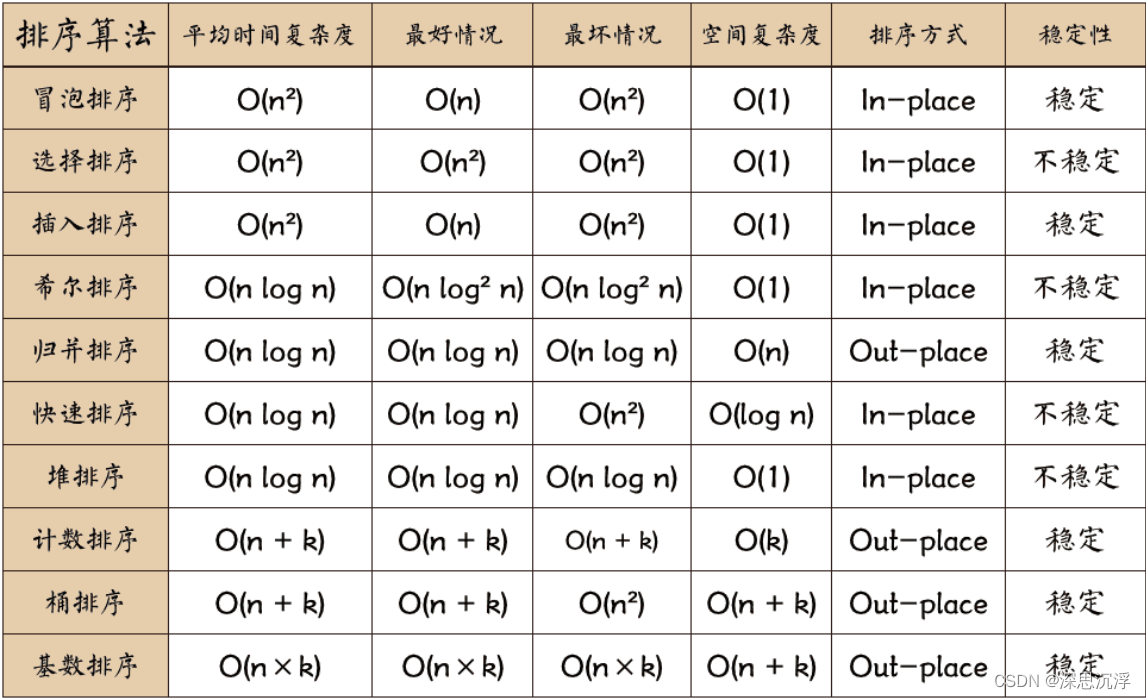
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序、
- 归并排序
- 快速排序
- 堆排序
- 计数排序
- 桶排序
- 基数排序
冒泡排序
- 算法步骤:
- 比较相邻的元素:若第一个比第二个大,则交换;
- 遍历开始第一对到结尾最后一对,执行步骤
1; - 重复步骤
1~2,直到排序完成。
class Solution
{
public:vector<int> sortArray(vector<int>& nums) {int n = nums.size();for (int i = 0; i < n - 1; ++i) {bool flag = false;for (int j = 0; j < n - 1 - i; ++j) {if (nums[j] > nums[j + 1]) {swap(nums[j], nums[j + 1]);flag = true;} }if (flag == false) break; //优化点:无交换代表已经排好序了}return nums;}
};
注意:本题中使用冒泡排序过不去,会超时
选择排序
- 算法步骤:
- 初始状态:无序序列为R[0,n−1],长度n,有序区为空;
- 第i=1,…,n−1趟排序从当前无序区R[i−1,n−1]中选出最小的元素R[k],并将它与无序区的第1个记录R[i−1]交换,则R[0,i−1]变为元素个数增加1的新有序区,R[i,n−1]变为元素个数减少1的新无序区;
- n−1趟选择交换后结束。
class Solution
{
public:vector<int> sortArray(vector<int>& nums){int n = nums.size();for (int i = 0; i < n; i++){int minindex = i;for (int j = i + 1; j < n; j++){if (nums[j] < nums[minindex]) minindex = j;}swap(nums[i], nums[minindex]);}return nums;}
};
注意:本题中使用选择排序过不去,会超时
插入排序
- 算法步骤:
- 从第一个元素开始,该元素认为已经被排序;
- 取下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果已排序元素大于新元素,将已排序元素移到下一位置;
- 重复步骤
3,直到找到已排序的元素小于或者等于新元素的位置; - 将新元素插入到该位置后;
- 重复步骤
2~5。
普通版本:
class Solution
{
public:vector<int> sortArray(vector<int>& nums){int n = nums.size();for (int i = 1; i < n; i++){int currnumber = nums[i];int j = i - 1;for (; j >= 0; j--){if (nums[j] >= currnumber) swap(nums[j], nums[j + 1]);else break;}swap(currnumber, nums[j + 1]);}return nums;}
};
时间复杂度:最好O(n)最坏O(n^2)
空间复杂度:O(1)
希尔排序、
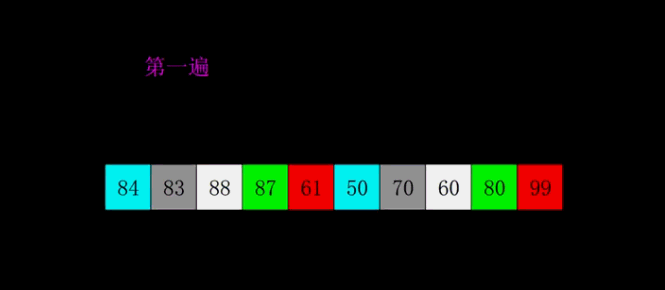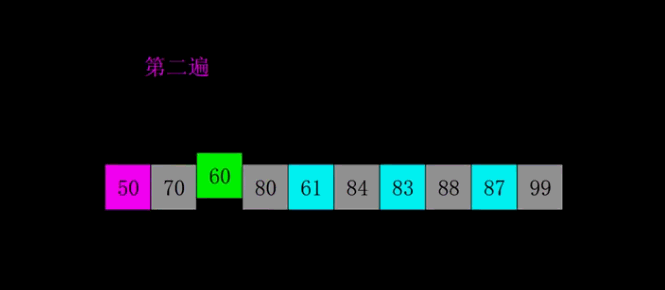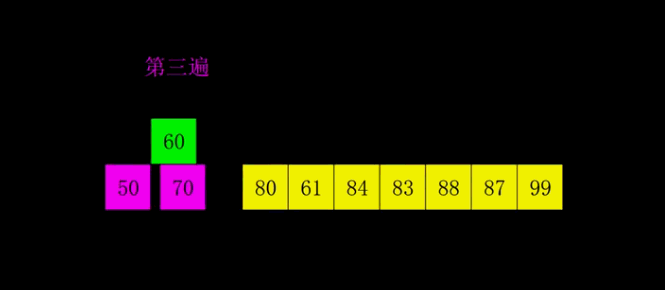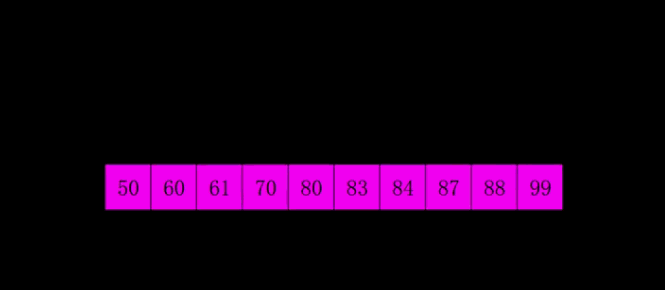
- 算法步骤:
- 选择一个增量序列T1,T2,… ,Tk,其中Ti>Tj,Tk=1,i>j;
- 每趟排序,根据对应的增量Ti,将待排序列分割成若干子序列,分别对各子序列进行直接插入排序;
- 按增量序列个数k,对序列进行k趟排序。
class Solution
{
public:vector<int> sortArray(vector<int>& nums) {int n = nums.size();// 分组,最开始时,间隔T为数组的一半for (int T = n / 2; T >= 1; T /= 2) {//对分组进行插入排序for (int i = T; i < n; ++i){shellSort(nums, T, i);}}return nums;}void shellSort(vector<int>& nums, int T, int i) {int j, tmp = nums[i];for (j = i - T; j >= 0 && tmp < nums[j]; j -= T) {nums[j + T] = nums[j];}nums[j + T] = tmp;}
};
第一个通过的排序
归并排序
- 算法步骤:
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
class Solution
{
public:vector<int> sortArray(vector<int>& nums){res.resize(nums.size(), 0);MerageSort(nums, 0, nums.size() - 1);return nums;}void MerageSort(vector<int>& nums, int left, int right){if (left >= right) return;int mid = (left + right) / 2;MerageSort(nums, left, mid);MerageSort(nums, mid + 1, right);int l = left, r = mid + 1, i = left;while (l <= mid && r <= right){if (nums[l] < nums[r]) res[i++] = nums[l++];else res[i++] = nums[r++];}while (l <= mid) res[i++] = nums[l++];while (r <= right) res[i++] = nums[r++];for (int i = left; i <= right; i++) nums[i] = res[i];}
private:vector<int> res;
};
归并排序最好情况下:O(nlogn),最坏情况下 O(nlogn),归并排序的空间复杂度 O(n),如果使用的是堆上空间,则操作时间可能更长(分配销毁时间太长)
快速排序
算法步骤:
- 从数列中挑出一个元素,称为
基准pivot; - 分区
partition操作:比基准值小的元素放在左边,比基准值大的元素放在右边; - 递归
recursive:把小于基准值元素的子数列和大于基准值元素的子数列分别递归排序。
普通的快排(选取中间点):
class Solution
{
public:vector<int> sortArray(vector<int>& nums){QuickSort(nums, 0, nums.size() - 1);return nums;}void QuickSort(vector<int>& nums, int left, int right){if (left >= right) return;int x = nums[(left + right) / 2], l = left - 1, r = right + 1;while (l < r){do l++; while (nums[l] < x);do r--; while (nums[r] > x);if (l < r) swap(nums[l], nums[r]);}QuickSort(nums, left, r);QuickSort(nums, r + 1, right);}
};
优化后的快排(随机选点)
class Solution
{
public:vector<int> sortArray(vector<int>& nums){QuickSort(nums, 0, nums.size() - 1);return nums;}void QuickSort(vector<int>& nums, int left, int right){if (left >= right) return;int x = nums[rand() % (right - left + 1) + left], l = left - 1, r = right + 1;while (l < r){do l++; while (nums[l] < x);do r--; while (nums[r] > x);if (l < r) swap(nums[l], nums[r]);}QuickSort(nums, left, r);QuickSort(nums, r + 1, right);}
};
**rand() % (b-a+1)+ a ** 就表示 a~b 之间的一个随机整数。
快速排序最好情况下:O(nlogn) ,最坏情况下退化为选择排序(例如每次选择的都是最大值,之后遍历左边的 n -1 序列):O(n^2)
堆排序

- 算法步骤:
- 将初始待排序关键字序列
(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区; - 将堆顶元素
R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]; - 由于交换后新的堆顶
R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
- 将初始待排序关键字序列

class Solution
{
public:vector<int> sortArray(vector<int>& nums) {// heapSort 堆排序int n = nums.size();// 将数组整理成大根堆buildMaxHeap(nums);for (int i = n - 1; i >= 1; --i) {// 依次弹出最大元素,放到数组最后,当前排序对应数组大小 - 1swap(nums[0], nums[i]);--n;maxHeapify(nums, 0, n);}return nums;}void buildMaxHeap(vector<int>& nums){int n = nums.size();for (int i = (n - 1) / 2; i >= 0; --i)//从最后一个节点的父节点开始进行堆排序{maxHeapify(nums, i, n);}}void maxHeapify(vector<int>& nums, int i, int n){while (i * 2 + 1 < n){// 代表当前 i 节点的左右儿子;// 超出数组大小则代表当前 i 节点为叶子节点,不需要移位int lSon = 2 * i + 1;int rSon = 2 * i + 2;int large = i;if (lSon < n && nums[lSon] > nums[i]) large = lSon;if (rSon < n && nums[rSon] > nums[large]) large = rSon;if (large != i){swap(nums[i], nums[large]);// 迭代判断对应子节点及其儿子节点的大小关系i = large;}else//若当前根节点和左右节点和维持大根堆则跳出循环{break;}}}
};
什么是堆?堆有哪些特征?
堆是一个可以被看做一棵树的数组对象, 它的形状特征是完全二叉树且是顺序存储,数值特征:根总是优于左孩子和右孩子。
堆中的父结点和孩子结点的下标有什么特征
若 pos 是父亲节点下标(其节点编号是 pos + 1),左孩子的下标就是 2pos +1,右孩子是 2pos + 2
简述堆排序的流程:
1、对N个无序元素的数组简历大根堆
从最后一个父亲节点开始,向前循环
先比较左右孩子,再用胜者与父亲比较,如果孩子胜利,交换父亲和孩子,再重复检查交换后原父亲的稳定性。
2、交换堆顶和末尾元素,缩小堆的规模,从新的根节点出发,重建堆。
3、循环步骤2,堆的规模从n到2.
计数排序
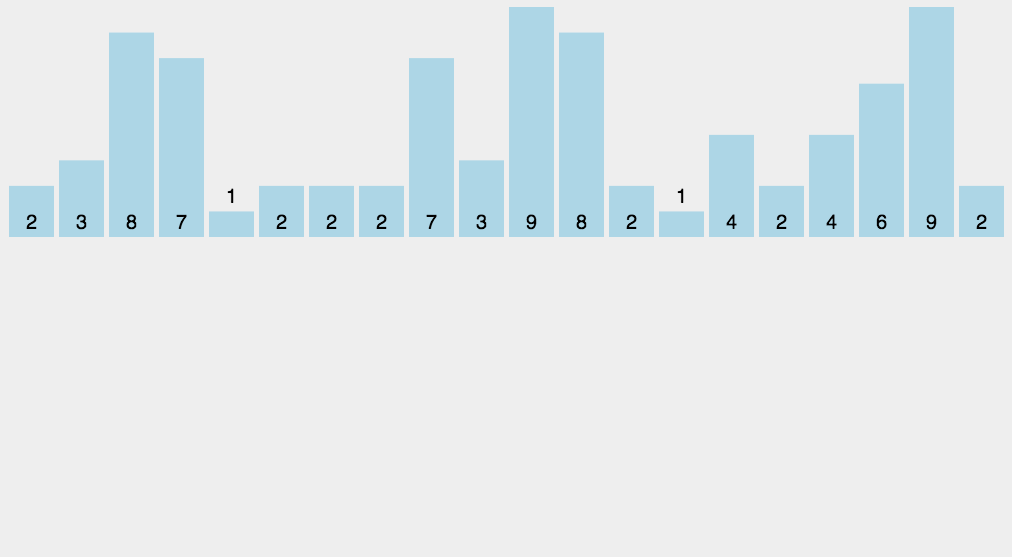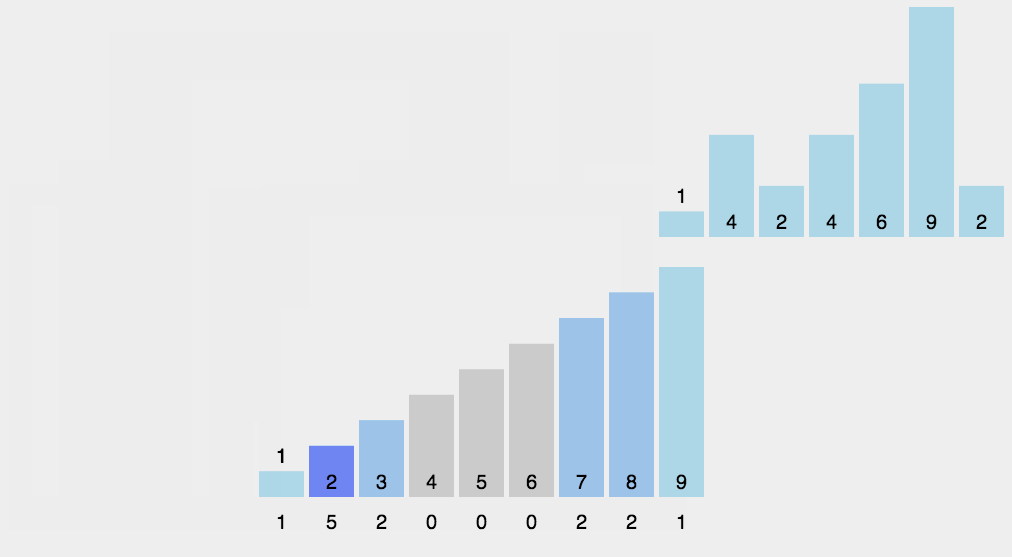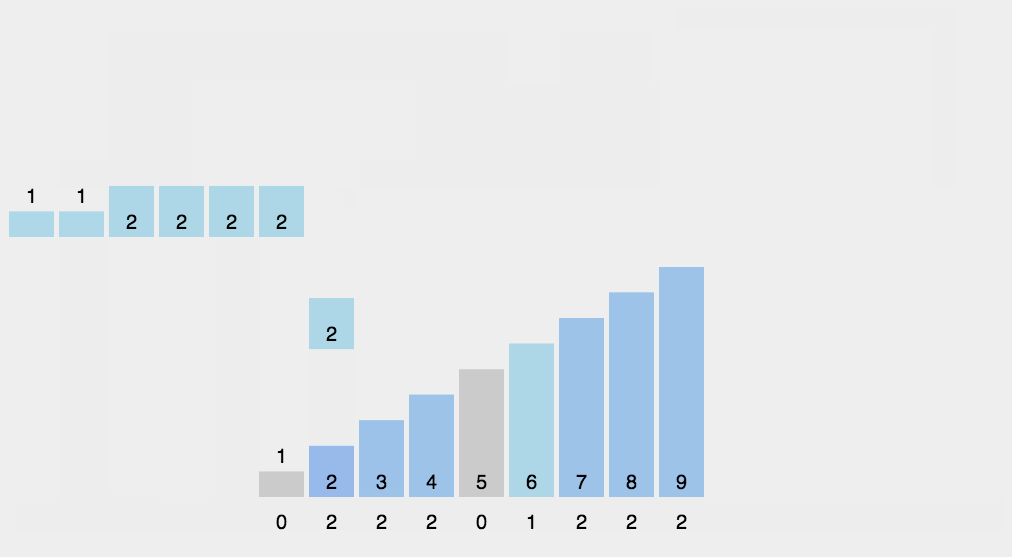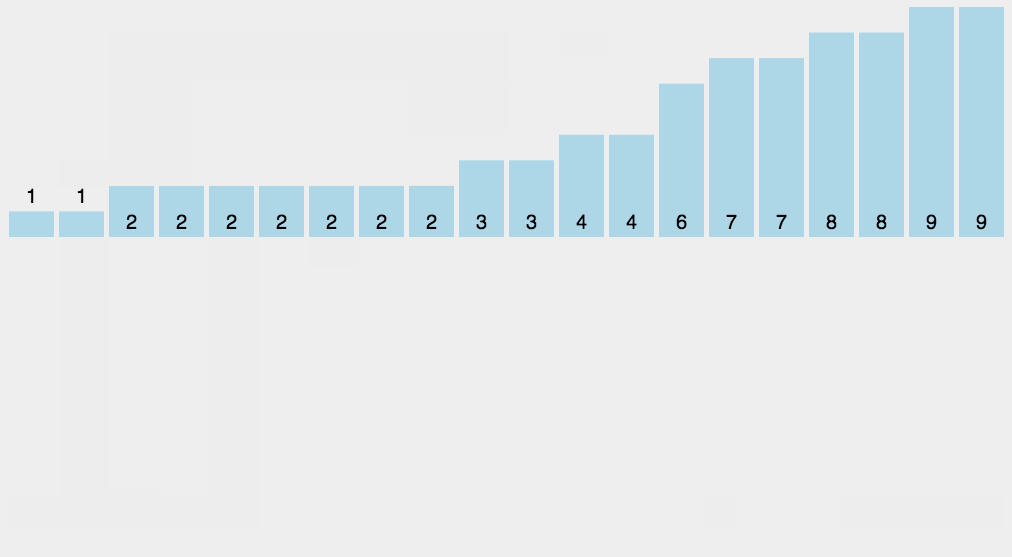
- 算法步骤:
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为
i的元素出现的次数,存入数组C的第i项; - 对所有的计数累加(从
C中的第一个元素开始,每一项和前一项相加); - 反向填充目标数组:将每个元素
i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
class Solution {
public:vector<int> sortArray(vector<int>& nums) {// CountSort 计数排序int n = nums.size();int minNum = INT_MAX, maxNum = INT_MIN;// 找到数组中的最小和最大元素 这里面最小的那个可能为负数for (int i = 0; i < n; ++i) {if (nums[i] < minNum) minNum = nums[i];if (nums[i] > maxNum) maxNum = nums[i];}// 构造计数数组vector<int> counts(maxNum - minNum + 1, 0);for (int i = 0; i < n; ++i) {++counts[nums[i] - minNum];}// 计数排序int index = 0;for (int i = 0; i < counts.size(); ++i) {while (counts[i] != 0) {nums[index++] = i + minNum;counts[i]--;}}return nums;}
};
桶排序

- 算法步骤:
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
class Solution
{
public:vector<int> sortArray(vector<int>& nums) {// BucketSort 桶排序int n = nums.size();// 获取数组的最小值和最大值int maxNum = nums[0], minNum = nums[0];for (int i = 1; i < n; ++i) {if (nums[i] > maxNum) maxNum = nums[i];if (nums[i] < minNum) minNum = nums[i];}// 初始化桶int bucketNum = 5, bucketSize = (maxNum - minNum) / bucketNum + 1;vector<vector<int>> buckets(bucketNum, vector<int>(0));// 小至大分桶for (int num : nums) {int bucketIndex = (num - minNum) / bucketSize;buckets[bucketIndex].emplace_back(num);}// 桶内排序for (int i = 0; i < buckets.size(); ++i) {sort(buckets[i].begin(), buckets[i].end());}// 从桶中依次取数int index = 0;for (auto& bucket : buckets) {for (int num : bucket) {nums[index++] = num;}}return nums;}
};
基数排序

- 算法步骤:
- 取得数组中的最大数,并取得位数;
arr为原始数组,从最低位开始取每个位组成radix数组;- 对
radix进行计数排序(利用计数排序适用于小范围数的特点);
class Solution {public:vector<int> sortArray(vector<int>& nums) {// RadixSort 基数排序int n = nums.size();// 预处理,让所有的数都大于等于0for (int i = 0; i < n; ++i) {nums[i] += 50000; // 50000为最小可能的数组大小}// 找出最大的数字,并获得其最大位数int maxNum = nums[0];for (int i = 0; i < n; ++i) {if (nums[i] > maxNum) maxNum = nums[i];}int num = maxNum, maxLen = 0;while (num) {++maxLen;num /= 10;}// 基数排序,低位优先int divisor = 1;for (int i = 0; i < maxLen; ++i) {radixSort(nums, divisor);divisor *= 10;}// 减去预处理量for (int i = 0; i < n; ++i) {nums[i] -= 50000;}return nums;}void radixSort(vector<int>& nums, int divisor)//divisor 目标位{vector<vector<int>> bucket(10, vector<int>(0, 0));//桶for (int i = 0; i < nums.size(); i++)//根据目标位的大小依次放入桶中{int number = nums[i] / divisor % 10;bucket[number].push_back(nums[i]);}for (int i = 0, index = 0; i < bucket.size(); i++)//从桶中取出并放入到nums中{for (int j = 0; j < bucket[i].size(); j++){nums[index++] = bucket[i][j];}}}
};
相关文章:

十大排序(C++版)
测试排序的题目: 912. 排序数组 - 力扣(LeetCode) 堕落的做法: class Solution { public:vector<int> sortArray(vector<int>& nums) {sort(nums.begin(),nums.end());return nums;} };视频推荐: …...
SpringMVC中的常用注解
Java知识点总结:想看的可以从这里进入 目录3.2、常用的注解3.2、常用的注解 Controller:代表此类是一个控制器,需要配置包的扫描。Spring MVC 是通过组件扫描机制查找应用中的控制器类的 在Spring6.0之后要求控制层必须添加该注解才会被识别成…...
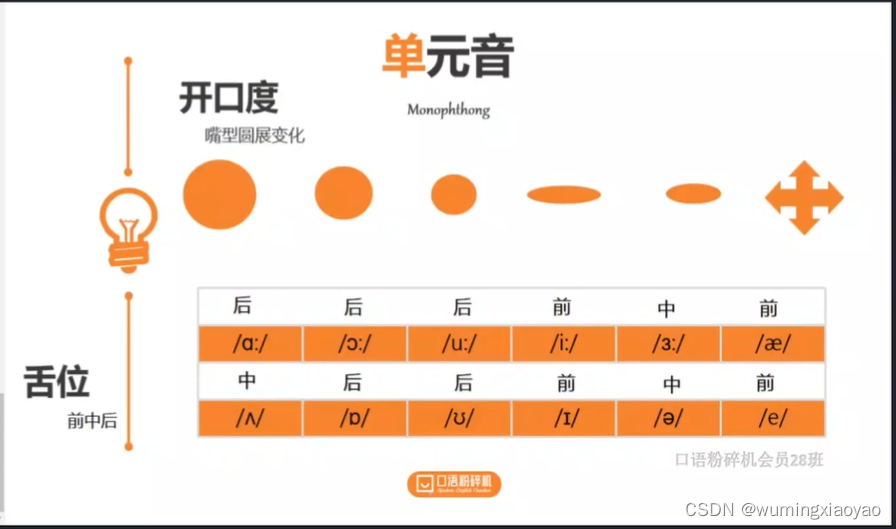
English Learning - L2-3 英音地道语音语调 小元音 [ʌ] [ɒ] [ʊ] [ɪ] [ə] [e] 2023.02.27 周一
English Learning - L2-3 英音地道语音语调 小元音 [ʌ] [ɒ] [ʊ] [ɪ] [ə] [e] 2023.02.27 周一课前活动练习方法大小元音总结小元音准备工作[ʌ] 中元音发音技巧对应单词的发音对应句子的发音常见的字母组合[ɒ] 后元音发音技巧对应单词的发音对应句子的发音常见的字母组合…...
fastadmin后台登录页修改
直接替换就行 <!DOCTYPE html> <html lang"{$config.language}"> <head>{include file"common/meta" /}<style type"text/css">body {color: #999;background-color: #f1f4fd;background-size: cover;}a {color: #444;…...
的三大特性)
Java 面向对象(OOP)的三大特性
封装 所谓封装,意思就是隐藏内部细节,在编程中,指利用抽象数据类型将数据和基于数据的操作封装在一起,使其构成一个不可分割的独立实体,并尽可能地隐藏内部的细节,只保留一些对外接口使之与外部发生联系。…...

Java:openjdk: error: Student is abstract; cannot be instantiated;java编译环境
文章目录编译环境jdkopenjdk错误代码小心javac -verbos编译环境 jdk 需要安装的javac 在java-devel 包里 [root10 ~]# rpm -qf /usr/bin/javac file /usr/bin/javac is not owned by any package [root10 ~]# ll /usr/bin/javac lrwxrwxrwx. 1 root root 23 Jun 15 09:52 /us…...

28个案例问题分析---019---临时解决方案和最终解决方案--思想
临时解决方案与最终解决方案一:背景介绍二:临时解决方案?最终解决方案?概念如何选择三:总结一:背景介绍 项目中,出现了一个线上问题。 用户登陆之后看不到课程。重新登陆就可以看到课程。出现这…...

计算机网络的166个概念你知道几个 第四部分
HTML:HTML 称为超文本标记语言,是一种标识性的语言。它包括一系列标签.通过这些标签可以将网络上的文档格式统一,使分散的 Internet 资源连接为一个逻辑整体。HTML 文本是由 HTML 命令组成的描述性文本,HTML 命令可以说…...

Lenovo 联想-IdeaPad-Y530电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板联想-IdeaPad-Y530处理器Intel 酷睿2双核 T9400已驱动内存2GB已驱动硬盘2TB HP EX950 PCI-E Gen3 x4 NVMe SSD已驱动显卡NVIDIA GeForce 9300M GS无法驱动声卡Realtek ALC888无法驱动网卡RTL8168H Giga…...
mac M1 nvm安装教程,避坑
mac M1 nvm 安装问题 新款的mac搭载了苹果自研的芯片,放弃了intel的x86芯片,那之前的软件难免会存在兼容性问题。 鄙人有幸踩了第一个坑。 在通过nvm 安装不同版本的node 时,出现了问题。 问题一:先说一下 nvm的安装问题&#…...

【项目精选】基于网络爬虫技术的网络新闻分析(视频+论文+源码)
点击下载源码 基于网络爬虫技术的网络新闻分析主要用于网络数据爬取。本系统结构如下: (1)网络爬虫模块。 (2)中文分词模块。 (3)中3文相似度判定模块。 (4)数据结构化存…...
【Python - Matplotlib】P2 plot 折线图
Matplotlib绘制折线图折线图完整代码与效果基础折线图设定横纵坐标设置中文显示添加网格添加描述信息再添加一个城市设置两个折线图前言 上一节内容主要围绕介绍 Matplotlib 的画板结构。 链接:https://blog.csdn.net/weixin_43098506/article/details/129331576 本…...
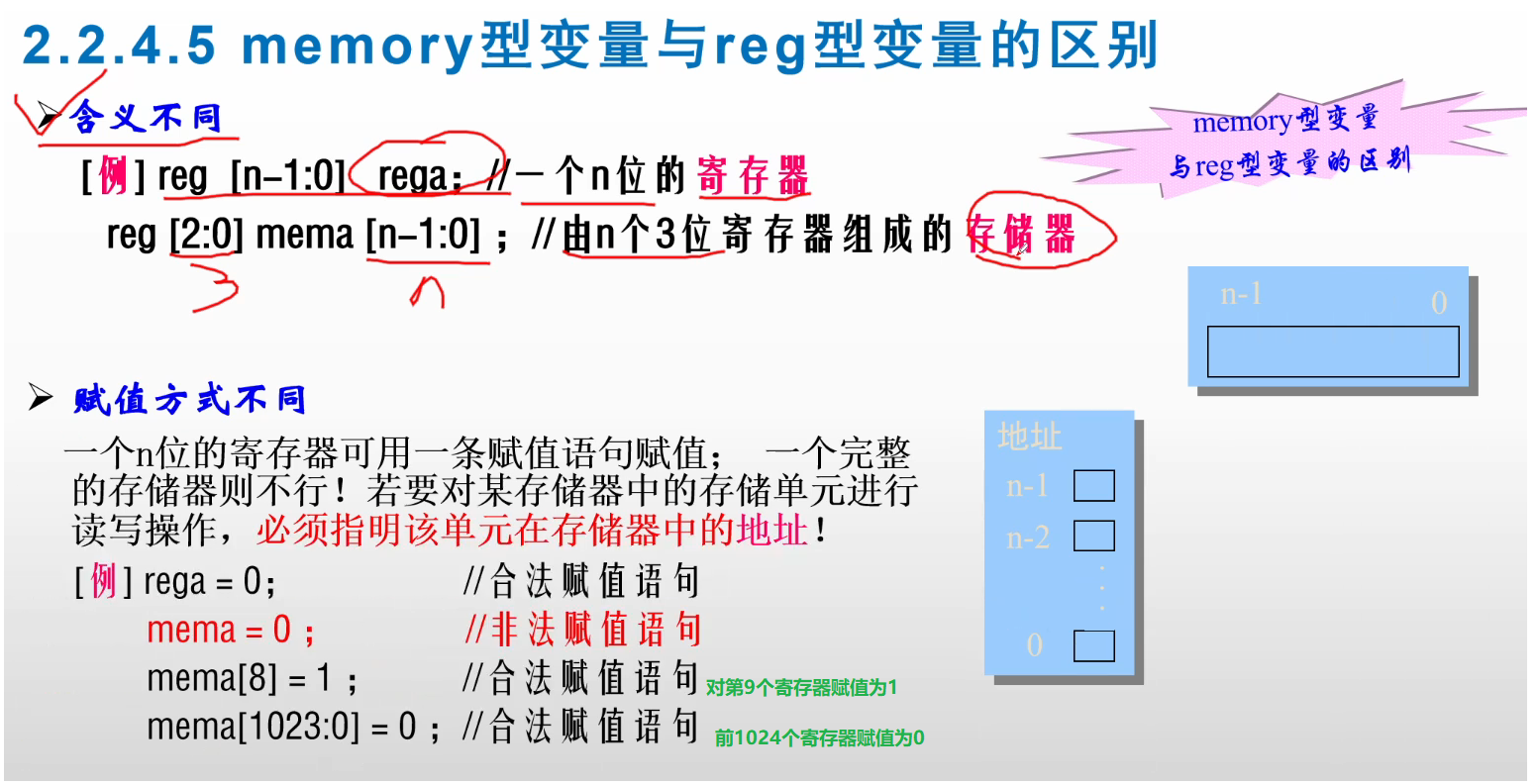
【Verilog】——模块,常量,变量
目录 1.模块 1.描述电路的逻辑功能 2. 门级描述 3.模块的模板编辑 2.关键字 3.标识符 4.Verilog源代码的编写标准 5.数据类型 1.整数常量 2.参数传递的两种方法 3.变量 4.reg和wire的区别 5.沿触发和电平触发的区别 6.memory型变脸和reg型变量的区别 1.模块 1.描…...

论文投稿指南——中文核心期刊推荐(电影、电视艺术)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...

Pip install 和Conda install 总结
版本一 conda install xxx:这种方式安装的库都会放在/Users/orion-orion/miniforge3/pkgs目录下。我们在我们的虚拟环境中要用到或下载时先到该路径下去找,若有则直接将其复制到我们的虚拟环境中包得存放位置: ~/site-packages/。若没有,则先…...
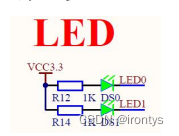
嵌入式系统实验——【玄武F103开发板】实现两个LED小灯闪烁
目录一、实验文件main.cstm32f10x.h二、实验思路(一)打开两个LED小灯1.在玄武F103开发板上找到LED0、LED1对应的GPIO控制寄存器2.找到GPIOB、GPIOE的地址3.打开APB2外设时钟的使能寄存器4.对GPIO寄存器进行设置对端口输出寄存器进行设置(二&a…...
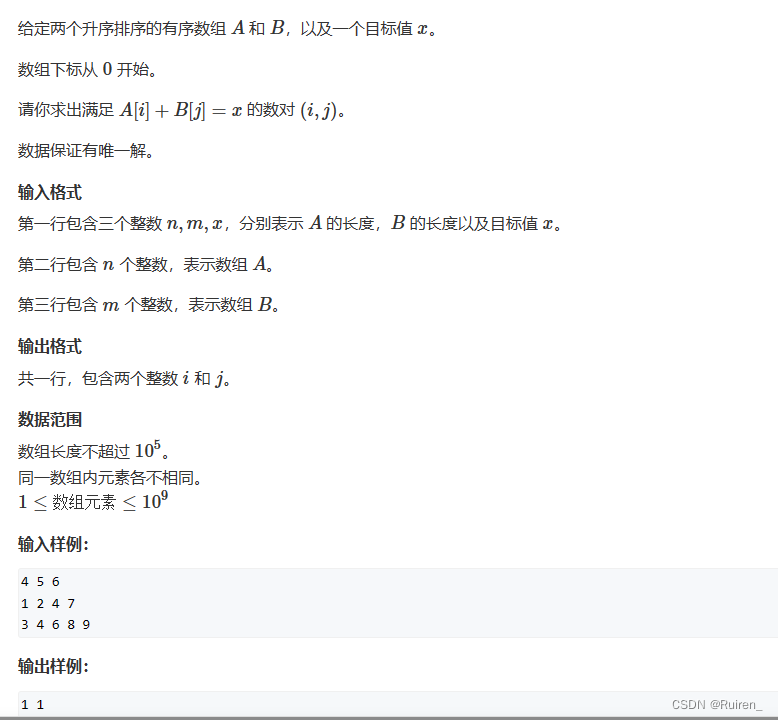
数组之双指针题
文章目录一、最长连续不重复子序列1.题目介绍2.思路3.二、长度最小的子数组1.题目介绍2.思路3.代码三、数组元素的目标和1.题目介绍2.思路3.代码总结其实在之前我写过不少双指针得题解,刷题专练之数组移除元素 刷题专练之翻转题练习这两篇文章的题解基本就是双指针法…...

真实需求和梦想实现满足
多少的时光和岁月中都不曾认真系统的深度思考自己的真实需求和欲望之间是否一致,随着时间的流逝才发现自己追求的是一场空,自己的真实需求并不是苦苦追求的东西,这也是当梦想照进现实!欲望是无善无恶的,不必为了满足自…...
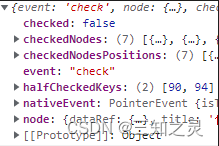
[ant-design-vue] tree 组件功能使用
[ant-design-vue] tree 组件功能使用描述环境信息相关代码参数说明描述 是希望展现一个树形的菜单,并且对应的菜单前有复选框功能,但是对比官网的例子,我们在使用的过程中涉及到对半选中情况的处理: 半选中状态: 选中…...

QT父子窗口事件传递与事件过滤器
处理监控系统的时候遇到问题,在MainWidget中创建多个子Widget的时候,原意是想鼠标点击先让MainWidget截获处理后再分派给子Widget去处理,但调试后发现如果子Widget重新实现了事件方法,就直接处理掉事件了,没有进到Main…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
