坚持刷题 | 平衡二叉树
文章目录
- 题目
- 考察点
- 代码实现
- 实现总结
- 对实现进一步改进
- 扩展提问
坚持刷题,老年痴呆追不上我,今天继续二叉树:平衡二叉树
题目
110.平衡二叉树
考察点
- 递归能力: 能否使用递归来解决问题。
- 树的基本操作:能否正确地访问节点的值,左子树,右子树等。
- 理解平衡二叉树:能够理解平衡二叉树的定义。
- 边界条件处理: 能否正确处理空树的情况。
- 时间和空间复杂度: 解决问题的方法是否具有合理的时间和空间复杂度。
代码实现
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class BinaryTreeBalance {public boolean isBalanced(TreeNode root) {if (root == null) {return true;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);// 检查当前节点是否平衡,并递归检查左右子树return Math.abs(leftHeight - rightHeight) <= 1&& isBalanced(root.left)&& isBalanced(root.right);}private int getHeight(TreeNode node) {if (node == null) {return 0;}// 递归计算左右子树的高度,取最大值加上当前节点的高度(1)return 1 + Math.max(getHeight(node.left), getHeight(node.right));}public static void main(String[] args) {BinaryTreeBalance solution = new BinaryTreeBalance();// 在这里构建你的二叉树TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);// 调用isBalanced方法判断是否为平衡二叉树boolean result = solution.isBalanced(root);// 输出结果System.out.println("Is the binary tree balanced? " + result);}
}
实现总结
- 递归:使用递归来计算每个节点的高度,参考 坚持刷题|二叉树的最大深度,检查左右子树的高度差是否超过1,若超过1,则说明不是平衡二叉树
- 时间复杂度: O(n log n)。因为对于每个节点,都需要计算其左右子树的高度,而计算高度的时间复杂度是 O(log n)
- 空间复杂度: O(log n),递归调用栈的深度等于该节点的高度。在平衡二叉树的情况下,树的高度是 O(log n) 级别的。因此,递归调用的空间复杂度是 O(log n)。需要注意的是,这里的空间复杂度并不仅仅是由递归调用所使用的空间构成,还包括了递归过程中的临时变量、参数传递等所占用的空间。
对实现进一步改进
避免重复计算节点的高度: 在上面的实现中,对每个节点都调用了getHeight方法来计算高度。这可能导致重复计算,尤其是对于同一个节点。为了避免这种情况,可以修改算法,使得在计算高度的同时判断平衡条件。
一边计算高度一边判断平衡条件: 可以在递归调用的过程中,一边计算左右子树的高度,一边判断当前节点是否满足平衡条件。这样可以避免递归两次计算相同节点的高度。
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class BalancedBinaryTree {public boolean isBalanced(TreeNode root) {return checkHeightAndBalance(root) != -1;}private int checkHeightAndBalance(TreeNode node) {if (node == null) {return 0; // 空树是平衡的,高度为0}int leftHeight = checkHeightAndBalance(node.left);if (leftHeight == -1) {return -1; // 左子树不平衡,直接返回-1}int rightHeight = checkHeightAndBalance(node.right);if (rightHeight == -1) {return -1; // 右子树不平衡,直接返回-1}// 判断当前节点是否平衡,如果不平衡则返回-1,否则返回当前节点的高度if (Math.abs(leftHeight - rightHeight) > 1) {return -1;} else {return Math.max(leftHeight, rightHeight) + 1; // 返回当前节点的高度}}public static void main(String[] args) {BalancedBinaryTree solution = new BalancedBinaryTree();// 在这里构建你的二叉树TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);// 调用isBalanced方法判断是否为平衡二叉树boolean result = solution.isBalanced(root);// 输出结果System.out.println("Is the binary tree balanced? " + result);}
}
在这个改进的实现中,checkHeightAndBalance方法返回-1表示不平衡,否则返回当前节点的高度。这样可以在计算高度的同时判断平衡条件,避免了重复计算。
扩展提问
可以用非递归的方式实现吗?时间复杂度和空间复杂度又会如何呢?
相关文章:

坚持刷题 | 平衡二叉树
文章目录 题目考察点代码实现实现总结对实现进一步改进扩展提问 坚持刷题,老年痴呆追不上我,今天继续二叉树:平衡二叉树 题目 110.平衡二叉树 考察点 递归能力: 能否使用递归来解决问题。树的基本操作:能否正确地访…...
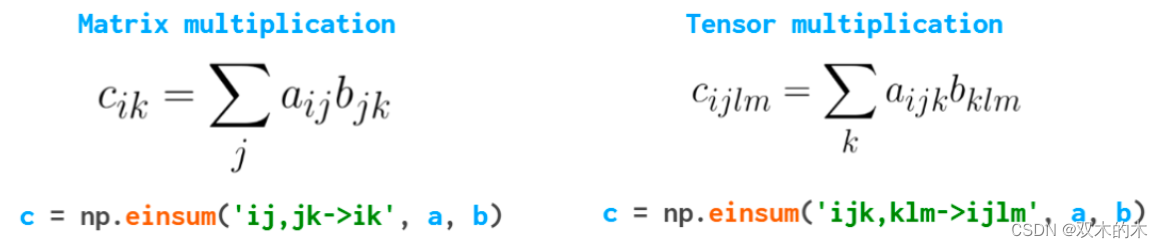
江大白 | 万字长文图解Numpy教程,看这一篇就够了!
本文来源公众号“江大白”,仅用于学术分享,侵权删,干货满满,有超级详细的图解。 原文链接:万字长文图解Numpy教程,看这一篇就够了! (qq.com) 以下文章来源于博客:Medium 作者&…...

数据结构——静态链表
1.定义: (1)单链表:各个结点散落在内存中的各个角落,每个结点有指向下一个节点的指针(下一个结点在内存 中的地址); (2)静态链表:用数组的方式来描述线性表的链式存储结构: 分配一…...

C++ 知识列表【图】
举例C的设计模式和智能指针 当谈到 C 的设计模式时,以下是一些常见的设计模式: 工厂模式(Factory Pattern):用于创建对象的模式,隐藏了对象的具体实现细节,只暴露一个公共接口来创建对象。 单例…...

系统登录的时候的密码如何做到以加密的形式进行登录【java.security包下的api】工具类。
/** description: 将普通的publicKey转化得到一个RSAPublicKey* author: zkw* date: 2024/1/24 16:17* param: publicKey 普通的publicKey* return: RSAPublicKey 得到一个新的RSAPublicKey**/public static RSAPublicKey getPublicKey(String publicKey) throws NoSuchAlgorit…...
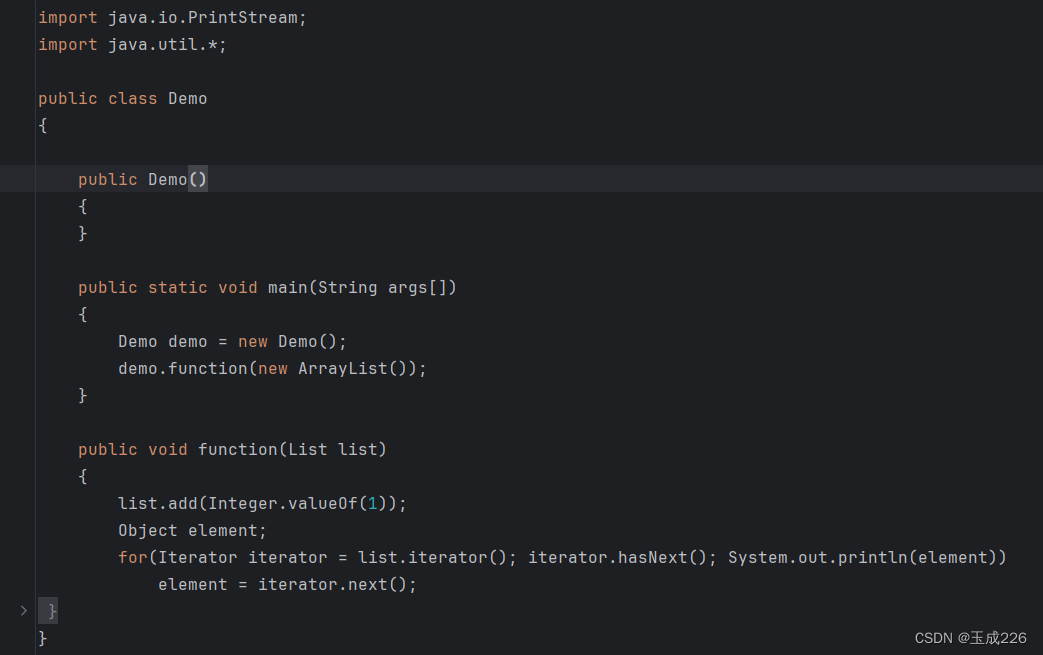
java基础学习: 什么是泛型的类型擦除
文章目录 一、什么是泛型2、泛型编译前和编译后对比3、泛型的优点(1)提高了代码的复用性和可读性(2)提高了代码的安全性 二、泛型的定义1、泛型类2、泛型接口3、泛型方法 三、泛型通配符1、?和T有什么区别2、通配符的分…...

Vue+OpenLayers7入门到实战:在地图上添加缩放控件、比例尺控件和鼠标经纬度位置显示控件
返回《Vue+OpenLayers7》专栏目录:Vue+OpenLayers7 前言 本章主要介绍如何使用OpenLayers7在地图上添加地图缩放控件,比例尺显示控件和鼠标经纬度位置展示控件这三个Control控件。 二、依赖和使用 "ol": "7.5.2"使用npm安装依赖npm install ol@7.5.…...

极简生活|可以慢慢变富的8个习惯
哈喽,大家好啊,我是雷工! 巴菲特巴老爷子曾经多次指出: 大多数投资者的问题就在于不愿意慢慢变富。 可是大多数人都急于一夜暴富,于是乎那么多的追涨杀跌,不断上演,越急功近利反而越损失惨重。 …...

MySQL基础(一)
学习数据库的目的: 实现数据持久化到本地。使用完整的管理系统统一管理,可以实现结构化查询,方便管理。 一、数据库概述 数据库(DataBase) 为了方便数据的存储和管理,它将数据按照特定的 规则存储在磁盘…...

【Linux编译器-gcc/g++使用】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 设计样例,先见一下 方案一: 方案二: 在企业里面一般维护软件的源代码的话,要维护几份? 方案一&…...

SQL提示与索引终章
✨博客主页:小小恶斯法克的博客 🎈该系列文章专栏:重拾MySQL-进阶篇 📜 感谢大家的关注! ❤️ 可以关注黑马IT,进行学习 目录 🚀SQL提示 🚀覆盖索引 🚀前缀索引 &…...
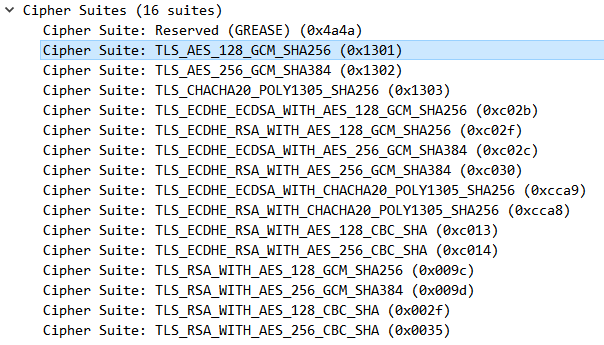
基于OpenSSL的SSL/TLS加密套件全解析
概述 SSL/TLS握手时,客户端与服务端协商加密套件是很重要的一个步骤,协商出加密套件后才能继续完成后续的握手和加密通信。而现在SSL/TLS协议通信的实现,基本都是通过OpenSSL开源库,本文章就主要介绍下加密套件的含义以及如何在O…...
01-echarts如何绘制三维折线图
echarts如何绘制三维折线图 一、相关依赖包1、下载依赖2、引入依赖 二、创建图表盒子1、创建盒子2、定义数据3、编写方法1、初始化盒子2、设置配置项3、修改数据格式4、设置颜色数组4、设置name数组5、设置线三维和点三维6、添加配置项7、设置图表自适应 4、调用方法 三、整体代…...

Linux-共享内存
文章目录 前言一、system V共享内存申请共享内存挂载共享内存删除共享内存挂载删除共享内存 二、示例代码三.运行效果 前言 在这之前我们已经学习了两种进程间通信方式:匿名管道和命名管道。 从我们之前的学习已经知道,想让多个进程间进行通信就需要让他…...

深入分析 Linux 网络丢包问题
热门IT课程【视频教程】-华为/思科/红帽/oraclehttps://xmws-it.blog.csdn.net/article/details/134398330 所谓丢包,是指在网络数据的收发过程中,由于种种原因,数据包还没传输到应用程序中,就被丢弃了。这些被丢弃包的数量&#…...
web安全学习笔记【08】——算法1
思维导图在最后 #知识点: 1、Web常规-系统&中间件&数据库&源码等 2、Web其他-前后端&软件&Docker&分配站等 3、Web拓展-CDN&WAF&OSS&反向&负载均衡等 ----------------------------------- 1、APP架构-封装&原生态&…...
2024最新版Python 3.12.1安装使用指南
2024最新版Python 3.12.1安装使用指南 Installation and Configuration Guide to the latest version Python 3.12.1 in 2024 By Jackson Python编程语言,已经成为全球最受欢迎的编程语言之一;它简单易学易用,以标准库和功能强大且广泛外挂…...
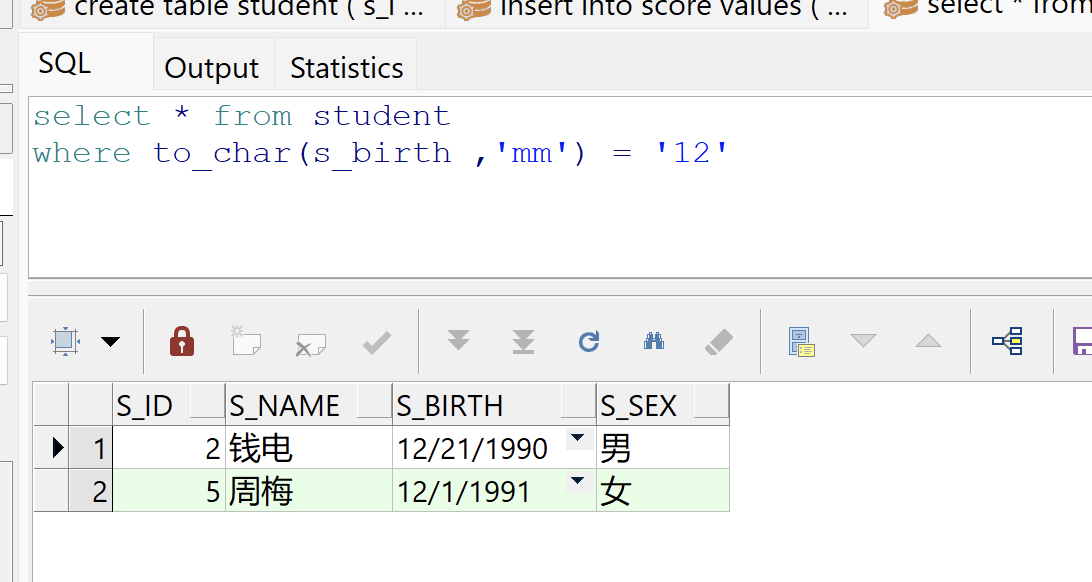
Oracle 经典练习题 50 题
文章目录 一 CreateTable二 练习题1 查询"01"课程比"02"课程成绩高的学生的信息及课程分数2 查询"01"课程比"02"课程成绩低的学生的信息及课程分数3 查询平均成绩大于等于60分的同学的学生编号和学生姓名和平均成绩4 查询平均成绩小于…...

PyTorch的衍生资源
PyTorch作为深度学习领域的一个重要框架,自2016年首次发布以来经历了显著的发展。以下是PyTorch发展过程中的几个关键里程碑事件: 2016年: PyTorch于2016年首次发布,作为一个基于动态计算图的开源机器学习库,它提供了自…...

开源项目Git Commit规范与ChangeLog
一,conventional commit(约定式提交) Conventional Commits 是一种用于给提交信息增加人机可读含义的规范。它提供了一组用于创建清晰的提交历史的简单规则。 1.1 作用 自动化生成 CHANGELOG基于提交类型,自动决定语义化的版本变更向项目相关合作开发…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
