二叉树的最大深度[简单]

优质博文:IT-BLOG-CN
一、题目
给定一个二叉树root,返回其最大深度。
二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
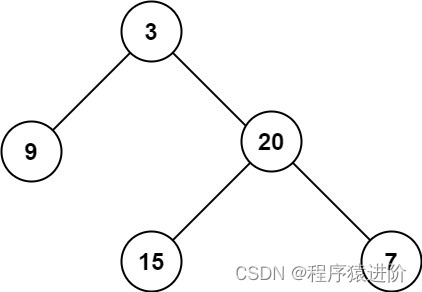
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
树中节点的数量在
[0, 104]区间内。
-100 <= Node.val <= 100
二、代码
【1】深度优先搜索: 如果我们知道了左子树和右子树的最大深度l和r,那么该二叉树的最大深度即为max(l,r)+1。而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言,在计算当前二叉树的最大深度时,可以先递归计算出其左子树和右子树的最大深度,然后在O(1)时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {// 递归计算数的深度,确定递归的推出条件if (root == null) {return 0;} else {int leftHight = maxDepth(root.left);int rightHight = maxDepth(root.right);return Math.max(leftHight,rightHight) + 1;}}
}
复杂度分析:
1、时间复杂度: O(n)其中n为二叉树节点的个数。每个节点在递归中只被遍历一次。
2、空间复杂度: O(height)其中height表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
【2】广度优先搜索: 我们也可以用「广度优先搜索」的方法来解决这道题目,但我们需要对其进行一些修改,此时我们广度优先搜索的队列里存放的是当前层的所有节点。每次拓展下一层的时候,不同于广度优先搜索的每次只从队列里拿出一个节点,我们需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即我们是一层一层地进行拓展,最后我们用一个变量ans来维护拓展的次数,该二叉树的最大深度即为ans。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<TreeNode>();// 先存放root节点queue.offer(root);// 总长度int maxLen = 0;// 开启循环,并确定退出循环的条件while (!queue.isEmpty()) {// 获取当前队列的长度,确定该层遍历的次数int size = queue.size();// 我们需要遍历当前层的所有 treeNode// 确定循环条件,并确定退出条件while (size > 0) {TreeNode treeNode = queue.poll();if (treeNode.left != null) {// 注意:添加的时左节点,而不是当前节点queue.offer(treeNode.left);}if (treeNode.right != null) {queue.offer(treeNode.right);}--size;}++maxLen;}return maxLen;}
}
复杂度分析:
1、时间复杂度: O(n)其中n为二叉树的节点个数。与方法一同样的分析,每个节点只会被访问一次。
2、空间复杂度: 此方法空间的消耗取决于队列存储的元素数量,其在最坏情况下会达到O(n)。
相关文章:

二叉树的最大深度[简单]
优质博文:IT-BLOG-CN 一、题目 给定一个二叉树root,返回其最大深度。 二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 示例 2:…...

[Redis]不同系统间安装redis服务器
日常服务器端开发,消息队列等需求,免不了用到redis,搭建一个redis服务器,方便开发和测试,我们从以下三类系统来说明下: 安装 Redis 服务器的过程因操作系统而异。以下是在常见的 Linux 发行版(…...
Unity之动画和角色控制
目录 📕 一、动画 1.创建最简单的动画 2.动画控制器 📕二、把动画和角色控制相结合 📕三、实现实例 3.1 鼠标控制角色视角旋转 3.2 拖尾效果 📕四、混合动画 最近学到动画了,顺便把之前创建的地形࿰…...

C语言库函数实现字符串转大小写
目录 引言 代码 引言 处理字符串时,除了将字符串中的所有大写字母转换为小写字母外,我们还可以利用其他相关函数进行更丰富的文本操作。本文将以一段使用isupper()、tolower()函数实现字符串全转小写的C语言程序为例,详细介绍这两个函数以及…...
hcip----ospf
一:动态路由协议 IGP 协议---RIP OSPF ISIS EIGRP EGP--EGP ---BGP 三个角度的评判一款动态路由协议的优劣 RIP --request response 1.选路--选路依据不好,可能出现环路 2.收敛速度--计时器 3.占用资源-- RIPV1 RIPV2 RIPNG--ipv6 OSPFV1 OSPFV…...

vue中如何写过滤器
全局注册 (可以在main.js中进行全局注册 vue.fifler(test’,function(v){return v0? ‘终止’:v1?进行中:异常 })在组件页面使用 <view>{{state|test}}</view> <script> export default {data(){return {state: 1// state 1 进行中…...
)
c语言-文件的读写操作(下)
文章目录 前言一、文件的随机读写1.1 fseek()1.2 ftell()1.3 rewind() 总结 前言 本篇文章介绍c语言中文件的随机读写 一、文件的随机读写 1.1 fseek() fseek()函数的作用是根据文件指针的位置和偏移量定位文件指针 int fseek ( FILE * stream, long int offset, int origi…...

android学习笔记----SQLite数据库
用SQLite语句执行: 首先看到界面: 代码如下: MainActivity.java import android.support.v7.app.AppCompatActivity; import android.os.Bundle; import android.text.TextUtils; import android.view.View; import android.widget.EditTe…...

开发知识点-Flutter移动应用开发
支持 安卓 IOS Android 鸿蒙 第一章dart基础章节介绍 移动电商——Flutter-广告Banner组件制作 移动电商——Flutter实战课程介绍 Flutter实例——路由跳转的动画效果...

视频尺寸魔方:分层遮掩3D扩散模型在视频尺寸延展的应用
▐ 摘要 视频延展(Video Outpainting)是对视频的边界进行扩展的任务。与图像延展不同,视频延展需要考虑到填充区域的时序一致性,这使得问题更具挑战性。在本文中,我们介绍了一个新颖的基于扩散模型的视频尺寸延展方法——分层遮掩3D扩散模型(…...

openssl3.2/test/certs - 061 - other@good.org not permitted by CA1
文章目录 openssl3.2/test/certs - 061 - othergood.org not permitted by CA1概述笔记END openssl3.2/test/certs - 061 - othergood.org not permitted by CA1 概述 openssl3.2 - 官方demo学习 - test - certs 笔记 /*! * \file D:\my_dev\my_local_git_prj\study\openSS…...

如何实现无公网ip远程访问本地websocket服务端【内网穿透】
文章目录 1. Java 服务端demo环境2. 在pom文件引入第三包封装的netty框架maven坐标3. 创建服务端,以接口模式调用,方便外部调用4. 启动服务,出现以下信息表示启动成功,暴露端口默认99995. 创建隧道映射内网端口6. 查看状态->在线隧道,复制所创建隧道的公网地址加端口号7. 以…...

pip清华源怎么换回来
怎么临时使用清华源 pip install scrapy -i https://pypi.Python.org/simple/怎么永久换源 pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple修改清华源后怎么换回来 删掉/home/XXX/.config/pip/pip.conf...

[Go]认识Beego框架
对比Gin的简洁,自己之前基于Gin撸了一个架子,确实比beego目录看着舒服多了,不过最近接触到beego的项目,beego的bee工具使用还是很方便,来简单梳理下细节; Beego是一个开源的Go语言Web应用框架,…...
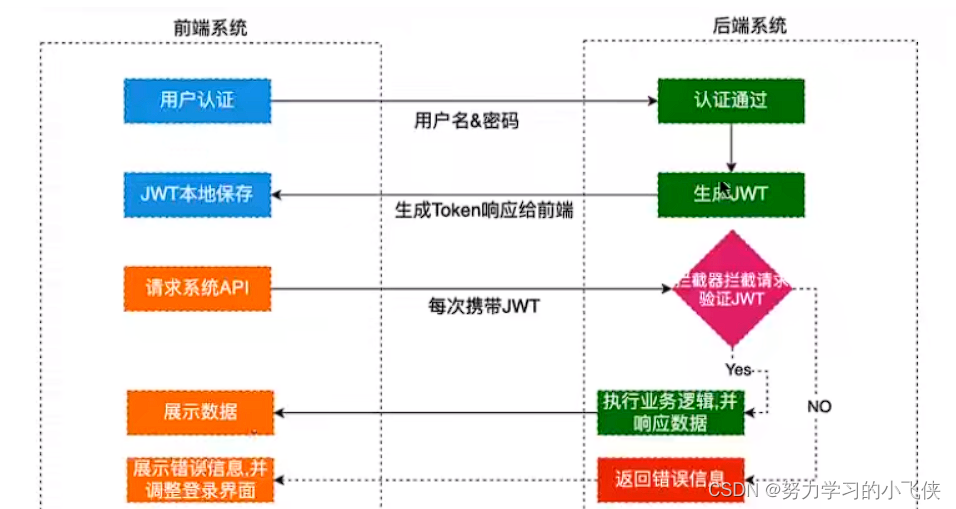
JWT登录
JWT JSON Web Token(JSON Web令牌) 是一个开放标准(rfc7519),它定义了一种紧凑的、自包含的方式,用于在各方之间以JSON对象安全地传输信息。此信息可以验证和信任,因为它是数字签名的。jwt可以使用秘密〈使用HNAC算法…...

MySQL和Redis的事务有什么异同?
MySQL和Redis是两种不同类型的数据库管理系统,它们在事务处理方面有一些重要的异同点。 MySQL事务: ACID属性: MySQL是一个关系型数据库管理系统(RDBMS),支持ACID属性,即原子性(Ato…...
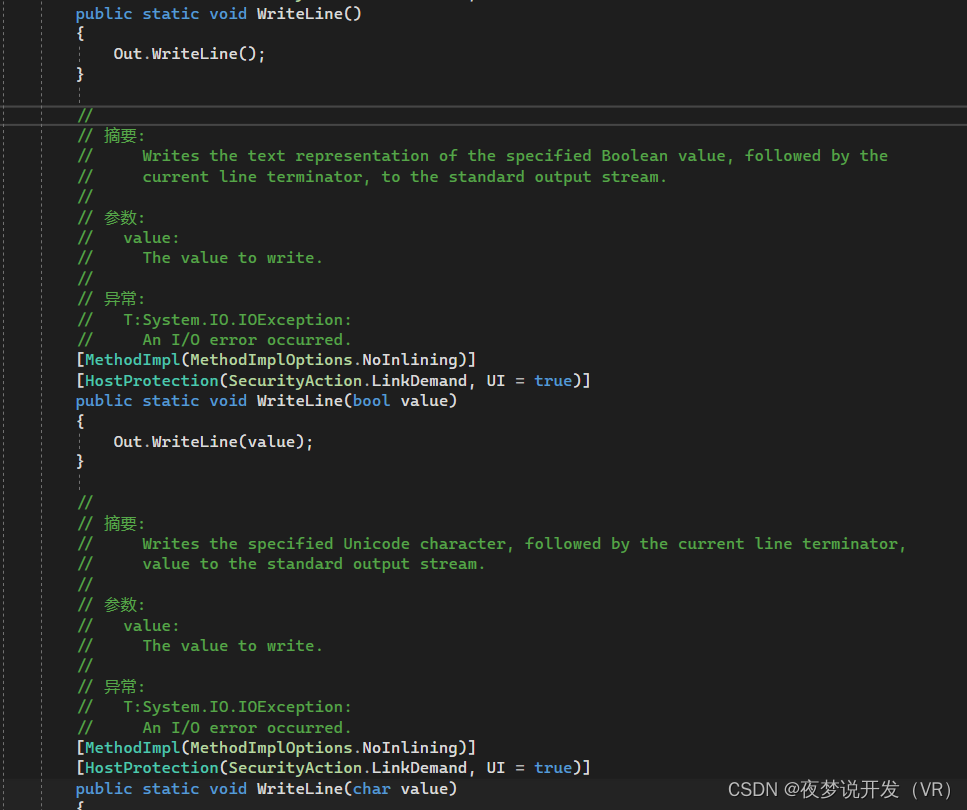
【C#】基础巩固
最近写代码的时候各种灵感勃发,有了灵感,就该实现了,可是,实现起来有些不流畅,总是有这样,那样的卡壳,总结下来发现了几个问题。 1、C#基础内容不是特别牢靠,理解的不到位ÿ…...
)
基于Skywalking开发分布式监控(一)
接手为微服务系统搞链路监控项目一年多,也和skywalking打了一年多的交道,也应该有个总结,主要谈一下搭建监控系统遇到的难点和解决方案。 说明: 本文的代码均由本地演示代码替代,非实际代码 为啥选skywalking…...

高防服务器什么意思
高防服务器什么意思,为什么要用高防服务器,小编为您整理发布高防服务器什么意思的解读。 高防服务器是指具备较高防御能力的服务器,能够抵御DDoS/CC等网络攻击。 高防服务器通常用于保护游戏、APP、金融、电商等业务,这些领域因为…...
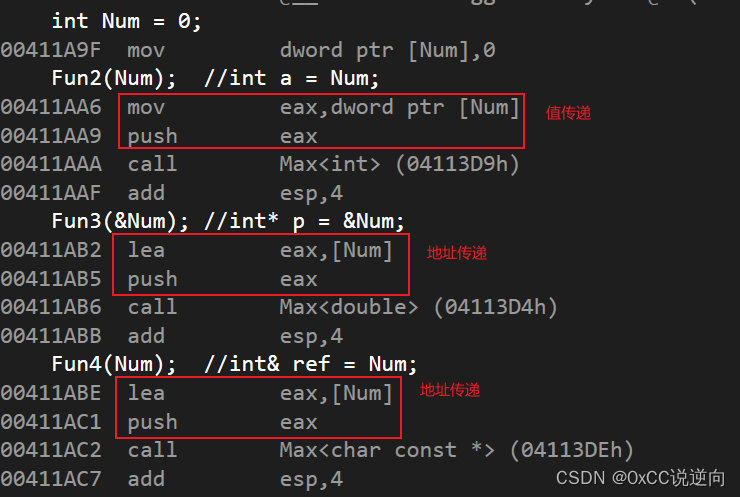
C/C++ - Auto Reference
目录 auto Reference auto 当使用auto关键字声明变量时,C编译器会根据变量的初始化表达式推断出变量的类型。 自动类型推断:auto关键字用于自动推断变量的类型,使得变量的类型可以根据初始化表达式进行推导。 初始化表达式&#x…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
