SLAM初学
昨天组长布置了任务,要求看香港大学的一篇论文,一打开,好家伙,纯英文,直接翻译着看
几个读不懂的概念:
体素:体素是三维空间中的体积像素的简称。它类似于二维图像中的像素,但在三维空间中表示立体体素单元。体素可以被看作是一个立方体,具有一定的体积、位置和属性。
三角形网络:计算机图形学中常用的表示三维对象表面的方法之一。它由许多相互连接的三角形组成,每个三角形由三个顶点和三条边组成,三角形网格是一种离散化的表示方法,通过将三维表面划分为许多小的三角形来近似实际的曲面或物体。这些三角形可以是规则的(等边三角形)或不规则的,具体取决于表面的形状和拓扑结构。

泊松曲面重建的方法 :是一种常用的曲面重建方法,用于从离散的点云数据中重建连续的曲面模型。它基于泊松方程的性质,通过求解离散点云的泊松方程来估计曲面的法线和位置信息。
(泊松方程,看了,不太懂,做这个,直接套公式能用就行)

泊松曲面重建方法具有一定的优势,它能够有效地重建光滑的曲面,并且对于噪声和不完整的点云数据也有一定的鲁棒性。然而,它也有一些限制,例如对于大规模点云数据的处理较慢,并且对于具有细节或复杂几何形状的曲面可能无法完全恢复。
所以可以在大雾天气或者沙尘暴等天气中应用泊松方程
三角测量:三角测量是一种将点集连接成三角形的方法,使得任意两个点之间的连线不会穿过其他的三角形。它基于一组点的相对位置关系来构建三角形网格。三角测量的结果是一个无重叠的三角形网格,其中每个三角形的外接圆不包含其他点
图切:图切是一种将空间分割为多个区域的方法,每个区域包含一个点,并且该点到区域内所有点的距离最近。图切图是由一组点的图切区域和图切边构成的。图切图可以用于计算几何、空间分析和图形处理等领域。对于给定的点集,图切图的边界由相邻点之间的垂直平分线组成。
TSDF方法: 基本思想是通过融合多个深度图像或点云观测来估计场景的几何形状。对于每个观测到的深度图像或点云,TSDF方法将其中的点投影到体素格子中,并根据点的深度信息更新对应体素格子的距离值。通过多次观测和融合,可以逐步构建出场景的三维几何表示。
TSDF方法的关键是对距离值进行融合和更新。常用的融合方式是加权平均,其中权重可以根据观测的可靠性进行设置。对于每个新观测到的点,需要将其投影到体素格子中,并更新相应格子的距离值。距离值的更新可以根据当前距离值和新观测点的深度值进行插值计算
我体会到TSDF方法就是将观察到得图像上的每个点都标记上距离,经过多次观察并融合就可以知道具体得环境信息。(不准,我自己得感受)
三角形片元:是三维图形学中的基本几何单元,由三个顶点组成的三角形形状。在渲染和图形处理中,三角形片元被广泛应用于三维模型的表示、光栅化、着色和绘制等方面。

三角形片元是它经过顶点着色器的处理后,被传递到几何着色器进行裁剪、投影和变换等操作。然后,经过光栅化阶段,三角形片元被转化为像素,并进行插值计算,最终被传递给片元着色器进行颜色计算和纹理采样等操作。
通过组合和连接多个三角形片元,可以构建出复杂的三维模型,并进行高质量的渲染和可视化。
双步管道:是一种图形渲染管线的组织方式,用于实现高级的图形效果和渲染技术。它由两个主要的渲染阶段组成,分别是几何处理阶段和像素处理阶段。

这种分离的设计使得渲染算法更加模块化和可扩展,同时也方便实现一些高级的渲染效果,如法线映射、阴影计算、抗锯齿等。
增量重建三角形网格:用于从离散的点云数据中逐步生成连续的三角形网格模型。这种方法通常用于三维重建、计算机视觉和计算机图形学等领域。
增量重建三角形网格的基本思想是通过逐步添加点和三角形来构建网格模型,而不是一次性处理所有的点云数据。这种方法的优势在于它可以有效地处理大规模的点云数据,并且能够动态地适应新加入的点。(可以实现实时性)
KD树:是一种用于高效处理k维空间数据的数据结构。它是一种二叉树,其中每个节点代表一个k维数据点,并根据数据点在每个维度上的值进行划分。KD树的构建过程和搜索算法使得它适用于范围查询、最近邻搜索和近似最近邻搜索等问题。
在KD树中,每个节点都有一个关联的k维数据点,并且根据某个维度上的值进行划分。例如,对于二维空间中的点,可以先选择x轴或y轴作为划分维度,然后根据该维度上的值将数据点划分为左子树和右子树。然后,对于每个子树,选择另一个维度作为划分维度,再次进行划分。这样递归地构建KD树,直到每个子树中只包含一个数据点或没有数据点为止。


相关文章:

SLAM初学
昨天组长布置了任务,要求看香港大学的一篇论文,一打开,好家伙,纯英文,直接翻译着看 几个读不懂的概念: 体素:体素是三维空间中的体积像素的简称。它类似于二维图像中的像素,但在三…...
腾讯云轻量应用服务器Docker如何一键搭建属于自己的幻兽帕鲁服务器?
幻兽帕鲁/Palworld是一款2024年Pocketpair开发的开放世界生存制作游戏,在帕鲁的世界,玩家可以选择与神奇的生物“帕鲁”一同享受悠闲的生活,也可以投身于与偷猎者进行生死搏斗的冒险。而帕鲁可以进行战斗、繁殖、协助玩家做农活,也…...
win10+elasticsearch8.12 安装教程
Elasticsearch是一种搜索引擎,本地安装完成之后,可使用其他编程语言(例如python)与elasticsearch建立连接,然后使用python脚本搜索elasticsearch中的数据 1下载 elasticsearch elasticsearch最新版官网下载链接 点击…...

经典面试题-死锁
目录 1.什么是死锁? 2.形成死锁的四个必要条件 3.死锁的三种情况 第一种情况: 举例: 举例: 第二种情况:两个线程 两把锁 举例: 第三种情况:N个线程 M把锁 哲学家进餐问题 1.什么是死锁&…...

mysql面试题合集-基础
前言 工作很忙,本质还是自己比较懒惰,很久没更新博客了。近期打算面试,换个工作环境,那就先从面试题开始吧,后续也会逐渐更新自己在工作中的一些经验感悟。接下来切入主题,由于长期做前台开发工作…...
)
点灯大师(STM32)
这段代码是用于STM32F10x系列微控制器的C语言程序,目的是初始化GPIOC的Pin 13为输出,并设置其输出高电平。以下是对代码的逐行解释: #include "stm32f10x.h" 这一行引入了STM32F10x设备的头文件,包含了用于STM32F10x系…...

@EnableEurekaServer
定义:EnableEurekaServer注解是Spring Cloud中的一个注解,用于将Spring Boot应用程序指定为Eureka服务器。 Eureka服务器是一个服务注册中心,也被称为发现服务器,管理和协调微服务。保存有关所有客户端服务应用程序的信息。 每个…...

Java中的接口
六. 接口 特性1 - 解决单继承 语法如下 interface A {public default void a() {} }interface B {public default void b() {} }// C 从 A, B 两个接口重用方法 a() 和 b() class C implements A, B {}解决之前的问题 public class TestInterface1 {public static void mai…...

Linux笔记之bash脚本中的-e、和
Linux笔记之bash脚本中的-e、&和&& code review! 文章目录 Linux笔记之bash脚本中的-e、&和&&1.&和&&2.-e 1.&和&& 在Linux bash脚本中,&符号有几个不同的用途,这里列举了一些常见的情况…...

mapstruct自定义转换,怎样将String转化为List
源码:https://gitee.com/cao_wen_bin/test 最近在公司遇到了这样一个为题,前端传过来的是一个List<Manager>,往数据库中保存到时候是String,这个String使用谷歌的json转化器。 当查询的时候在将这个数据库中String的数据以List<Mana…...

torch.matmul和torch.bmm区别
torch.matmul可用于4维数组的相乘,而torch.bmm只能用户3维数组的相乘,以/home/tiger/.local/lib/python3.9/site-packages/transformers/models/vit/modeling_vit.py中的ViTSelfAttention实现为例,在transpose_for_scores之前的shape是(batch…...

k8s学习(RKE+k8s+rancher2.x)成长系列之概念介绍(一)
一、前言 本文使用国内大多数中小型企业使用的RKE搭建K8s并拉起高可用Rancher2.x的搭建方式,以相关技术概念为起点,实际环境搭建,程序部署为终点,从0到1的实操演示的学习方式,一步一步,保姆级的方式学习k8…...

PHP - Yii2 异步队列
1. 前言使用场景 在 PHP Yii2 中,队列是一种特殊的数据结构,用于处理和管理后台任务。队列允许我们将耗时的任务(如发送电子邮件、push通知等)放入队列中,然后在后台异步执行。这样可以避免在处理大量请求时阻塞主应用…...

leetcode560和为k的子数组
class Solution { public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int>mp;mp[0]1;int count0,pre0;for(auto& x:nums){prex;if(mp.find(pre-k)!mp.end()){countmp[pre-k];}mp[pre];}return count;} }; 一个超级好的思路࿰…...
【ProtoBuf】使用指南
一.什么是ProtoBuf 特点:ProtoBuf是用于序列化和反序列化的一种方法,类似xml和json,但是效率更高,体积更小。ProtoBuf具有语⾔⽆关、平台⽆关,扩展性、兼容性好等特点。 ProtoBuf是需要依赖通过编译生成的头文件和源…...

Buffer Pool
Buffer Pool 概念free链表flush链表LRU链表chunk 概念 MySQL在启动时向操作系统申请的一片连续的内存,默认128M。然后将这块内存分为一个一个缓冲页(16KB,因为页就是16KB的)。再为每个缓冲页创建对应的控制块用于管理。比如第一次查询数据之后ÿ…...

jetson-inference----docker内运行分类任务
系列文章目录 jetson-inference入门 jetson-inference----docker内运行分类任务 文章目录 系列文章目录前言一、进入jetson-inference的docker二、分类任务总结 前言 继jetson-inference入门 一、进入jetson-inference的docker 官方运行命令 进入jetson-inference的docker d…...

Python脚本之操作Redis Cluster【二】
本文为博主原创,未经授权,严禁转载及使用。 本文链接:https://blog.csdn.net/zyooooxie/article/details/112484045 之前写过一篇 使用redis-py来操作redis集群, https://blog.csdn.net/zyooooxie/article/details/123760358 &am…...

认识数学建模
文章目录 1 什么是数学建模2 数学建模的比赛形式3 参加数学建模的好处4 数学建模的流程5 数学建模成员分工6 数学建模常用软件7 数学建模竞赛7.1 美国大学生数学建模竞赛7.2 MathorCup高校数学建模挑战赛7.3 华中杯大学生数学建模挑战赛7.4 认证杯数学建模网络挑战赛7.5 华东杯…...
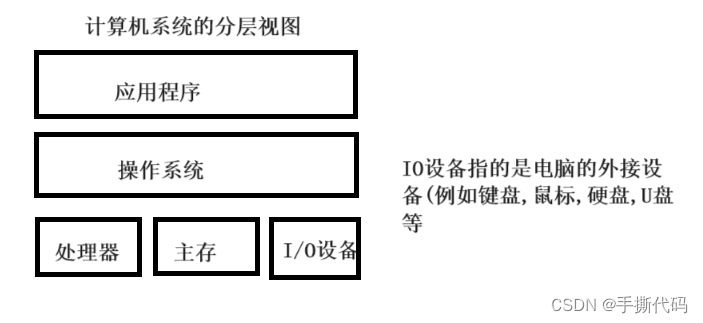
计算机工作原理解析和解剖(基础版)
我们会从软件⼯程师的⻆度解释计算机是如何⼯作的,我们的主要⽬标既不是期待 ⼤家可以造出⾃⼰的计算机,也不是介绍如何编程,⽽是希望让⼤家了解计算机的核⼼⼯作机制后,打破计算机的神秘感,并且有利于理解我们平时编程…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
