leetcode1237. 找出给定方程的正整数解
1237. 找出给定方程的正整数解![]() https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/
https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/
难度中等 101
给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)
函数接口定义如下:
interface CustomFunction {
public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y);
};
你的解决方案将按如下规则进行评判:
- 判题程序有一个由
CustomFunction的9种实现组成的列表,以及一种为特定的z生成所有有效数对的答案的方法。 - 判题程序接受两个输入:
function_id(决定使用哪种实现测试你的代码)以及目标结果z。 - 判题程序将会调用你实现的
findSolution并将你的结果与答案进行比较。 - 如果你的结果与答案相符,那么解决方案将被视作正确答案,即
Accepted。
示例 1:
输入:function_id = 1, z = 5 输出:[[1,4],[2,3],[3,2],[4,1]] 解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y 以下 x 和 y 满足 f(x, y) 等于 5: x=1, y=4 -> f(1, 4) = 1 + 4 = 5 x=2, y=3 -> f(2, 3) = 2 + 3 = 5 x=3, y=2 -> f(3, 2) = 3 + 2 = 5 x=4, y=1 -> f(4, 1) = 4 + 1 = 5
示例 2:
输入:function_id = 2, z = 5 输出:[[1,5],[5,1]] 解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y 以下 x 和 y 满足 f(x, y) 等于 5: x=1, y=5 -> f(1, 5) = 1 * 5 = 5 x=5, y=1 -> f(5, 1) = 5 * 1 = 5
提示:
1 <= function_id <= 91 <= z <= 100- 题目保证
f(x, y) == z的解处于1 <= x, y <= 1000的范围内。 - 在
1 <= x, y <= 1000的前提下,题目保证f(x, y)是一个 32 位有符号整数。
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* public:* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* int f(int x, int y);* };*/class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {}
};遍历法:
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;for (int x = 1; x <= 1000; x++) {for (int y = 1; y <= 1000; y++) {if (customfunction.f(x, y) == z) {res.push_back({x, y});}}}return res;}
};这段代码是一个解决问题的解法,它通过遍历x和y的取值范围从1到1000,并调用`customfunction.f(x, y)`方法进行计算,判断计算结果是否等于目标值z。如果相等,将当前的x和y加入到结果集res中。
整个算法的时间复杂度为O(n^2),其中n为1000。因为有两个嵌套的循环,每个循环都需要执行1000次,所以总共需要执行1000 * 1000 = 1000000次。
这个解法适用于求解自定义函数的问题,通过遍历所有可能的参数组合来查找满足特定条件的解。在这个例子中,我们通过遍历x和y的取值范围来寻找使得customfunction.f(x, y)等于目标值z的参数组合。
最后,将找到的参数组合存储在结果集res中,并返回res作为最终的解答。
根据题目描述,我们需要通过调用CustomFunction接口中的方法来找到满足条件f(x, y) == z的所有正整数数对x和y。
我们可以利用函数单调递增的性质进行搜索。从左下角开始,设初始位置为(x, y) = (1, 1000),然后按照以下规则进行搜索:
- 如果
f(x, y) > z,则y减小1; - 如果
f(x, y) < z,则x增加1; - 如果
f(x, y) == z,则找到一个解,将(x, y)加入结果集。
重复上述步骤直到x或y超出范围。最后返回结果集即可。
相关文章:
leetcode1237. 找出给定方程的正整数解
1237. 找出给定方程的正整数解https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/ 难度中等 101 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满…...

sqlmap使用教程(6)-注入技术拓展
注入技术 选项--technique,可以用来指定SQL注入技术,默认为BEUSTQ。其中,B表示基于布尔盲注,E表示基于错误的盲注,U表示基于联合查询注入,S表示堆叠注入,T表示基于时间盲注,Q表示内联…...
苹果Find My市场需求火爆,伦茨科技ST17H6x芯片助力客户量产
苹果发布AirTag发布以来,大家都更加注重物品的防丢,苹果的 Find My 就可以查找 iPhone、Mac、AirPods、Apple Watch,如今的Find My已经不单单可以查找苹果的设备,随着第三方设备的加入,将丰富Find My Network的版图。产…...
3DMAX初级小白班第一课:菜单栏介绍
基本介绍 这里不可能一个一个选项全部教给大家(毕竟之后靠实操慢慢就记住了),只说一些相对需要注意的设置。 自定义-热键编辑器-热键设置 这里有你所需要的全部快捷键 自定义-自定义UI启动布局 将UI布局还原到启动的位置 自定义-通用单…...
Windows中Zookeeper与kafka的安装配置
一、Zookeeper安装与使用 1.安装包下载 直接在官网下载即可Apache ZooKeeper。 下载后直接解压到本地即可。 2.环境配置 1> 在目录中下增加data和log文件夹 2> 解压目录下的 conf 目录,将目录中的 zoo_sample.cfg 文件,复制一份,重…...
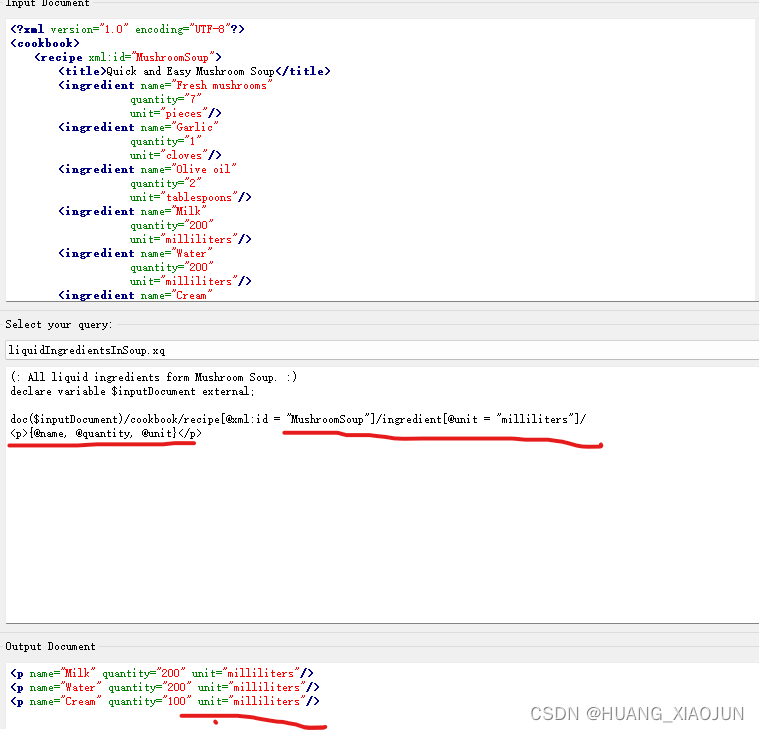
QT 官方例程阅读: XML Patterns 相关
标签用于在qt creator 中查询相关工程 一、标签 Schema Validator 模式验证器 就是根据 已知的XML 模式,验证输入的XML 文件格式是否匹配,不匹配可以输出不匹配位置 如下,,首先定义了contact 元素 的子元素列表,&…...

基于SpringBoot IP黑白名单的实现
业务场景 IP黑白名单是网络安全管理中常见的策略工具,用于控制网络访问权限,根据业务场景的不同,其应用范围广泛,以下是一些典型业务场景: 服务器安全防护: 黑名单:可以用来阻止已知的恶意IP地…...
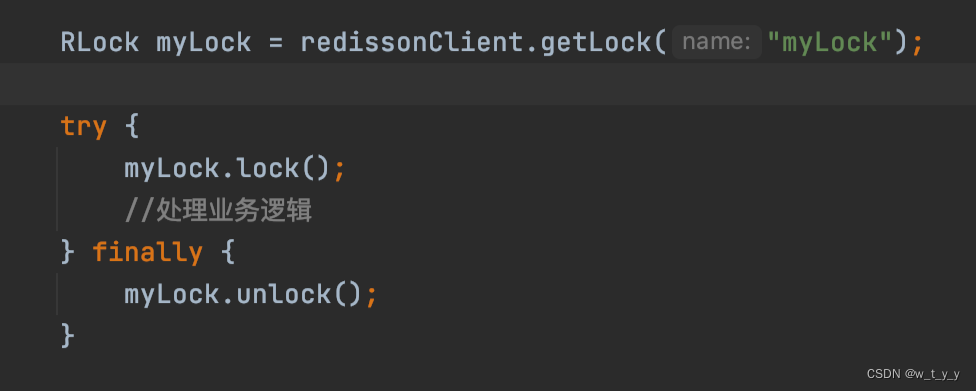
Redis客户端之Redisson(二)Redisson分布式锁
一、原理: Redisson并没有通过setNx命令来实现加锁,而是基于 Redis 看⻔狗机制,自己实现了一套分布式锁逻辑。 1、加锁机制: 二、使用方法:...
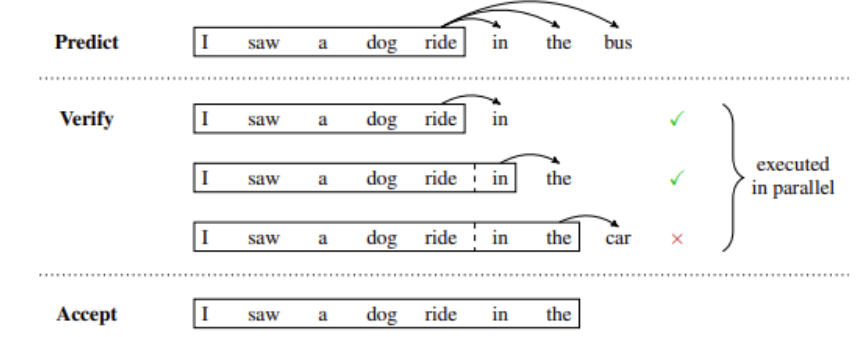
掌握大语言模型技术: 推理优化
掌握大语言模型技术_推理优化 堆叠 Transformer 层来创建大型模型可以带来更好的准确性、少样本学习能力,甚至在各种语言任务上具有接近人类的涌现能力。 这些基础模型的训练成本很高,并且在推理过程中可能会占用大量内存和计算资源(经常性成…...

git如何导出提交记录及修改的文件清单?
导出git提交日志及修改文件 # 所有人的提交记录 git log --pretty=format:"%ai,%an:%s" --since="10 day ago" >> ~/Desktop/commit10.log#某一个人的提交记录 git log --pretty=format:"%ai,%an:%s" --since="30 day ago" |...

从零开始:Ubuntu Server中MySQL 8.0的安装与Django数据库配置详解
Ubuntu系统纯净安装MySQL8.0 1、安装Mysql8.0 sudo apt install mysql-server2、检查MySQL状态 sudo systemctl status mysql如下所示看见Active: active (running)说明mysql状态正常 ● mysql.service - MySQL Community ServerLoaded: loaded (/lib/systemd/system/mysql…...

Vue基础知识
Vue Vue基础知识 v-bind:动态绑定属性值 Vue 修改,标签内也修改 在methods 中可以定义很多函数 在 data 中可以定义很多变量 v-if / v-show:对符合条件的元素进行展示 v-for:把数据遍历出现在网页中 案例 <!DOCTYPE html><html lang"e…...

瀑布流布局 (初版)
瀑布流布局 文章目录 瀑布流布局前言1. 背景2. 点⬇️🔗去体验效果如下图所示: 一、初版waterfall布局和问题暴露?1.效果图如下:2.暴露问题如下图所示:第一张问题图:第二张问题图: 3.HTML代码如…...

硕士毕业论文写作笔记
一、写作顺序 1.标题、研究问题、研究方法 2.文献综述(占比1/5-1/6) 3.论证章节 4.结论、不足、启示 5.处理图表、参考文献的格式 6.绪论或引言 7.摘要、关键词 8.查重、装订 http://【硕士毕业论文写不下去,多亏听了张博士的论文写…...
成本更低、更可控,云原生可观测新计费模式正式上线
云布道师 在上云开始使用云产品过程中,企业一定遇见过两件“讨厌”事: 难以理解的复杂计费逻辑,时常冒出“这也能收费”的感叹; 某个配置参数调节之后,云产品使用成本不可预估的暴涨。 可观测作为企业 IT 运维必须品…...

5.列表选择弹窗(BottomListPopup)
愿你出走半生,归来仍是少年! 环境:.NET 7、MAUI 从底部弹出的列表选择弹窗。 1.布局 <?xml version"1.0" encoding"utf-8" ?> <toolkit:Popup xmlns"http://schemas.microsoft.com/dotnet/2021/maui"xmlns…...
Head first design patterns原型模式(c++))
(十三)Head first design patterns原型模式(c++)
原型模式 原型模式就是就是对对象的克隆。有一些私有变量外界难以访问,而原型模式可以做到对原型一比一的复刻。 其关键代码为下面的clone方法。此方法将本对象进行复制传递出去。 class ConcretePrototype1 : public Prototype{ public:ConcretePrototype1(stri…...
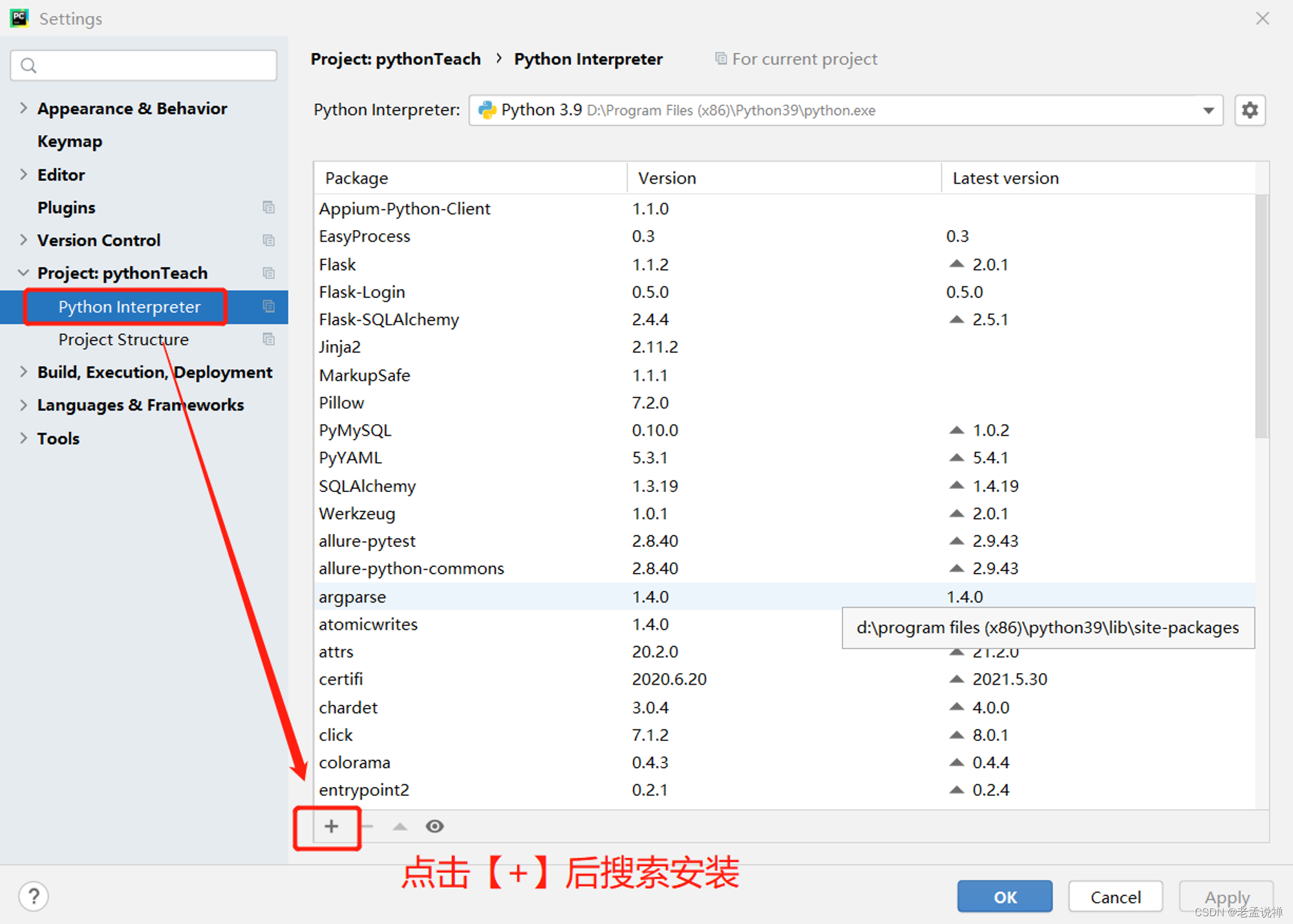
Python基础之数据库操作
一、安装第三方库PyMySQL 1、在PyCharm中通过 【File】-【setting】-【Python Interpreter】搜索 PyMySQL进行安装 2、通过PyCharm中的 Terminal 命令行 输入: pip install PyMySQL 注:通过pip安装,可能会提示需要更新pip,这时可执行&#…...
redis-发布缓存
一.redis的发布订阅 什么 是发布和订阅 Redis 发布订阅 (pub/sub) 是一种消息通信模式:发送者 (pub) 发送消息,订阅者 (sub) 接收消息。 Redis 客户端可以订阅任意数量的频道。 Redis的发布和订阅 客户端订阅频道发布的消息 频道发布消息 订阅者就可…...

Stata17安装教程
文章目录 **Stata17安装教程**前言系统要求Windows:macOS:Linux: 软件下载正式安装1.下载Stata 17安装包2.双击Stata17.exe开启安装3.接受同意条款,然后继续安装4.选择想要安装的版本,Stata BE为基础版、Stata SE为特别…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
