马尔可夫预测(Python)
马尔科夫链(Markov Chains)
从一个例子入手:假设某餐厅有A,B,C三种套餐供应,每天只会是这三种中的一种,而具体是哪一种,仅取决于昨天供应的哪一种,换言之,如果知道今天供应了什么,就可以用某种方式预测明天将会供应什么。
例如,今天供应的是A,那么明天有60%概率供应B,我们可以用一条由A向B的有向边来表示,边权是概率。于是我们可以用图来表示这种关系:
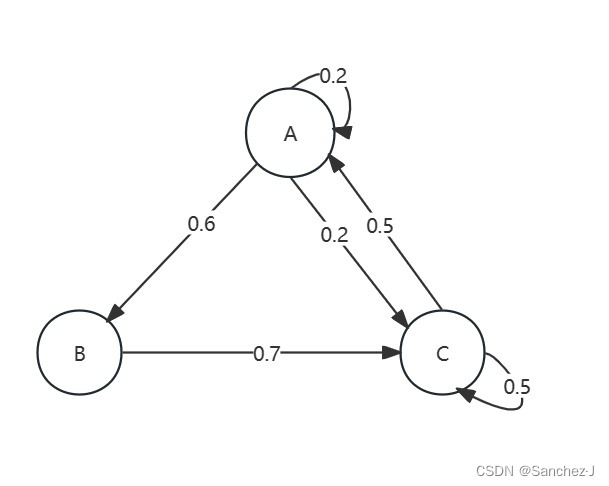
这就是一个马尔科夫链。
马尔科夫链的一个重要状态就是未来状态只取决于现在状态而与过去无关。
也就是有
例如考虑已知一个供应序列[B,A,B],那么第4天供应C的概率是多少?由马尔可夫性质,我们只需要考虑第3天,因此概率就是70%。
下面我们在链上做随机漫步(Random Walk),比如得到结果[A, B, A, C, A, C, C, C, A, B],现在我们想要求出每种套餐的概率,直接用频率分布近似,而长期下来,这些概率(可能)会收敛到某些特定值,这种概率分布叫做稳态分布。
我们亦可用线性代数来求出稳态的概率分布,对于有向图,我们可以转化为邻接矩阵:
我们用一个行向量来代表状态的概率,假设我们从B状态开始,则有
当我们将这个行向量和矩阵相乘,我们得到了矩阵的第二行,更广义地,我们得到了未来的状态。
依次类推,那么我们可以说,如果在某一次达到了稳态,那么输出的行向量应当等于输入的行向量,于是我们得到了这个在线性代数中熟悉的表达式
因此其实是矩阵的特征向量,特征值等于1,此外
的元素还需要满足归一性,也即全部元素之和等于1。
由此我们可以解出这个稳态:,这个结果和直接模拟得到的相符合。
这个结果告诉我们,餐厅整体上会在大概35%的时间供应A,21%的时间供应B,剩下时间供应C。
由此我们也可以看出可能存在多个稳态,取决于有多少个满足条件的特征向量。
现在考虑下面这个马尔科夫链:

我们会发现对于状态0只要离开就不可能再回去了,这种不可被其他状态达到的情况我们称为暂态(transient)。
而对于状态1、2离开后是可以回来的,称为常返状态(Recurrent)
而当存在暂态时,我们称这个马尔科夫链是可约的;反之称不可约链。
这里我们如果把0->1这条边删去,可以得到两个更小的不可约链。
现在考虑下面这个马尔科夫链

考虑这个问题:
从状态i到状态j共n步的概率()是多大?
可以先考虑简单的,显然等于
而对于,我们需要考虑所有可能的路径,并将概率相加:
这个表达式其实是两个向量乘积
由此我们可以总结
进一步
这样的总结是根据经验的归纳,不能保证正确。
但确实是正确的,根据是Chapman-Kolmogorov定理,之所以能使用,是因为马尔可夫性质。
该定理表述如下:
现在我们从另一个视角来看稳态分布,我们让n趋于无穷大
每一行都收敛到同一个行向量,这就是这个马尔科夫链的静态分布。
比如对于
,对于不同的i其值是不变的,换言之,不依赖于开始的状态,这恰恰符合马尔可夫性质。
隐马尔科夫链(Hidden Markov Model)
仍然从例子入手:
Jack 所住的地方只有三种天气A,B,C,任何一天只会出现一种天气,明天天气只和今天天气相关。 假设Jack每天有两种可能的心情a、b,心情取决于天气。如下图
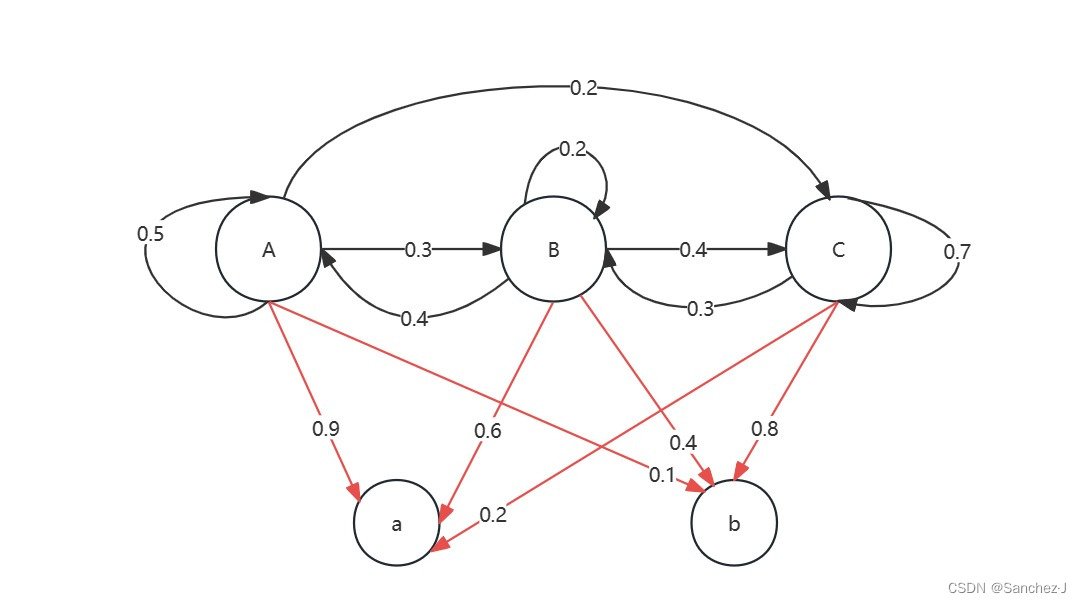
现在我们不知道某一天的天气情况,但是我们可以了解Jack的情绪,因此说马尔科夫链的状态是隐藏的,我们可以观察到一些依赖于这些状态的变量。可以说,隐马尔可夫模型就是一个普通的马尔科夫链和一组观测变量构成,即
HMM = HiddenMC + Observed Variables
注意:Jack的情绪只和当天的天气有关而和昨天的情绪无关
同样我们可以用矩阵表示
转移矩阵:
发射矩阵(记录观测变量相应概率的矩阵):
现在考虑连续三天的情况

这里先假设我们知道天气情况,那么这种情况的概率我们可以算出来:
其中第一项需要用求平稳分布得到,其余项可以直接从矩阵读出。
现在我们隐藏状态,只看观察变量的序列,最有可能的状态序列是什么?
要解决这个问题,我们需要计算每个序列的概率,找出概率最大的序列,而最终找出来确实是CBC这个序列。
Python模板代码
详见注释
from hmmlearn.hmm import GaussianHMM
# 导入 GaussianHMM 类,这是 hmmlearn 库中用于高斯混合模型(Gaussian Hidden Markov Model)的类。
import numpy as np
startprob = np.array([0.6, 0.3, 0.1, 0.0])
# 建一个 NumPy 数组 startprob,表示 HMM 模型的初始状态概率。
transmat = np.array([[0.7, 0.2, 0.0, 0.1],[0.3, 0.5, 0.2, 0.0],[0.0, 0.3, 0.5, 0.2],[0.2, 0.0, 0.2, 0.6]])
# 创建一个 NumPy 数组 transmat,表示 HMM 模型的状态转移矩阵。
means = np.array([[0.0, 0.0],[0.0, 11.0],[9.0, 10.0],[11.0, -1.0]])
# 表示每个隐藏状态的均值。
covars = .5 * np.tile(np.identity(2), (4, 1, 1))
# 表示每个隐藏状态的协方差矩阵。这里使用了 np.tile 来生成相同的协方差矩阵。
hmm = GaussianHMM(n_components=4, covariance_type='full')
# 创建一个 GaussianHMM 对象,指定模型有 4 个隐藏状态,并使用完整的协方差矩阵
hmm.startprob_ = startprob
# 设置 HMM 模型对象的初始状态概率。
hmm.transmat_ = transmat
# 设置 HMM 模型对象的状态转移矩阵。
hmm.means_ = means
# 设置 HMM 模型对象的均值。
hmm.covars_ = covars
# 设置 HMM 模型对象的协方差矩阵。
seen = np.array([[1.1, 2.0], [-1, 2.0], [3, 7]])
# seen表示观察到的数据序列。
logprob, state = hmm.decode(seen, algorithm="viterbi")
# 使用 Viterbi 算法对给定的观察数据序列进行解码,返回对数概率和对应的状态序列。
print(state)
print(hmm.score(seen))
相关文章:
马尔可夫预测(Python)
马尔科夫链(Markov Chains) 从一个例子入手:假设某餐厅有A,B,C三种套餐供应,每天只会是这三种中的一种,而具体是哪一种,仅取决于昨天供应的哪一种,换言之&#…...
双向队列的创建队首与队尾的操作deque()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 双向队列的创建 队首与队尾的操作 deque() [太阳]选择题 请问以下代码输出的结果是? from collections import deque print("【创建双向队列】d deque()") d deque(…...
一、MongoDB、express的安装和基本使用
数据库【Sqlite3、MongoDB、Mysql】简介&小记 Sqlite3: SQLite3是一个轻量级的数据库系统,它被设计成嵌入式数据库。这意味着它是一个包含在应用程序中的数据库,而不是独立运行的系统服务。适用场景:如小型工具、游戏、本地…...

被困住了——如何从层级结构中获取子集
大家好,我是欧阳方超,我被一个问题困住了。 事情是这样的,与第三方平台对接时,第三方接口返回了一个具有层级结构的列表,比如下面这种结构: [{"id": 1,"name": "Root Category 1…...
leetcode1237. 找出给定方程的正整数解
1237. 找出给定方程的正整数解https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/ 难度中等 101 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满…...

sqlmap使用教程(6)-注入技术拓展
注入技术 选项--technique,可以用来指定SQL注入技术,默认为BEUSTQ。其中,B表示基于布尔盲注,E表示基于错误的盲注,U表示基于联合查询注入,S表示堆叠注入,T表示基于时间盲注,Q表示内联…...
苹果Find My市场需求火爆,伦茨科技ST17H6x芯片助力客户量产
苹果发布AirTag发布以来,大家都更加注重物品的防丢,苹果的 Find My 就可以查找 iPhone、Mac、AirPods、Apple Watch,如今的Find My已经不单单可以查找苹果的设备,随着第三方设备的加入,将丰富Find My Network的版图。产…...
3DMAX初级小白班第一课:菜单栏介绍
基本介绍 这里不可能一个一个选项全部教给大家(毕竟之后靠实操慢慢就记住了),只说一些相对需要注意的设置。 自定义-热键编辑器-热键设置 这里有你所需要的全部快捷键 自定义-自定义UI启动布局 将UI布局还原到启动的位置 自定义-通用单…...
Windows中Zookeeper与kafka的安装配置
一、Zookeeper安装与使用 1.安装包下载 直接在官网下载即可Apache ZooKeeper。 下载后直接解压到本地即可。 2.环境配置 1> 在目录中下增加data和log文件夹 2> 解压目录下的 conf 目录,将目录中的 zoo_sample.cfg 文件,复制一份,重…...
QT 官方例程阅读: XML Patterns 相关
标签用于在qt creator 中查询相关工程 一、标签 Schema Validator 模式验证器 就是根据 已知的XML 模式,验证输入的XML 文件格式是否匹配,不匹配可以输出不匹配位置 如下,,首先定义了contact 元素 的子元素列表,&…...

基于SpringBoot IP黑白名单的实现
业务场景 IP黑白名单是网络安全管理中常见的策略工具,用于控制网络访问权限,根据业务场景的不同,其应用范围广泛,以下是一些典型业务场景: 服务器安全防护: 黑名单:可以用来阻止已知的恶意IP地…...
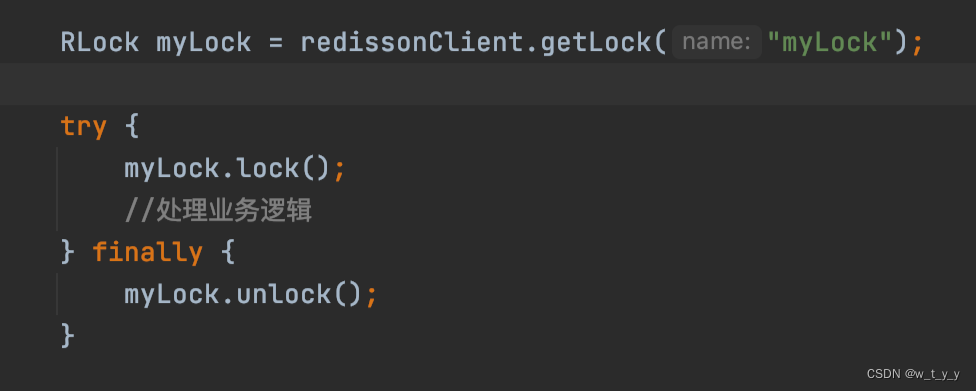
Redis客户端之Redisson(二)Redisson分布式锁
一、原理: Redisson并没有通过setNx命令来实现加锁,而是基于 Redis 看⻔狗机制,自己实现了一套分布式锁逻辑。 1、加锁机制: 二、使用方法:...
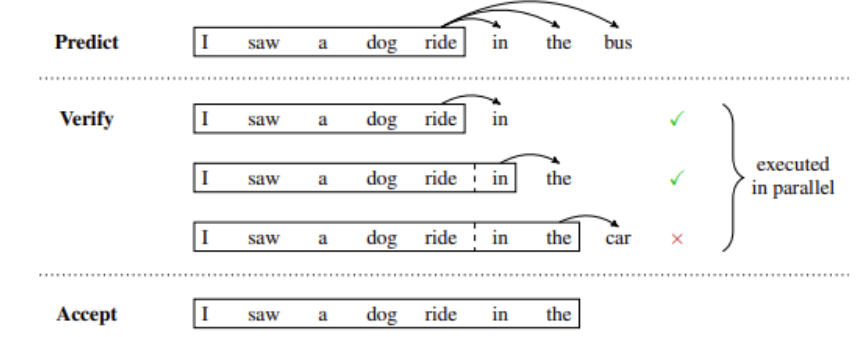
掌握大语言模型技术: 推理优化
掌握大语言模型技术_推理优化 堆叠 Transformer 层来创建大型模型可以带来更好的准确性、少样本学习能力,甚至在各种语言任务上具有接近人类的涌现能力。 这些基础模型的训练成本很高,并且在推理过程中可能会占用大量内存和计算资源(经常性成…...

git如何导出提交记录及修改的文件清单?
导出git提交日志及修改文件 # 所有人的提交记录 git log --pretty=format:"%ai,%an:%s" --since="10 day ago" >> ~/Desktop/commit10.log#某一个人的提交记录 git log --pretty=format:"%ai,%an:%s" --since="30 day ago" |...

从零开始:Ubuntu Server中MySQL 8.0的安装与Django数据库配置详解
Ubuntu系统纯净安装MySQL8.0 1、安装Mysql8.0 sudo apt install mysql-server2、检查MySQL状态 sudo systemctl status mysql如下所示看见Active: active (running)说明mysql状态正常 ● mysql.service - MySQL Community ServerLoaded: loaded (/lib/systemd/system/mysql…...

Vue基础知识
Vue Vue基础知识 v-bind:动态绑定属性值 Vue 修改,标签内也修改 在methods 中可以定义很多函数 在 data 中可以定义很多变量 v-if / v-show:对符合条件的元素进行展示 v-for:把数据遍历出现在网页中 案例 <!DOCTYPE html><html lang"e…...

瀑布流布局 (初版)
瀑布流布局 文章目录 瀑布流布局前言1. 背景2. 点⬇️🔗去体验效果如下图所示: 一、初版waterfall布局和问题暴露?1.效果图如下:2.暴露问题如下图所示:第一张问题图:第二张问题图: 3.HTML代码如…...

硕士毕业论文写作笔记
一、写作顺序 1.标题、研究问题、研究方法 2.文献综述(占比1/5-1/6) 3.论证章节 4.结论、不足、启示 5.处理图表、参考文献的格式 6.绪论或引言 7.摘要、关键词 8.查重、装订 http://【硕士毕业论文写不下去,多亏听了张博士的论文写…...
成本更低、更可控,云原生可观测新计费模式正式上线
云布道师 在上云开始使用云产品过程中,企业一定遇见过两件“讨厌”事: 难以理解的复杂计费逻辑,时常冒出“这也能收费”的感叹; 某个配置参数调节之后,云产品使用成本不可预估的暴涨。 可观测作为企业 IT 运维必须品…...

5.列表选择弹窗(BottomListPopup)
愿你出走半生,归来仍是少年! 环境:.NET 7、MAUI 从底部弹出的列表选择弹窗。 1.布局 <?xml version"1.0" encoding"utf-8" ?> <toolkit:Popup xmlns"http://schemas.microsoft.com/dotnet/2021/maui"xmlns…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
