Vue2 props组件通信
一、父组件向子组件传值
1、流程图
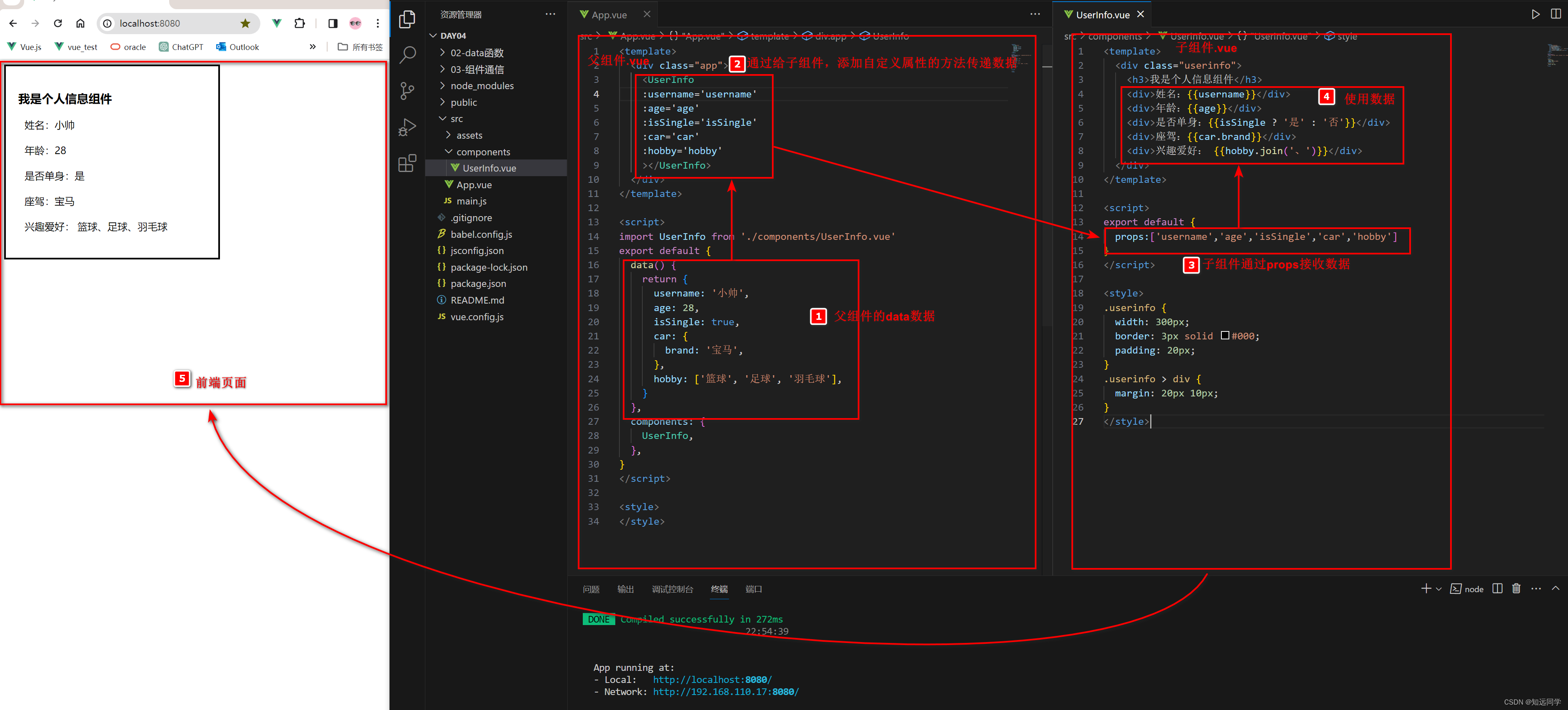
2、父组件代码
<template><div class="app"><UserInfo:username='username':age='age':isSingle='isSingle':car='car':hobby='hobby'></UserInfo></div>
</template><script>
import UserInfo from './components/UserInfo.vue'
export default {data() {return {username: '小帅',age: 28,isSingle: true,car: {brand: '宝马',},hobby: ['篮球', '足球', '羽毛球'],}},components: {UserInfo,},
}
</script><style>
</style>3、子组件代码
<template><div class="userinfo"><h3>我是个人信息组件</h3><div>姓名:{{username}}</div><div>年龄:{{age}}</div><div>是否单身:{{isSingle ? '是' : '否'}}</div><div>座驾:{{car.brand}}</div><div>兴趣爱好: {{hobby.join('、')}}</div></div>
</template><script>
export default {props:['username','age','isSingle','car','hobby']
}
</script><style>
.userinfo {width: 300px;border: 3px solid #000;padding: 20px;
}
.userinfo > div {margin: 20px 10px;
}
</style>
相关文章:

Vue2 props组件通信
一、父组件向子组件传值 1、流程图 2、父组件代码 <template><div class"app"><UserInfo:usernameusername:ageage:isSingleisSingle:carcar:hobbyhobby></UserInfo></div> </template><script> import UserInfo from .…...
重构改善既有代码的设计-学习(三):重新组织数据
1、拆分变量(Split Variable) 有些变量用于保存一段冗长代码的运算结果,以便稍后使用。这种变量应该只被赋值一次。 如果它们被赋值超过一次,就意味它们在函数中承担了一个以上的责任。如果变量承担多个责任,它就应该被…...
|广告效果测评方法)
群狼调研(长沙品牌忠诚度测试)|广告效果测评方法
广告效果测评方法可以根据具体的目标和需求而有所差异,以下是一些常见的广告效果测评方法: 1.品牌调研和调查:通过定量或定性的调研和调查方法,评估广告对品牌认知、品牌形象和品牌偏好的影响,包括品牌知名度、品牌关联…...

Gradle学习笔记:Gradle的使用方法
文章目录 1.初始化项目2.构建脚本语言选择3.项目命名4.项目构建过程 1.初始化项目 创建一个test空文件夹,在该文件夹下打开终端,并执行命令:gradle init. 会有一个选项让你选择项目的类型。下面是每个选项的含义和用途: basic&am…...

少儿编程 2023年12月电子学会图形化编程等级考试Scratch二级真题解析(选择题)
2023年12月scratch编程等级考试二级真题 选择题(共25题,每题2分,共50分) 1、在制作推箱子游戏时,地图是用数字形式储存在电脑里的,下图是一个推箱子地图,地图表示如下:第一行( 111111)第二行( 132231) 第三行( 126621) 第四行( ) 第五行( 152321) 第六行( 111111 ) 根…...
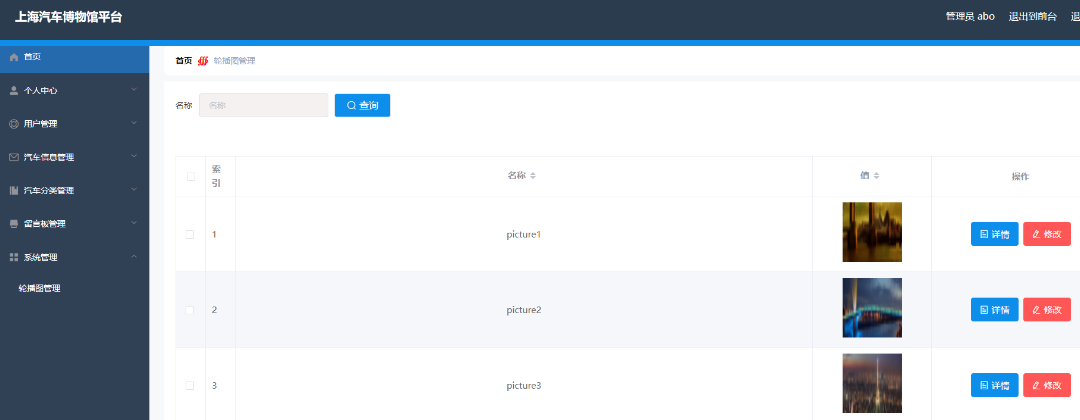
基于Java+SpringMvc+vue+element实现上海汽车博物馆平台
基于JavaSpringMvcvueelement实现上海汽车博物馆平台 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承接各种定制系统 …...

Sybase PowerDesigner15安装配置
1,软件介绍 Power Designer 是Sybase公司的CASE工具集,使用它可以方便地对管理信息系统进行分析设计,他几乎包括了数据库模型设计的全过程。利用Power Designer可以制作数据流程图、概念数据模型、物理数据模型,还可以为数据仓…...

基于物联网设计的水稻田智能灌溉系统(STM32+华为云IOT)
一、项目介绍 随着科技的不断发展和人们生活水平的提高,农业生产也逐渐向智能化、高效化的方向发展。水稻作为我国主要的粮食作物之一,其生长过程中的灌溉管理尤为重要。传统的灌溉方式往往依赖于人工观察和控制,不仅效率低下,而…...

【数据结构】数据结构初识
前言: 数据结构是计算存储,组织数据的方式。数据结构是指相互间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。 Data Structure Vi…...
)
java多线程测试websocket demo(使用文件流)
这个demo主要是利用Java多线程来测试WebSocket通信。首先,创建一个WebSocket服务器和客户端,然后使用多线程来模拟多个客户端同时连接服务器进行通信。通过多线程测试,可以验证WebSocket通信的并发性能和稳定性。同时,可以通过多线…...

Tosei 自助网络店铺管理系统network_test.php_RCE漏洞复现
简介 Tosei 自助洗衣机是日本一家公司的产品,在 network_test.php 文件存在命令执行 漏洞复现 FOFA语法: body="tosei_login_check.php" 主要是日本 访问界面如下所示: 验证POC: /cgi-bin/network_test.php 拼接访问url: https://ip:port/cgi-bin/network_tes…...

uni-app 国际化
vue i18n v9的迁移后的$t()无法获取数组、对象 http://t.csdnimg.cn/WkCHy api:vue i18n [intlify] Not found ‘language’ key in ‘zh-Hans’ locale messages. [intlify] Fall back to translate ‘language’ key with ‘zh’ locale. [intlify] Not found ‘languag…...
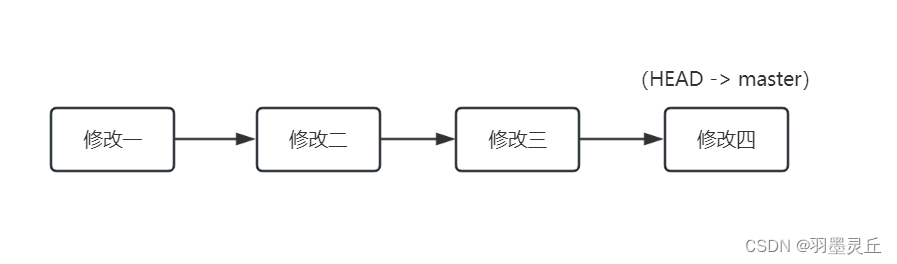
git:git reset 和 git revert
在使用 git 进行项目开发的过程中,有时会出现错误提交的情况,这时就需要能够撤销错误的提交,将代码恢复到提交之前的样子。根据不同情况,可以使用 git reset 或 git revert 命令。 一. git reset git reset 的原理是修改 HEAD 的…...
)
LeetCode:670. 最大交换(Java 贪心)
目录 670. 最大交换 题目描述: 实现代码与解析; 贪心 原理思路: 670. 最大交换 题目描述: 给定一个非负整数,你至多可以交换一次数字中的任意两位。返回你能得到的最大值。 示例 1 : 输入: 2736 输出: 7236 解释…...

【STM32】STM32学习笔记-Unix时间戳(41)
00. 目录 文章目录 00. 目录01. Unix时间戳02. UTC/GMT03. 时间戳转换04. C 标准库 <time.h>05. 时间相关函数示例5.1 time函数5.2 gmtime函数5.3 localtime函数5.4 mktime函数5.5 ctime函数5.6 asctime函数5.7 strftime函数 06. 预留07. 附录 01. Unix时间戳 •Unix 时…...

2016年认证杯SPSSPRO杯数学建模B题(第一阶段)低分辨率下看世界全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 B题 低分辨率下看世界 原题再现: 数码摄像技术被广泛使用于多种场合中。有时由于客观条件的限制,拍摄设备只能在较低的分辨率下成像。为简单起见,我们只考虑单色成像。假设成像的分辨率为 32 64,…...
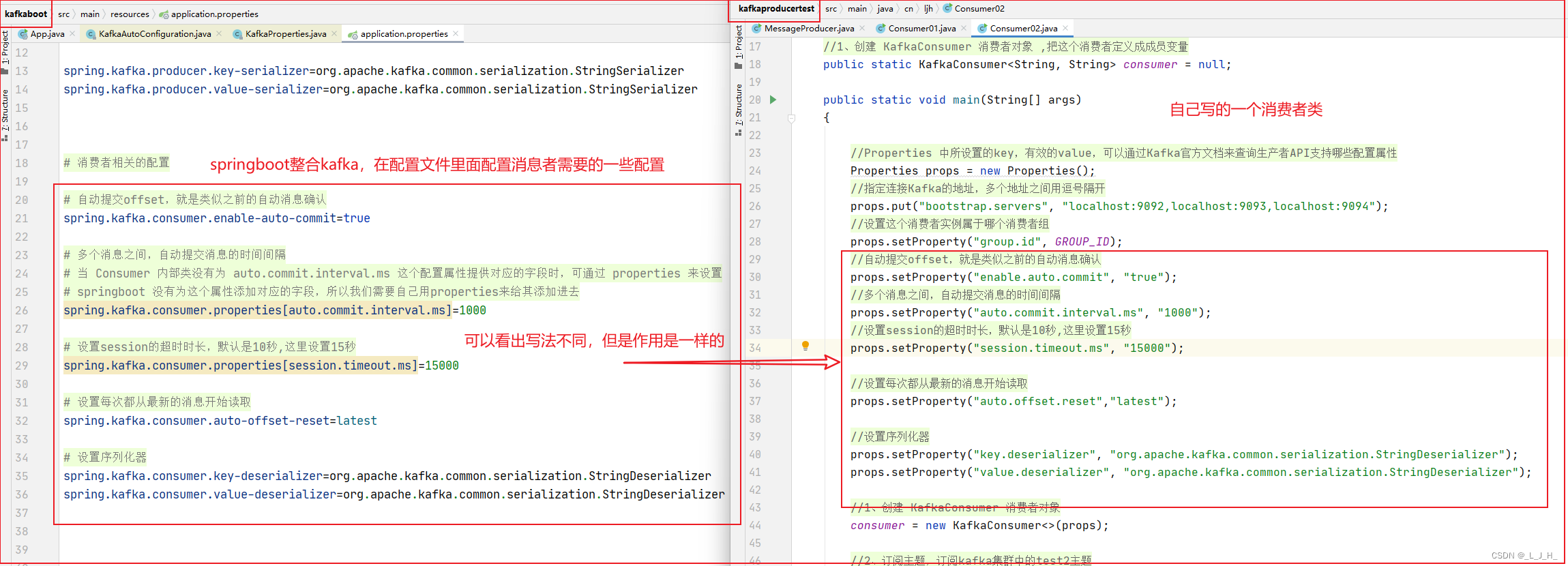
16、Kafka ------ SpringBoot 整合 Kafka (配置 Kafka 属性 及对应的 属性处理类 解析)
目录 配置 Kafka 及对应的 属性处理类配置KafkaKafka配置属性的约定代码演示生产者相关的配置消费者相关的配置 代码(配置文件)application.properties 配置 Kafka 及对应的 属性处理类 配置Kafka spring.kafka.* 开头的配置属性,这些属性将由…...

【蓝桥杯选拔赛真题61】python偶数平方 第十五届青少年组蓝桥杯python 选拔赛比赛真题解析
目录 python偶数平方 一、题目要求 1、编程实现 2、输入输出...

智能语音识别源码系统+语义理解+对话管理+语音合成 带完整的搭建教程
人工智能技术的不断发展,智能语音识别技术逐渐成为人们日常生活和工作中不可或缺的一部分。然而,目前市场上的智能语音识别产品大多存在一定的局限性,如识别率不高、功能单一等。为了解决这些问题,罗峰给大家分享一款基于智能语音…...

cdh6.3.2的hive配udf
背景 大数据平台的租户要使用udf,他们用beeline连接, 意味着要通过hs2,但如果有多个hs2,各个hs2之间不能共享,需要先把文件传到hdfs,然后手动在各hs2上create function。之后就可以永久使用了,…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
