[蓝桥杯]真题讲解:冶炼金属(暴力+二分)
蓝桥杯真题视频讲解:冶炼金属(暴力做法与二分做法)
- 一、视频讲解
- 二、暴力代码
- 三、正解代码
一、视频讲解
视频讲解
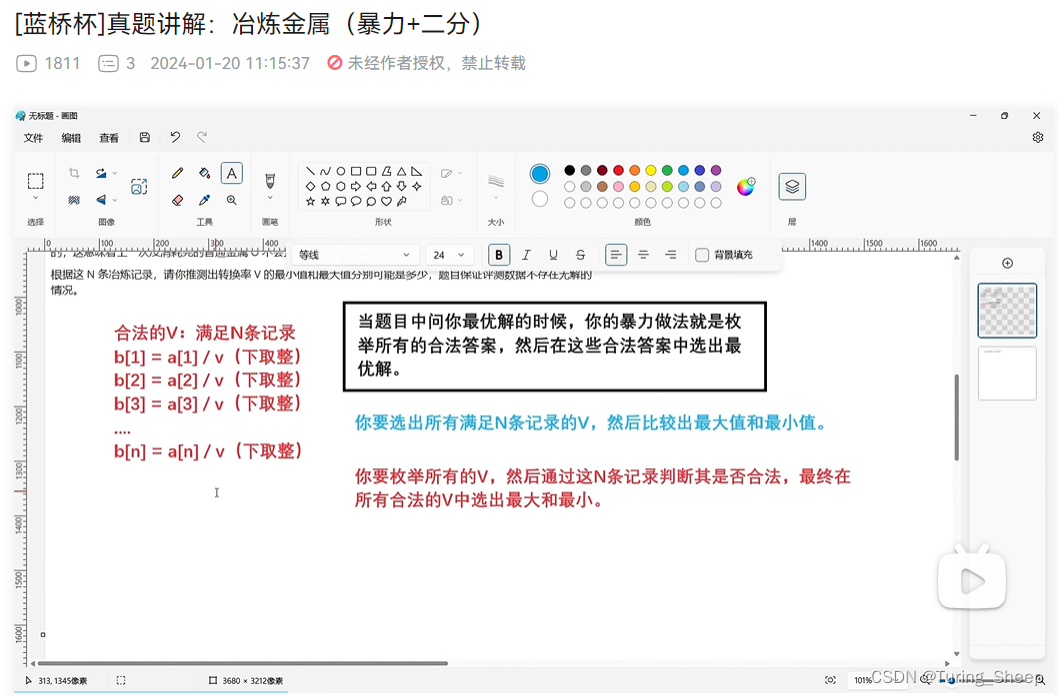
二、暴力代码
//暴力代码
#include<bits/stdc++.h>
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
using namespace std;
const int N = 1e4 + 10;void solve()
{int n; cin >> n;vector<int>a(n), b(n);//创建数组for(int i = 0; i < n; i ++)cin >> a[i] >> b[i];for(int i = 1; i <= 1e6; i ++)//枚举的转化率V{bool flag = true;//标记一下当前的V是否合法for(int j = 0; j < n; j ++){if(b[j] != (a[j] / i)){flag = false;break;}}if(flag){cout << i << " ";break;}}for(int i = 1e6; i >= 1; i --){bool flag = true;for(int j = 0; j < n; j ++){if(b[j] != (a[j] / i)){flag = false;break;}}if(flag){cout << i << " ";break;}}}signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;//cin >> t;while(t--)solve();
}三、正解代码
//冶炼金属:二分
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e4 + 10;
int a[N], b[N];
int n;bool check_min(int mid)
{for(int i = 0; i < n; i ++){if(b[i] < a[i] / mid)return false;}return true;
}bool check_max(int mid)
{for(int i = 0; i < n; i ++)if(b[i] > a[i] / mid)return false;return true;
}void solve()
{cin >> n;for(int i = 0; i < n; i ++)cin >> a[i] >> b[i];//求最小值。int lmin = 1, rmin = 1e9;while(lmin < rmin){int mid = lmin + rmin >> 1;if(check_min(mid))rmin = mid;elselmin = mid + 1;}//求最大值。int lmax = 1, rmax = 1e9;while(lmax < rmax){int mid = lmax + rmax + 1 >> 1;if(check_max(mid))lmax = mid;elsermax = mid - 1;}cout << lmin << " " << lmax << endl;
}signed main()
{ios::sync_with_stdio(0);int t = 1;// cin >> t;while(t--)solve();
}相关文章:

[蓝桥杯]真题讲解:冶炼金属(暴力+二分)
蓝桥杯真题视频讲解:冶炼金属(暴力做法与二分做法) 一、视频讲解二、暴力代码三、正解代码 一、视频讲解 视频讲解 二、暴力代码 //暴力代码 #include<bits/stdc.h> #define endl \n #define deb(x) cout << #x << &qu…...

Fastbee开源物联网项目RoadMap
架构优化 代码简化业务&协议解耦关键组件支持横向拓展网络协议支持横向拓展,包括:mqtt broker,tcp,coap,udp,sip等协议插件化编码脚本化业务代码模版化消息总线 功能优化 网关/子网关:上线,绑定,拓扑࿰…...
Linux文件管理技术实践
shell shell的种类(了解) shell是用于和Linux内核进行交互的一个程序,他的功能和window系统下的cmd是一样的。而且shell的种类也有很多常见的有c shell、bash shell、Korn shell等等。而本文就是使用Linux最常见的bash shell对Linux常见指令展开探讨。 内置shell…...

Python如何按指定列的空值删除行?
目录 1、按指定列的空值删除行2、滑动窗口按指定列的值填充最前面的缺失值 1、按指定列的空值删除行 数据准备: df pd.DataFrame({C1: [1, 2, 3, 4], C2: [A, np.NaN, C, D], C3: [V1, V2, V3, np.NaN]}) print(df.to_string()) C1 C2 C3 0 1 A V1 1 …...

【云原生】Docker的镜像创建
目录 1.基于现有镜像创建 (1)首先启动一个镜像,在容器里做修改 编辑(2)然后将修改后的容器提交为新的镜像,需要使用该容器的 ID 号创建新镜像 实验 2.基于本地模板创建 3&am…...
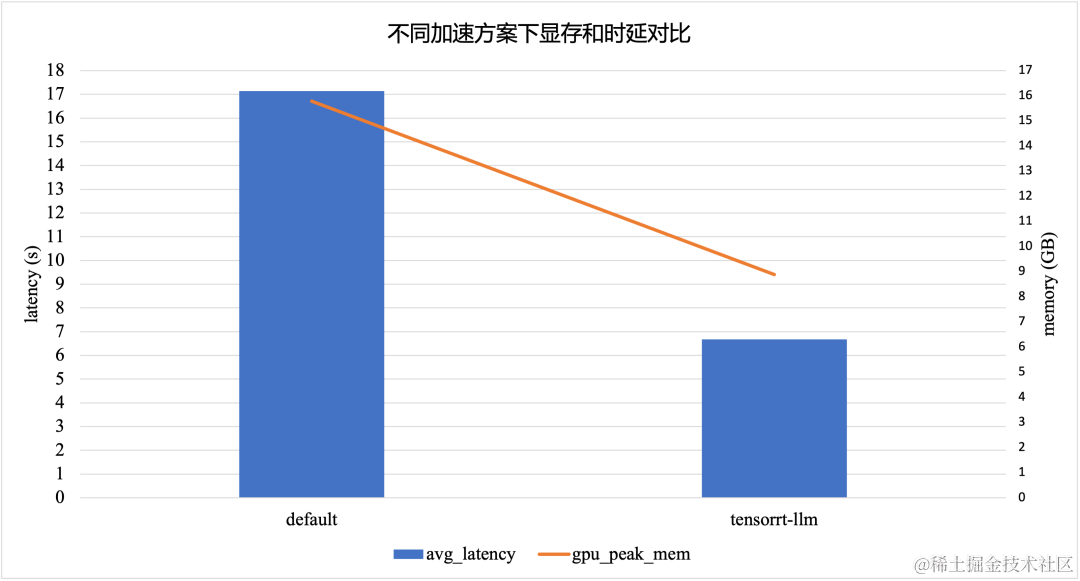
大语言模型推理提速:TensorRT-LLM 高性能推理实践
作者:顾静 TensorRT-LLM 如何提升 LLM 模型推理效率 大型语言模型(Large language models,LLM)是基于大量数据进行预训练的超大型深度学习模型。底层转换器是一组神经网络,这些神经网络由具有 self-attention 的编码器和解码器组…...

全面理解“张量”概念
1. 多重视角看“张量” 张量(Tensor)是一个多维数组的概念,在不同的学科领域中有不同的应用和解释: 物理学中的张量: 在物理学中,张量是一个几何对象,用来表示在不同坐标系下变换具有特定规律的…...
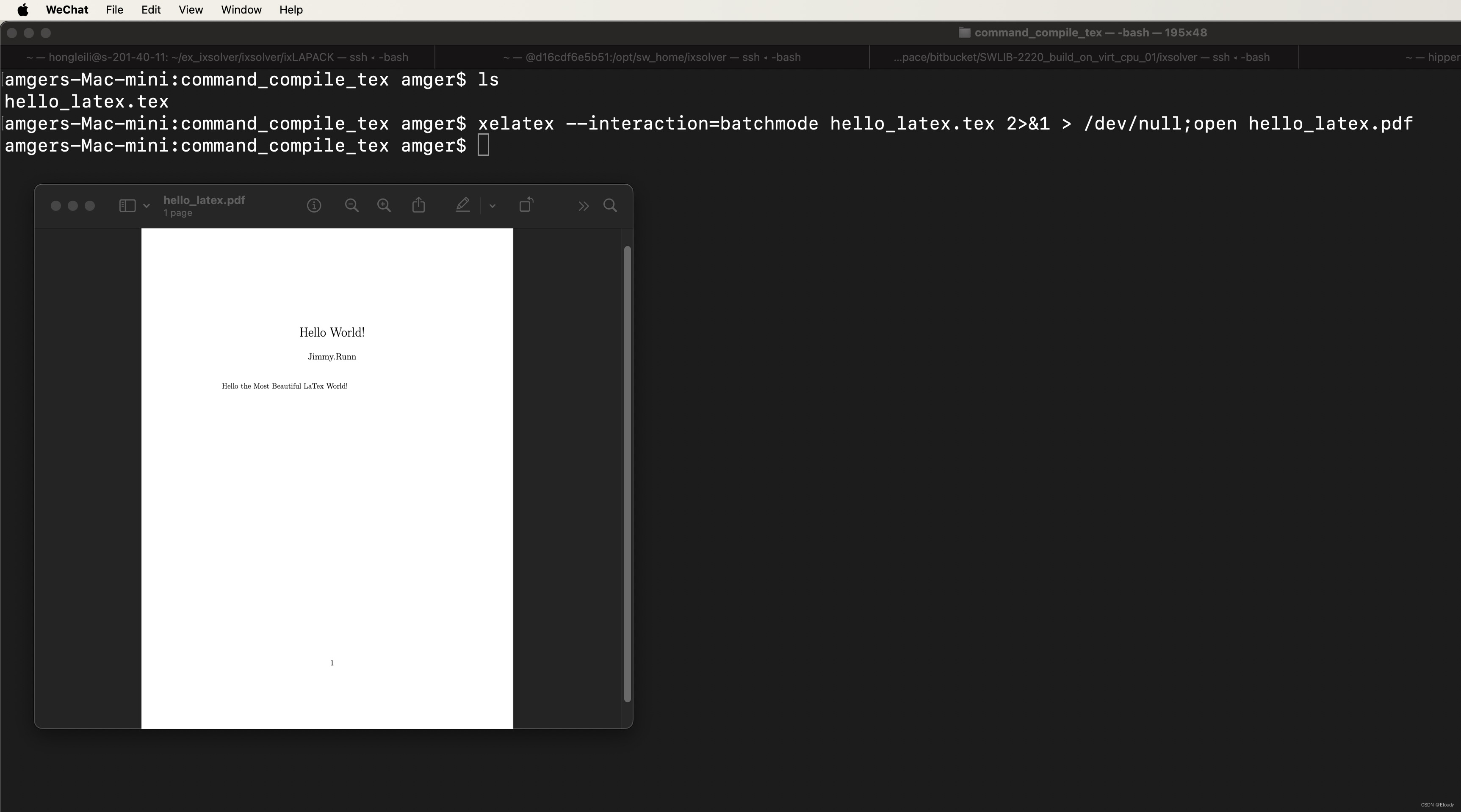
MacOS X 安装免费的 LaTex 环境
最近把工作终端一步步迁移到Mac上来了,搭了个 Latex的环境,跟windows上一样好用。 首先,如果是 intel 芯片的 macOS,那么可以使用组合1, 如果是 M1、M2 或 M3 芯片或者 intel 芯片的 Mac book,则应该使用…...

深入Amazon S3:实战指南
Amazon S3(Simple Storage Service)是AWS(Amazon Web Services)提供的一项强大的云存储服务,广泛用于存储和检索各种类型的数据。本篇实战指南将深入介绍如何在实际项目中充分利用Amazon S3的功能,包括存储桶的创建、对象的管理、权限控制、版本控制、日志记录等方面的实…...
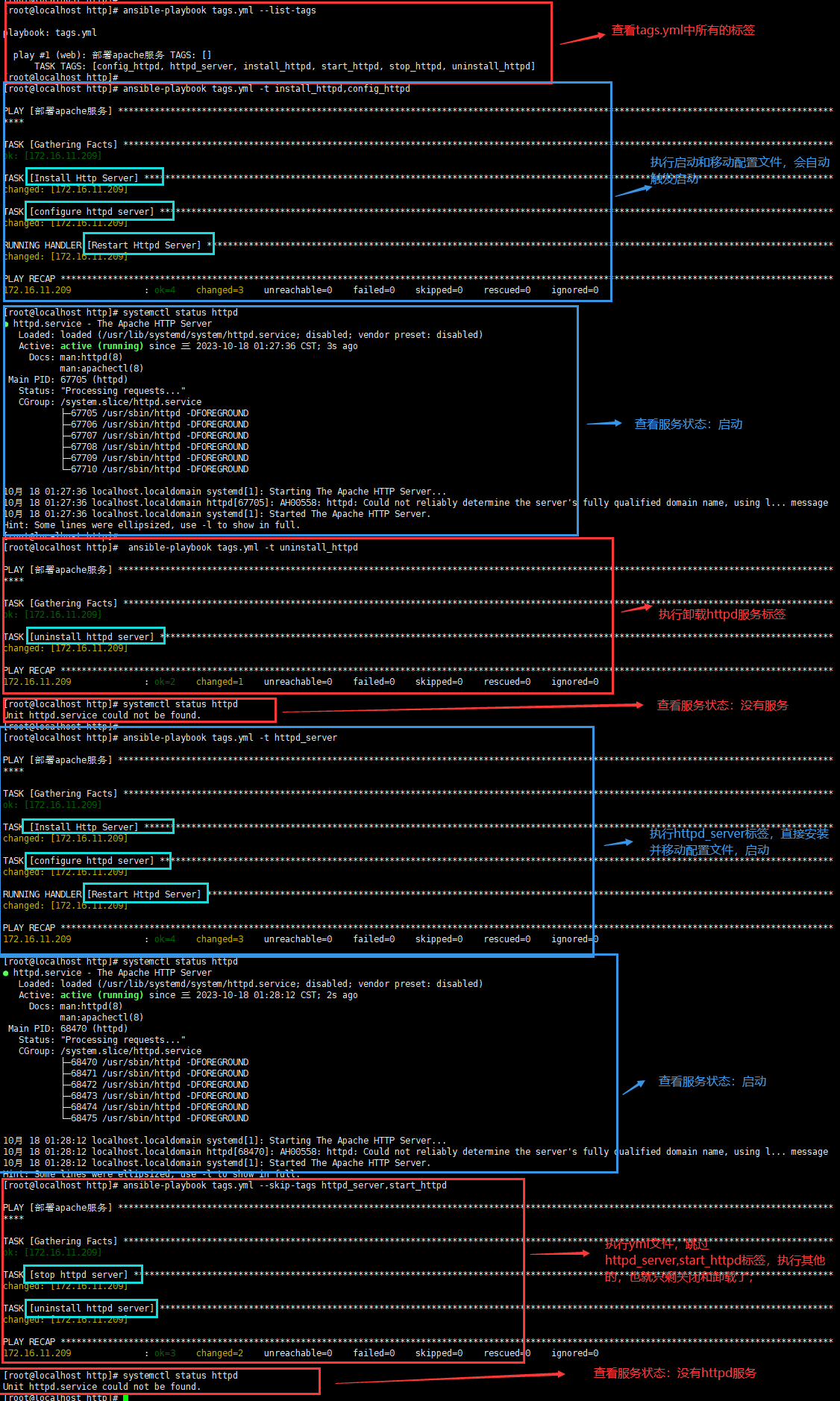
Ansible自动化运维(三)Playbook 模式详解
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...

LCS板子加逆向搜索
LCS 题面翻译 题目描述: 给定一个字符串 s s s 和一个字符串 t t t ,输出 s s s 和 t t t 的最长公共子序列。 输入格式: 两行,第一行输入 s s s ,第二行输入 t t t 。 输出格式: 输出 s s s…...

不同知识表示方法与知识图谱
目录 前言1 一阶谓词逻辑1.1 简介1.2 优势1.3 局限性 2 产生式规则2.1 简介2.2 优势2.3 局限性 3 框架系统3.1 简介3.2 优势3.3 局限性 4 描述逻辑4.1 简介4.2 优势4.3 局限性 5 语义网络5.1 简介5.2 优势5.3 局限性 结语 前言 知识表示是人工智能领域中至关重要的一环&#x…...

Kotlin程序设计 扩展篇(一)
Kotlin程序设计(扩展一) **注意:**开启本视频学习前,需要先完成以下内容的学习: 请先完成《Kotlin程序设计》视频教程。请先完成《JavaSE》视频教程。 Kotlin在设计时考虑到了与Java的互操作性,现有的Ja…...

星环科技基于第五代英特尔®至强®可扩展处理器的分布式向量数据库解决方案重磅发布
12月15日,2023 英特尔新品发布会暨 AI 技术创新派对上,星环科技基于第五代英特尔至强可扩展处理器的Transwarp Hippo分布式向量数据库解决方案重磅发布。该方案利用第五代英特尔至强可扩展处理器带来的强大算力,实现了约 2 倍的代际性能提升&…...

一体化运维的发展趋势与未来展望
随着信息技术的迅猛发展,企业的IT系统已经从单一的、孤立的应用转变为多元化、复杂化的系统集群。云计算、大数据、物联网等前沿技术的广泛应用,使得企业的IT运维面临着前所未有的挑战。在这样的背景下,一体化运维作为一种新型的运维模式&…...

科技云报道:金融大模型落地,还需跨越几重山?
科技云报道原创。 时至今日,大模型的狂欢盛宴仍在持续,而金融行业得益于数据密集且有强劲的数字化基础,从一众场景中脱颖而出。 越来越多的公司开始布局金融行业大模型,无论是乐信、奇富科技、度小满、蚂蚁这样的金融科技公司&a…...

C语言入门到精通之练习34:求100之内的素数
题目:求100之内的素数。 程序分析:质数(素数)酵母素数,有无限个。一个大于1的自然数,除了1和它本身外,不能被其他自然数整除。 代码如下: #include <stdio.h># #include &l…...

Qt采集本地摄像头推流成rtsp/rtmp(可网页播放/支持嵌入式linux)
一、功能特点 支持各种本地视频文件和网络视频文件。支持各种网络视频流,网络摄像头,协议包括rtsp、rtmp、http。支持将本地摄像头设备推流,可指定分辨率和帧率等。支持将本地桌面推流,可指定屏幕区域和帧率等。自动启动流媒体服…...

Oracle按日周月年自动分区
目录 1、分区键 2、初始分区 3、周月年自动分区 4、按日自动分区表建表语句 与普通建表语句相比,分区表多了一些分区信息; 1、分区键 以下面销售明细表为例,以data_dt为分区键,NUMTODSINTERVAL(1, day) 按日分区 PARTITION …...

单元测试、模块测试、web接口测试
单元测试与模块测试 什么是“单元测试”、“模块测试”? 然而在功能的实现代码中并没有“单元”,也没有“模块”;只有函数、类和方法。先来分别看看它们 的定义: 单元测试(Unit testing),是指…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
