22. 离线MC强化学习算法(1)
文章目录
- 1. 理解离线MC强化学习的关键
- 2. 什么是重要性采样
- 3.重要性采样定理给我们的一般启示
- 4.重要性采样定理给离线蒙特卡洛强化学习的启示
1. 理解离线MC强化学习的关键
离线强化学习的特点是采样策略 π ′ ≠ 待评估策略 π \pi'\ne 待评估策略\pi π′=待评估策略π,这就带来一个问题:
如何根据 π ′ \pi' π′获取的多条完整轨迹数据,计算得到 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)的估计值,而不是 Q π ′ ( s , a ) Q_{\pi'}(s,a) Qπ′(s,a)的估计值。
重要性采样定理为解决上述问题指明了方向,因此,理解重要性采样定理是理解离线MC强化学习的关键。
2. 什么是重要性采样
- 重要性采样定理的积分描述
已知随机变量 x x x的函数 f ( x ) f(x) f(x)、 x x x的两个不同概率分布 p ( x ) , q ( x ) p(x),q(x) p(x),q(x),令 g ( x ) = p ( x ) f ( x ) q ( x ) g(x)=\frac{p(x)f(x)}{q(x)} g(x)=q(x)p(x)f(x),设 E p ( f ) E_p(f) Ep(f)为 f ( x ) f(x) f(x)在 p ( x ) p(x) p(x)下的期望, E q ( g ) E_q(g) Eq(g)为 g ( x ) g(x) g(x)在 q ( x ) q(x) q(x)分布下的期望,则:
{ E p ( f ) = E q ( g ) E p ( f ) = ∫ x p ( x ) f ( x ) d x E q ( g ) = ∫ x q ( x ) g ( x ) d x \begin{align}\begin{cases} E_p(f)=E_q(g)\\ E_p(f)=\int_xp(x)f(x)dx\\ E_q(g)=\int_xq(x)g(x)dx \end{cases} \end{align} ⎩ ⎨ ⎧Ep(f)=Eq(g)Ep(f)=∫xp(x)f(x)dxEq(g)=∫xq(x)g(x)dx
- 重要性采样定理的统计学描述
根据重要性采样定理的积分描述,很容易推导出其统计学描述,如下:
已知对 x x x按照 q ( x ) q(x) q(x)进行采样得到的样本集为 S q = { x q , 1 , x q , 2 , ⋯ , x q , m } S_q=\{x_{q,1},x_{q,2},\cdots,x_{q,m}\} Sq={xq,1,xq,2,⋯,xq,m},则
可利用如下公式计算出 E p ( f ) E_p(f) Ep(f)的渐进无偏估计 E p ^ ( f ) \hat{E_p}(f) Ep^(f)和 E q ( g ) E_q(g) Eq(g)的
渐进无偏估计 E q ^ ( g ) \hat{E_q}(g) Eq^(g):
E p ^ ( f ) = E q ^ ( g ) = 1 m ∑ k = 1 m p ( x q , k ) f ( x q , k ) q ( x q , k ) \begin{align} \hat{E_p}(f)=\hat{E_q}(g)=\frac{1}{m}\sum_{k=1}^m\frac{p(x_{q,k})f(x_{q,k})}{q(x_{q,k})} \end{align} Ep^(f)=Eq^(g)=m1k=1∑mq(xq,k)p(xq,k)f(xq,k)
3.重要性采样定理给我们的一般启示
在估计 x x x的函数 f ( x ) f(x) f(x)在 p ( x ) p(x) p(x)下的期望时,若实际情形不允许按照 p ( x ) p(x) p(x)对 x x x进行采样,从而直接根据公式 E p ^ ( f ) = 1 m ∑ k = 1 m f ( x p , k ) \hat{E_p}(f)=\frac{1}{m}\sum_{k=1}^mf(x_{p,k}) Ep^(f)=m1∑k=1mf(xp,k)估计 E p ( f ) E_p(f) Ep(f)时,可以按照概率 q ( x ) q(x) q(x)
对 x x x进行采样获得样本集 S q S_q Sq,然后利用公式(2)进行间接估计,得到 E p ( f ) E_p(f) Ep(f)
4.重要性采样定理给离线蒙特卡洛强化学习的启示
在离线MC强化学习中,要解决的问题是:
已知采样策略 π ′ \pi' π′、待评估策略 π \pi π、利用 π ′ \pi' π′采集获得m条完整轨迹 E P = { E p 1 , E p 2 , ⋯ , E p m } EP=\{Ep_1,Ep_2,\cdots,Ep_m\} EP={Ep1,Ep2,⋯,Epm},其中, E p k = { ( s k , 0 , a k , 0 , r k , 1 ) , ( s k , 1 , a k , 1 , r k , 2 ) , ⋯ , ( s k , N k − 1 , a k , N k − 1 , r k , N k ) , ( s k , N k , a k , N k , r k , N k + 1 ) } , k = 1 , 2 , ⋯ , m Ep_k=\{(s_{k,0},a_{k,0},r_{k,1}),(s_{k,1},a_{k,1},r_{k,2}),\cdots,(s_{k,N_k-1},a_{k,N_k-1},r_{k,N_k}),(s_{k,N_k},a_{k,N_k},r_{k,N_k+1})\},k=1,2,\cdots,m Epk={(sk,0,ak,0,rk,1),(sk,1,ak,1,rk,2),⋯,(sk,Nk−1,ak,Nk−1,rk,Nk),(sk,Nk,ak,Nk,rk,Nk+1)},k=1,2,⋯,m,所有轨迹的
最后一个状态 s k , N k ≡ s T ( 终止状态 ) s_{k,N_k}\equiv s_T(终止状态) sk,Nk≡sT(终止状态)
,若固定 s t = s , a t = a s_t=s,a_t=a st=s,at=a,则每条轨迹中三元组 ( s , a , r ) (s,a,r) (s,a,r)中的 r r r可以看做是随机变量,累积回报 G π ′ ( s , a ) G^{\pi'}(s,a) Gπ′(s,a)是 r r r的函数
求解:策略 π \pi π下的累积回报函数 G π ( s , a ) G^{\pi}(s,a) Gπ(s,a)的期望 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)的估计值 Q π ^ ( s , a ) \hat{Q_\pi}(s,a) Qπ^(s,a)。
求解过程:
- 1.根据 E P EP EP,利用公式计算得到 ( s , a ) (s,a) (s,a)固定时,随机变量 r r r的函数 G π ′ ( s , a ) G^{\pi '}(s,a) Gπ′(s,a)在m个采样点
的样本函数值 G k π ′ ( s , a ) , k = 1 , 2 , ⋯ , m G^{\pi'}_k(s,a),k=1,2,\cdots,m Gkπ′(s,a),k=1,2,⋯,m - 2.根据重要性采样公式(2),及 G k π ′ ( s , a ) = G k π ( s , a ) G^{\pi '}_k(s,a)=G^{\pi}_k(s,a) Gkπ′(s,a)=Gkπ(s,a)可得:
Q π ^ ( s , a ) = 1 m ∑ k = 1 m p k π p k π ′ G k π ( s , a ) = 1 m ∑ k = 1 m p k π p k π ′ G k π ′ ( s , a ) p k π − 策略 π 下,出现完整轨迹 E p k 的概率 p k π ′ − 策略 π ′ 下,出现完整轨迹 E p k 的概率 ρ k = p k π p k π ′ − 重要性采样比例,表示待评估策略 π 下和采样策略 π ′ 下获得轨迹 E p k 的概率之比 p k π = [ π ( a k , 0 ∣ s k , 0 ) P s k , 0 s k , 1 a k , 0 ] × [ π ( a k , 1 ∣ s k , 1 ) P s k , 1 s k , 2 a k , 1 ] × ⋯ × [ π ( a k , N k − 1 ∣ s k , N k − 1 ) P s k , N k − 1 s k , N k a k , N k − 1 ] = ∏ i = 0 N k − 1 π ( a k , i ∣ s k , i ) P s k , i s k , i + 1 a k , i p k π ′ = ∏ i = 0 N k − 1 π ′ ( a k , i ∣ s k , i ) P s k , i s k , i + 1 a k , i ρ k = ∏ i = 0 N k − 1 π ( a k , i ∣ s k , i ) ∏ i = 0 N k − 1 π ′ ( a k , i ∣ s k , i ) \begin{align*} \hat{Q_\pi}(s,a)&=\frac{1}{m}\sum_{k=1}^m\frac{p_k^{\pi}}{p_k^{{\pi}'}}G^{{\pi}}_k(s,a)\\ &=\frac{1}{m}\sum_{k=1}^m\frac{p_k^{\pi}}{p_k^{{\pi}'}}G^{{\pi}'}_k(s,a)\\ p_k^{\pi}&-策略\pi 下,出现完整轨迹Ep_k的概率\\ p_k^{\pi'}&-策略\pi' 下,出现完整轨迹Ep_k的概率\\ \rho_k=\frac{p_k^{\pi}}{p_k^{\pi'}}&-重要性采样比例,表示待评估策略\pi 下和采样策略\pi' 下获得轨迹Ep_k的概率之比\\ p_k^{\pi}&=[\pi(a_{k,0}|s_{k,0})P_{s_{k,0}s_{k,1}}^{a_{k,0}}]\times [\pi(a_{k,1}|s_{k,1})P_{s_{k,1}s_{k,2}}^{a_{k,1}}]\times\cdots \times[\pi(a_{k,N_k-1}|s_{k,N_k-1})P_{s_{k,N_k-1}s_{k,N_k}}^{a_{k,N_k-1}}]\\ &=\prod_{i=0}^{N_k-1}\pi(a_{k,i}|s_{k,i})P_{s_{k,i}s_{k,i+1}}^{a_{k,i}}\\ p_k^{\pi'}&=\prod_{i=0}^{N_k-1}\pi'(a_{k,i}|s_{k,i})P_{s_{k,i}s_{k,i+1}}^{a_{k,i}}\\ \rho_k&=\frac{\prod_{i=0}^{N_k-1}\pi(a_{k,i}|s_{k,i})}{\prod_{i=0}^{N_k-1}\pi'(a_{k,i}|s_{k,i})} \end{align*} Qπ^(s,a)pkπpkπ′ρk=pkπ′pkπpkπpkπ′ρk=m1k=1∑mpkπ′pkπGkπ(s,a)=m1k=1∑mpkπ′pkπGkπ′(s,a)−策略π下,出现完整轨迹Epk的概率−策略π′下,出现完整轨迹Epk的概率−重要性采样比例,表示待评估策略π下和采样策略π′下获得轨迹Epk的概率之比=[π(ak,0∣sk,0)Psk,0sk,1ak,0]×[π(ak,1∣sk,1)Psk,1sk,2ak,1]×⋯×[π(ak,Nk−1∣sk,Nk−1)Psk,Nk−1sk,Nkak,Nk−1]=i=0∏Nk−1π(ak,i∣sk,i)Psk,isk,i+1ak,i=i=0∏Nk−1π′(ak,i∣sk,i)Psk,isk,i+1ak,i=∏i=0Nk−1π′(ak,i∣sk,i)∏i=0Nk−1π(ak,i∣sk,i)
相关文章:
)
22. 离线MC强化学习算法(1)
文章目录 1. 理解离线MC强化学习的关键2. 什么是重要性采样3.重要性采样定理给我们的一般启示4.重要性采样定理给离线蒙特卡洛强化学习的启示 1. 理解离线MC强化学习的关键 离线强化学习的特点是采样策略 π ′ ≠ 待评估策略 π \pi\ne 待评估策略\pi π′待评估策略π&…...

如何阅读xml电子发票
xml电子发票是官方给出的电子存档的文件格式,本质是文本,所以文件很小,大量发票存储,能够更加凸显优势。 但是xml电子发票不方便阅读,因为里面是xml格式,对于财务人员来讲,看“代码”简直太难了…...

php实现多进程的几种方式
目录 一:使用pcntl扩展库 二:使用Swoole扩展 三:使用多进程模式PHP-FPM 在PHP中实现多进程主要有以下几种方式: 一:使用pcntl扩展库 pcntl扩展库提供了多线程相关的函数,如pcntl_fork()用于创建子进程…...
CmakeList教程
一、CmakeList介绍: cmake 是一个跨平台、开源的构建系统。它是一个集软件构建、测试、打包于一身的软件。它使用与平台和编译器独立的配置文件来对软件编译过程进行控制。它会通过写的语句自动生成一个MakeFile,从而实现高效编译 二、CmakeList的常用指令 1.指定…...
JavaWeb之JavaScript-Vue --黑马笔记
什么是JavaScript? JavaScript(简称:JS) 是一门跨平台、面向对象的脚本语言。是用来控制网页行为的,它能使网页可交互。 JavaScript 和 Java 是完全不同的语言,不论是概念还是设计。但是基础语法类似。 …...
pikachu_ssrf攻略
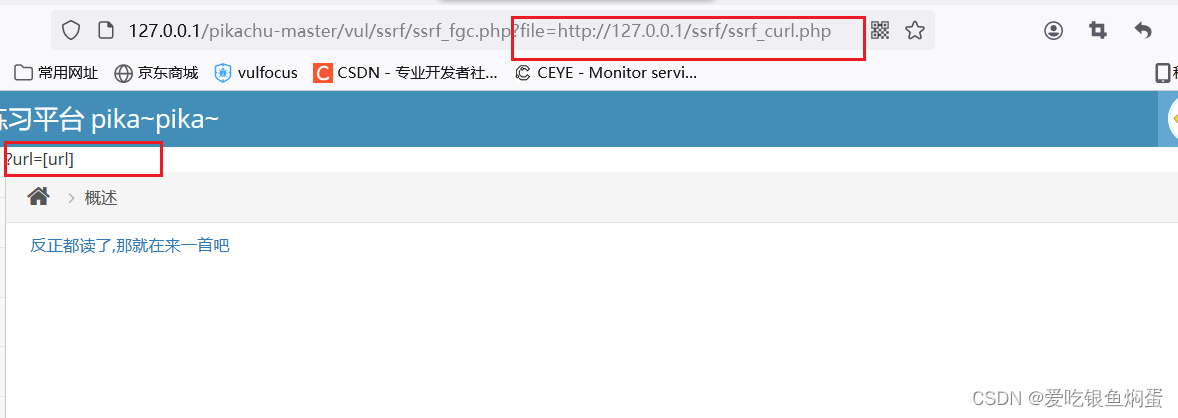
ssrf(curl): 打开pikachu靶场: http://127.0.0.1/pikachu-master/vul/ssrf/ssrf_curl.php?urlhttp://127.0.0.1/pikachu-master/vul/ssrf/ssrf_info/info1.php 发现URL地址最后面是info1.php 猜测一下有没有可能存在info2.php?…...

门面模式 Facade Pattern
门面模式 门面模式(Facade Pattern),也称之为外观模式,其核心为:外部与一个子系统的通信必须通过一个统一的外观对象进行,使得子系统更易于使用。 在软件开发领域有这样一句话:计算机科学领域…...

Linux基础指令大汇总
Linux的指令比较多,在学习的过程中要学会总结和归纳,同时结合实践多多使用,就像学数学一样,不是背过公式就等于掌握的,而是要知道在什么时候用,怎么用才是关键。 这篇文章会列举一系列常用的指令࿰…...
Unity配置表xlsx/xls打包后读取错误问题
前言 代码如下: //文本解析private void ParseText(){//打开文本 读FileStream stream File.Open(Application.streamingAssetsPath excelname, FileMode.Open, FileAccess.Read, FileShare.Read);//读取文件流IExcelDataReader excelRead ExcelReaderFactory…...

CSS基本知识总结
目录 一、CSS语法 二、CSS选择器 三、CSS样式表 1.外部样式表 2.内部样式表 3.内联样式 四、CSS背景 1.背景颜色:background-color 2.背景图片:background-image 3.背景大小:background-size 4.背景图片是否重复:backg…...
3dmax效果图渲染出现曝光怎么解决?
在使用3ds Max完成效果图渲染工作时,有时会遇到曝光过度的问题,这会使得渲染的图像出现光斑或者过亮,损害了效果的真实感和美观度。那么解决解决3dmax曝光问题呢?一起看看吧! 3dmax效果图渲染出现曝光解决方法 1、相机…...
科技、文化与旅游的融合创新:智慧文旅的未来之路
在当今社会,科技、文化与旅游的融合已经成为文旅产业转型升级的重要趋势。这种融合不仅有助于提升文旅产业的核心竞争力,更有助于推动产业的数字化转型和可持续发展。 本文将深入探讨科技、文化与旅游的融合创新,以及智慧文旅场景的解决方案…...

【第四天】蓝桥杯备战
题 1、求和2、天数3、最大缝隙 1、求和 https://www.lanqiao.cn/problems/1442/learning/ 解法:字符串方法的应用 import java.util.Scanner; // 1:无需package // 2: 类名必须Main, 不可修改public class Main {public static void main(String[] args) {Scann…...

计算机服务器中了halo勒索病毒怎么办,halo勒索病毒解密处理流程
计算机技术的发展与应用为企业的生产生活提供了坚实基础,但同时也为网络安全威胁制造了有利条件。近期,网络上的勒索病毒非常嚣张,给企业的计算机服务器带来严重威胁。近日,云天数据恢复中心接到山东某制造公司的求助,…...

基于LSTM的负荷预测,基于BILSTM的负荷预测,基于GRU的负荷预测,基于BIGRU的负荷预测,基于BP神经网络的负荷预测
目录 背影 摘要 代码和数据下载:基于LSTM的负荷预测,基于BILSTM的负荷预测,基于GRU的负荷预测,基于BIGRU的负荷预测,基于BP神经网络的负荷预测资源-CSDN文库 https://download.csdn.net/download/abc991835105/8876806…...
)
Linux命令-apachectl命令(Apache服务器前端控制工具)
apachectl命令 是Apache的Web服务器前端控制工具,用以启动、关闭和重新启动Web服务器进程。 语法 apachectl (参数)参数 configtest:检查设置文件中的语法是否正确;fullstatus:显示服务器完整的状态信息;graceful&a…...

5.【SpringBoot3】文件上传
1. 文件上传到本地 需求分析 在用户更换头像或发布文章时,需要携带一个图片的 url 地址,该 url 地址是当用户访问文件上传接口,将图片上传成功后,服务器返回的地址。所以,后台需要提供一个文件上传接口,用…...

网络安全态势感知平台概述
网络安全态势感知平台 文章目录 网络安全态势感知平台网络安全态势感知平台是什么一、网络安全态势感知平台是什么?二、网络安全态势感知很重要三、网络安全态势感知基础功能以某公司态势平台产品为例具体功能有以下: 网络安全态势感知平台是什么 网络安…...
)
PHP导出csv文件格式(最快捷的方式导出Excel文件)
php导出csv文件格式比起用PHPExcel插件导出excel文件速度快100倍! 以下是几种不同的PHP导出CSV文件的方法: 方法一(php://output方式用fputcsv函数格式化成csv数据): ----------------------------------------------…...

vue3常用代码
文章目录 监听路由vue3 警告Feature flag __VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.mitt、project/inject 无效解决方案 菜鸟做项目时发现很多 vue3 常用的代码,所以来总结一下! 监听路由 import { useRoute } from "…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
