C#,打印漂亮杨辉三角形(帕斯卡三角形)的源代码

杨辉

Blaise Pascal
这是某些程序员看完会哭的代码。
杨辉三角形(Yanghui Triangle),是一种序列数值的三角形几何排列,最早出现于南宋·数学家·杨辉1261年所著的《详解九章算法》一书。
欧洲学者,最先由帕斯卡(1623----1662)在1654年发现这一规律,故杨辉三角又称“帕斯卡三角形(Pascal Truangle)”。

图中暖色为偶数;冷色为奇数。
代码1:
private void button1_Click(object sender, EventArgs e)
{
webBrowser1.DocumentText = Magic_Numbers.YangHui_Triangle(20);
}
private void button1_Click(object sender, EventArgs e)
{webBrowser1.DocumentText = Magic_Numbers.YangHui_Triangle(20);
}代码2:
using System;
using System.Text;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Magic_Numbers
{
public static string YangHui_Triangle(int n)
{
StringBuilder sb = new StringBuilder();
sb.AppendLine("<style>");
sb.AppendLine(".n0 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #993333;background-color:#FFF9F9;margin-right:10px;margin-bottom:10px; } ");
sb.AppendLine(".n1 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #333399;background-color:#F9F9FF;margin-right:10px;margin-bottom:10px; } ");
sb.AppendLine("</style>");
sb.AppendLine("<center>");
long[] last = new long[n];
last[0] = 1;
for (int i = 1; i <= n; i++)
{
sb.AppendLine("<table><tr><td>");
long[] array = new long[i];
array[0] = 1;
sb.AppendLine("<div class='n"+ (array[0]%2) +"'>" + array[0] + "</div>");
for (int j = 1; j < i; j++)
{
array[j] = last[j - 1] + last[j];
sb.AppendLine("<div class='n" + (array[j] % 2) + "'>" + array[j] + "</div>");
}
for (int j = 0; j < i; j++)
{
last[j] = array[j];
}
sb.AppendLine("</td></tr></table>");
}
return sb.ToString();
}
}
}
using System;
using System.Text;namespace Legalsoft.Truffer.Algorithm
{public static partial class Magic_Numbers{public static string YangHui_Triangle(int n){StringBuilder sb = new StringBuilder();sb.AppendLine("<style>");sb.AppendLine(".n0 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #993333;background-color:#FFF9F9;margin-right:10px;margin-bottom:10px; } ");sb.AppendLine(".n1 { float:left;width:90px;height:25px;line-height:25px;font-size:14px;text-align:center;border:dotted 1px #333399;background-color:#F9F9FF;margin-right:10px;margin-bottom:10px; } ");sb.AppendLine("</style>");sb.AppendLine("<center>");long[] last = new long[n];last[0] = 1;for (int i = 1; i <= n; i++){sb.AppendLine("<table><tr><td>");long[] array = new long[i];array[0] = 1;sb.AppendLine("<div class='n"+ (array[0]%2) +"'>" + array[0] + "</div>");for (int j = 1; j < i; j++){array[j] = last[j - 1] + last[j];sb.AppendLine("<div class='n" + (array[j] % 2) + "'>" + array[j] + "</div>");}for (int j = 0; j < i; j++){last[j] = array[j];}sb.AppendLine("</td></tr></table>");}return sb.ToString();}}
}相关文章:

C#,打印漂亮杨辉三角形(帕斯卡三角形)的源代码
杨辉 Blaise Pascal 这是某些程序员看完会哭的代码。 杨辉三角形(Yanghui Triangle),是一种序列数值的三角形几何排列,最早出现于南宋数学家杨辉1261年所著的《详解九章算法》一书。 欧洲学者,最先由帕斯卡&#x…...
[SUCTF 2019]CheckIn1
黑名单过滤后缀’ph,并且白名单image类型要有对应文件头 对<?过滤,改用GIF89a<script languagephp>eval($_POST[cmd]);</script>,成功把getshell.gif上传上去了 尝试用.htaccess将上传的gif当作php解析,但是失败…...

C语言练习题110例(十)
91.杨辉三角 题目描述: KK知道什么叫杨辉三角之后对杨辉三角产生了浓厚的兴趣,他想知道杨辉三角的前n行,请编程帮他 解答。杨辉三角,本质上是二项式(ab)的n次方展开后各项的系数排成的三角形。其性质包括:每行的端点数为1&…...

前端学习-0125
<h>标签 含义:标题 级别:<h1> - <h6> 快捷键生成 :h$*[0,6] 属性:align"left|center|right" <p>标签 含义: 段落 <br>标签 含义:换行 <hr>标签 含义&…...

gin中使用validator做参数校验
在web开发中对请求参数进行校验,通常在代码中定义与请求参数相对应的模型(结构体),借助模型绑定快捷地解析请求中的参数,例如 gin 框架中的Bind和ShouldBind系列方法。 gin框架使用github.com/go-playground/validato…...
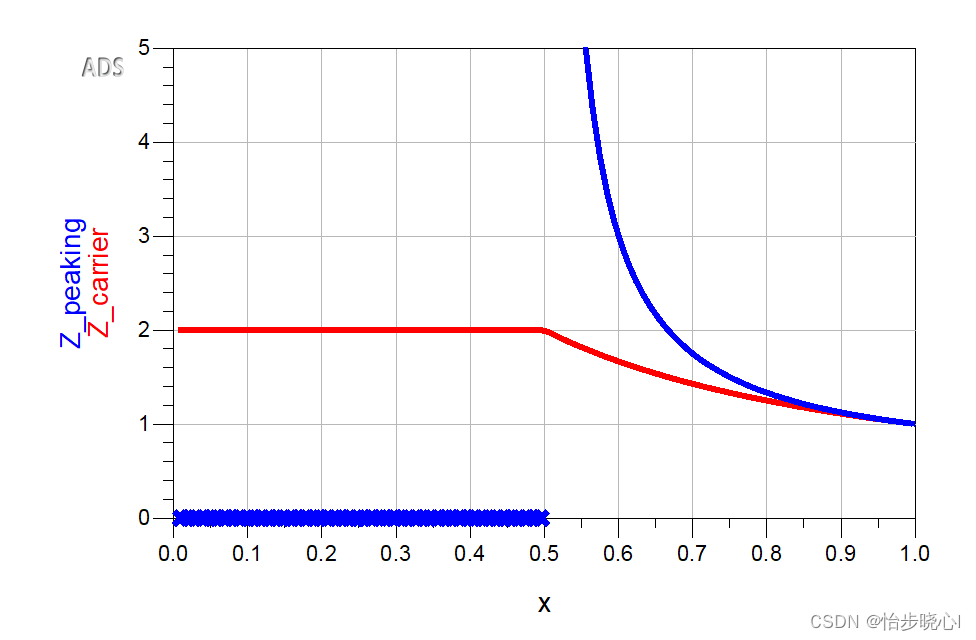
理想架构的Doherty功率放大器理论与仿真
Doherty理论—理想架构的Doherty功率放大器理论与仿真 参考: 三路Doherty设计 01 射频基础知识–基础概念 ADS仿真工程文件链接:理想架构的Doherty功率放大器理论与仿真 目录 Doherty理论---理想架构的Doherty功率放大器理论与仿真0、Doherty架构的作用…...
)
22. 离线MC强化学习算法(1)
文章目录 1. 理解离线MC强化学习的关键2. 什么是重要性采样3.重要性采样定理给我们的一般启示4.重要性采样定理给离线蒙特卡洛强化学习的启示 1. 理解离线MC强化学习的关键 离线强化学习的特点是采样策略 π ′ ≠ 待评估策略 π \pi\ne 待评估策略\pi π′待评估策略π&…...

如何阅读xml电子发票
xml电子发票是官方给出的电子存档的文件格式,本质是文本,所以文件很小,大量发票存储,能够更加凸显优势。 但是xml电子发票不方便阅读,因为里面是xml格式,对于财务人员来讲,看“代码”简直太难了…...

php实现多进程的几种方式
目录 一:使用pcntl扩展库 二:使用Swoole扩展 三:使用多进程模式PHP-FPM 在PHP中实现多进程主要有以下几种方式: 一:使用pcntl扩展库 pcntl扩展库提供了多线程相关的函数,如pcntl_fork()用于创建子进程…...
CmakeList教程
一、CmakeList介绍: cmake 是一个跨平台、开源的构建系统。它是一个集软件构建、测试、打包于一身的软件。它使用与平台和编译器独立的配置文件来对软件编译过程进行控制。它会通过写的语句自动生成一个MakeFile,从而实现高效编译 二、CmakeList的常用指令 1.指定…...
JavaWeb之JavaScript-Vue --黑马笔记
什么是JavaScript? JavaScript(简称:JS) 是一门跨平台、面向对象的脚本语言。是用来控制网页行为的,它能使网页可交互。 JavaScript 和 Java 是完全不同的语言,不论是概念还是设计。但是基础语法类似。 …...
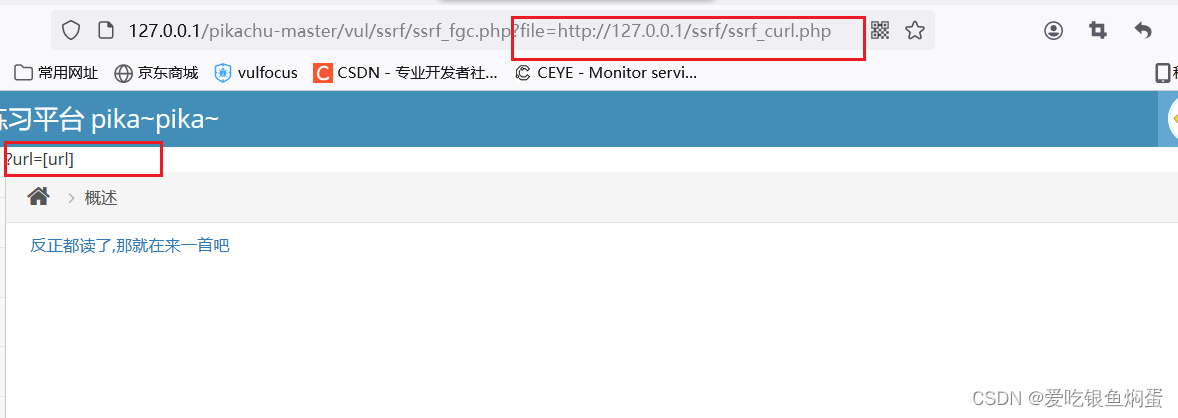
pikachu_ssrf攻略
ssrf(curl): 打开pikachu靶场: http://127.0.0.1/pikachu-master/vul/ssrf/ssrf_curl.php?urlhttp://127.0.0.1/pikachu-master/vul/ssrf/ssrf_info/info1.php 发现URL地址最后面是info1.php 猜测一下有没有可能存在info2.php?…...

门面模式 Facade Pattern
门面模式 门面模式(Facade Pattern),也称之为外观模式,其核心为:外部与一个子系统的通信必须通过一个统一的外观对象进行,使得子系统更易于使用。 在软件开发领域有这样一句话:计算机科学领域…...

Linux基础指令大汇总
Linux的指令比较多,在学习的过程中要学会总结和归纳,同时结合实践多多使用,就像学数学一样,不是背过公式就等于掌握的,而是要知道在什么时候用,怎么用才是关键。 这篇文章会列举一系列常用的指令࿰…...
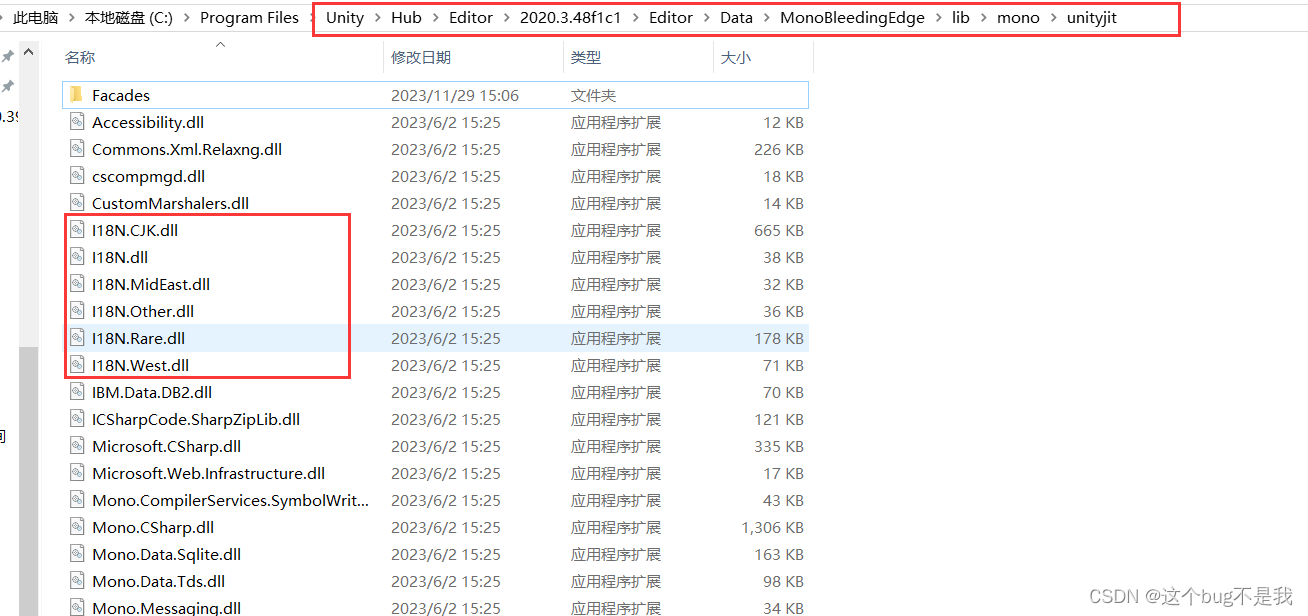
Unity配置表xlsx/xls打包后读取错误问题
前言 代码如下: //文本解析private void ParseText(){//打开文本 读FileStream stream File.Open(Application.streamingAssetsPath excelname, FileMode.Open, FileAccess.Read, FileShare.Read);//读取文件流IExcelDataReader excelRead ExcelReaderFactory…...

CSS基本知识总结
目录 一、CSS语法 二、CSS选择器 三、CSS样式表 1.外部样式表 2.内部样式表 3.内联样式 四、CSS背景 1.背景颜色:background-color 2.背景图片:background-image 3.背景大小:background-size 4.背景图片是否重复:backg…...
3dmax效果图渲染出现曝光怎么解决?
在使用3ds Max完成效果图渲染工作时,有时会遇到曝光过度的问题,这会使得渲染的图像出现光斑或者过亮,损害了效果的真实感和美观度。那么解决解决3dmax曝光问题呢?一起看看吧! 3dmax效果图渲染出现曝光解决方法 1、相机…...
科技、文化与旅游的融合创新:智慧文旅的未来之路
在当今社会,科技、文化与旅游的融合已经成为文旅产业转型升级的重要趋势。这种融合不仅有助于提升文旅产业的核心竞争力,更有助于推动产业的数字化转型和可持续发展。 本文将深入探讨科技、文化与旅游的融合创新,以及智慧文旅场景的解决方案…...

【第四天】蓝桥杯备战
题 1、求和2、天数3、最大缝隙 1、求和 https://www.lanqiao.cn/problems/1442/learning/ 解法:字符串方法的应用 import java.util.Scanner; // 1:无需package // 2: 类名必须Main, 不可修改public class Main {public static void main(String[] args) {Scann…...

计算机服务器中了halo勒索病毒怎么办,halo勒索病毒解密处理流程
计算机技术的发展与应用为企业的生产生活提供了坚实基础,但同时也为网络安全威胁制造了有利条件。近期,网络上的勒索病毒非常嚣张,给企业的计算机服务器带来严重威胁。近日,云天数据恢复中心接到山东某制造公司的求助,…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
