【新书推荐】2.6节 原码、反码和补码
回顾上一节中,我们讲解了整数的编码规则。
无符号整数编码规则:无符号整数全部都是正数,是什么就存什么。
有符号整数编码规则:有符号整数最高有效位为0是正数,最高有效位为1是负数。
本节内容:原码、反码和补码。
■为什么要有原码、反码和补码:8086 CPU只有加法电路,通过加法电路实现减法、乘法和除法运算。将减法转换为加法运算需要将负数转换为补码,如1-2=1+(-2),-2以其补码形式存储。因此,只有负整数存在原码、反码和补码。
■原码、反码、补码的定义:原码——最高位为符号位,其余各位为数值本身的绝对值。反码——符号位不变,其余各位取反。补码——符号位不变,其余各位取反后加1。
■原码、反码、补码的转换规则:首先指定数据宽度,然后按照定义的规则进行转换。记住圆形数据范围内,左半圆为负整数,右半圆为正整数。
2.6.1 为什么要有原码、反码、补码
由于早期的8086 CPU只支持加法指令,减法、乘法和除法都是通过加法指令实现的。例如:减法运算2-3=?等价于加法运算2+(-3)=?那么剩下的问题就是如何在计算机内存储有符号整数值“-3”。这就需要用到原码、反码和补码的编码规则了。
注意
当算术运算表达式中的两个整数都是无符号整数或者有符号整数的正整数时,不存在减法转加法运算的问题。即原码、反码和补码仅针对于有符号整数的负整数。
再次强调,数据定义一定要指明数据的宽度。
2.6.2 原码、反码、补码的定义
■原码:最高位为符号位,(“0”代表正数,“1”代表负数)其余各位为数值本身的绝对值。
■反码:
正数:反码与原码相同,这是规定。
负数:符号位为1不变,其余位对原码取反。
■补码:
正数:补码与原码相同。
负数:符号位为1不变,其余位对原码取反加1。
举例
例1:写出有符号整数1(8位数据宽度)的原码、反码、补码。
原码:0000 0001 反码:0000 0001 补码:0000 0001
例2:写出有符号整数-1(8位数据宽度)的原码、反码、补码。
原码:1000 0001 反码:1111 1110 补码:1111 1111=>FF
例3:写出有符号整数-7(8位数据宽度)的原码、反码、补码。
原码:1000 0111 反码:1111 1000 补码:1111 1001=>F9
例4:写出有符号整数F9(8位数据宽度)的原码、反码、补码。
原码:1111 1001 反码:1000 0110 补码:1000 0111=>-7
例3和例4,-7的补码是F9,F9的补码是-7,即补码的补码等于自身。
2.6.3 原码、反码和补码的转换规则
■假设数据宽度为1 BYTE(8 BIT)
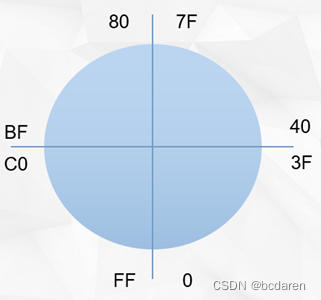
图2-22 BYTE数据类型存储范围
如图2-22所示:
无符号数:0 1 2 3 4 ......FF
有符号数:
正数:0 .......7F
负数:FF ........80
■假设数据宽度为Doubleword(32BIT)

图2-23 Dword数据类型存储范围
如图2-23所示:
无符号数:0 1 2 3 4 ......FFFFFFFF
有符号数:
正数:0 .......7FFFFFFF
负数:FFFFFFFF ........80000000
■有符号数的编码规则
如果是正数,不变。
如果是负数,分析图2-24所示左右两个半圆部分。
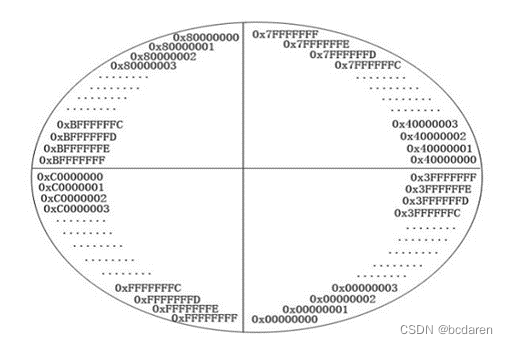
图2-24 32位整数数据范围
分析图2-24有符号整数:
| 第8位 | 第7位 | 第6位 | 第5位 | 第4位 | 第3位 | 第2位 | 第1位 | |
| 0XBFFFFFFF | 1011 | 1111 | 1111 | 1111 | 1111 | 1111 | 1111 | 1111 |
| 0X40000000 | 0100 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
表2-9 反码对照表
表2-9中举例说明:圆的左右两边对应的整数互为反码。
■补码为什么要+1

表2-10 4位有符号数-1~-8原码反码补码
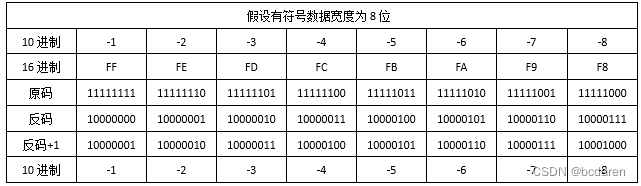
表2-11 8位有符号数-1~-8原码反码补码
注意:最高位符号位不参与运算。
表2-10和表2-11分别展示了4位和8位-1~-8的原码、反码和补码的推导过程。符号位不参与运算,保持不变。反码+1后与原码的表示有符号整数值相同。
举例
假设数据宽度为8位。
有符号数-1的补码为:11111111B。
有符号数-3的补码为:11111101B。
1-1=1+(-1)=[00000001B]+[11111111B]=[00000000B]=0发生进位后,数据溢出,舍弃。
5-3=5+(-3)=[00000101B]+[11111101B]=[00000010B]=2。
总结
1.正整数不存在原码、反码和补码的转换,是什么就存什么。
2.只有负整数存在原码、反码和补码的转换。
3.负整数以补码形式存储到内存中,由编译器实现原码、反码和补码的转换。
4.最高位符号位1不参与取反,也不参与有符号数的算术逻辑运算。
练习
1、为什么要有数据宽度?
2、已知0x9A是一个有符号数,那么请说明它是正数还是负数?
3、分别列出 6、-6、7、-7、8、-8、9、-9、1、-1、0、-0 的原码反码补码。
4、已知数据宽度为8Bit,请通过下面的值得到对应原码:
7F 9A 86 5F 3E A3 B7 5D
5、已知数据宽度为32 Bit,请通过下面的值得到对应原码:
0xFFFFFF 0x81234567
6、有符号的正数是原码存储,有符号的负数是补码存储,那么无符号数呢?
7、当计算机中存储的0x81234时,代表的值是多少?
8、假设有符号数数据宽度为8位,其取值范围是-128~127,请问为何负整数取值比正整数多一个值?
本文摘自编程达人系列教材《X86汇编语言基础教程》。
相关文章:

【新书推荐】2.6节 原码、反码和补码
回顾上一节中,我们讲解了整数的编码规则。 无符号整数编码规则:无符号整数全部都是正数,是什么就存什么。 有符号整数编码规则:有符号整数最高有效位为0是正数,最高有效位为1是负数。 本节内容:原码、反…...
docker 网络及如何资源(CPU/内存/磁盘)控制
安装Docker时,它会自动创建三个网络,bridge(创建容器默认连接到此网络)、 none 、host docker网络模式 Host 容器与宿主机共享网络namespace,即容器和宿主机使用同一个IP、端口范围(容器与宿主机或其他使…...
安装 nvm
前言: nvm 即 node 版本管理工具 (node version manager),好处是方便切换 node.js 版本。 通过将多个 node 版本安装在指定路径,然后通过 nvm 命令切换时,就会切换我们环境变量中 node 命令指定的实际执行的软件路径。 使用场景…...

Redis解决方案:NOAUTH Authentication required(连接jedis绑定密码或修改redis密码)
Redis解决方案:NOAUTH Authentication required(连接jedis绑定密码或修改redis密码) Java使用jedis连接redis时出现错误NOAUTH Authentication required 一、问题报错和原因 本地设置了redis的密码,但在远程连接时并没有输入密…...

多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测
多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测 目录 多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测效果一览基本介绍程序设计参考资料 效…...

如何实现无公网IP实现远程访问MongoDB文件数据库
📑前言 本文主要是如何实现无公网IP实现远程访问MongoDB文件数据库的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 &#x…...
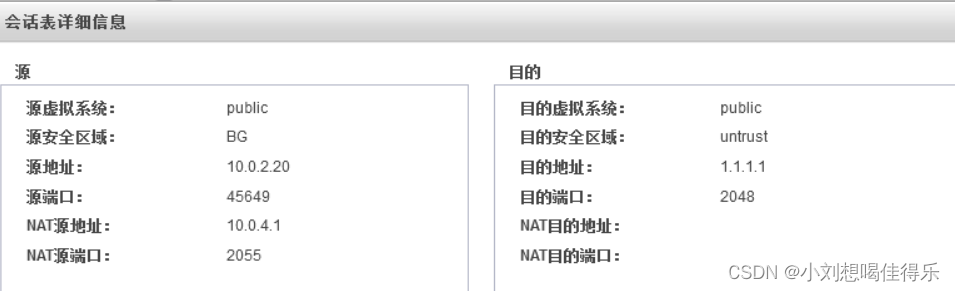
华为防火墙USG6000V1的NAT实验
实验拓扑: 之前实验做过,可以翻找之前的博客,各设备ip和接口已配好,均可可ping通防火墙。 实验要求: 一.生产区在工作时间内可以访问dmz区域,仅可以访问http服务器。 二.办公区全天可以访问dmz区域&…...

spark-flink设计思想之吸星大法-1
Spark和Flink都是大数据处理框架,它们的设计思想有一些不同之处。以下是对它们设计思想的简要对比: 数据模型和计算模型: Spark:Spark使用弹性分布式数据集(RDD)作为其核心数据结构。RDD是只读的、不可变的…...

力扣1312. 让字符串成为回文串的最少插入次数
动态规划 思路: 通过插入字符构造回文串,要想插入次数最少,可以将字符串 s 的逆序 s 进行比较找出最长公共子序列;可以先分析,字符串 s 通过插入得到回文串 ps,其中间的字符应该不会变化: 若 s…...
qemu的安装
1、简介 QEMU(Quick EMUlator)是一个开源的处理器模拟器,它可以在一种硬件平台上模拟另一种硬件平台,从而运行各种不同的操作系统。QEMU通过动态二进制翻译来实现高性能的模拟,这使得它可以在接近原生性能的速度下运行…...

myql入门
目录 安装修改密码学习资料个人git仓库文章视频官网 安装 #移除以前的mysql相关 sudo apt remove --purge mysql-\* #安装mysql sudo apt install mysql-server mysql-client #查看是否启动 systemctl status mysql #手动启动 systemctl start mysql #查看mysql版本 mysql --v…...

前端开发有没有必要转鸿蒙开发?
前端开发有没有必要转鸿蒙开发?如果后面的工作中有参与鸿蒙开发的机会,那肯定是转呀!毕竟多接触一些技能也不会有什么坏处。 我想说的是:鸿蒙替代不了前端,如果你目前正在从事前端开发,那么你完全可以将鸿蒙…...
》笔记1)
《动手学深度学习(PyTorch版)》笔记1
Chapter1 Introduction 1.1 机器学习的关键组件 data 每个数据集由一个个样本(example, sample)组成,大多时候,它们遵循独立同分布(independently and identically distributed, i.i.d.)。 样本有时也叫做数据点(dat…...
)
前端工程化之:webpack1-5(配置文件)
一、配置文件 webpack 提供的 cli 支持很多的参数,例如 --mode ,但更多的时候,我们会使用更加灵活的配置文件来控制 webpack 的行为。 默认情况下, webpack 会读取 webpack.config.js 文件作为配置文件,但也可以通过 C…...

代码随想录栈和队列专题二刷复盘day17
栈和队列理论基础 队列是先进先出,栈是先进后出 栈和队列是STL里面的两个数据结构 三个最为普遍的STL版本 1.HP STL其他版本的C STL,一般是以HP STL为蓝本实现出来的,HP STL是C STL的第一个实现版本,且开放源代码 2.P.J.Plauger…...
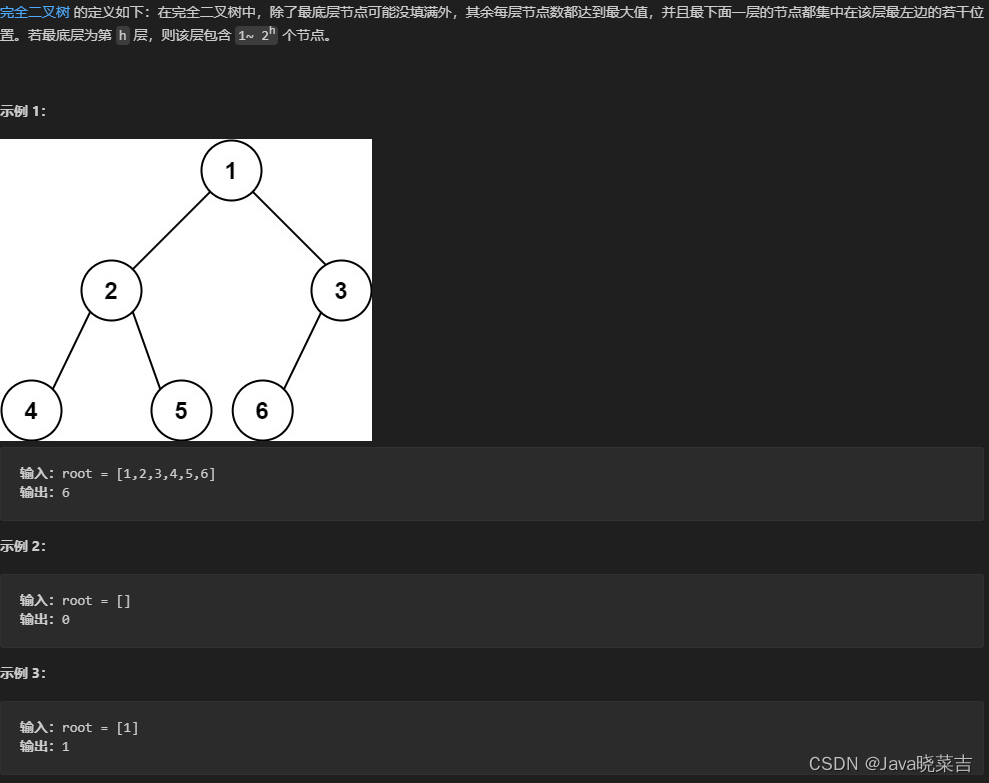
代码随想录算法刷题训练营day16
代码随想录算法刷题训练营day16:LeetCode(104)二叉树的最大深度 、LeetCode(559)n叉树的最大深度、LeetCode(111)二叉树的最小深度、LeetCode(222)完全二叉树的节点个数 LeetCode(104)二叉树的最大深度 题目 代码 /*** Definition for a binary tree node.* publ…...

【C语言/数据结构】排序(直接插入排序|希尔排序)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm1001.2014.3001.5482 目录 插入排序 直接插入排序&…...
Jupyter Notebook安装使用教程
Jupyter Notebook 是一个基于网页的交互式计算环境,允许你创建和共享包含代码、文本说明、图表和可视化结果的文档。它支持多种编程语言,包括 Python、R、Julia 等。其应用场景非常广泛,特别适用于数据科学、机器学习和教育领域。它可以用于数…...

Unity 中的接口和继承
在Unity的游戏开发中,理解面向对象编程的概念,如类、接口、继承和多态性,是非常重要的。本文旨在帮助理解和掌握Unity中接口和继承的概念,以及如何在实际项目中应用这些知识。 类和继承 在C#和Unity中,类是构建应用程序…...
)
C++区间覆盖(贪心算法)
假设有n个区间,分别是:[l1,r1], [l2,r2], [l3,r3].....[ln,rn] 从这n个区间中选出某些区间,要求这些区间满足两两不相交,最多能选出多少个区间呢? 基本思路: 按照右端点从小到大排序,再比较左端…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...
