机器学习实验3——支持向量机分类鸢尾花
文章目录
- 🧡🧡实验内容🧡🧡
- 🧡🧡数据预处理🧡🧡
- 代码
- 认识数据
- 相关性分析
- 径向可视化
- 各个特征之间的关系图
- 🧡🧡支持向量机SVM求解🧡🧡
- 直觉理解:
- 数学推导
- 代码
- 运行结果
- 🧡🧡总结🧡🧡
🧡🧡实验内容🧡🧡
基于鸢尾花数据集,完成关于支持向量机的分类模型训练、测试与评估。
🧡🧡数据预处理🧡🧡
代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler# ==================特征探索====================# ===认识数据===
iris = datasets.load_iris()
print("Feature names: {}".format(iris['feature_names']))
print("Target names: {}".format(iris["target_names"]))
print("target:\n{}".format(iris['target'])) # 0 代表setosa,1 代表versicolor,2 代表virginica。
print("shape of data: {}".format(iris['data'].shape))# ===转为df对象===
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
feature_df=df.drop('label',axis=1,inplace=False) # 取出特征
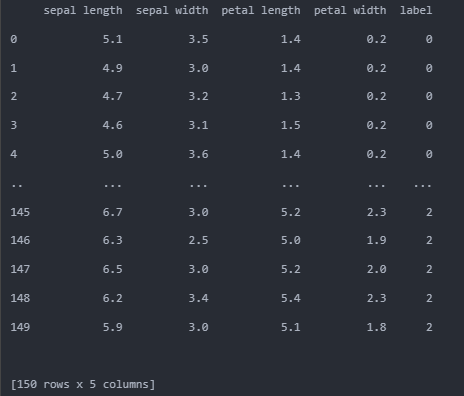
print(df)# ===相关性矩阵===
corr_matrix = feature_df.corr()
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()# ===径向可视化===
ax = pd.plotting.radviz(df, 'label', colormap='brg')
ax.add_artist(plt.Circle((0,0), 1, color='r', fill = False))# ===各特征之间关系矩阵图===
# 设置颜色主题
g = sns.pairplot(data=df, palette="pastel", hue= 'label')
认识数据
属性:花萼长度,花萼宽度,花瓣长度,花瓣宽度
分类:Setosa,Versicolour,Virginica
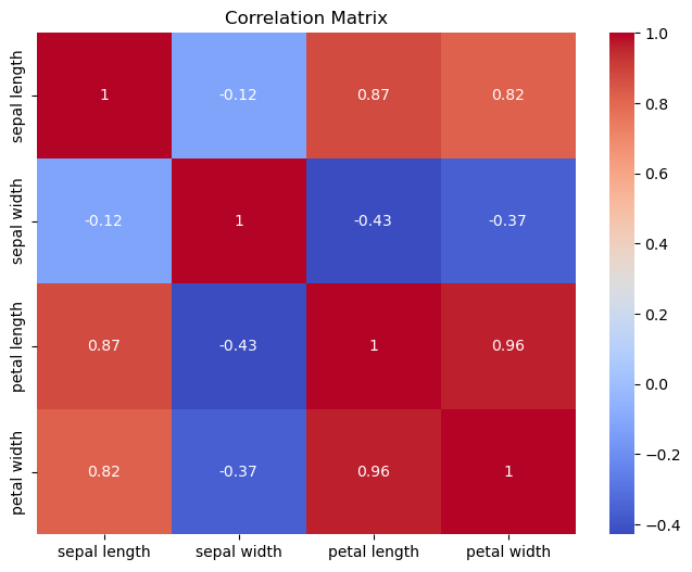
相关性分析
如下图,可以直观看到花瓣宽度(Petal Width)和花瓣长度(Petal Length)存在很高的正相关性,且它们与花萼长度(Speal Length)也具有很高的正相关性,而花萼宽度(Speal Width)与其他三个属性特征的相关性均很弱。
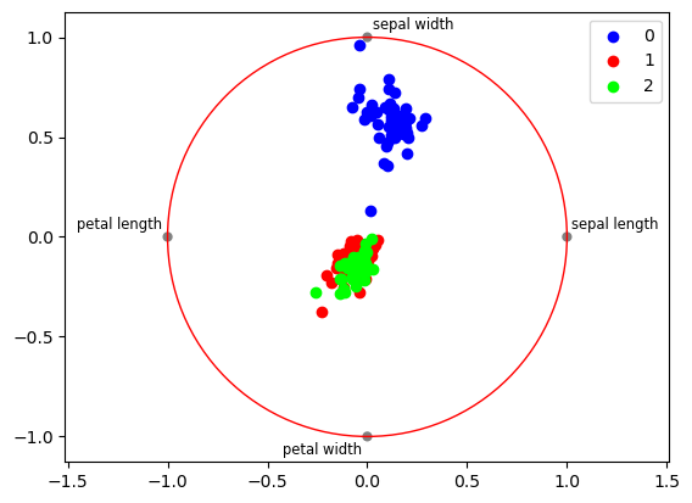
径向可视化
用于观察每种类别花的四个特征之间的相对关系(线性大小关系)。
如下图,其中0、1、2分别对应Setosa,Versicolour,Virginica类别,可以直观看出:Setosa花的花萼宽度(Speal Width)和花萼长度(Speal Length)这两个特征相比其他两个特征花瓣宽度(Petal Width)和花瓣长度(Petal Length)具有区分性,而Versicolour,Virginica花的四个特征分布很相似,不好区分。
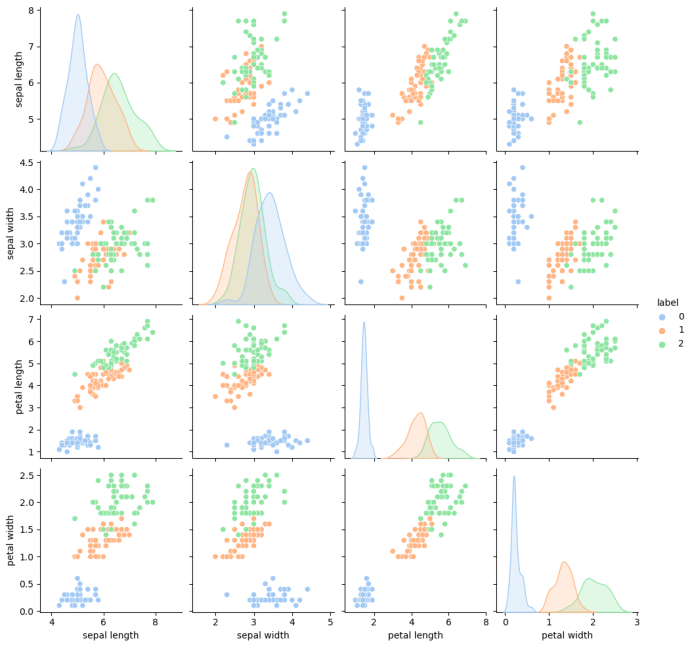
各个特征之间的关系图
从下图可以看出,Setosa花的花瓣宽度(Petal Width)和花瓣长度(Petal Length)的分布相比其他两类具有很好的区分性。
🧡🧡支持向量机SVM求解🧡🧡
直觉理解:
对于二维特征,如何区分图中不同的点
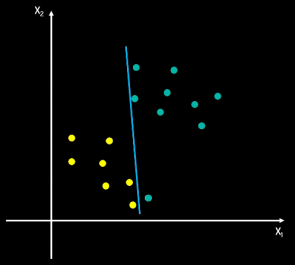
第一种思路:如下左图画一条线,但是是一个不太好的分割线
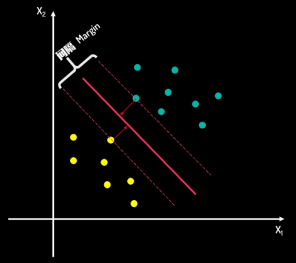
而换一种思路,如下右图,先找两个分类的决策边界(两边的虚线)之间的间隔区域,再取间隔区域的中间为分割线,这样能保证分割效果最佳。因此寻找最佳决策边界线(中间线)的问题可以转化为求解两类数据的最大间隔问题。
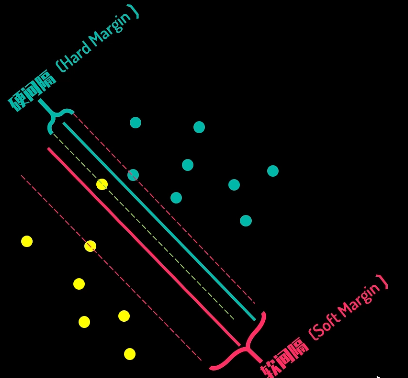
因此将决策边界上下移动c,得到间隔的两个边界线,如下左图,此时这两个边界线称为支持向量,它们决定了间隔距离。如下右图,经过数学变换,可以得到最终要求的超平面表达式,即求解参数w、b即可
除此之外,只考虑分类点的决策边界之间的距离的间隔,称为硬间隔,同时考虑距离和异常点损失(下图红线上方的黄点)的间隔,称为软间隔。
数学推导
某点到超平面的距离r:(几何间隔,可以代表分类正确的确信度)
目标超平面之间的间隔距离γ:
约束条件:点到超平面距离r >= 超平面间隔距离γ的一半:
则最终求解的函数表达式为:
但是以上函数表达式为非凸函数,因此要:
- 先转为凸函数
- 用拉格朗日乘子法和KKT条件求解对偶问题
1.转为凸函数:
2.用拉格朗日乘子法和KKT条件求解对偶问题
这个过程就涉及到高阶的数学知识了,我这里也不是很懂,只大概了解:
为什么要用拉格朗日乘子法:将不等式约束转换为等式约束。
整合成如下拉格朗日表达式:
依据对偶性,求解问题为:
先求解:
根据KKT条件:对w、b求偏导可得:
代入L(w,b,a):
再求解:
3.利用SMO求解α、从而求解w、b
现在优化问题变成了如上的形式,但是它的规模正比于训练样本数m,当m很大时,会有很大开销,因此针对这个问题的特性,有更高效的优化算法,即序列最小优化(SMO)算法。
其大概思想是:先固定α以外的参数,然后对α求极值,在上述约束条件下,α可以由其他变量导出,这样,在参数初始化后,不断迭代,可以最终达到收敛。
通过SMO求得的w、b为:
则超平面的公式为:
最后根据超平面的符号,表达成分类决策函数即可:
代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScalerclass SMO:def __init__(self, X, y, C, kernel, tol, max_passes=10):self.X = X # 样本特征 m*n m个样本 n个特征self.y = y # 样本标签 m*1self.C = C # 惩罚因子, 用于控制松弛变量的影响self.kernel = kernel # 核函数self.tol = tol # 容忍度self.max_passes = max_passes # 最大迭代次数self.m, self.n = X.shapeself.alpha = np.zeros(self.m)self.b = 0self.w = np.zeros(self.n)# 计算核函数def K(self, i, j):if self.kernel == 'linear':return np.dot(self.X[i].T, self.X[j])elif self.kernel == 'rbf':gamma = 0.5return np.exp(-gamma * np.linalg.norm(self.X[i] - self.X[j]) ** 2)else:raise ValueError('Invalid kernel specified')def predict(self, X_test):pred = np.zeros_like(X_test[:, 0])pred = np.dot(X_test, self.w) + self.breturn np.sign(pred)def train(self):"""训练模型:return:"""passes = 0while passes < self.max_passes:num_changed_alphas = 0for i in range(self.m):# 计算E_i, E_i = f(x_i) - y_i, f(x_i) = w^T * x_i + b# 计算误差E_iE_i = 0for ii in range(self.m):E_i += self.alpha[ii] * self.y[ii] * self.K(ii, i)E_i += self.b - self.y[i]# 检验样本x_i是否满足KKT条件if (self.y[i] * E_i < -self.tol and self.alpha[i] < self.C) or (self.y[i] * E_i > self.tol and self.alpha[i] > 0):# 随机选择样本x_jj = np.random.choice(list(range(i)) + list(range(i + 1, self.m)), size=1)[0]# 计算E_j, E_j = f(x_j) - y_j, f(x_j) = w^T * x_j + b# E_j用于检验样本x_j是否满足KKT条件E_j = 0for jj in range(self.m):E_j += self.alpha[jj] * self.y[jj] * self.K(jj, j)E_j += self.b - self.y[j]alpha_i_old = self.alpha[i].copy()alpha_j_old = self.alpha[j].copy()# L和H用于将alpha[j]调整到[0, C]之间if self.y[i] != self.y[j]:L = max(0, self.alpha[j] - self.alpha[i])H = min(self.C, self.C + self.alpha[j] - self.alpha[i])else:L = max(0, self.alpha[i] + self.alpha[j] - self.C)H = min(self.C, self.alpha[i] + self.alpha[j])# 如果L == H,则不需要更新alpha[j]if L == H:continue# eta: alpha[j]的最优修改量eta = 2 * self.K(i, j) - self.K(i, i) - self.K(j, j)# 如果eta >= 0, 则不需要更新alpha[j]if eta >= 0:continue# 更新alpha[j]self.alpha[j] -= (self.y[j] * (E_i - E_j)) / eta# 根据取值范围修剪alpha[j]self.alpha[j] = np.clip(self.alpha[j], L, H)# 检查alpha[j]是否只有轻微改变,如果是则退出for循环if abs(self.alpha[j] - alpha_j_old) < 1e-5:continue# 更新alpha[i]self.alpha[i] += self.y[i] * self.y[j] * (alpha_j_old - self.alpha[j])# 更新b1和b2b1 = self.b - E_i - self.y[i] * (self.alpha[i] - alpha_i_old) * self.K(i, i) \- self.y[j] * (self.alpha[j] - alpha_j_old) * self.K(i, j)b2 = self.b - E_j - self.y[i] * (self.alpha[i] - alpha_i_old) * self.K(i, j) \- self.y[j] * (self.alpha[j] - alpha_j_old) * self.K(j, j)# 根据b1和b2更新bif 0 < self.alpha[i] and self.alpha[i] < self.C:self.b = b1elif 0 < self.alpha[j] and self.alpha[j] < self.C:self.b = b2else:self.b = (b1 + b2) / 2num_changed_alphas += 1if num_changed_alphas == 0:passes += 1else:passes = 0# 提取支持向量和对应的参数idx = self.alpha > 0 # 支持向量的索引# SVs = X[idx]selected_idx = np.where(idx)[0]SVs = self.X[selected_idx]SV_labels = self.y[selected_idx]SV_alphas = self.alpha[selected_idx]# 计算权重向量和截距self.w = np.sum(SV_alphas[:, None] * SV_labels[:, None] * SVs, axis=0)self.b = np.mean(SV_labels - np.dot(SVs, self.w))print("w", self.w)print("b", self.b)def score(self, X, y):predict = self.predict(X)print("predict", predict)print("target", y)return np.mean(predict == y)# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
y[y != 0] = -1
y[y == 0] = 1 # 分成两类# 为了方便可视化,只取前两个特征
X2 = X[:,:2]
# # 分别画出类别 0 和 1 的点
plt.scatter(X2[y == 1, 0], X2[y == 1, 1], color='red',label="class 1")
plt.scatter(X2[y == -1, 0], X2[y == -1, 1], color='blue',label="class -1")
plt.xlabel("Speal Width")
plt.ylabel("Speal Length")
plt.legend()
plt.show()# 数据预处理,将特征进行标准化,并将数据划分为训练集和测试集
scaler = StandardScaler()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3706)
X_train_std = scaler.fit_transform(X_train)# 创建SVM对象并训练模型
svm = SMO(X_train_std, y_train, C=0.6, kernel='rbf', tol=0.001)
svm.train()# 预测测试集的结果并计算准确率
X_test_std = scaler.transform(X_test)
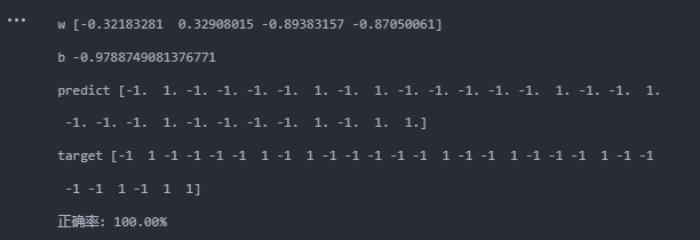
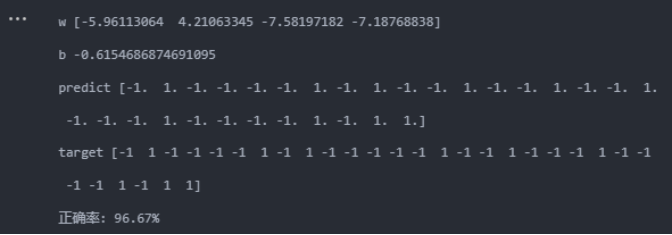
accuracy = svm.score(X_test_std, y_test)
print('正确率: {:.2%}'.format(accuracy))from sklearn.metrics import confusion_matrix, roc_curve, auc
y_pred=svm.predict(X_test_std)# 绘制混淆矩阵
def cal_ConfusialMatrix(y_true_labels, y_pred_labels):cm = np.zeros((2, 2))y_true_labels = [0 if x == -1 else x for x in y_true_labels]y_pred_labels = [0 if x == -1 else x for x in y_pred_labels]for i in range(len(y_true_labels)):cm[ y_true_labels[i], y_pred_labels[i] ] += 1plt.figure(figsize=(8, 6))sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=['Predicted Negative', 'Predicted Positive'], yticklabels=['Actual Negative', 'Actual Positive'])plt.xlabel('Predicted label')plt.ylabel('True label')plt.title('Confusion Matrix')plt.show()y_pred=[int(x) for x in y_pred]
y_test=[int(x) for x in y_test]
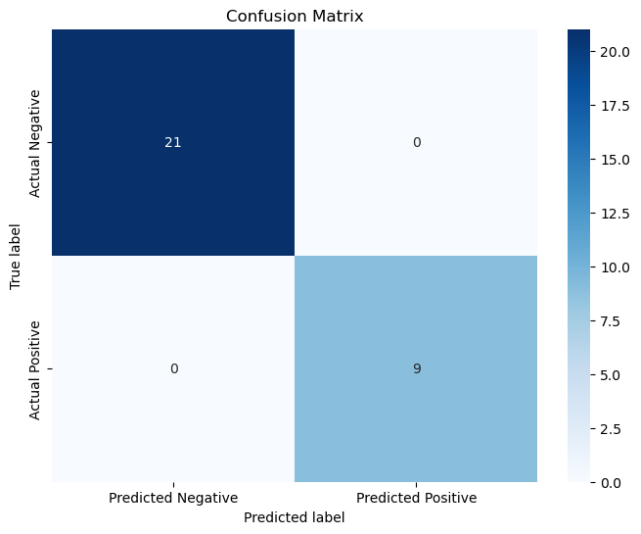
cal_ConfusialMatrix(y_test, y_pred)运行结果
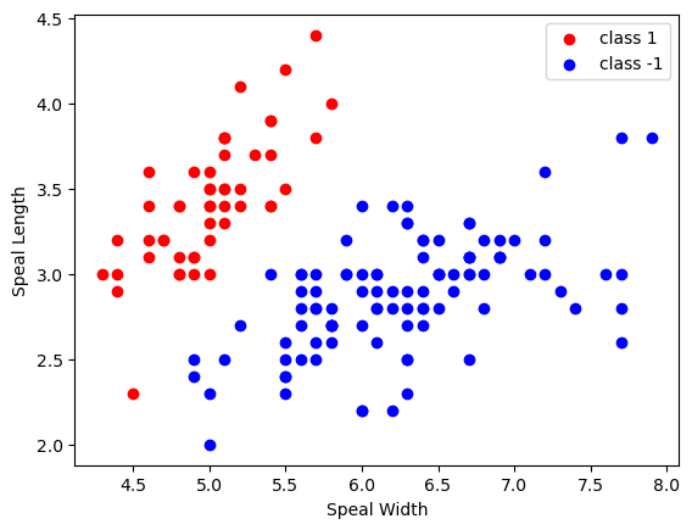
由于鸢尾花为三分类,为了简化实验,这里先把setosa定义为1类(+1),versicolor、virginica组合定义为1类(-1)。
做出其对于sepal width和sepal length的分布图,可以看到,训练样本应该是线性可分的。
按照训练集:测试集=8:2的比例进行训练,之后进行测试集分类结果如下:
线性核:
高斯核:
🧡🧡总结🧡🧡
实验结果:
当使用的核函数为线性核时,准确率能达到100%,而使用高斯核时,准确率降低到96.67%(其实从混淆矩阵可以看到,只分类错误1个),且运行时间相对长很多。
分析原因:
线性核适用于数据集具有线性可分性的情况,即类别之间可以通过一条直线进行划分。在这种情况下,线性核可以提供较好的分类性能,并且计算效率较高。
高斯核可以更好地处理非线性问题。高斯核可以将输入空间映射到一个更高维度的特征空间,从而使得数据在新的特征空间中更容易被线性分割。但是,高斯核也有其缺点:在使用高斯核时,需要调整的超参数较多,如 gamma 参数和正则化参数 C,不正确的参数选择可能导致过拟合或欠拟合的问题。此外,高斯核计算复杂度较高,需要计算每个样本与其他样本之间的相似度,因此在数据集上的训练和预测时间可能较长。
因此综合分析,本实验中鸢尾花的特征为线性,因此使用线性核效果更佳。同时高斯核对参数比较敏感,实验中对于高斯核的参数选择可能也不够恰当。
相关文章:
机器学习实验3——支持向量机分类鸢尾花
文章目录 🧡🧡实验内容🧡🧡🧡🧡数据预处理🧡🧡代码认识数据相关性分析径向可视化各个特征之间的关系图 🧡🧡支持向量机SVM求解🧡🧡直觉…...
:移除孤立的记录)
R语言【taxlist】——clean():移除孤立的记录
Package taxlist version 0.2.4 Description 对于 taxlist 类对象的操作可能会产生独立的条目。clean() 方法就是用来删除这样的条目,并恢复 taxlist 对象的一致性。 Usage clean(object, ...)## S4 method for signature taxlist clean(object, times 2, ...) A…...

CentOS 7.9 OS Kernel Update 3.10 to 4.19
date: 2024-01-18, 2024-01-26 原 OS Kernel 3.10 升级至 4.19 1.检查默认内核 检查 vmlinuz 版本 [rootlocalhost ~]# grubby --default-kernel /boot/vmlinuz-3.10.0-1160.105.1.el7.x86_64 [rootlocalhost ~]#检查 Linux 内核版本 [rootlocalhost ~]# uname -a Linux loc…...

k8s---安全机制
k8s的安全机制,分布式集群管理工具,就是容器编排。安全机制的核心:APIserver。为整个集群内部通信的中介,也是外控控制的入口。所有的机制都是围绕apiserver来进行设计: 请求api资源: 1、认证 2、鉴权 …...
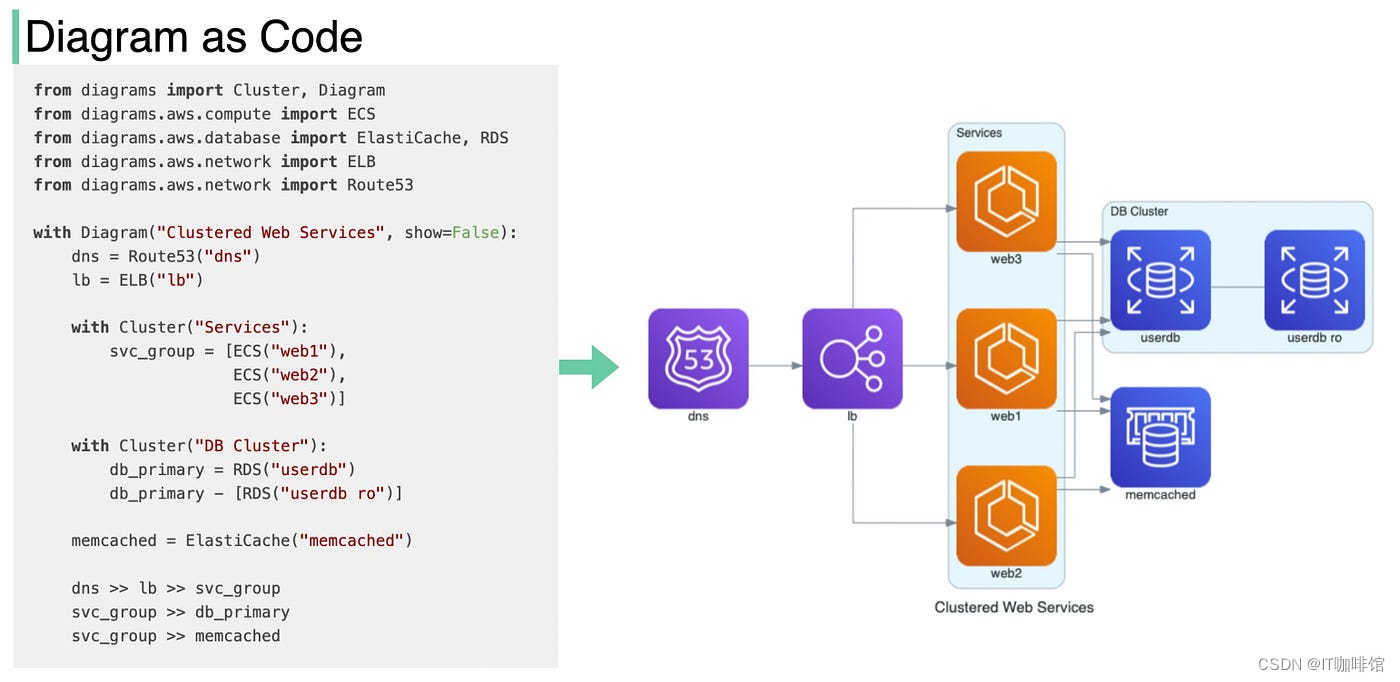
GitHub 一周热点汇总第7期(2024/01/21-01/27)
GitHub一周热点汇总第7期 (2024/01/21-01/27) ,梳理每周热门的GitHub项目,离春节越来越近了,不知道大家都买好回家的票没有,希望大家都能顺利买到票,一起来看看这周的项目吧。 #1 rustdesk 项目名称:rust…...

kotlin data clas 数据类
data class 介绍 kotlin 中 data class 是一种持有数据的特殊类 编译器自动从主构造函数中声明的所有属性导出以下成员: .equals()/.hashCode() 对 .toString() 格式是 "User(nameJohn, age42)" .componentN() 函数 按声明顺序对应于所有属性。…...

Java基础知识-异常
资料来自黑马程序员 异常 异常,就是不正常的意思。在生活中:医生说,你的身体某个部位有异常,该部位和正常相比有点不同,该部位的功能将受影响.在程序中的意思就是: 异常 :指的是程序在执行过程中,出现的非正常的情况,…...
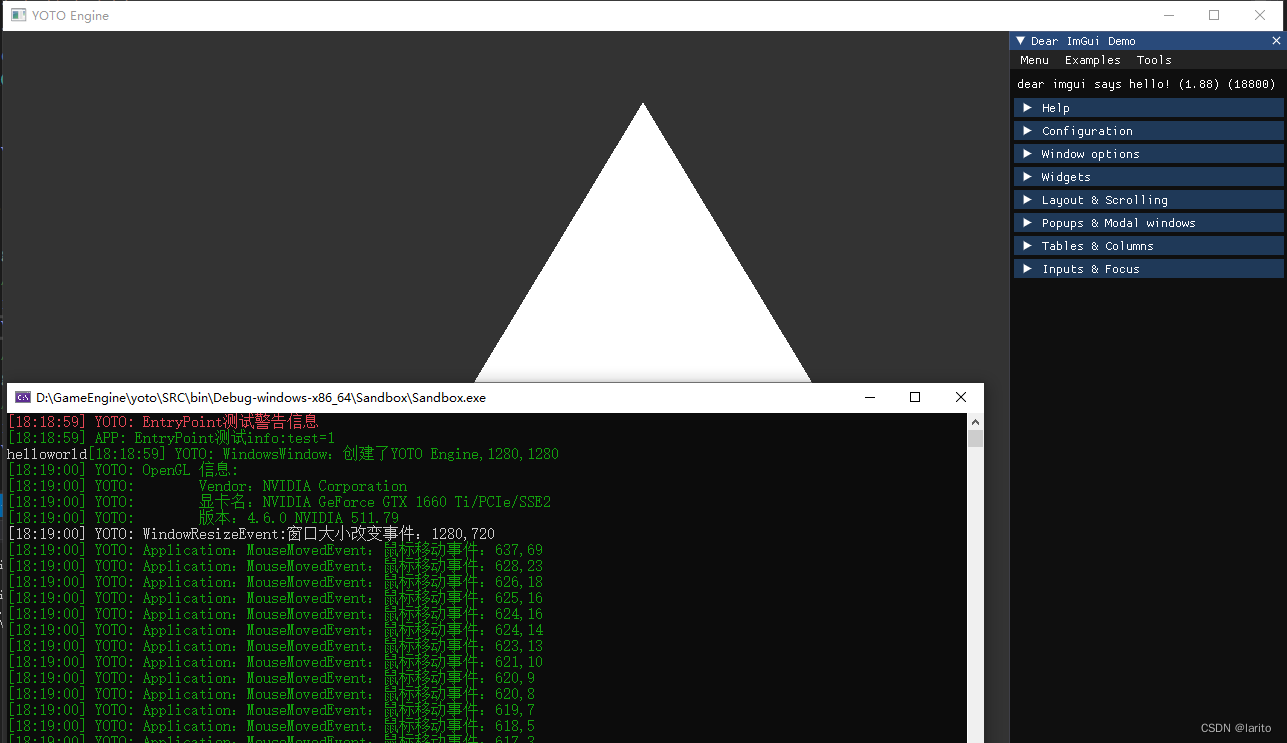
跟着cherno手搓游戏引擎【12】渲染context和首个三角形
渲染上下文: 目的:修改WindowsWindow的结构,把glad抽离出来 WindowsWindow.h:新建m_Context #pragma once #include "YOTO/Window.h" #include <YOTO/Renderer/GraphicsContext.h> #include<GLFW/glfw3.h> #include…...

MybatisPlus二级映射和关联对象ResultMap
文章目录 一、业务背景1. 数据库表结构2. 需求 二、使用映射直接得到指定结构三、其他文件1. Mapper2. Service3. Controller 四、概念理解一级映射二级映射聚合 五、标签使用1. \<collection\> 标签2. \<association\> 标签 在我们的教程中,我们设计了…...

低代码开发业务在AIGC时代的应用
随着人工智能和图形计算能力的快速发展,低代码开发平台在AIGC(人工智能,物联网,大数据和云计算)时代中扮演着至关重要的角色。本文将介绍低代码开发业务的概念和优势,探讨其在AIGC时代的应用及其对传统软件…...

惠普1536dnf MFP报52扫描仪错误维修
如果您使用的惠普HP LaserJet 1536dnf MFP打印机可能会遇到“52扫描仪错误”的提示。这个错误可能会阻止你使用打印机的扫描功能。在这里,我将提供一些有用的解决方法来帮助大家去解决这个问题。-----吴中函 故障描述: 一台某单位正在使用的惠普HP LaserJet 1536dnf MFP黑白…...

【MIdjourney】五个特殊物体关键词
1.碳酸(Carbonate) 这一词语的本意是指包含碳(C)、氧(O)和氢(H)元素的化合物。而在MIdjourney中添加该词汇会使得生成的图片具有水滴效果且富有动态感。 2.灯丝(Filament) Filament效果可能包括更逼真的…...

2024/1/27 备战蓝桥杯 1
目录 求和 0求和 - 蓝桥云课 (lanqiao.cn) 成绩分析 0成绩分析 - 蓝桥云课 (lanqiao.cn) 合法日期 0合法日期 - 蓝桥云课 (lanqiao.cn) 时间加法 0时间加法 - 蓝桥云课 (lanqiao.cn) 扫雷 0扫雷 - 蓝桥云课 (lanqiao.cn) 大写 0大写 - 蓝桥云课 (lanqiao.cn) 标题…...

初学数据结构:Java对象的比较
目录 1. PriorityQueue中插入对象2. 元素的比较2.1 基本类型的比较2.2 对象比较的问题 3. 对象的比较3.1 基于Comparable接口类的比较3.2 基于比较器比较3.3 三种方式对比 4. 集合框架中PriorityQueue的比较方式5. 使用PriorityQueue创建大小堆,解决TOPK问题 【本节…...

mac 10.15.7 Unity 2021.3.14 XCode 12.4 -> Unity IOS 自动安装 Cocoapods 失败解决方法
自己这两天在用Unity开发IOS时,遇到了安装Cocoapods失败的问题,记录一下问题及解决方法,便于自己后续查看,以及有相同遭遇的人查看 发生场景:打开 unity,触发自动安装 Cocoapods -> 安装失败(…...

Elasticsearch 中使用MustNot等同于不登录遇到的坑
1、在写关键词推荐时,需要把当前文章过滤掉,不能再推荐自己的文章,所以再es中需要用到 MustNot属性查询 /// <summary> /// 服务中心es检索 /// </summary> /// <param name="input"></param> /// <returns></…...

java抽象工厂实战与总结
文章目录 一、工厂模式(三种)1.简单工厂模式1.1 概念:1.2 使用场景:1.3 模型图解:1.4 伪代码: 2.工厂方法模式2.1 概念:2.2 使用场景:2.3 模型图解:2.4 伪代码 3.抽象工厂…...
 | 选择框)
Compose | UI组件(六) | 选择框
文章目录 前言Checkbox 复选框的含义Checkbox 复选框的使用Switch 单选框的含义Switch 单选框的使用Slider 滑竿组件的含义Slider 滑竿组件的使用 总结 前言 随着移动端的技术不断更新迭代,Compose也运用的越来越广泛,很多人都开始学习Compose 本文主要…...

C++拷贝构造函数、赋值学习整理:
拷贝构造函数: 概念: 构造函数的第一个参数,是类本身的const引用(一般情况下没有其他参数,少数情况:其他参数必须有默认值!)称此类构造函数为拷贝构造函数 特征: 1&am…...
[亲测源码]ps软件网页版在线使用 PS网站程序源码 photoshop网页版源码 网页版的ps软件源码
在线PS作图修图网页版PHP网站源码,PHP在线照片图片处理PS网站程序源码photoshop网页版。 有很多朋友们都是在用PS作图的,众所周知在使用和学习PS时是需要下载软件的,Photoshop软件对电脑配置也是有一定要求的,今天就为大家带来一…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...