2024.1.26力扣每日一题——计算 K 置位下标对应元素的和
2024.1.26
- 题目来源
- 我的题解
- 方法一 位运算+统计二进制数中1的个数
- 方法二 官方的一种优化计算二进制中1的个数的方法
题目来源
力扣每日一题;题序:2859
我的题解
方法一 位运算+统计二进制数中1的个数
对于每一个位置i都去计算i对应的二进制数中1的个数
时间复杂度:O( n log n u m n\log num nlognum)。 log n u m \log num lognum表示求二进制数中1的个数所需的时间
空间复杂度:O(1)
public int sumIndicesWithKSetBits(List<Integer> nums, int k) {int n=nums.size();int res=0;for(int i=0;i<n;i++){if(countOnes(i)==k)res+=nums.get(i);}return res;
}
public int countOnes(int n){int res=0;while(n>0){res+=(n&1)==1?1:0;n=n>>1;}return res;
}
方法二 官方的一种优化计算二进制中1的个数的方法
官方题解
这个没看懂,大家自己去看官方题解吧
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

2024.1.26力扣每日一题——计算 K 置位下标对应元素的和
2024.1.26 题目来源我的题解方法一 位运算统计二进制数中1的个数方法二 官方的一种优化计算二进制中1的个数的方法 题目来源 力扣每日一题;题序:2859 我的题解 方法一 位运算统计二进制数中1的个数 对于每一个位置i都去计算i对应的二进制数中1的个数 …...
:获取或设置分类等级列表)
R语言【taxlist】——levels():获取或设置分类等级列表
Package taxlist version 0.2.4 Description 分类层次结构可以设置为 taxlist 对象中的级别,按从低到高的顺序排列。 在 taxlist 对象中为特定分类概念添加分类级别。此外,概念限制的变化可能涉及其分类层次结构的变化。 Usage levels(x)## S3 method…...

单元测试——题目十三
目录 题目要求: 定义类 测试类 题目要求: 根据输入的三条边值判断能组成何种三角形。三条边为变量a、b、c,范围为1≤边值≤10,不在范围内,提示“输入边值不在范围内”。不满足任意两边之和必须大于第三边,提示“输入边值不能组成三角形”。输入边值能组成三角形,只有…...
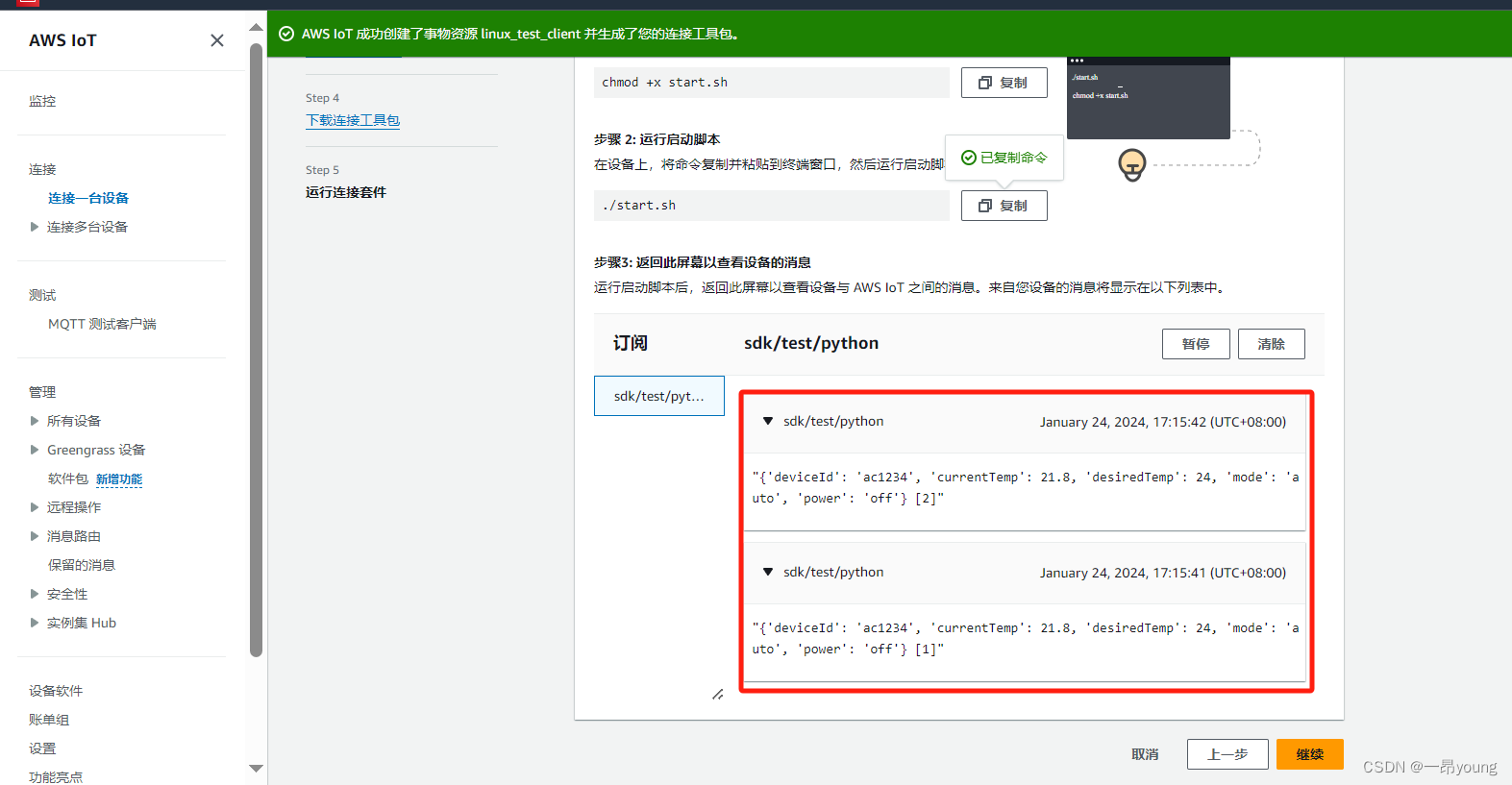
使用Linux SDK客户端向AWS Iot发送数据
参考链接: https://ap-southeast-1.console.aws.amazon.com/iot/home?regionap-southeast-1#/test 此篇文章用于测试,使用Linux SDK客户端向AWS Iot发送数据,准备环境如下: 1、客户端环境准备 1.1 客户端操作系统 虚拟机一台…...

1.27学习总结
今天做了些队列的题: 1.逛画展(单调队列) 2.打印队列 Printer Queue(优先队列) 3.[NOIP2010 提高组] 机器翻译(模拟队列) 4.求m区间内的最小值(单调队列板子题) 5.日志统计(滑动窗口,双指针) 总结一下&…...

【算法专题】二分查找(进阶)
📑前言 本文主要是二分查找(进阶)的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 🌄每日…...

开源项目对于新用户和初学者适合哪些工作
目录 一、阅读和理解文档 二、报告问题 三、测试和验证修复 四、编写和更新文档 五、简单的代码更改和修复 六、参与社区讨论 开源项目对于新用户和初学者来说,提供了宝贵的学习和实践机会。以下是一些适合新用户和初学者参与的工作: 一、阅读和理…...

linux中配置文件目录为什么用etc来命名
在早期的 Unix 系统中,/etc 目录的名称确实来源于单词 “etcetera” 的缩写,最初意味着 “其他”,用来存放杂项或者不属于其他特定目录的文件。然而,随着时间的推移,/etc 目录的用途逐渐演变并专门化。 在现代的 Linux…...
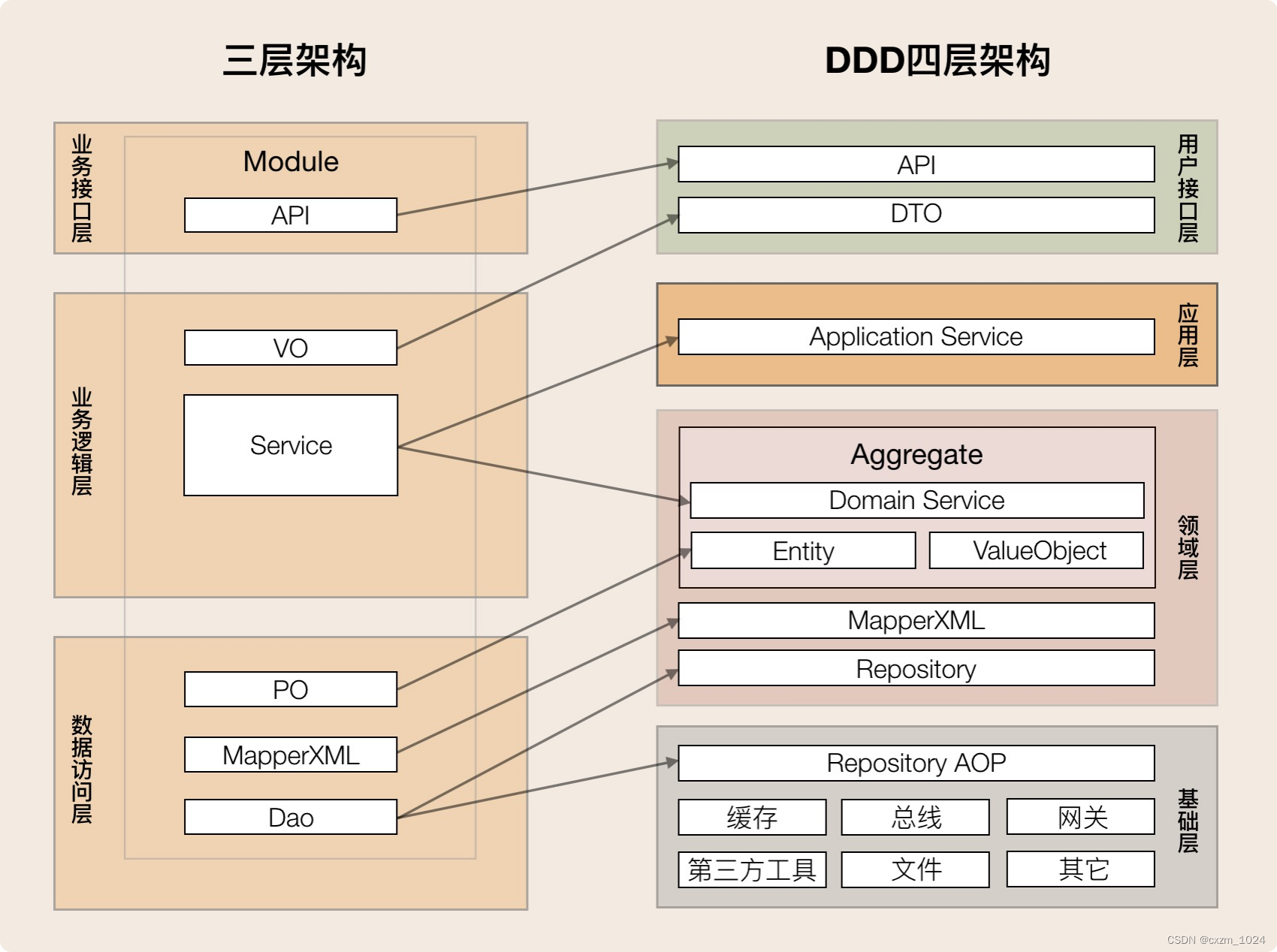
06.领域驱动设计:使用DDD分层架构,可以有效降低层与层之间的依赖
目录 1、概述 2、什么是DDD分层架构 1.用户接口层 2.应用层 3.领域层 4.基础层 3、DDD分层架构最重要的原则是什么 4、DDD分层架构如何推动架构演进 1.微服务架构的演进 2.微服务内服务的演进 5、三层架构如何演进到DDD分层架构 我们该怎样转向DDD分层架构 6、总结…...

HCIA-Datacom实验指导手册:3.2 实验二:生成树基础实验
HCIA-Datacom实验指导手册:3.2 实验二:生成树基础实验 一、实验介绍:二、实验拓扑:三、实验目的:四、配置步骤:步骤 1 掌握启用和禁用 STP/RSTP 的方法步骤 2 掌握修改交换机 STP 模式的方法步骤 3 掌握修改桥优先级,控制根桥选举的方法步骤 4 掌握修改端口优先级,控制…...

WPF的ViewBox控件
在WPF中,ViewBox是一个用于缩放和调整其子元素大小的容器控件。它可以根据可用空间自动调整子元素的大小,以使其适应ViewBox的边界。这使得在不同尺寸的窗口或布局中保持元素的比例和缩放变得更加容易。 ViewBox具有以下重要属性: Stretch&…...
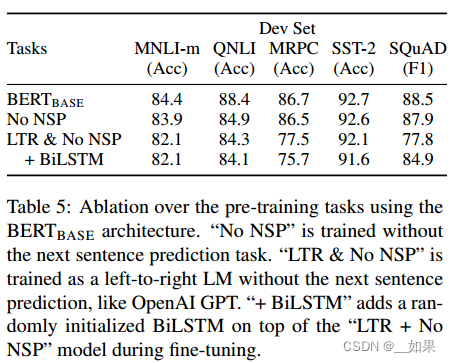
论文精读--BERT
不像视觉领域,在Bert出现之前的nlp领域还没有一个深的网络,使得能在大数据集上训练一个深的神经网络,并应用到很多nlp的任务上 Abstract We introduce a new language representation model called BERT, which stands for Bidirectional En…...

LeetCode第468题 - 验证IP地址
题目 编写一个函数来验证输入的字符串是否是有效的 IPv4 或 IPv6 地址。 IPv4 地址由十进制数和点来表示,每个地址包含4个十进制数,其范围为 0 - 255, 用(“.”)分割。比如,172.16.254.1; 同时,IPv4 地址内…...

淘宝API接口调用:案例分析与最佳实践
在电子商务迅猛发展的今天,淘宝作为中国最大的在线购物平台之一,为商家们提供了强大的数据分析和市场洞察工具——淘宝API。有效的API调用不仅可以提升商家的运营效率,还可以帮助商家更好地理解消费者需求、优化商品布局、提高用户满意度等。…...

中仕教育:事业单位考试考什么?
事业单位考试分为两个阶段,分别是笔试和面试,考试科目包括公共科目和专业科目两部分。 公共科目内容是公共基础知识、职业能力测试或申论。一种形式为:公共基础知识职业能力测试或职业能力测试申论。另一种形式为:公共基础申论。…...

python-自动化篇-运维-监控-简单实例-道出如何使⽤Python进⾏系统监控?
如何使⽤Python进⾏系统监控? 使⽤Python进⾏系统监控涉及以下⼀般步骤: 选择监控指标: ⾸先,确定希望监控的系统指标,这可以包括 CPU 利⽤率、内存使⽤情况、磁盘空间、⽹络流量、服务可⽤性等。选择监控⼯具&#x…...

网络安全科普:SSL证书保护我们的网上冲浪安全
当我们在线上愉快冲浪时,各类网站数不胜数,但是如何判定该站点是安全还是有风险呢? 当当当,SSL数字证书登场!! SSL证书也称为数字证书,是一种用于保护网站和用户之间通信安全的加密协议。由权…...

AOP复习
AOP AOP静态代理动态代理ProxyCGLIB AOP 面向切面编程 优点: 提高代码的可重用性业务代码编码更简洁业务代码维护更高效业务功能扩展更便捷 Joinpoint(连接点)就是方法Pointcut(切入点)就是挖掉共性功能的方法Advice(通知)就是共性功能,最终以一个方法的形式呈现Asp…...

解决 Required Integer parameter ‘uid‘ is not present
1.原因分析 后端没接收到uid可能是前端没传递uid也可能是前端传递了uid,但是传递方式与后端接收方式不匹配,导致没接收到更大的可能是因为后端请求方式错了。比如: 2.解决方案 先确定前端传参方式与后端请求方式是匹配的后端get请求的话…...

Qt/QML编程之路:ListView实现横排图片列表的示例(40)
ListView列表,在QML中使用非常多,排列一个行,一个列或者一个表格,都会用到ListView。 ListView显示从内置QML类型(如ListModel和XmlListModel)创建的模型中的数据,或在C++中定义的从QAbstractItemModel或QAbstract ListModel继承的自定义模型类中的数据。 ListView有一…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
