《动手学深度学习(PyTorch版)》笔记3.1
Chapter3 Linear Neural Networks
3.1 Linear Regression
3.1.1 Basic Concepts
我们通常使用 n n n来表示数据集中的样本数。对索引为 i i i的样本,其输入表示为 x ( i ) = [ x 1 ( i ) , x 2 ( i ) , . . . , x n ( i ) ] ⊤ \mathbf{x}^{(i)} = [x_1^{(i)}, x_2^{(i)},...,x_n^{(i)}]^\top x(i)=[x1(i),x2(i),...,xn(i)]⊤,其对应的标签是 y ( i ) y^{(i)} y(i)。
3.1.1.1 Linear Model
在机器学习领域,我们通常使用的是高维数据集,建模时采用线性代数表示法会比较方便。当我们的输入包含 d d d个特征时,我们将预测结果 y ^ \hat{y} y^(通常使用“尖角”符号表示 y y y的估计值)表示为:
y ^ = w 1 x 1 + . . . + w d x d + b . \hat{y} = w_1 x_1 + ... + w_d x_d + b. y^=w1x1+...+wdxd+b.
将所有特征放到向量 x ∈ R d \mathbf{x} \in \mathbb{R}^d x∈Rd中,并将所有权重放到向量 w ∈ R d \mathbf{w} \in \mathbb{R}^d w∈Rd中,我们可以用点积形式来简洁地表达模型:
y ^ = w ⊤ x + b (1) \hat{y} = \mathbf{w}^\top \mathbf{x} + b \tag{1} y^=w⊤x+b(1)
在式(1)中,向量 x \mathbf{x} x对应于单个数据样本的特征。用符号表示的矩阵 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d可以很方便地引用我们整个数据集的 n n n个样本。其中, X \mathbf{X} X的每一行是一个样本,每一列是一种特征。对于特征集合 X \mathbf{X} X,预测值 y ^ ∈ R n \hat{\mathbf{y}} \in \mathbb{R}^n y^∈Rn可以通过矩阵-向量乘法表示为:
y ^ = X w + b {\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b y^=Xw+b
给定训练数据特征 X \mathbf{X} X和对应的已知标签 y \mathbf{y} y,线性回归的目标是找到一组权重向量 w \mathbf{w} w和偏置 b b b:当给定从 X \mathbf{X} X的同分布中取样的新样本特征时,这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。
虽然我们相信给定 x \mathbf{x} x预测 y y y的最佳模型会是线性的,但我们很难找到一个有 n n n个样本的真实数据集,其中对于所有的 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n, y ( i ) y^{(i)} y(i)完全等于 w ⊤ x ( i ) + b \mathbf{w}^\top \mathbf{x}^{(i)}+b w⊤x(i)+b。无论我们使用什么手段来观察特征 X \mathbf{X} X和标签 y \mathbf{y} y,都可能会出现少量的观测误差。因此,即使确信特征与标签的潜在关系是线性的,我们也会加入一个噪声项来考虑观测误差带来的影响。
在开始寻找最好的模型参数(model parameters w \mathbf{w} w和 b b b之前,
我们还需要两个东西:
- 一种模型质量的度量方式;
- 一种能够更新模型以提高模型预测质量的方法。
3.1.1.2 Loss Function
在我们开始考虑如何用模型拟合(fit)数据之前,我们需要确定一个拟合程度的度量。
损失函数(loss function)能够量化目标的实际值与预测值之间的差距。通常我们会选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。回归问题中最常用的损失函数是平方误差函数。当样本 i i i的预测值为 y ^ ( i ) \hat{y}^{(i)} y^(i),其相应的真实标签为 y ( i ) y^{(i)} y(i)时,
平方误差可以定义为以下公式:
l ( i ) ( w , b ) = 1 2 ( y ^ ( i ) − y ( i ) ) 2 . l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2. l(i)(w,b)=21(y^(i)−y(i))2.
常数 1 2 \frac{1}{2} 21不会带来本质的差别,但这样在形式上稍微简单一些(因为当我们对损失函数求导后常数系数为1)。由于训练数据集并不受我们控制,所以经验误差只是关于模型参数的函数。由于平方误差函数中的二次方项,估计值 y ^ ( i ) \hat{y}^{(i)} y^(i)和观测值 y ( i ) y^{(i)} y(i)之间较大的差异将导致更大的损失。为了度量模型在整个数据集上的质量,我们需计算在训练集 n n n个样本上的损失均值(也等价于求和)。
L ( w , b ) = 1 n ∑ i = 1 n l ( i ) ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2 . L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2. L(w,b)=n1i=1∑nl(i)(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2.
在训练模型时,我们希望寻找一组参数( w ∗ , b ∗ \mathbf{w}^*, b^* w∗,b∗),这组参数能最小化在所有训练样本上的总损失。如下式:
w ∗ , b ∗ = argmin w , b L ( w , b ) . \mathbf{w}^*, b^* = \operatorname*{argmin}_{\mathbf{w}, b}\ L(\mathbf{w}, b). w∗,b∗=w,bargmin L(w,b).
3.1.1.3 Analytical Solution
线性回归有解析解(analytical solution)。首先,我们将偏置 b b b合并到参数 w \mathbf{w} w中,合并方法是在包含所有参数的矩阵中附加一列。我们的预测问题是最小化 ∥ y − X w ∥ 2 \|\mathbf{y} - \mathbf{X}\mathbf{w}\|^2 ∥y−Xw∥2。这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。将损失关于 w \mathbf{w} w的导数设为0,即
X ⊤ X w = X ⊤ y \mathbf X^\top \mathbf{X}\mathbf{w}=\mathbf X^\top \mathbf{y} X⊤Xw=X⊤y
得到解析解:
w ∗ = ( X ⊤ X ) − 1 X ⊤ y \mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y} w∗=(X⊤X)−1X⊤y
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。
3.1.1.4 Stochastic Gradient Descent
我们用到一种名为梯度下降(gradient descent)的方法,几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值)关于模型参数的导数(在这里也可以称为梯度)。但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本,这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)。
在每次迭代中,我们首先随机抽样一个小批量 B \mathcal{B} B,它是由固定数量的训练样本组成的。然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。最后,我们将梯度乘以一个预先确定的正数 η \eta η,并从当前参数的值中减掉。
我们用下面的数学公式来表示这一更新过程,其中 w \mathbf{w} w和 x \mathbf{x} x都是向量, ∣ B ∣ |\mathcal{B}| ∣B∣表示每个小批量中的样本数,称为批量大小(batch size)。
η \eta η表示学习率(learning rate)。
( w , b ) ← ( w , b ) − η ∣ B ∣ ∑ i ∈ B ∂ ( w , b ) l ( i ) ( w , b ) . (\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b). (w,b)←(w,b)−∣B∣ηi∈B∑∂(w,b)l(i)(w,b).
总而言之,算法的步骤如下:
(1)初始化模型参数的值,如随机初始化;
(2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
对于平方损失和仿射变换,可以写成如下形式:
w ← w − η ∣ B ∣ ∑ i ∈ B ∂ w l ( i ) ( w , b ) = w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) (关于 w 的偏导) b ← b − η ∣ B ∣ ∑ i ∈ B ∂ b l ( i ) ( w , b ) = b − η ∣ B ∣ ∑ i ∈ B ( w ⊤ x ( i ) + b − y ( i ) ) (关于 b 的偏导) \begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right) \text{ (关于$\mathbf{w}$的偏导)}\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right) \text{ (关于$b$的偏导)} \end{aligned} wb←w−∣B∣ηi∈B∑∂wl(i)(w,b)=w−∣B∣ηi∈B∑x(i)(w⊤x(i)+b−y(i)) (关于w的偏导)←b−∣B∣ηi∈B∑∂bl(i)(w,b)=b−∣B∣ηi∈B∑(w⊤x(i)+b−y(i)) (关于b的偏导)
批量大小和学习率的值通常是手动预先指定,而不是通过模型训练得到的。这些可以调整但不在训练过程中更新的参数称为超参数(hyperparameter)。调参(hyperparameter tuning)是选择超参数的过程。超参数通常是我们根据训练迭代结果来调整的,而训练迭代结果是在独立的验证数据集(validation dataset)上评估得到的。
在训练了预先确定的若干迭代次数后(或者直到满足某些其他停止条件后),我们记录下模型参数的估计值,表示为 w ^ , b ^ \hat{\mathbf{w}}, \hat{b} w^,b^。但是,即使我们的函数确实是线性的且无噪声,这些估计值也不会使损失函数真正地达到最小值。因为算法会使得损失向最小值缓慢收敛,但却不能在有限的步数内非常精确地达到最小值。
线性回归恰好是一个在整个域中只有一个最小值的学习问题,但是对像深度神经网络这样复杂的模型来说,损失平面上通常包含多个最小值。深度学习实践者很少会去花费大力气寻找这样一组参数,使得在训练集上的损失达到最小。事实上,更难做到的是找到一组参数,这组参数能够在我们从未见过的数据上实现较低的损失,这一挑战被称为泛化(generalization)。
3.1.1.5 Using Models for Prediction
给定特征估计目标的过程通常称为预测(prediction)或推断(inference)。但在统计学中,推断更多地表示基于数据集估计参数。
3.1.2 Vectorization Acceleration
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。为了实现这一点,需要我们对计算进行矢量化,从而利用线性代数库,而不是在Python中编写开销高昂的for循环,即使用:
n = 10000
a = torch.ones([n])
b = torch.ones([n])
c=a+b
而不是:
c = torch.zeros(n)
for i in range(n):c[i] = a[i] + b[i]
3.1.3 Normal Distribution and Squared Loss
噪声正态分布如下式:
y = w ⊤ x + b + ϵ , y = \mathbf{w}^\top \mathbf{x} + b + \epsilon, y=w⊤x+b+ϵ,
其中, ϵ ∼ N ( 0 , σ 2 ) \epsilon \sim \mathcal{N}(0, \sigma^2) ϵ∼N(0,σ2)。
因此,我们现在可以写出通过给定的 x \mathbf{x} x观测到特定 y y y的似然(likelihood):
P ( y ∣ x ) = 1 2 π σ 2 exp ( − 1 2 σ 2 ( y − w ⊤ x − b ) 2 ) . P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right). P(y∣x)=2πσ21exp(−2σ21(y−w⊤x−b)2).
现在,根据极大似然估计法,参数 w \mathbf{w} w和 b b b的最优值是使整个数据集的似然最大的值:
P ( y ∣ X ) = ∏ i = 1 n p ( y ( i ) ∣ x ( i ) ) . P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)}). P(y∣X)=i=1∏np(y(i)∣x(i)).
根据极大似然估计法选择的估计量称为极大似然估计量。虽然使许多指数函数的乘积最大化看起来很困难,但是我们可以在不改变目标的前提下,通过最大化似然对数来简化。由于历史原因,优化通常是说最小化而不是最大化。我们可以改为最小化负对数似然 − log P ( y ∣ X ) -\log P(\mathbf y \mid \mathbf X) −logP(y∣X)。由此可以得到的数学公式是:
− log P ( y ∣ X ) = ∑ i = 1 n 1 2 log ( 2 π σ 2 ) + 1 2 σ 2 ( y ( i ) − w ⊤ x ( i ) − b ) 2 . -\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2. −logP(y∣X)=i=1∑n21log(2πσ2)+2σ21(y(i)−w⊤x(i)−b)2.
现在我们只需要假设 σ \sigma σ是某个固定常数就可以忽略第一项,现在第二项除了常数 1 σ 2 \frac{1}{\sigma^2} σ21外,其余部分和前面介绍的均方误差是一样的。因此,在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。
3.1.4 From Linear Regression to Deep Networks
我们可以用描述神经网络的方式来描述线性模型,从而把线性模型看作一个神经网络。

首先,我们用“层”符号来重写这个模型。深度学习从业者喜欢绘制图表来可视化模型中正在发生的事情。我们将线性回归模型描述为一个神经网络。需要注意的是,该图只显示连接模式,即只显示每个输入如何连接到输出,隐去了权重和偏置的值。
在图中所示的神经网络中,输入为 x 1 , … , x d x_1, \ldots, x_d x1,…,xd,因此输入层中的输入数(或称为特征维度,feature dimensionality)为 d d d。网络的输出为 o 1 o_1 o1,因此输出层中的输出数是1。需要注意的是,输入值都是已经给定的,并且只有一个计算神经元。由于模型重点在发生计算的地方,所以通常我们在计算层数时不考虑输入层。也就是说,图中神经网络的层数为1。我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络,或称为单层神经网络。对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连,我们将这种变换( 图中的输出层)称为全连接层(fully-connected layer)或称为稠密层(dense layer)。
相关文章:

《动手学深度学习(PyTorch版)》笔记3.1
Chapter3 Linear Neural Networks 3.1 Linear Regression 3.1.1 Basic Concepts 我们通常使用 n n n来表示数据集中的样本数。对索引为 i i i的样本,其输入表示为 x ( i ) [ x 1 ( i ) , x 2 ( i ) , . . . , x n ( i ) ] ⊤ \mathbf{x}^{(i)} [x_1^{(i)}, x_2…...
【贪吃蛇:C语言实现】
文章目录 前言1.了解Win32API相关知识1.1什么是Win32API1.2设置控制台的大小、名称1.3控制台上的光标1.4 GetStdHandle(获得控制台信息)1.5 SetConsoleCursorPosition(设置光标位置)1.6 GetConsoleCursorInfo(获得光标…...
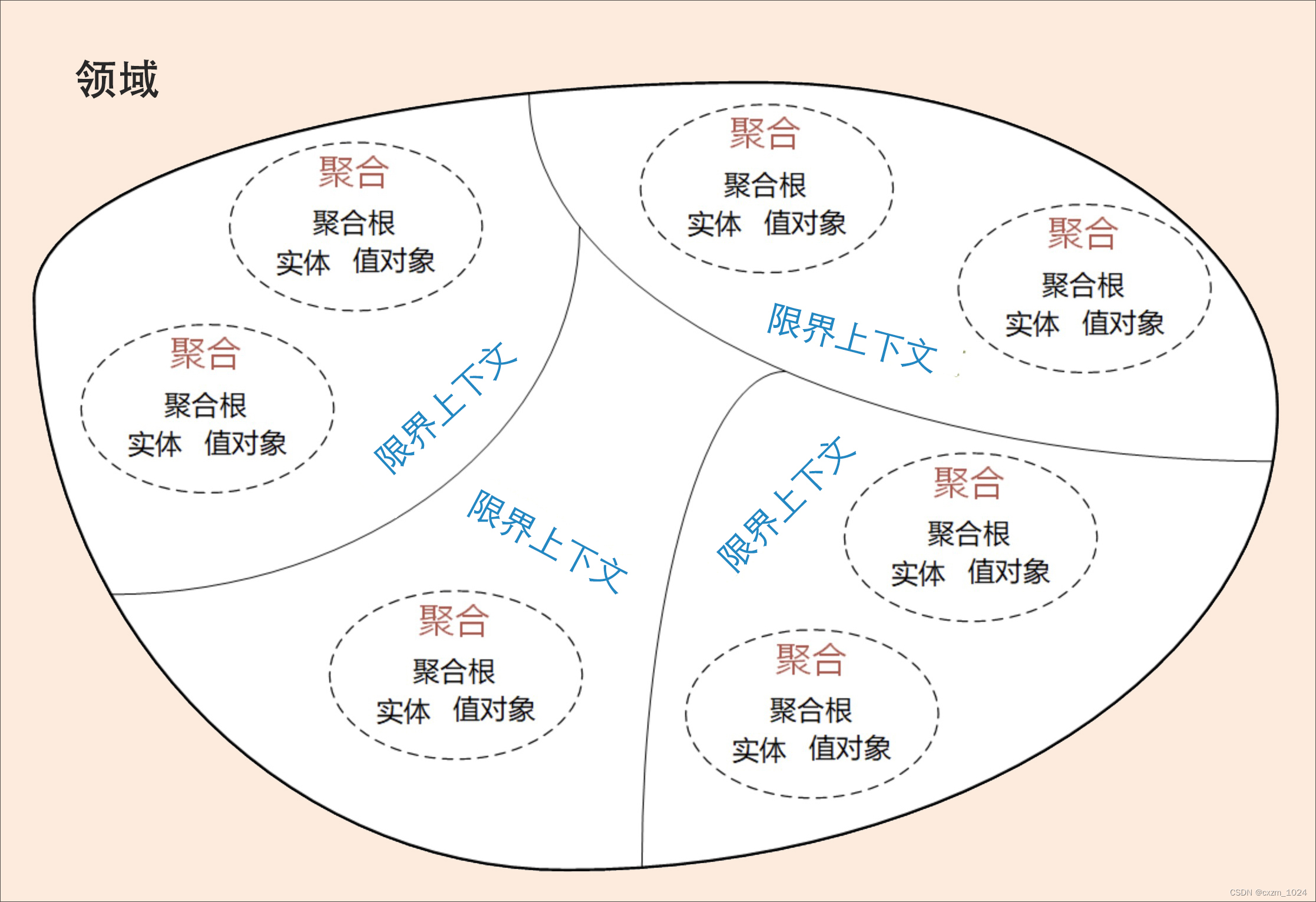
01.领域驱动设计:微服务设计为什么要选择DDD学习总结
目录 1、前言 2、软件架构模式的演进 3、微服务设计和拆分的困境 4、为什么 DDD适合微服务 5、DDD与微服务的关系 6、总结 1、前言 我们知道,微服务设计过程中往往会面临边界如何划定的问题,不同的人会根据自己对微服务的理 解而拆分出不同的微服…...
写静态页面——魅族导航_前端页面练习
0、效果: 1、html代码:: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><…...

Go 命令行解析 flag 包之快速上手
本篇文章是 Go 标准库 flag 包的快速上手篇。 概述 开发一个命令行工具,视复杂程度,一般要选择一个合适的命令行解析库,简单的需求用 Go 标准库 flag 就够了,flag 的使用非常简单。 当然,除了标准库 flag 外&#x…...
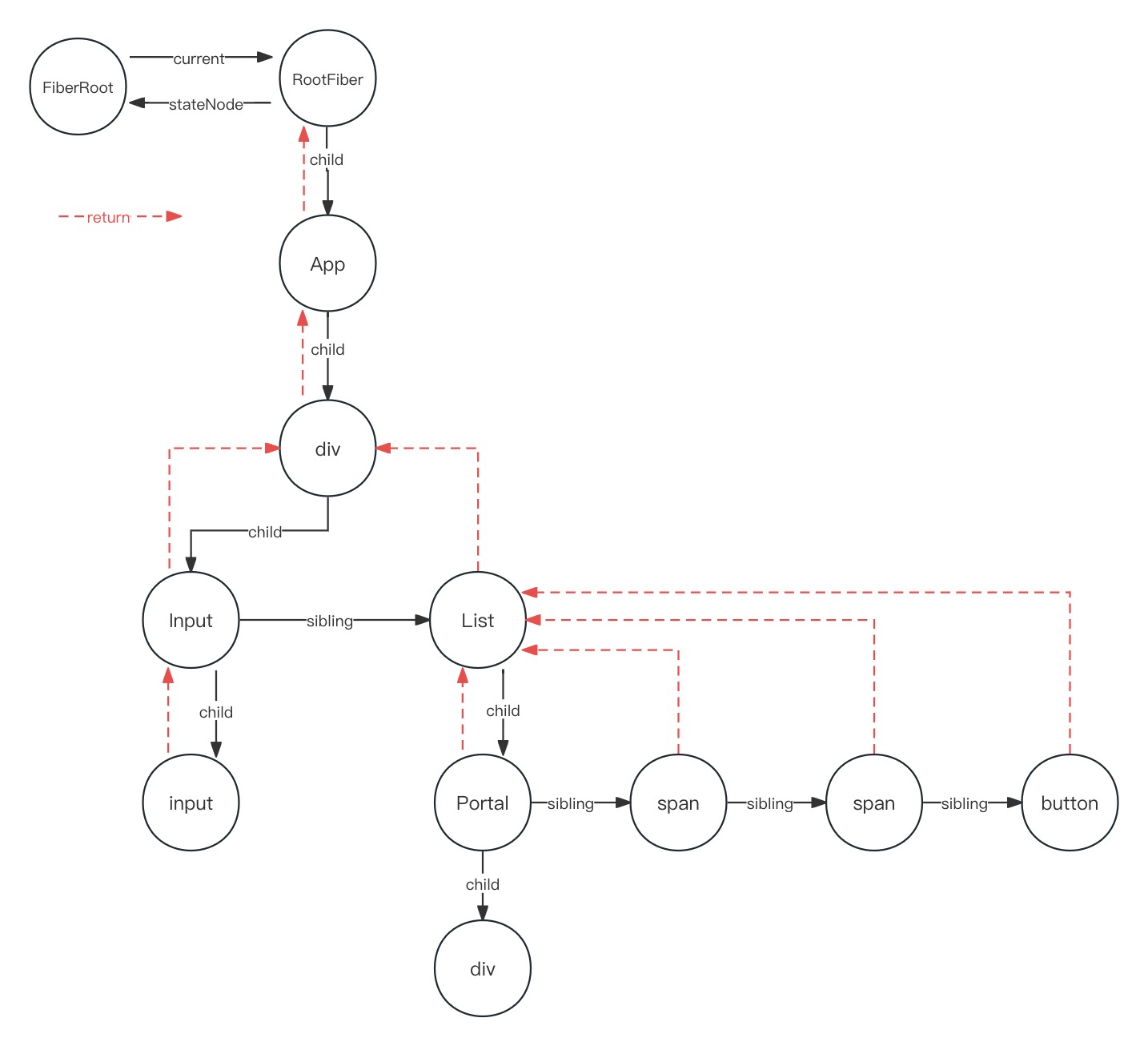
React16源码: React中commitAllHostEffects内部的commitDeletion的源码实现
commitDeletion 1 )概述 在 react commit 阶段的 commitRoot 第二个while循环中调用了 commitAllHostEffects,这个函数不仅仅处理了新增节点,更新节点最后一个操作,就是删除节点,就需要调用 commitDeletion࿰…...
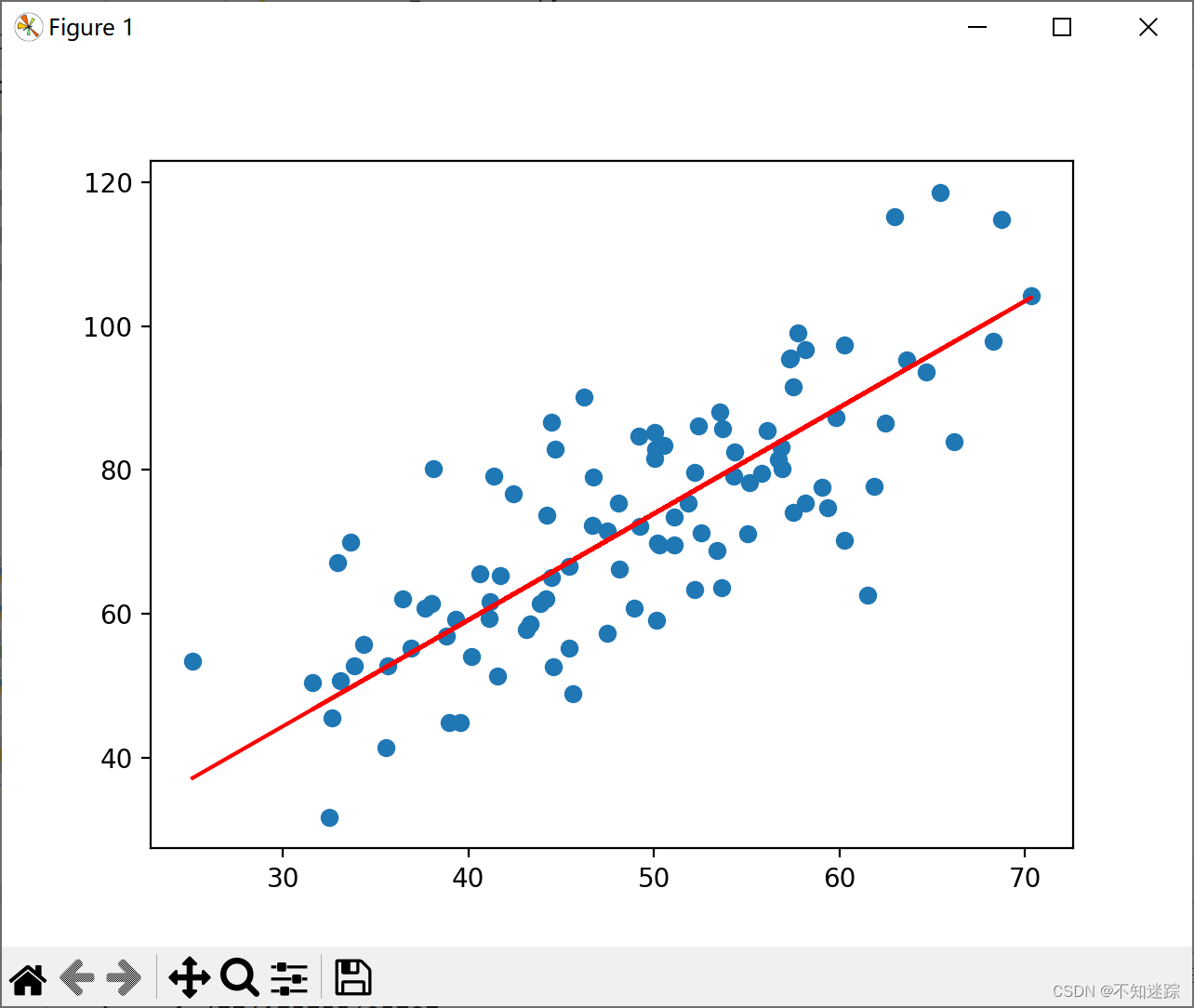
[机器学习]简单线性回归——梯度下降法
一.梯度下降法概念 2.代码实现 # 0. 引入依赖 import numpy as np import matplotlib.pyplot as plt# 1. 导入数据(data.csv) points np.genfromtxt(data.csv, delimiter,) points[0,0]# 提取points中的两列数据,分别作为x,y …...
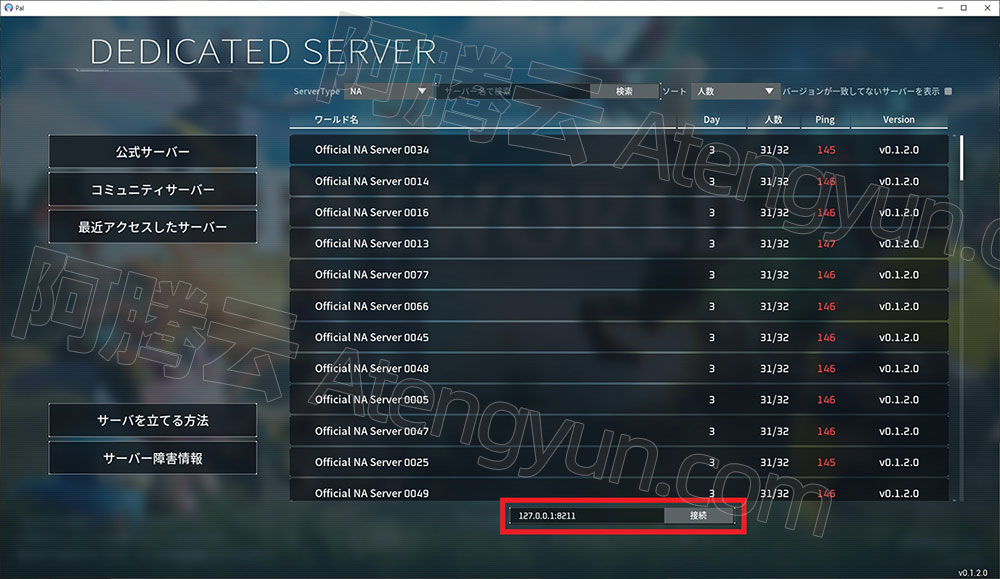
2024年搭建幻兽帕鲁服务器价格多少?如何自建Palworld?
自建幻兽帕鲁服务器租用价格表,2024阿里云推出专属幻兽帕鲁Palworld游戏优惠服务器,配置分为4核16G和4核32G服务器,4核16G配置32.25元/1个月、3M带宽96.75元/1个月、8核32G配置10M带宽90.60元/1个月,8核32G配置3个月271.80元。ECS…...
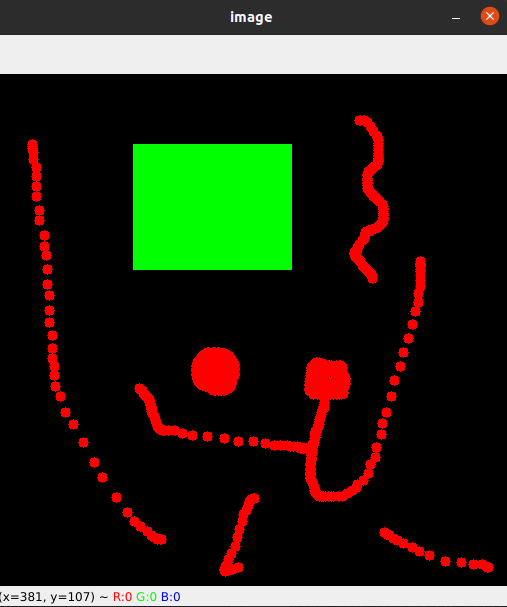
『OpenCV-Python|鼠标作画笔』
Opencv-Python教程链接:https://opencv-python-tutorials.readthedocs.io/ 本文主要介绍OpenCV-Python如何将鼠标作画笔绘制圆或者矩形。 示例一:图片上双击的位置绘制一个圆圈 首先创建一个鼠标事件回调函数,鼠标事件发生时就会被执行。鼠标…...

关于如何利用ChatGPT提高编程效率的
自从去年ChatGPT3.5推出以后,这一年时间在编程过程中我也在慢慢熟悉人工智能的使用,目前来看即使是免费的ChatGPT3.5对于编程效率的提升也是有很大帮助的,虽然在使用过程中确实出现了一些问题,本文记录下我的一些心得体会和用法。…...

Excel VBA ——从MySQL数据库中导出一个报表-笔记
本文主要涉及: VBA中数据库连接参数改成从配置文件获取 VBA连接MySQL数据库 VBA读MySQL数据库 演示两种写入工作簿的代码实现系统环境: Windows 10 64bit Excel 365 64bit WAMP(3.2.2.2 64bit)集成的MariaDB版本为10.4.10&#…...

金融OCR领域实习日志(一)——OCR技术从0到1全面调研
一、OCR基础 任务要求: 工作原理 OCR(Optical Character Recognition,光学字符识别)是指电子设备(例如扫描仪或数码相)检查纸上打印的字符,经过检测暗、亮的模式肯定其形状,而后用…...
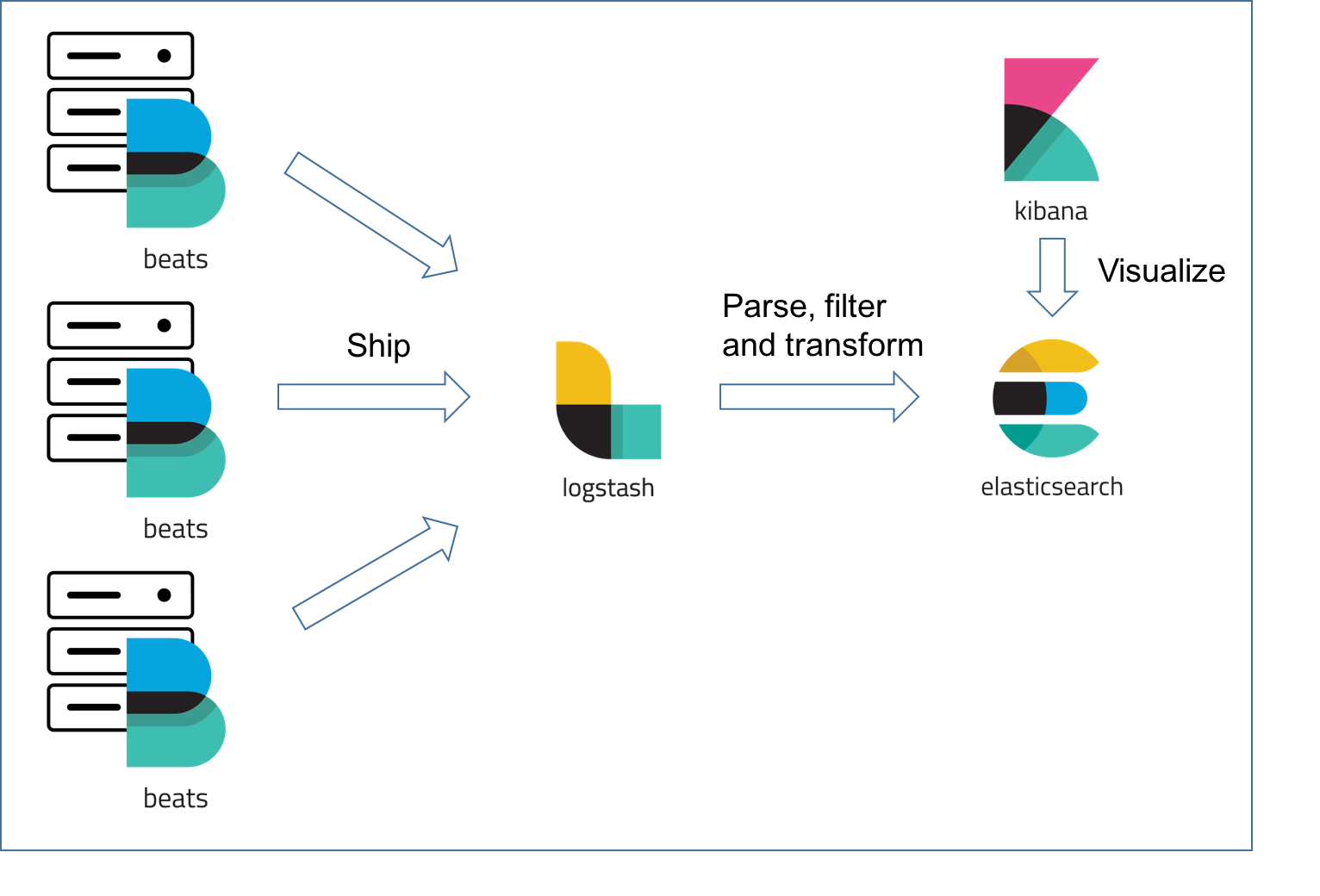
ELK日志解决方案
ELK日志解决方案 ELK套件日志系统应该是Elasticsearch使用最广泛的场景之一了,Elasticsearch支持海量数据的存储和查询,特别适合日志搜索场景。广泛使用的ELK套件(Elasticsearch、Logstash、Kibana)是日志系统最经典的案例,使用Logstash和Be…...

嵌入式学习-驱动
嵌入式的一些基本概念 CPU与MCU的区别 CPU(中央处理器,central processing unit) 指集成了运算器、控制器、寄存器、高速缓存等功能模块的芯片,负责执行计算机程序指令的处理器。MCU(单片微型计算机或单片机,microco…...

系统架构17 - 软件工程(5)
软件工程 软件测试测试原则测试方法静态测试动态测试黑盒测试白盒测试灰盒测试自动化测试 测试阶段单元测试集成测试系统测试性能测试验收测试其它测试AB测试Web测试链接测试表单测试 测试用例设计黑盒测试用例白盒测试用例 调试 系统维护遗留系统系统转换转换方式数据转换与迁…...
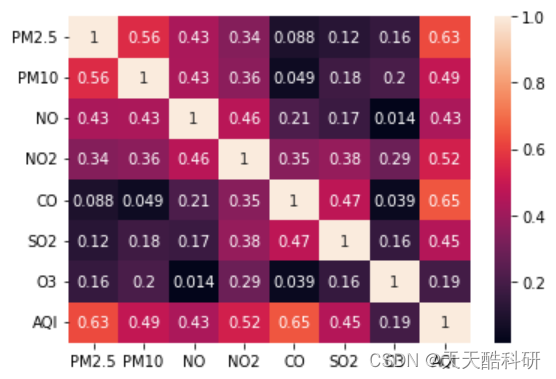
空气质量预测 | Python实现基于线性回归、Lasso回归、岭回归、决策树回归的空气质量预测模型
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 政府机构使用空气质量指数 (AQI) 向公众传达当前空气污染程度或预测空气污染程度。 随着 AQI 的上升,公共卫生风险也会增加。 不同国家有自己的空气质量指数,对应不同国家的空气质量标准。 对于空气质量预测,…...

MYSQL数据库基本操作-DQL-基本查询
一.概念 数据库管理系统一个重要功能就是数据查询。数据查询不应是简单返回数据库中存储的数据,还应该根据需要对数据进行筛选以及确定数据以什么样的格式显示。 MySQL提供了功能强大,灵活的语句来实现这些操作。 MySQL数据库使用select语句来查询数据…...

gdb 调试 - 在vscode图形化展示在远程的gdb debug过程
前言 本地机器的操作系统是windows,远程机器的操作系统是linux,开发在远程机器完成,本地只能通过ssh登录到远程。现在目的是要在本地进行图形化展示在远程的gdb debug过程。(注意这并不是gdb remote !!&am…...
Android 13.0 SystemUI下拉状态栏定制二 锁屏页面横竖屏时钟都居中功能实现二
1.前言 在13.0的系统rom定制化开发中,在关于systemui的锁屏页面功能定制中,由于在平板横屏锁屏功能中,时钟显示的很大,并且是在左旁边居中显示的, 由于需要和竖屏显示一样,所以就需要用到小时钟显示,然后同样需要居中,所以就来分析下相关的源码,来实现具体的功能 如图…...
docker 部署xxl-job
docker 部署xxl-job XXL-JOB github地址 https://github.com/xuxueli/xxl-job XXL-JOB 文档地址 https://www.xuxueli.com/xxl-job/ XXL-JOB是一个分布式任务调度平台,其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
