[足式机器人]Part3 机构运动学与动力学分析与建模 Ch01-1 刚体系统的运动学约束
本文仅供学习使用,总结很多本现有讲述运动学或动力学书籍后的总结,从矢量的角度进行分析,方法比较传统,但更易理解,并且现有的看似抽象方法,两者本质上并无不同。
2024年底本人学位论文发表后方可摘抄
若有帮助请引用
本文参考:
《空间机构的分析与综合(上册)》-张启先,感谢张启先先生对机构学的卓越贡献,希望下册有见天明之日!
《高等机构学》-白师贤
《高等空间机构学》-黄真
《机构运动微分几何学分析与综合》-王德伦
食用方法
自由度?约束——本质含义是什么?如何表达?
系统的自由度?广义坐标的自由度?
如何表示约束方程?
务必自己计算自由度,了解约束的含义
机构运动学与动力学分析与建模 Ch00-1-1 刚体系统的运动学约束
- 1. 广义坐标与约束
- 1.1 参考坐标
- 1.2 约束
- 2. 系统自由度计算
- 2.1 空间开式运动链的自由度公式及末杆的自由度分析
- 2.1.1 空间开式运动链的自由度公式
- 2.1.2 空间开式运动链的末杆的自由度分析
- 2.1.3 总结——常用判断方法
- 2.2 空间单封闭形机构
- 2.2.1 空间单封闭形机构的自由度公式
- 2.2.2 空间单封闭形机构的自由度计算
- 2.2.2.1 闭合约束数的确定和过约束机构的特点
- 2.2.2.2 局部自由度的确定
- 2.2.2.3 消极自由度的考虑
- 2.2.3 空间多封闭形机构
- 2.2.3.1 独立的封闭形
- 2.2.3.2 空间多封闭形机构的自由度计算
- 2.3 几个例子
- 2.3.1 螺旋机构
1. 广义坐标与约束
1.1 参考坐标
根据上述章节的学习,我们知道:
- 空间中对某一
点的表述,需要3个位姿参数(比如点的坐标)——即需要3个约束方程; - 空间中对某一
矢量的表述,需要2个位姿参数(比如球坐标系下的两个角度值)——即需要2个约束方程; - 空间中对某一
直线的表述,需要5个位姿参数(给定点+给定矢量)——即需要5个约束方程; - 空间中对某一
平面的表述,需要4个位姿数(给定矢量+矢量方向上的位置)——即需要4个约束方程; - 空间中对某一
刚体的表述,需要6个位姿参数(给定点+矢量方向+沿矢量方向的转角)——即需要6个约束方程;
这些例子对于我们理解运动副有很大的作用
而对于刚体系统而言,其运动坐标系的参考坐标具体表示,与所选择的表示方法有关:用符号 q ⃗ Σ M F \vec{q}_{\varSigma _{\mathrm{M}}}^{F} qΣMF来表示刚体 Σ M \varSigma _{\mathrm{M}} ΣM在坐标系 { F } \left\{ F \right\} {F}下的广义坐标参数。展开可写为:
q ⃗ Σ M F = [ R ⃗ Σ M F θ ⃗ Σ M F ] \vec{q}_{\varSigma _{\mathrm{M}}}^{F}=\left[ \begin{array}{c} \vec{R}_{\varSigma _{\mathrm{M}}}^{F}\\ \vec{\theta}_{\varSigma _{\mathrm{M}}}^{F}\\ \end{array} \right] qΣMF=[RΣMFθΣMF]
其中: R ⃗ Σ M F \vec{R}_{\varSigma _{\mathrm{M}}}^{F} RΣMF表示体坐标系 { M } \left\{ M \right\} {M}在固定坐标系 { F } \left\{ F \right\} {F}下的位置参数, θ ⃗ Σ M F \vec{\theta}_{\varSigma _{\mathrm{M}}}^{F} θΣMF表示刚体的姿态参数(欧拉角,四元数,罗德里格斯参数等),对于不同的表达方式, q ⃗ Σ M F \vec{q}_{\varSigma _{\mathrm{M}}}^{F} qΣMF有不同的维数。
1.2 约束
若一个系统由多个刚体之间的相互作用组成(存在运动副连接),此时该系统中每个单独刚体的运动,都会受到其他部分的影响——确立一组相互独立的广义坐标(即自由度——此时的自由度表示为所需的广义坐标数量,即需要几个自由度才能完整的描述该系统各个构件状态),运动学约束即上述的约束方程,几个约束方程即限制了几个自由度。
对于一个多体系统而言,其广义坐标的数目为 n n n,这些刚体之间存在 n c n_{\mathrm{c}} nc个约束方程
若能将约束方程写成如下的矩阵形式:
C ( q ⃗ , t ) = [ C 1 ( q ⃗ , t ) C 2 ( q ⃗ , t ) ⋮ C n c ( q ⃗ , t ) ] = C ( q ⃗ 1 , q ⃗ 2 , ⋯ , q ⃗ n , t ) \boldsymbol{C}\left( \vec{\boldsymbol{q}},t \right) =\left[ \begin{array}{c} C_1\left( \vec{\boldsymbol{q}},t \right)\\ C_2\left( \vec{\boldsymbol{q}},t \right)\\ \vdots\\ C_{\mathrm{n}_{\mathrm{c}}}\left( \vec{\boldsymbol{q}},t \right)\\ \end{array} \right] =\boldsymbol{C}\left( \vec{q}_1,\vec{q}_2,\cdots ,\vec{q}_{\mathrm{n}},t \right) C(q,t)= C1(q,t)C2(q,t)⋮Cnc(q,t) =C(q1,q2,⋯,
相关文章:

[足式机器人]Part3 机构运动学与动力学分析与建模 Ch01-1 刚体系统的运动学约束
本文仅供学习使用,总结很多本现有讲述运动学或动力学书籍后的总结,从矢量的角度进行分析,方法比较传统,但更易理解,并且现有的看似抽象方法,两者本质上并无不同。 2024年底本人学位论文发表后方可摘抄 若有帮助请引用 本文参考: 《空间机构的分析与综合(上册)》-张启先…...

51单片机智能小车
51单片机智能小车 delay.c #include "intrins.h"void Delay2000ms() //11.0592MHz {unsigned char i, j, k;i 15;j 2;k 235;do{do{while (--k);} while (--j);} while (--i); }void Delay10us() //11.0592MHz {unsigned char i;i 2;while (--i); }void Delay…...

9. 嵌入式系统开发:安全性与可靠性设计模式---引言
在复杂的嵌入式系统设计中,为了提高嵌入式系统安全性并保护嵌入式系统免受各种潜在故障的影响,可以采用不同的设计模式。这些模式各自有优势和适用的场景: 1. 受保护的单通道模式(Protected Single Channel Pattern) …...
内网安全:Exchange服务
目录 Exchange服务 实验环境 域横向移动-内网服务-Exchange探针 一. 端口扫描 二. SPN扫描 三. 脚本探针(还可以探针是否有安全漏洞) 域横向移动-内网服务-Exchange爆破 一 .BurpSuite Intruder模块爆破 域横向移动-内网服务-Exchange漏洞 CVE-2020-17144 Exchange R…...

Flask介绍和优势
Flask诞生于2010年,是由Armin Ronacher用Python语言编写的一款轻量级Web开发框架。自发布以来,Flask逐渐成为开发人员喜爱的选择,并在2021年5月发布了Flask 2.0版本,引入了一些新增特性,如基本的异步支持。 使用Flask…...

喜报|「云原生数据库PolarDB」、「阿里云瑶池一站式数据管理平台」揽获“2023技术卓越奖”
日前,国内知名IT垂直媒体&技术社区IT168公布2023年“技术卓越奖”评选结果,经由行业CIO/CTO大咖、技术专家及IT媒体三方的联合严格评审,阿里云瑶池数据库揽获两项大奖:云原生数据库PolarDB荣获“2023年度技术卓越奖”…...

【动态规划】【字符串】【行程码】1531. 压缩字符串
作者推荐 视频算法专题 本文涉及知识点 动态规划汇总 LeetCode 1531. 压缩字符串 II 行程长度编码 是一种常用的字符串压缩方法,它将连续的相同字符(重复 2 次或更多次)替换为字符和表示字符计数的数字(行程长度)…...

检测头篇 | 原创自研 | YOLOv8 更换 SEResNeXtBottleneck 头 | 附详细结构图
左图:ResNet 的一个模块。右图:复杂度大致相同的 ResNeXt 模块,基数(cardinality)为32。图中的一层表示为(输入通道数,滤波器大小,输出通道数)。 1. 思路 ResNeXt是微软研究院在2017年发表的成果。它的设计灵感来自于经典的ResNet模型,但ResNeXt有个特别之处:它采用…...
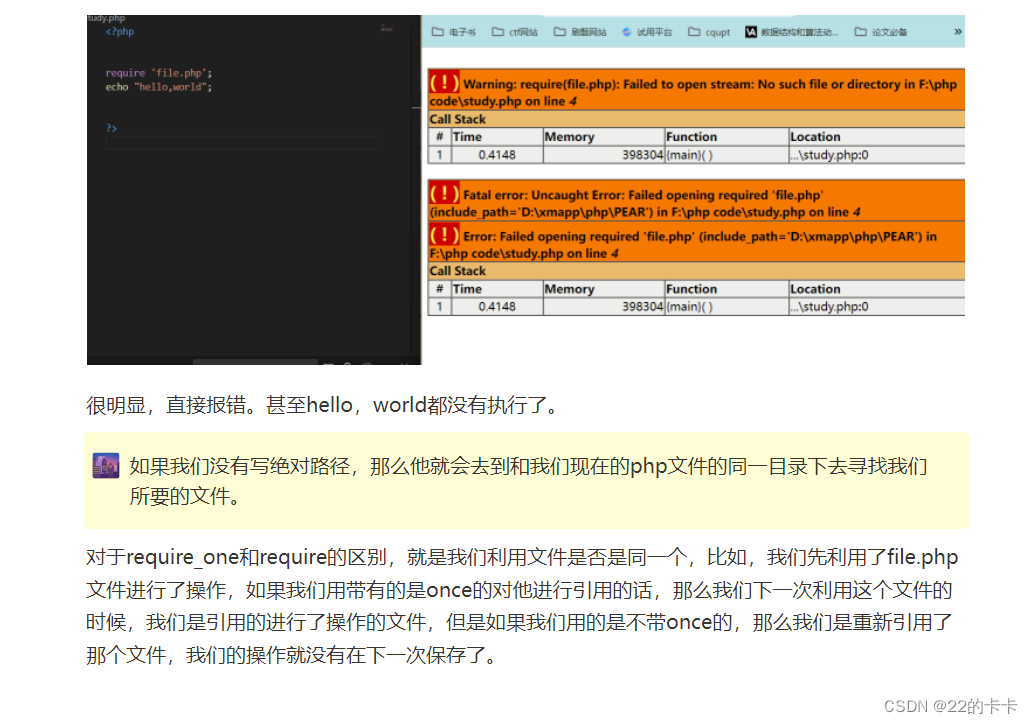
PHP语法
#本来是在学命令执行,所以学了学,后来发现,PHP语法和命令执行的关系好像没有那么大,不如直接学php的一些命令执行函数了。# #但是还是更一下,毕竟还是很多地方都要求掌握php作为脚本语言,所以就学了前面的…...
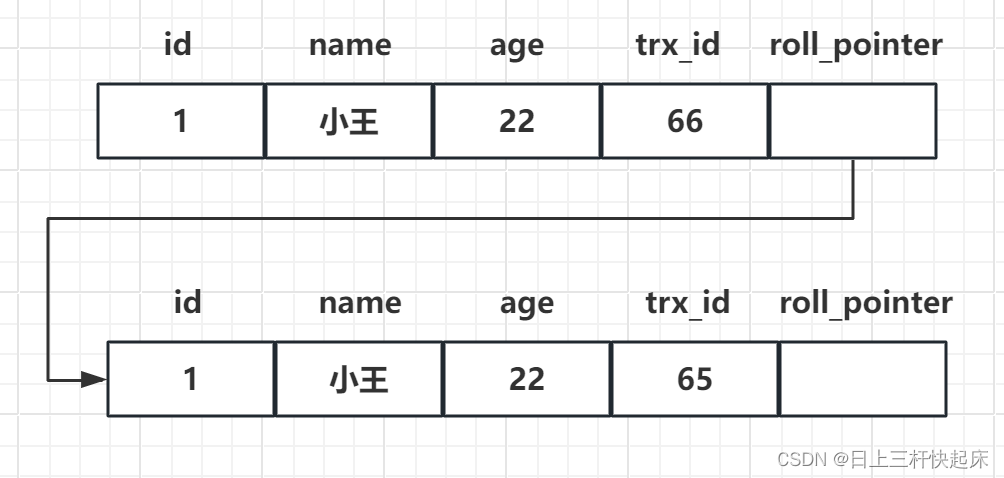
MySQL:三大日志(binlog、redolog、undolog)
再了解三个日志前我们先了解一下MySQL的两层架构: Server 层负责建立连接、分析和执行 SQL。MySQL 大多数的核心功能模块都在这实现,主要包括连接器,查询缓存、解析器、预处理器、优化器、执行器等。另外,所有的内置函数和所有跨…...

【QT+QGIS跨平台编译】之十二:【libpng+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文件目录 一、libpng介绍二、文件下载三、文件分析四、pro文件五、编译实践一、libpng介绍 PNG(Portable Network Graphics,便携式网络图形),是一种采用无损压缩算法的位图格式,支持索引、灰度、RGB三种颜色方案以及Alpha通道等特性。 PNG使用从LZ77派生的无损数据压缩算…...
Windows 和 Anolis 通过 Docker 安装 Milvus 2.3.4
Windows 10 通过 Docker 安装 Milvus 2.3.4 一.Windows 安装 Docker二.Milvus 下载1.下载2.安装1.Windows 下安装(指定好Docker文件目录)2.Anolis下安装 三.数据库访问1.ATTU 客户端下载 一.Windows 安装 Docker Docker 下载 双击安装即可,安…...
)
JUC并发编程与源码分析学习笔记(三)
目录 五十六、JMM之入门简介 五十七、JMM之学术定义和作用 五十八、JMM之三大特性 五十九、JMM之多线程对变量的读写过程 六十、JMM之happens-before-上集 六十一、JMM之happens-before-下集 五十六、JMM之入门简介 Java内存模型之JMM 1、先从大厂面试题开始 ①、你知道…...
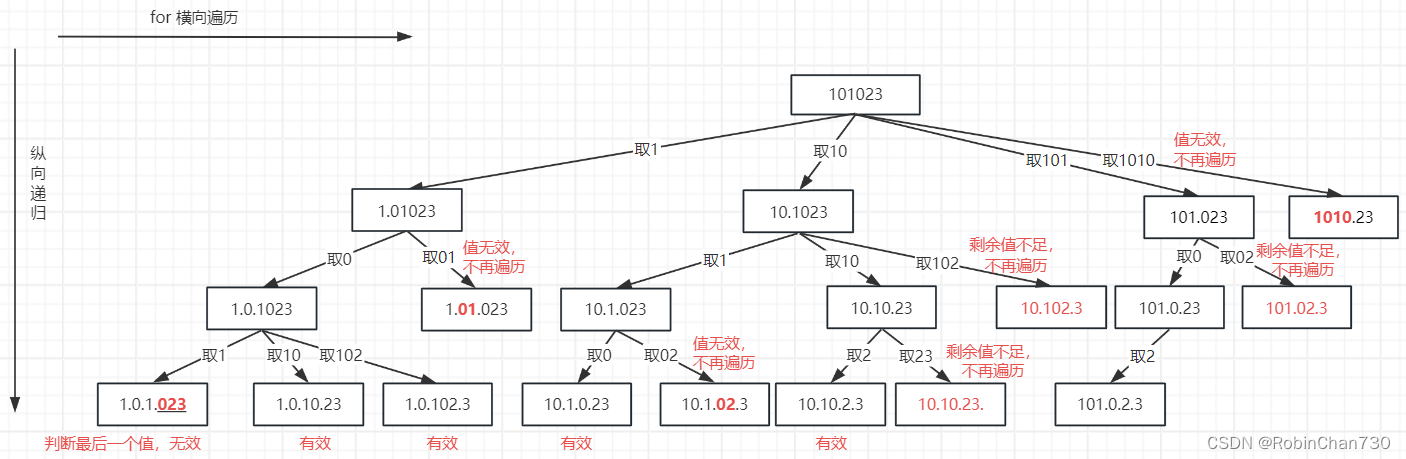
力扣日记1.28-【回溯算法篇】93. 复原 IP 地址
力扣日记:【回溯算法篇】93. 复原 IP 地址 日期:2023.1.28 参考:代码随想录、力扣 93. 复原 IP 地址 题目描述 难度:中等 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0&…...

Java 的反射学习总结
目录 一、什么是反射? 二、如何获取类对象? 三、如何通过类对象来创建类的对象? 四、类对象获取类构造器的方式 五、通过类对象获取类的属性 六、通过类对象获取类的方法 一、什么是反射? 反射是指在运行时动态地获取、检查…...

图论第二天|695. 岛屿的最大面积 1020. 飞地的数量 130. 被围绕的区域 417. 太平洋大西洋水流问题 827.最大人工岛
目录 Leetcode695. 岛屿的最大面积Leetcode1020. 飞地的数量Leetcode130. 被围绕的区域Leetcode417. 太平洋大西洋水流问题Leetcode827.最大人工岛 Leetcode695. 岛屿的最大面积 文章链接:代码随想录 题目链接:695. 岛屿的最大面积 思路:dfs …...
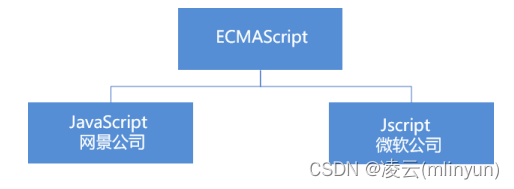
【JavaScript 基础入门】02 JavaScrip 详细介绍
JavaScrip 详细介绍 目录 JavaScrip 详细介绍1. JavaScript 是什么2. JavaScript的作用3. HTML/CSS/JS 的关系4. 浏览器执行 JS 简介5. JavaScript 的组成6. JavaScript 的特点 1. JavaScript 是什么 JavaScript,通常缩写为 JS,是一种高级的,…...
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之CheckboxGroup组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之CheckboxGroup组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、CheckboxGroup组件 提供多选框组件,通常用于某选项的打开或关…...

【极数系列】Flink配置参数如何获取?(06)
文章目录 gitee码云地址简介概述01 配置值来自.properties文件1.通过路径读取2.通过文件流读取3.通过IO流读取 02 配置值来自命令行03 配置来自系统属性04 注册以及使用全局变量05 Flink获取参数值Demo1.项目结构2.pom.xml文件如下3.配置文件4.项目主类5.运行查看相关日志 gite…...
【docker】linux系统docker的安装及使用
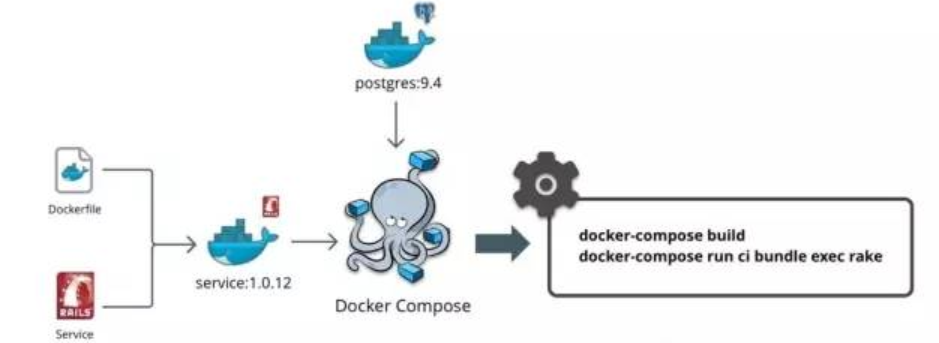
一、docker应用的安装 1.1 安装方式 Docker的自动化安装,即使用提供的一键安装的脚本,进行安装。 官方的一键安装方式:curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun 国内 daocloud一键安装命令:curl -s…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
