【动态规划】【字符串】【行程码】1531. 压缩字符串
作者推荐
视频算法专题
本文涉及知识点
动态规划汇总
LeetCode 1531. 压缩字符串 II
行程长度编码 是一种常用的字符串压缩方法,它将连续的相同字符(重复 2 次或更多次)替换为字符和表示字符计数的数字(行程长度)。例如,用此方法压缩字符串 “aabccc” ,将 “aa” 替换为 “a2” ,“ccc” 替换为` “c3” 。因此压缩后的字符串变为 “a2bc3” 。
注意,本问题中,压缩时没有在单个字符后附加计数 ‘1’ 。
给你一个字符串 s 和一个整数 k 。你需要从字符串 s 中删除最多 k 个字符,以使 s 的行程长度编码长度最小。
请你返回删除最多 k 个字符后,s 行程长度编码的最小长度 。
示例 1:
输入:s = “aaabcccd”, k = 2
输出:4
解释:在不删除任何内容的情况下,压缩后的字符串是 “a3bc3d” ,长度为 6 。最优的方案是删除 ‘b’ 和 ‘d’,这样一来,压缩后的字符串为 “a3c3” ,长度是 4 。
示例 2:
输入:s = “aabbaa”, k = 2
输出:2
解释:如果删去两个 ‘b’ 字符,那么压缩后的字符串是长度为 2 的 “a4” 。
示例 3:
输入:s = “aaaaaaaaaaa”, k = 0
输出:3
解释:由于 k 等于 0 ,不能删去任何字符。压缩后的字符串是 “a11” ,长度为 3 。
提示:
1 <= s.length <= 100
0 <= k <= s.length
s 仅包含小写英文字母
动态规划
预处理
将s转成arr,每个元素是{字符,长度}。
比如:aabbaa变成{{‘a’,2},{'b",2},{‘a’,2}}
长度0,表示0个字符。长度1,表示1个字符。长度2,表示2到9.长度3,表示10到99,长度4,表示100及以上。
动态规划的状态表示
pre[j] 表示处理完arr[0,i)后, 用去j个字符的最短行程码。
dp[j] 表示处理完arr[0,i]后, 用去j个字符的最短行程码。
pre2[ch][j][m] 表示处理完arr[0,i)后,,以ch+'a’结尾,用去j个字符,最后有m个ch的最短行程码。
dp2表示处理完arr[0,i]…
动态规划的转移方程
arr[i]没有和前面的元素合并:
枚举j,枚举减少长度:0、1、2、3、4
arr[j]和前面的合并:
枚举j,m 再枚举减少长度:0、1、2、3 、4
合并示例:aa d d ‾ \underline{dd} ddaa 删除dd后,就是4个aa了。
动态规划的初始状态
pre[0]=0,其它100。
pre2全部100。
动态规划的填表顺序
i从小到大。
动态规划的返回值
pre.back().back()
代码
核心代码
class Solution {
public:int getLengthOfOptimalCompression(string s, int k) {const int lenArr = s.length();vector<pair<char, int>> arr;for (int left = 0, i = 0; i <= s.length(); i++){if ((i >= s.length()) || (s[left] != s[i])){arr.emplace_back(s[left], i - left);left = i;}}vector<int> vLen = { 0,1,2,10,100 };auto GetCodeLen = [&vLen](int len){int i = vLen.size() - 1;for (; (i >= 0) && (len < vLen[i]); i--);return i;};auto MaxLen = [&vLen](int len){return vLen[len + 1] - 1;};vector<int> pre(lenArr + 1, 100);pre[0] = 0;vector<vector<vector<int>>> dp3(26, vector<vector<int>>(lenArr+1, vector<int>(lenArr + 1, 100)));for (const auto& [ch, cnt] : arr){vector<int> dp(lenArr + 1, 100);auto& dp2 = dp3[ch - 'a'];auto pre2 = dp2;auto Update = [&lenArr,&dp,&dp2](int j, int iCodeLen,const char& chEnd,int iEndLen){if (j > lenArr){return;}dp[j] = min(dp[j], iCodeLen);if (iEndLen <= lenArr){dp2[j][iEndLen] = min(dp2[j][iEndLen], iCodeLen);}}; //处理没合并for (int j = 0; j <= lenArr; j++){ const int curCodeLen = GetCodeLen(cnt);Update(j + cnt, pre[j] + curCodeLen,ch,cnt);for (int curCodeLen2 = curCodeLen - 1; curCodeLen2 >= 0; curCodeLen2--){//处理 行程妈缩短1,2...Update(j + MaxLen(curCodeLen2), pre[j] + curCodeLen2,ch, MaxLen(curCodeLen2));}}for (int j = 0; j <= lenArr; j++){for (int m = 0; m <= j; m++){const int curCodeLen = GetCodeLen(cnt+m );Update(j + cnt, pre2[j][m] - GetCodeLen(m) + GetCodeLen(m + cnt), ch, m + cnt);for (int curCodeLen2 = curCodeLen - 1; curCodeLen2 >= 0; curCodeLen2--){//处理 行程妈缩短1,2...Update(j -m + MaxLen(curCodeLen2), pre2[j][m] - GetCodeLen(m) + curCodeLen2,ch, MaxLen(curCodeLen2));}}}pre.swap(dp); }return *std::min_element(pre.begin() + pre.size() - k-1, pre.end());}
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{ string s;int k;{Solution sln;s = "aaa", k = 2;auto res = sln.getLengthOfOptimalCompression(s, k);Assert(1, res);}{Solution sln;s = "aaab", k = 2;auto res = sln.getLengthOfOptimalCompression(s, k);Assert(2, res);}{Solution sln;s = "aaabcccd", k = 2;auto res = sln.getLengthOfOptimalCompression(s, k);Assert(4, res);}{Solution sln;s = "aabbaa", k = 2;auto res = sln.getLengthOfOptimalCompression(s, k);Assert(2, res);}{Solution sln;s = "aaaaaaaaaaa", k = 0;auto res = sln.getLengthOfOptimalCompression(s, k);Assert(3, res);}{Solution sln;s = "spnskpulpsiqagreoajsltdrdlnpsdqapmsdlnlirasgfijafeoqjnddpaifsqpghshclqummgootsmkcgneofrkboirkplqijoi", k = 25;auto res = sln.getLengthOfOptimalCompression(s, k);Assert(3, res);}}
动态规划优化
前一个解法的空间复杂度在过与不过的边缘。
动态规划的状态表示
dp[i][j] 表示处理了arr[0,i),选择了j个字符的最短行程码。
动态规划的转移方程
分两种情况: 和前面的项目合并,和前面的项不合并。细节同上。
动态规划的初始值
dp[0][0]=0,其它100。
动态规划的填表顺序
i从小到大,j从小到大。
动态规划的返回值
dp.back的后k+1个元素的最小值。
优化后的代码
class Solution {
public:int getLengthOfOptimalCompression(string s, int k) {const int lenArr = s.length();vector<pair<char, int>> arr;for (int left = 0, i = 0; i <= s.length(); i++){if ((i >= s.length()) || (s[left] != s[i])){arr.emplace_back(s[left], i - left);left = i;}}vector<int> vLen = { 0,1,2,10,100 };auto GetCodeLen = [&vLen](int len){int i = vLen.size() - 1;for (; (i >= 0) && (len < vLen[i]); i--);return i;};auto MaxLen = [&vLen](int len){return vLen[len + 1] - 1;};vector<vector<int>> dp(arr.size() + 1, vector<int>(lenArr + 1, 100));dp[0][0] = 0;int i = -1;for (const auto& [ch, cnt] : arr){i++;auto& pre = dp[i];auto& cur = dp[i + 1];auto Update = [&lenArr, &cur](int j, int iCodeLen){if (j > lenArr){return;}cur[j] = min(cur[j], iCodeLen);};//处理没合并for (int j = 0; j <= lenArr; j++){const int curCodeLen = GetCodeLen(cnt);Update(j + cnt, pre[j] + curCodeLen);for (int curCodeLen2 = curCodeLen - 1; curCodeLen2 >= 0; curCodeLen2--){//处理 行程妈缩短1,2...Update(j + MaxLen(curCodeLen2), pre[j] + curCodeLen2);}}int cnt2 = 0;for (int m = i ; m >= 0; m--){if (arr[m].first != ch){continue;}cnt2 += arr[m].second;//合并后的字符数 const int curCodeLen = GetCodeLen(cnt2);for (int j = 0; j <= lenArr; j++){Update(j + cnt2, dp[m][j] + curCodeLen);for (int curCodeLen2 = curCodeLen - 1; curCodeLen2 >= 0; curCodeLen2--){//处理 行程妈缩短1,2...Update(j + MaxLen(curCodeLen2), dp[m][j] + curCodeLen2);}}} }return *std::min_element(dp.back().begin() + dp.back().size() - k - 1, dp.back().end());}
};
动态规划三
arr数组,少许提升性能,但增加了复杂度,不采用。
动态规划的状态
dp[i][j]表示 从s[0,i)中删除j个字符 最短的行程码。
动态规划的转移方程
令x = dp[i+1][j]
情况一:删除s[i+1]
那x等于dp[i][j-1] 公式一
情况二:不删除,且可能和前面的字符结合后,删除。
不市一般性,令s[i]=‘a’,且它的前面只有三个’a’,小标分别为i1,i2,i3。
情况a:
s[i]没有和其它’a’结合,则x= dp[i][j]+GetCodeLen (1)。 公式二
情况b:
s[i]和s[i3]结合,s(i3,i)之间非’a’的数量为diff,全部删除。
b1: i和i3 都没删除。 x = dp[i3][j-diff] + GetCodeLen(2) → \rightarrow → dp[i-diff-1][j-diff] + GetCodeLen(2) 公式三
b2: i3删除。x = dp[i3][j-diff-1] + GetCodeLen(1) → \rightarrow → dp[i-diff-1][j-diff-1] + GetCodeLen(1) 就是公式二和公式一结合。
情况c:
s[i]和s[i2] s[i3]结合: s(i2,i)之间非’a’的数量为diff2,全部删除。
c1,不删除’a’。 dp[i2][j-diff2] + GetCodeLen(3) ** 公式四**
c2,删除一个’a’ dp[i2][j-diff2-1] + GetCodeLen(2) → \rightarrow → dp[i-diff2-2][j-diff2-1]+GetCodeLen(2) 就是公式三和公式的结合,不需要枚举。
c3 删除两个’a’。dp[i-diff2-2][j-diff2-2] + GetCodeLen(1) 就是公式二和公式一结合,不用枚举。
总结:
无论多少个字符结合,全删除就是公式一。
保留一个就是公式二。
保留三个就是公式三。
…
m个字符结合,只需要枚举m个字符,mm个字符(mm < m )枚举mm个字符结合的时候考虑。
可以这样理解:
m个字符合并后,删除m-mm个,保留mm个。 保留任意mm个都一样,那保留后mm个。所以只需要枚举:保留后mm个。
动态规划的初始值
dp[0][0] = 0,其它100。
动态规划的填表顺序
i从小到大。
动态规划的返回值
dp.back()的最小值。
代码
class Solution {
public:int getLengthOfOptimalCompression(string s, int k) {const int n = s.length(); vector<int> vLen = { 0,1,2,10,100 };auto GetCodeLen = [&vLen](int len){int i = vLen.size() - 1;for (; (i >= 0) && (len < vLen[i]); i--);return i;};vector<vector<int>> dp(n + 1, vector<int>(k + 1, 100));dp[0][0] = 0;for (int i = 0; i < n; i++){//处理删除s[i]for (int j1 = 1; j1 <= min(i+1,k); j1++){dp[i+1][j1] = dp[i][j1-1];}//处理不删除s[i]for (int same = 0, diff = 0, preLen = i;preLen>=0; preLen--){if (s[preLen] == s[i]){same++;for (int j1 = diff; j1 <= min(i + 1, k); j1++){dp[i + 1][j1] = min(dp[i + 1][j1], dp[i + 1 - same - diff][j1 - diff] + GetCodeLen(same));} }else{diff++;}}} return *std::min_element(dp.back().begin() , dp.back().end());}
};
2023年2月 第一版
class Solution {
public:
int getLengthOfOptimalCompression(const string s, const int k) {
int pre[100 + 1][27][101];
memset(pre, 101, sizeof(pre));
pre[0][26][1] = 0;
for (const auto& ch : s)
{
int dp[100 + 1][27][101];
memset(dp, 101, sizeof(dp));
for (int iK = 0; iK <= k; iK++)
{
for (int j = 0; j < 27; j++)
{
for (int iNew = 0; iNew < 101; iNew++)
{
const int& iLen = pre[iK][j][iNew];
if (iLen > 100)
{
continue;
}
if (iK < k)
{//删除
dp[iK + 1][j][iNew] = min(dp[iK + 1][j][iNew], iLen);
}
if (j + ‘a’ != ch)
{
dp[iK][ch - ‘a’][1] = min(dp[iK][ch - ‘a’][1], iLen + 1);
}
else
{
const int iNewNum = min(100, iNew + 1);
dp[iK][ch - ‘a’][iNewNum] = min(dp[iK][ch - ‘a’][iNewNum], iLen + ((1 == iNew) || (9 == iNew) || (99 == iNew)));
}
}
}
}
memcpy(pre,dp, sizeof(pre));
}
int iMin = INT_MAX;
if (100 == s.length())
{
const char chMin = *std::min_element(s.begin(), s.end());
const char chMax = *std::max_element(s.begin(), s.end());
if (chMin == chMax)
{
iMin = 4;
}
}
for (int iK = 0; iK <= k; iK++)
{
for (int j = 0; j < 27; j++)
{
for (int iNew = 0; iNew < 101; iNew++)
{
if (pre[iK][j][iNew] < iMin)
{
iMin = pre[iK][j][iNew];
}
}
}
}
return iMin;
}
};
2023年2月 第二版
class Solution {
public:
int getLengthOfOptimalCompression(const string s, const int k) {
if (100 == s.length())
{
const char chMin = *std::min_element(s.begin(), s.end());
const char chMax = *std::max_element(s.begin(), s.end());
if (chMin == chMax)
{
const int iRemain = s.length() - k;
if (iRemain >= 100)
{
return 4;
}
if (iRemain >= 10)
{
return 3;
}
if (iRemain >= 2 )
{
return 2;
}
return iRemain;
}
}
int pre[100 + 1][27][11];
memset(pre, 101, sizeof(pre));
pre[0][26][1] = 0;
for (const auto& ch : s)
{
int dp[100 + 1][27][11];
memset(dp, 101, sizeof(dp));
for (int iK = 0; iK <= k; iK++)
{
for (int j = 0; j < 27; j++)
{
for (int iNew = 0; iNew < 11; iNew++)
{
const int& iLen = pre[iK][j][iNew];
if (iLen > 100)
{
continue;
}
if (iK < k)
{//删除
dp[iK + 1][j][iNew] = min(dp[iK + 1][j][iNew], iLen);
}
if (j + ‘a’ != ch)
{
dp[iK][ch - ‘a’][1] = min(dp[iK][ch - ‘a’][1], iLen + 1);
}
else
{
const int iNewNum = min(10, iNew + 1);
dp[iK][ch - ‘a’][iNewNum] = min(dp[iK][ch - ‘a’][iNewNum], iLen + ((1 == iNew) || (9 == iNew) || (99 == iNew)));
}
}
}
}
memcpy(pre, dp, sizeof(pre));
}
int iMin = INT_MAX;
for (int iK = 0; iK <= k; iK++)
{
for (int j = 0; j < 27; j++)
{
for (int iNew = 0; iNew < 11; iNew++)
{
if (pre[iK][j][iNew] < iMin)
{
iMin = pre[iK][j][iNew];
}
}
}
}
return iMin;
}
};
2023年2月版
class Solution {
public:
int getLengthOfOptimalCompression(const string s, const int k) {
if (100 == s.length())
{
const char chMin = *std::min_element(s.begin(), s.end());
const char chMax = *std::max_element(s.begin(), s.end());
if (chMin == chMax)
{
const int iRemain = s.length() - k;
if (iRemain >= 100)
{
return 4;
}
if (iRemain >= 10)
{
return 3;
}
if (iRemain >= 2 )
{
return 2;
}
return iRemain;
}
}
int pre[100 + 1][27][11];
memset(pre, 101, sizeof(pre));
pre[0][26][1] = 0;
for (const auto& ch : s)
{
int dp[100 + 1][27][11];
memset(dp, 101, sizeof(dp));
for (int iK = 0; iK <= k; iK++)
{
for (int j = 0; j < 27; j++)
{
for (int iNew = 1; iNew < 11; iNew++)
{
const int& iLen = pre[iK][j][iNew];
if (iLen > 100)
{
continue;
}
if (iK < k)
{//删除
dp[iK + 1][j][iNew] = min(dp[iK + 1][j][iNew], iLen);
}
if (j + ‘a’ != ch)
{
dp[iK][ch - ‘a’][1] = min(dp[iK][ch - ‘a’][1], iLen + 1);
}
else
{
const int iNewNum = min(10, iNew + 1);
dp[iK][ch - ‘a’][iNewNum] = min(dp[iK][ch - ‘a’][iNewNum], iLen + ((1 == iNew) || (9 == iNew) || (99 == iNew)));
}
}
}
}
memcpy(pre, dp, sizeof(pre));
}
int iMin = INT_MAX;
for (int iK = 0; iK <= k; iK++)
{
for (int j = 0; j < 27; j++)
{
for (int iNew = 1; iNew < 11; iNew++)
{
if (pre[iK][j][iNew] < iMin)
{
iMin = pre[iK][j][iNew];
}
}
}
}
return iMin;
}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【字符串】【行程码】1531. 压缩字符串
作者推荐 视频算法专题 本文涉及知识点 动态规划汇总 LeetCode 1531. 压缩字符串 II 行程长度编码 是一种常用的字符串压缩方法,它将连续的相同字符(重复 2 次或更多次)替换为字符和表示字符计数的数字(行程长度)…...

检测头篇 | 原创自研 | YOLOv8 更换 SEResNeXtBottleneck 头 | 附详细结构图
左图:ResNet 的一个模块。右图:复杂度大致相同的 ResNeXt 模块,基数(cardinality)为32。图中的一层表示为(输入通道数,滤波器大小,输出通道数)。 1. 思路 ResNeXt是微软研究院在2017年发表的成果。它的设计灵感来自于经典的ResNet模型,但ResNeXt有个特别之处:它采用…...
PHP语法
#本来是在学命令执行,所以学了学,后来发现,PHP语法和命令执行的关系好像没有那么大,不如直接学php的一些命令执行函数了。# #但是还是更一下,毕竟还是很多地方都要求掌握php作为脚本语言,所以就学了前面的…...
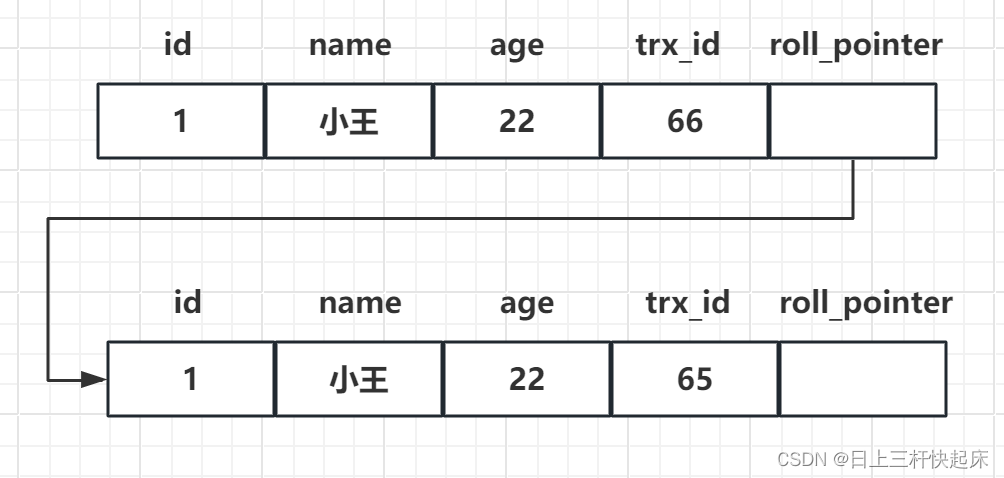
MySQL:三大日志(binlog、redolog、undolog)
再了解三个日志前我们先了解一下MySQL的两层架构: Server 层负责建立连接、分析和执行 SQL。MySQL 大多数的核心功能模块都在这实现,主要包括连接器,查询缓存、解析器、预处理器、优化器、执行器等。另外,所有的内置函数和所有跨…...

【QT+QGIS跨平台编译】之十二:【libpng+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文件目录 一、libpng介绍二、文件下载三、文件分析四、pro文件五、编译实践一、libpng介绍 PNG(Portable Network Graphics,便携式网络图形),是一种采用无损压缩算法的位图格式,支持索引、灰度、RGB三种颜色方案以及Alpha通道等特性。 PNG使用从LZ77派生的无损数据压缩算…...
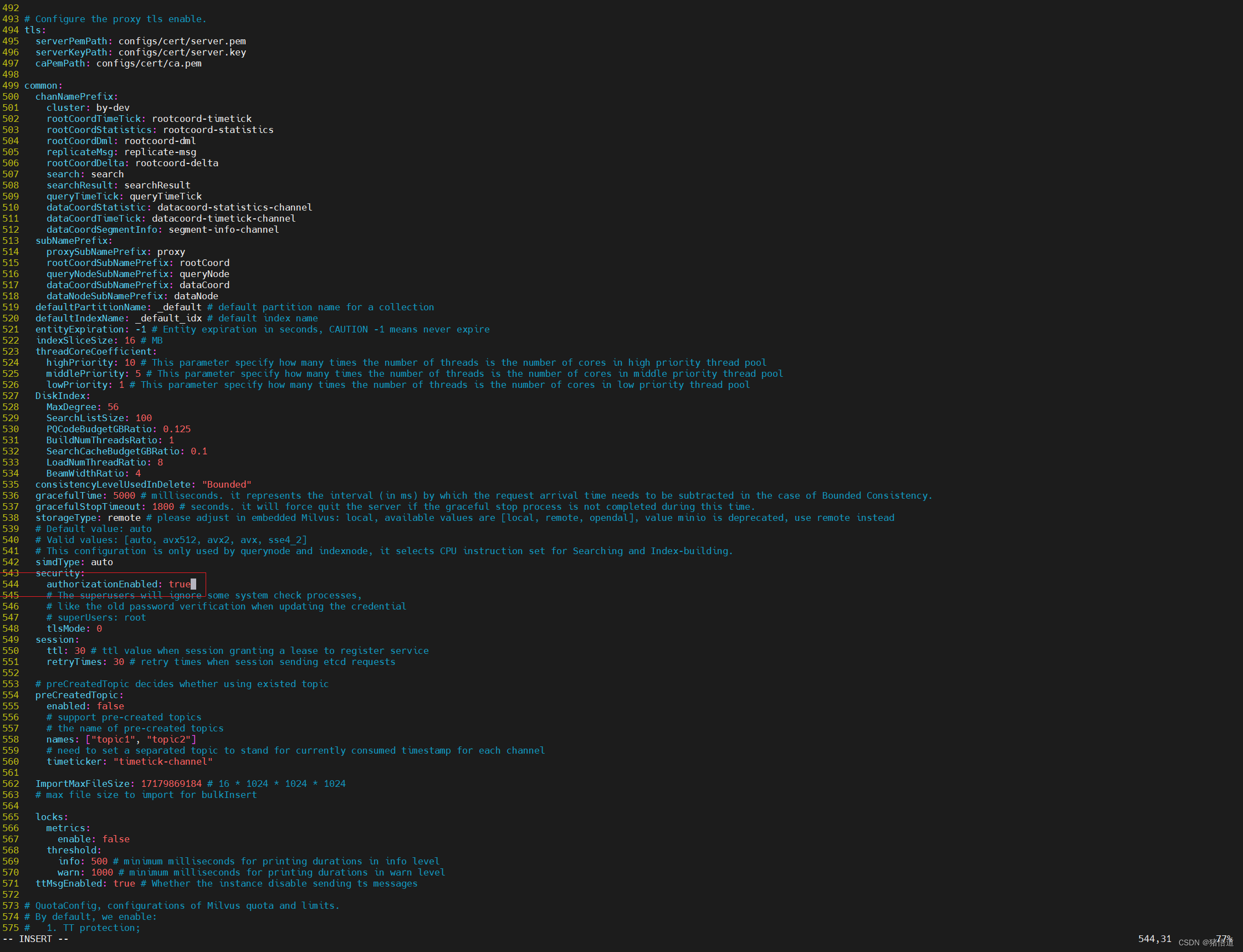
Windows 和 Anolis 通过 Docker 安装 Milvus 2.3.4
Windows 10 通过 Docker 安装 Milvus 2.3.4 一.Windows 安装 Docker二.Milvus 下载1.下载2.安装1.Windows 下安装(指定好Docker文件目录)2.Anolis下安装 三.数据库访问1.ATTU 客户端下载 一.Windows 安装 Docker Docker 下载 双击安装即可,安…...
)
JUC并发编程与源码分析学习笔记(三)
目录 五十六、JMM之入门简介 五十七、JMM之学术定义和作用 五十八、JMM之三大特性 五十九、JMM之多线程对变量的读写过程 六十、JMM之happens-before-上集 六十一、JMM之happens-before-下集 五十六、JMM之入门简介 Java内存模型之JMM 1、先从大厂面试题开始 ①、你知道…...
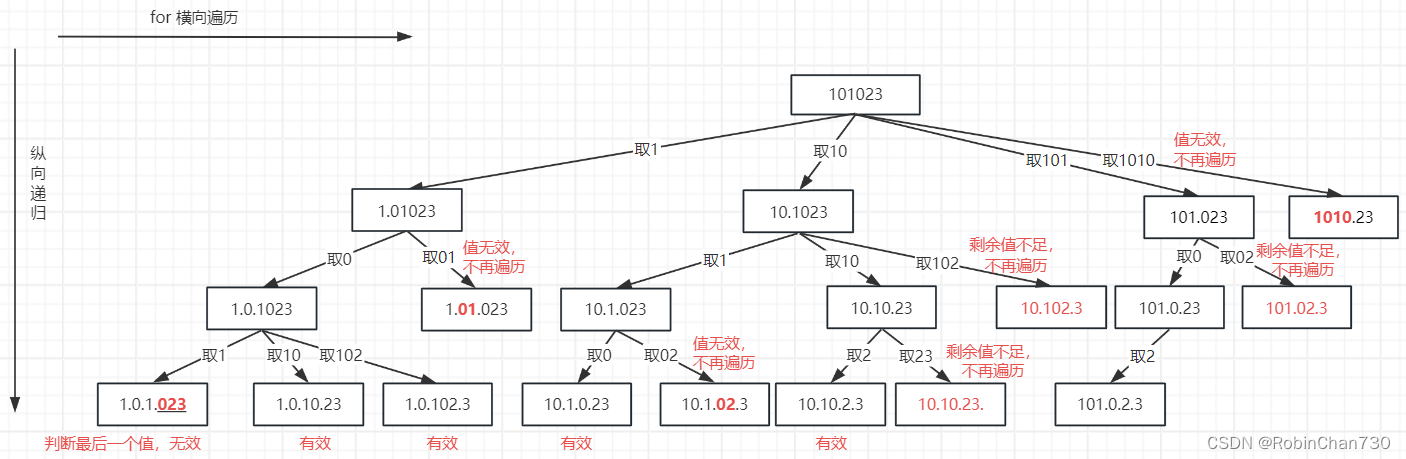
力扣日记1.28-【回溯算法篇】93. 复原 IP 地址
力扣日记:【回溯算法篇】93. 复原 IP 地址 日期:2023.1.28 参考:代码随想录、力扣 93. 复原 IP 地址 题目描述 难度:中等 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0&…...

Java 的反射学习总结
目录 一、什么是反射? 二、如何获取类对象? 三、如何通过类对象来创建类的对象? 四、类对象获取类构造器的方式 五、通过类对象获取类的属性 六、通过类对象获取类的方法 一、什么是反射? 反射是指在运行时动态地获取、检查…...

图论第二天|695. 岛屿的最大面积 1020. 飞地的数量 130. 被围绕的区域 417. 太平洋大西洋水流问题 827.最大人工岛
目录 Leetcode695. 岛屿的最大面积Leetcode1020. 飞地的数量Leetcode130. 被围绕的区域Leetcode417. 太平洋大西洋水流问题Leetcode827.最大人工岛 Leetcode695. 岛屿的最大面积 文章链接:代码随想录 题目链接:695. 岛屿的最大面积 思路:dfs …...
【JavaScript 基础入门】02 JavaScrip 详细介绍
JavaScrip 详细介绍 目录 JavaScrip 详细介绍1. JavaScript 是什么2. JavaScript的作用3. HTML/CSS/JS 的关系4. 浏览器执行 JS 简介5. JavaScript 的组成6. JavaScript 的特点 1. JavaScript 是什么 JavaScript,通常缩写为 JS,是一种高级的,…...
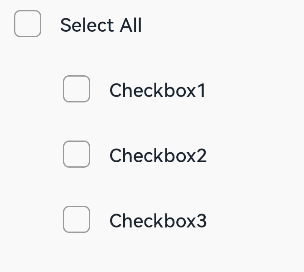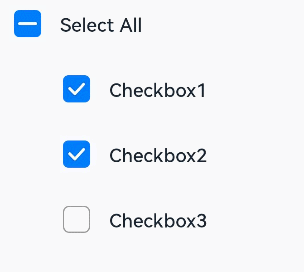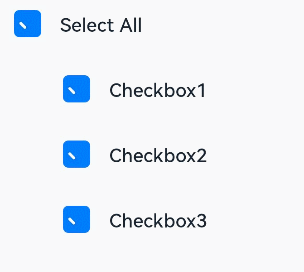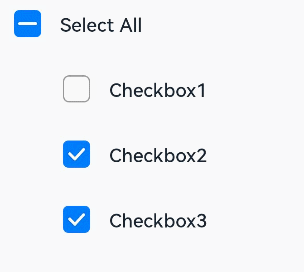
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之CheckboxGroup组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之CheckboxGroup组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、CheckboxGroup组件 提供多选框组件,通常用于某选项的打开或关…...

【极数系列】Flink配置参数如何获取?(06)
文章目录 gitee码云地址简介概述01 配置值来自.properties文件1.通过路径读取2.通过文件流读取3.通过IO流读取 02 配置值来自命令行03 配置来自系统属性04 注册以及使用全局变量05 Flink获取参数值Demo1.项目结构2.pom.xml文件如下3.配置文件4.项目主类5.运行查看相关日志 gite…...
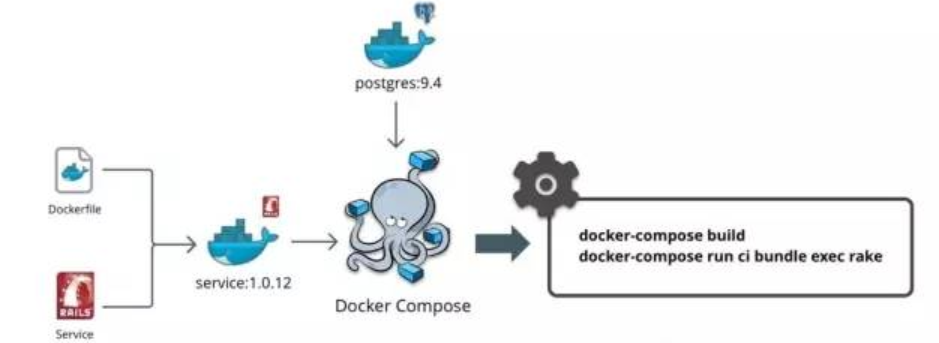
【docker】linux系统docker的安装及使用
一、docker应用的安装 1.1 安装方式 Docker的自动化安装,即使用提供的一键安装的脚本,进行安装。 官方的一键安装方式:curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun 国内 daocloud一键安装命令:curl -s…...
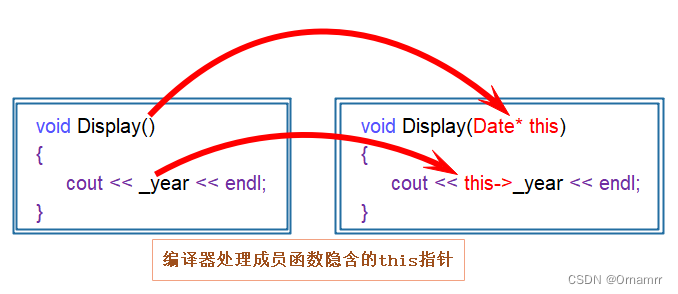
【C++】一题掌握空指针
今天看见一道面试题,比较有意思,这一分享出来: 1.下面程序能编译通过吗? 2.下面程序会崩溃吗?在哪里崩溃 class A {public:void PrintA(){cout<<_a<<endl;}void Show(){cout<<"Show()"&…...

初识HarmonyOS
一、HarmonyOS VS Android 相信很多关注鸿蒙的⼈,都会关注的⼀个焦点话题,那就是HarmonyOS是不是Android的套壳,对于这个话题,我只想阐明以下⼏个观点: HarmonyOS并不是Android的替代品,HarmonyOS与Android并⾮同⼀个赛道。HarmonyOS⽬前缺乏⽣态⽀持这⼀点远远⽐不上An…...
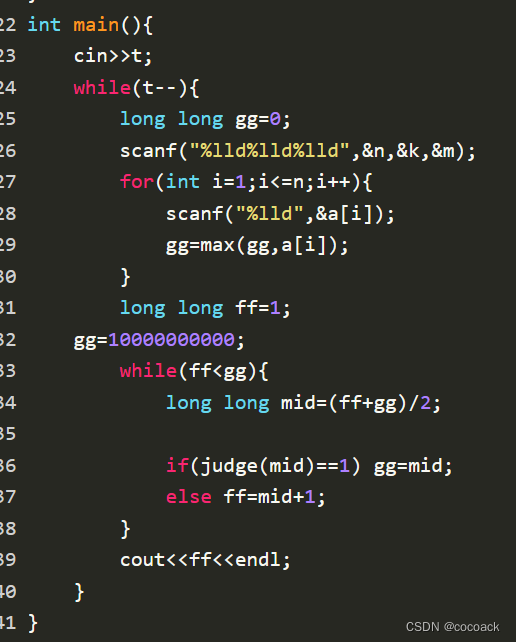
备战蓝桥杯---二分(入门)
话不多说,先来个模板题来回顾一下上次讲的: 下面是AC代码: 下面进入正题: 本题对1,2行与3,4行组合,再用二分查找即可实现n^2logn的复杂度。 下面是AC代码: 接题: 让我们…...

开发 Chrome 浏览器插件时进行 Vue3+Vite 多页面多入口配置
使用 Vite 开发 Chrome 插件时,构建多页面以及多 js 文件 因为发现 Vite 多页面构建有很多分歧以及问题点,所以我把我在 Chrome 插件开发上面使用到的 Vite 多页面以及多入口文件构建配置单独拿出来 开发 Chrome 插件是,一般会需要一个 popup…...

MacOS X 中 OpenGL 环境搭建 Makefile的方式
1,预备环境 安装 brew: /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)" 安装glfw: brew install glfw 安装glew: brew install glew 2.编译 下载源代码…...
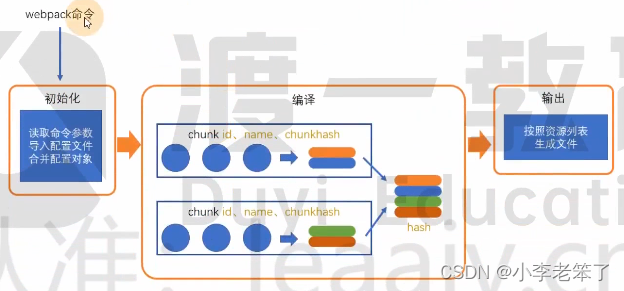
前端工程化之:webpack1-6(编译过程)
一、webpack编译过程 webpack 的作用是将源代码编译(构建、打包)成最终代码。 整个过程大致分为三个步骤: 初始化编译输出 1.初始化 初始化时我们运行的命令 webpack 为核心包, webpack-cli 提供了 webpack 命令,通过…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
