备战蓝桥杯---二分(入门)
话不多说,先来个模板题来回顾一下上次讲的:
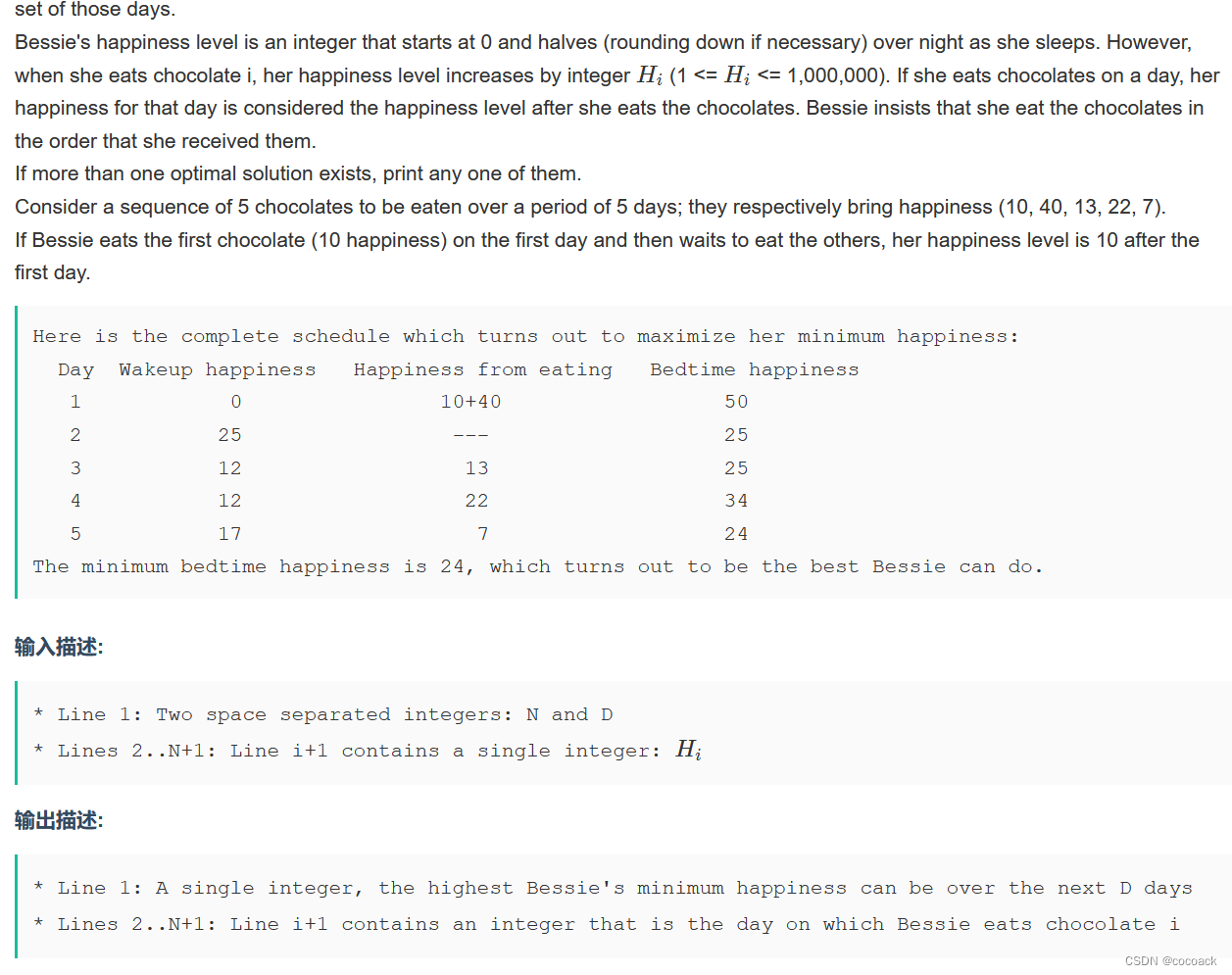
下面是AC代码:
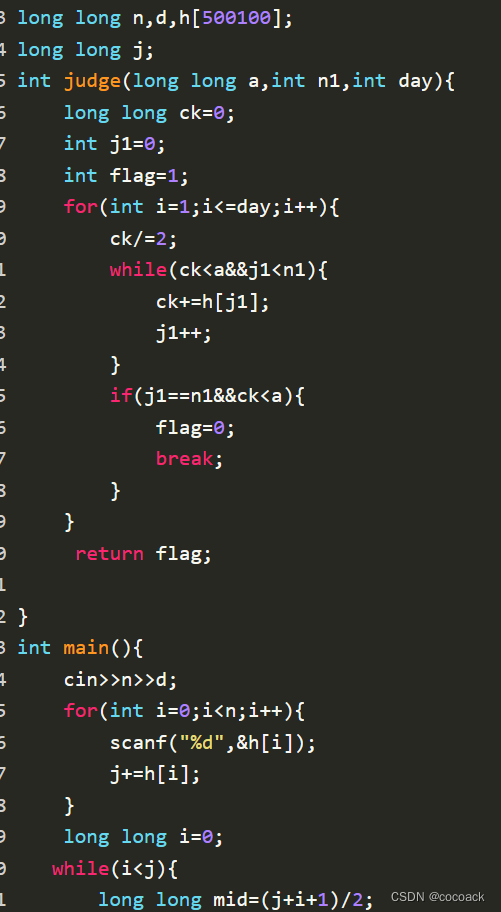

下面进入正题:

本题对1,2行与3,4行组合,再用二分查找即可实现n^2logn的复杂度。
下面是AC代码:
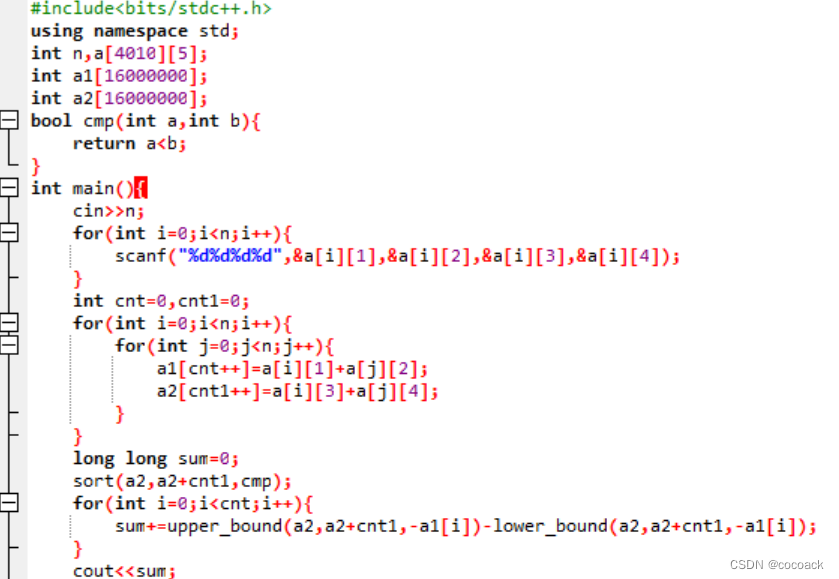
接题:
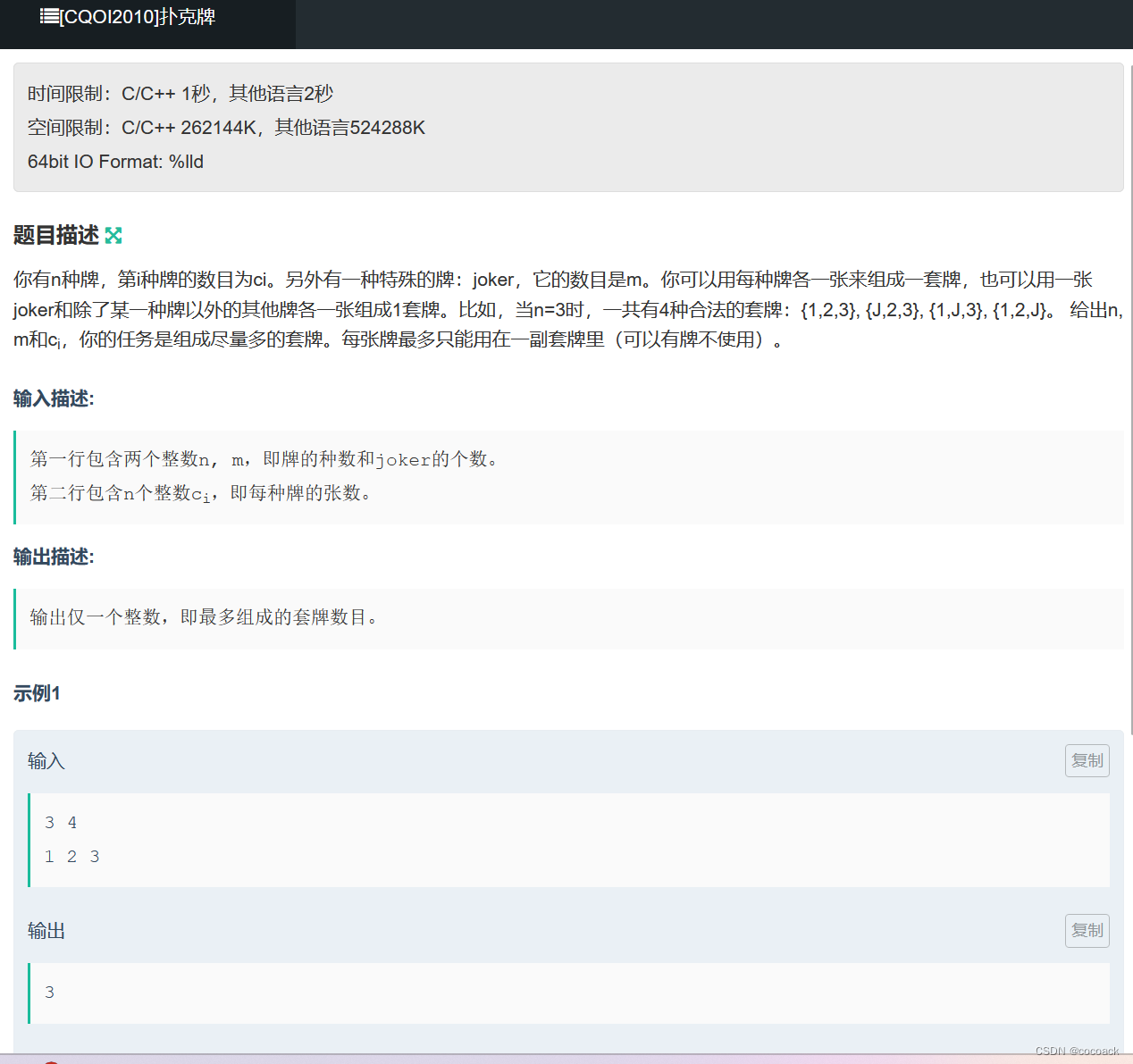
让我们分析一下:
首先这是一个单调函数,因此可以用而二分+检验,那我们如何检验呢?
我们要验证x套是否可行,假设没有joker的存在,那么每种牌都要x个,于是我们统计每种共缺多少,如果它大于joker则不行,所需joker多于套数也不行。
下面是AC代码:

让我们来道难一点的题:
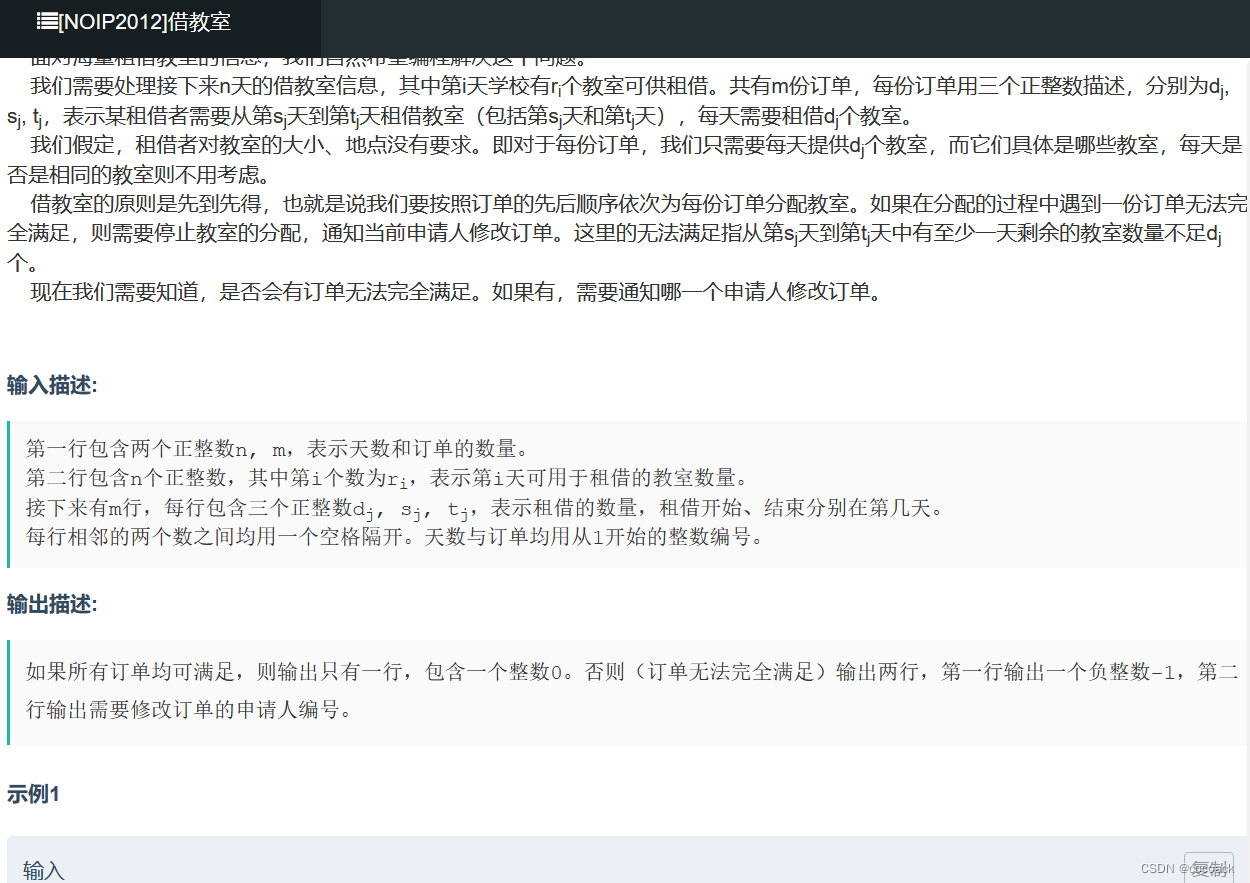
本题很容易想到用线段树去维护,那我们不妨想想可以用二分写吗?
我们分析一下:假设ans为答案,那么它后面肯定不符合。那如何验证x是否符合呢?只要看到其过程中是否有不符合的情况即可,很容易想到用差分去维护。
当然,有人会问为什么不在求差分的时候直接暴力求第一个不符合的地方而要用二分来做。则每次还要进行一场判断,复杂度为n^2,而用二分nlogn
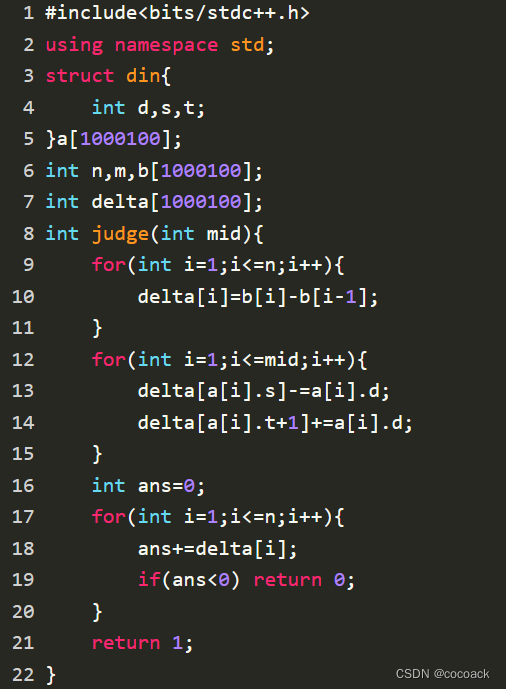
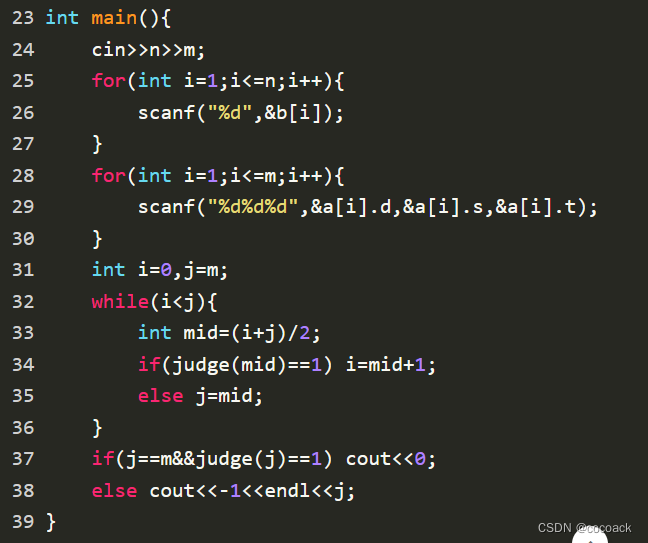
下面为AC代码:
让我们以这一题来结束吧:
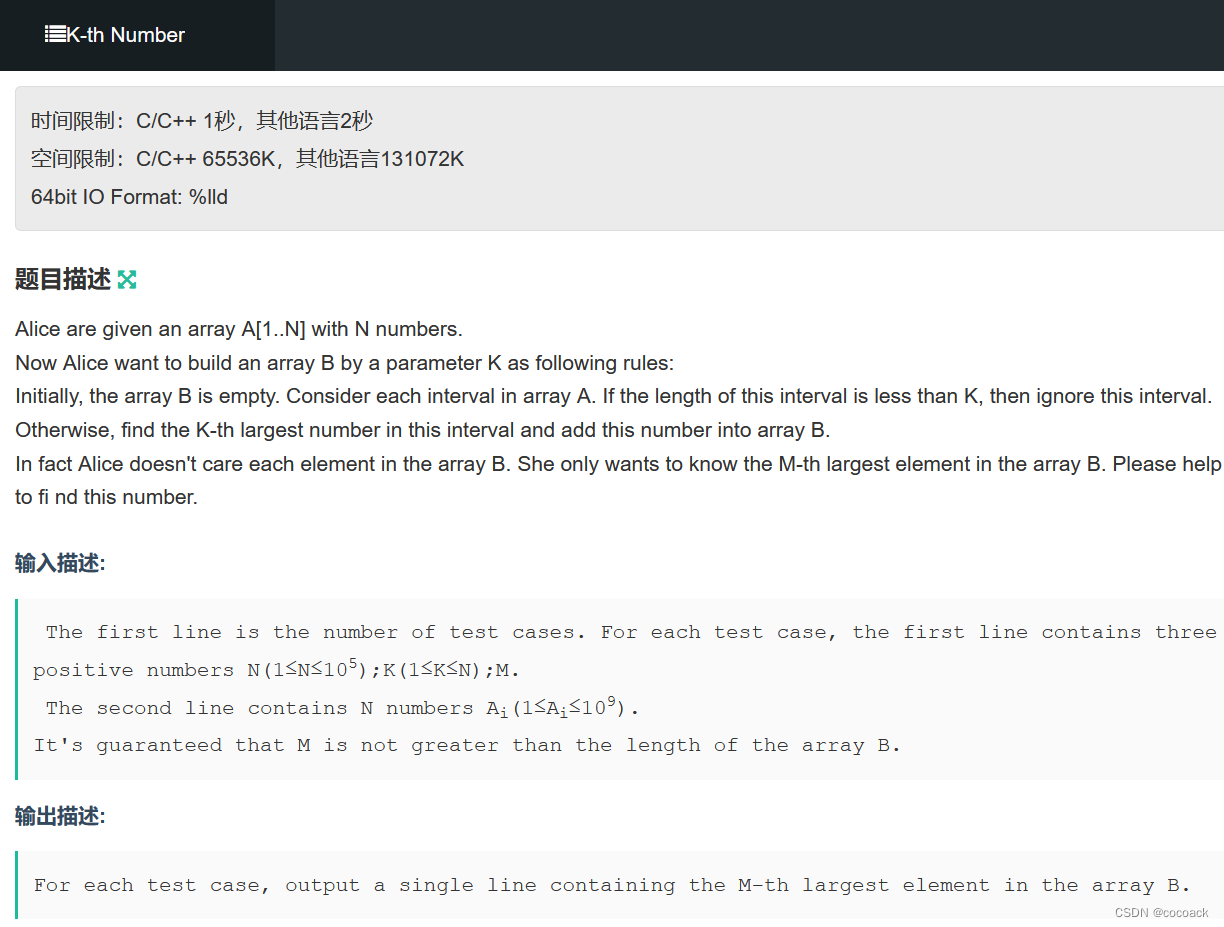
下面是分析:

下面是AC代码(一定要开long long):
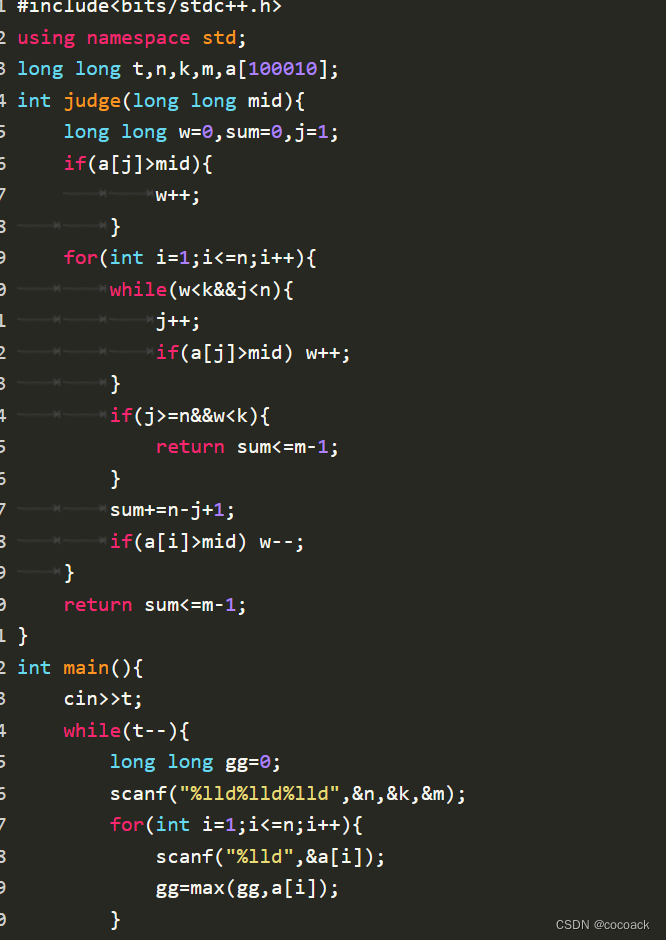
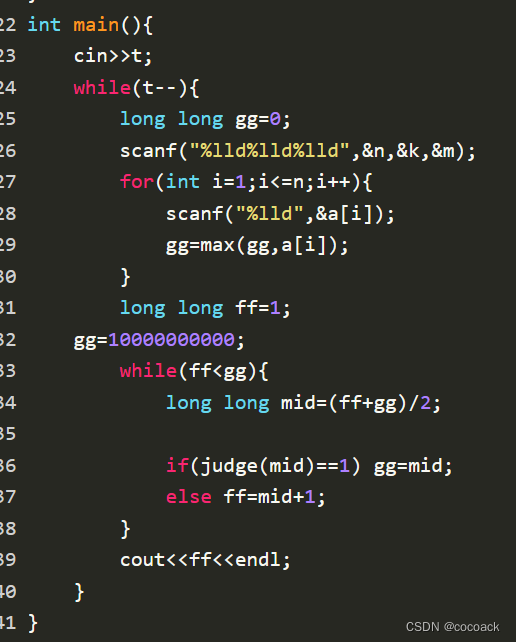
相关文章:

备战蓝桥杯---二分(入门)
话不多说,先来个模板题来回顾一下上次讲的: 下面是AC代码: 下面进入正题: 本题对1,2行与3,4行组合,再用二分查找即可实现n^2logn的复杂度。 下面是AC代码: 接题: 让我们…...

开发 Chrome 浏览器插件时进行 Vue3+Vite 多页面多入口配置
使用 Vite 开发 Chrome 插件时,构建多页面以及多 js 文件 因为发现 Vite 多页面构建有很多分歧以及问题点,所以我把我在 Chrome 插件开发上面使用到的 Vite 多页面以及多入口文件构建配置单独拿出来 开发 Chrome 插件是,一般会需要一个 popup…...

MacOS X 中 OpenGL 环境搭建 Makefile的方式
1,预备环境 安装 brew: /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)" 安装glfw: brew install glfw 安装glew: brew install glew 2.编译 下载源代码…...
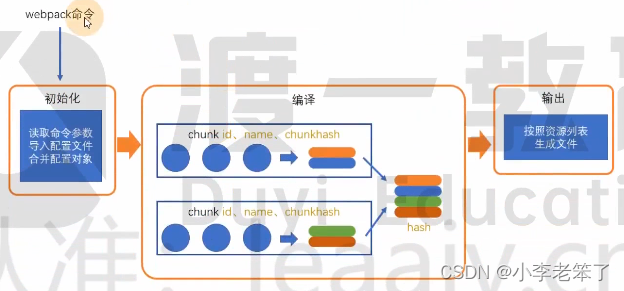
前端工程化之:webpack1-6(编译过程)
一、webpack编译过程 webpack 的作用是将源代码编译(构建、打包)成最终代码。 整个过程大致分为三个步骤: 初始化编译输出 1.初始化 初始化时我们运行的命令 webpack 为核心包, webpack-cli 提供了 webpack 命令,通过…...

javaweb学习问题集
1 创建一个Javaweb项目 因为项目要放在tomcat10里运行,在添加tomcat10的依赖时,右键模块没有add frameworks support ,解决方法:按两下shift键,直接搜索 add frameworks support index.jsp文件我们已经不用了 我们在ideal上开发…...
java—AWT
AWT 课程:1、GUI编程简介_哔哩哔哩_bilibili 一.介绍 包含了很多类和接口!GUI!元素:窗口、按钮、文本框java.awt 二.窗口 1.构造 2.方法 // 实例化frame类Frame frame new Frame("这个一个框");// 设置可见性frame.…...
SQL注入-sqli-labs-master第一关
实验环境: Nginx.1.15.11 MySQL:5.7.26 实验步骤: 1.第一步: 在id1后加入一个闭合符号,如果报错,再在后面加上 -- 将后面注释掉,如果不报错,则证明为字符型。 http://127.0.0.1/…...
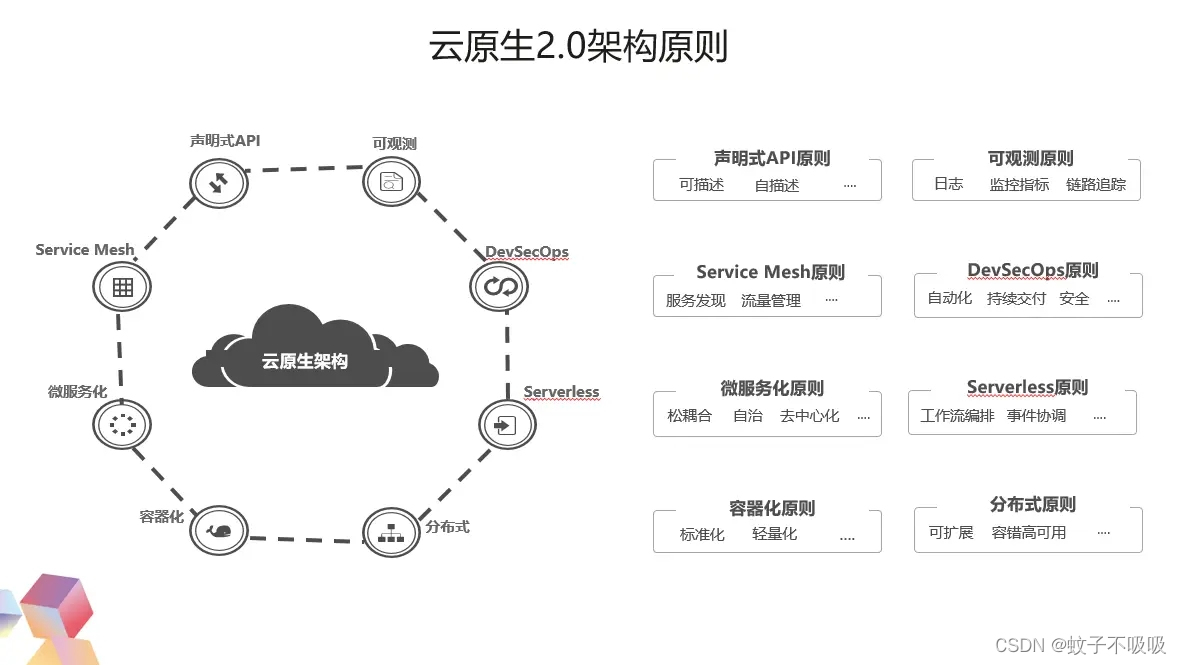
简述云原生基础定义及关键技术
云原生是什么 云原生是面向“云”而设计的应用,因此技术部分依赖于传统云计算的 3 层概念,基础设施即服务(IaaS)、平台即服务(PaaS)和软件即服务(SaaS)。 例如,敏捷的不可变基础设施交付类似于 IaaS,用来提供计算网络存储等基础资源,这些资源是可编程且不可变的,直…...

游戏中排行榜的后台实现
游戏中经常会有排行榜需求需要实现,例如常见的战力排行榜、积分排行榜等等。 排行榜一般会用到 Redis 来实现,原因是: Redis 基于内存操作,速度快Redis 提供了高效的有序集合 zset 例如创建一个名为 rank 的排行榜 # 为用户use…...

《动手学深度学习(PyTorch版)》笔记3.1
Chapter3 Linear Neural Networks 3.1 Linear Regression 3.1.1 Basic Concepts 我们通常使用 n n n来表示数据集中的样本数。对索引为 i i i的样本,其输入表示为 x ( i ) [ x 1 ( i ) , x 2 ( i ) , . . . , x n ( i ) ] ⊤ \mathbf{x}^{(i)} [x_1^{(i)}, x_2…...
【贪吃蛇:C语言实现】
文章目录 前言1.了解Win32API相关知识1.1什么是Win32API1.2设置控制台的大小、名称1.3控制台上的光标1.4 GetStdHandle(获得控制台信息)1.5 SetConsoleCursorPosition(设置光标位置)1.6 GetConsoleCursorInfo(获得光标…...
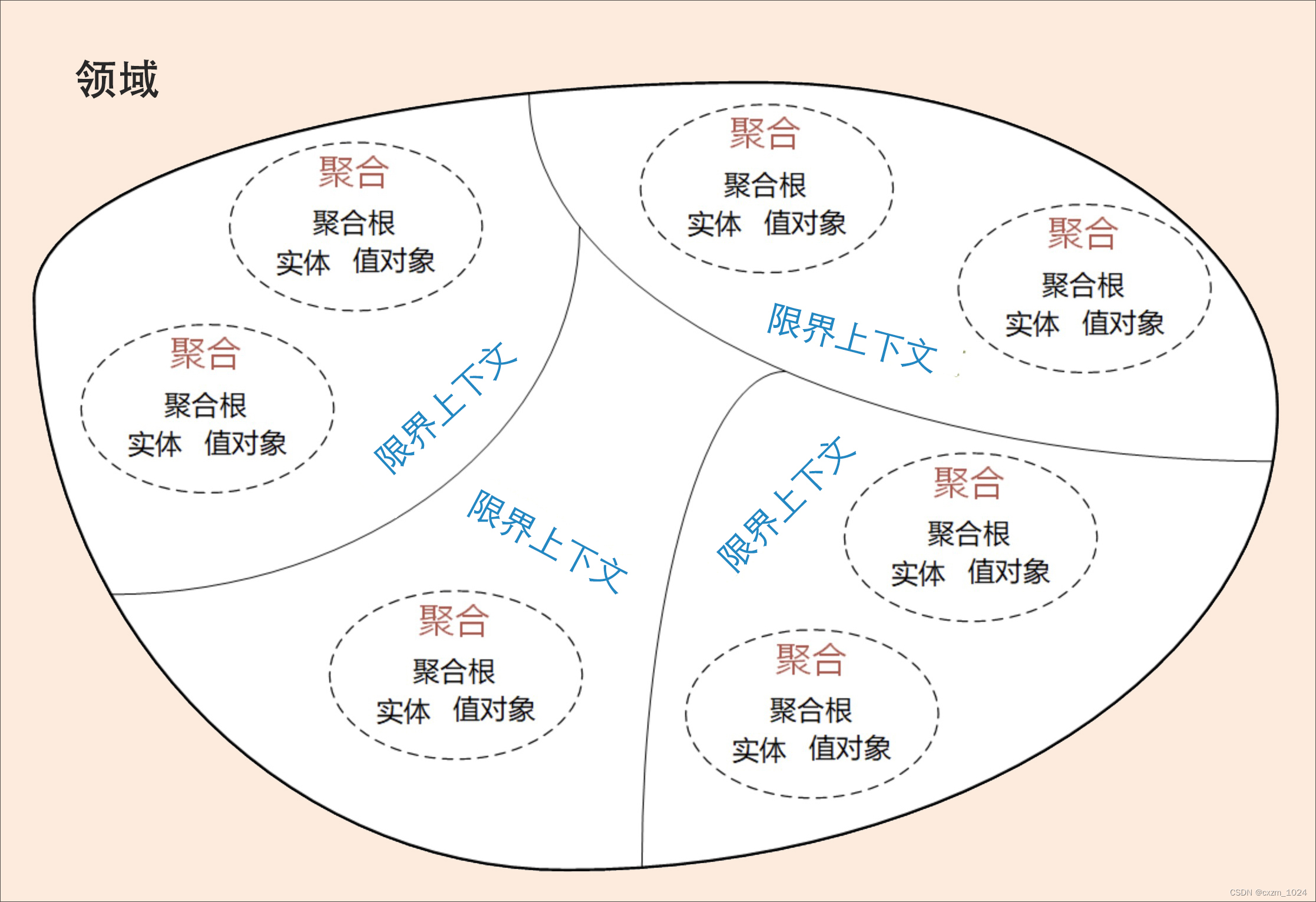
01.领域驱动设计:微服务设计为什么要选择DDD学习总结
目录 1、前言 2、软件架构模式的演进 3、微服务设计和拆分的困境 4、为什么 DDD适合微服务 5、DDD与微服务的关系 6、总结 1、前言 我们知道,微服务设计过程中往往会面临边界如何划定的问题,不同的人会根据自己对微服务的理 解而拆分出不同的微服…...
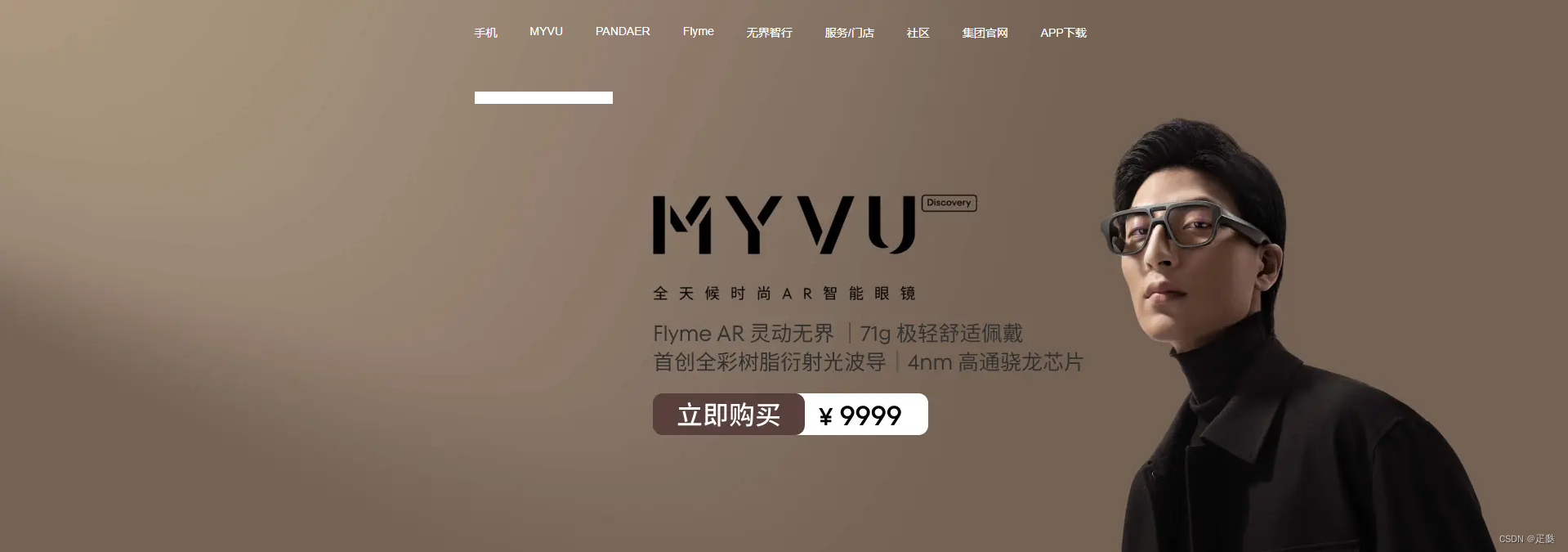
写静态页面——魅族导航_前端页面练习
0、效果: 1、html代码:: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><…...

Go 命令行解析 flag 包之快速上手
本篇文章是 Go 标准库 flag 包的快速上手篇。 概述 开发一个命令行工具,视复杂程度,一般要选择一个合适的命令行解析库,简单的需求用 Go 标准库 flag 就够了,flag 的使用非常简单。 当然,除了标准库 flag 外&#x…...
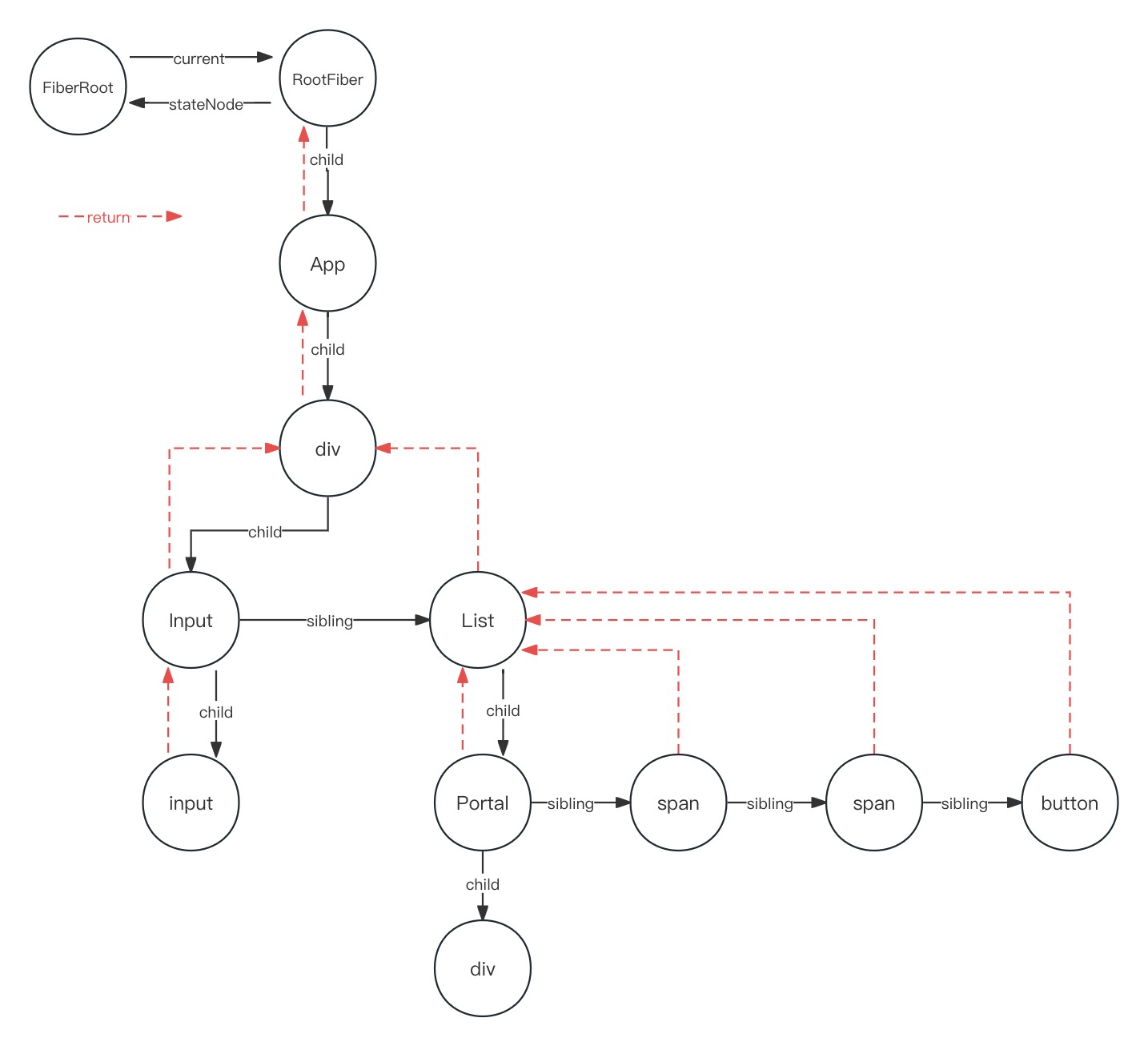
React16源码: React中commitAllHostEffects内部的commitDeletion的源码实现
commitDeletion 1 )概述 在 react commit 阶段的 commitRoot 第二个while循环中调用了 commitAllHostEffects,这个函数不仅仅处理了新增节点,更新节点最后一个操作,就是删除节点,就需要调用 commitDeletion࿰…...
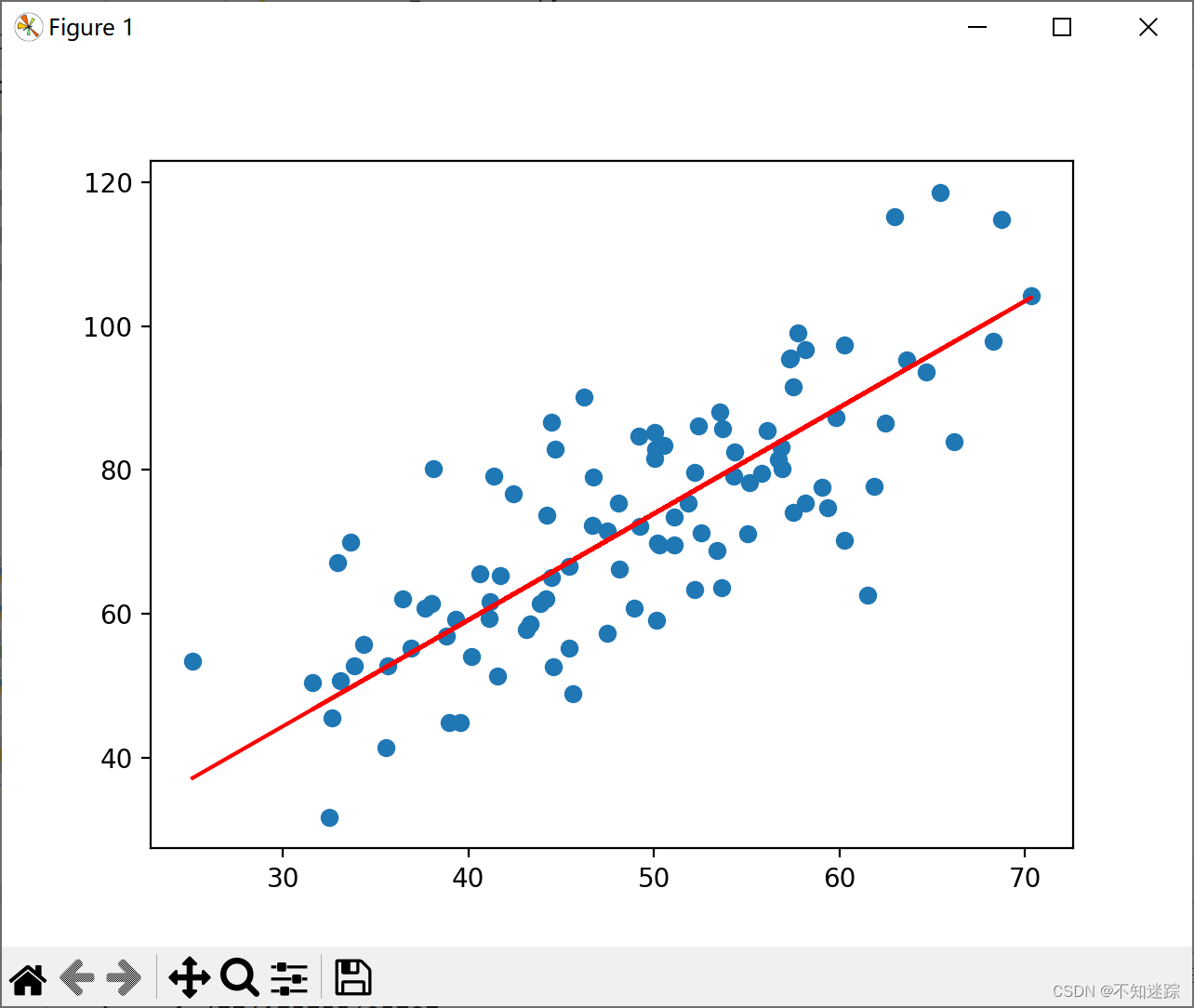
[机器学习]简单线性回归——梯度下降法
一.梯度下降法概念 2.代码实现 # 0. 引入依赖 import numpy as np import matplotlib.pyplot as plt# 1. 导入数据(data.csv) points np.genfromtxt(data.csv, delimiter,) points[0,0]# 提取points中的两列数据,分别作为x,y …...
2024年搭建幻兽帕鲁服务器价格多少?如何自建Palworld?
自建幻兽帕鲁服务器租用价格表,2024阿里云推出专属幻兽帕鲁Palworld游戏优惠服务器,配置分为4核16G和4核32G服务器,4核16G配置32.25元/1个月、3M带宽96.75元/1个月、8核32G配置10M带宽90.60元/1个月,8核32G配置3个月271.80元。ECS…...
『OpenCV-Python|鼠标作画笔』
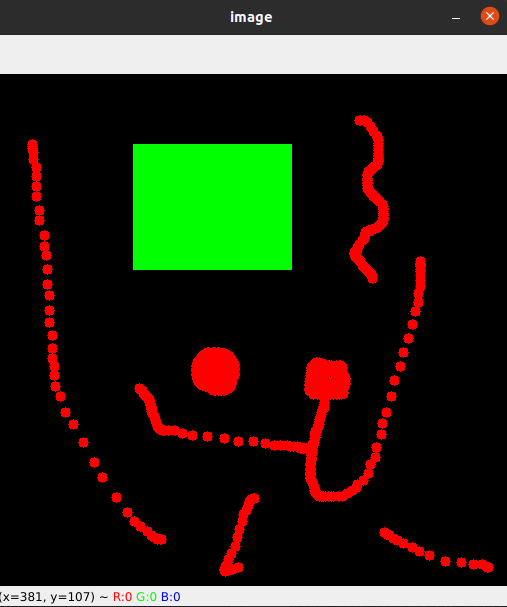
Opencv-Python教程链接:https://opencv-python-tutorials.readthedocs.io/ 本文主要介绍OpenCV-Python如何将鼠标作画笔绘制圆或者矩形。 示例一:图片上双击的位置绘制一个圆圈 首先创建一个鼠标事件回调函数,鼠标事件发生时就会被执行。鼠标…...

关于如何利用ChatGPT提高编程效率的
自从去年ChatGPT3.5推出以后,这一年时间在编程过程中我也在慢慢熟悉人工智能的使用,目前来看即使是免费的ChatGPT3.5对于编程效率的提升也是有很大帮助的,虽然在使用过程中确实出现了一些问题,本文记录下我的一些心得体会和用法。…...

Excel VBA ——从MySQL数据库中导出一个报表-笔记
本文主要涉及: VBA中数据库连接参数改成从配置文件获取 VBA连接MySQL数据库 VBA读MySQL数据库 演示两种写入工作簿的代码实现系统环境: Windows 10 64bit Excel 365 64bit WAMP(3.2.2.2 64bit)集成的MariaDB版本为10.4.10&#…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
