LC 2846. 边权重均等查询
2846. 边权重均等查询
难度: 困难
题目大意:
现有一棵由
n个节点组成的无向树,节点按从0到n - 1编号。给你一个整数n和一个长度为n - 1的二维整数数组edges,其中edges[i] = [ui, vi, wi]表示树中存在一条位于节点ui和节点vi之间、权重为wi的边。另给你一个长度为
m的二维整数数组queries,其中queries[i] = [ai, bi]。对于每条查询,请你找出使从ai到bi路径上每条边的权重相等所需的 最小操作次数 。在一次操作中,你可以选择树上的任意一条边,并将其权重更改为任意值。注意:
- 查询之间 相互独立 的,这意味着每条新的查询时,树都会回到 初始状态 。
- 从
ai到bi的路径是一个由 不同 节点组成的序列,从节点ai开始,到节点bi结束,且序列中相邻的两个节点在树中共享一条边。返回一个长度为
m的数组answer,其中answer[i]是第i条查询的答案。提示:
1 <= n <= 10^4edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= wi <= 26- 生成的输入满足
edges表示一棵有效的树1 <= queries.length == m <= 2 * 10^4queries[i].length == 20 <= ai, bi < n
示例 1:
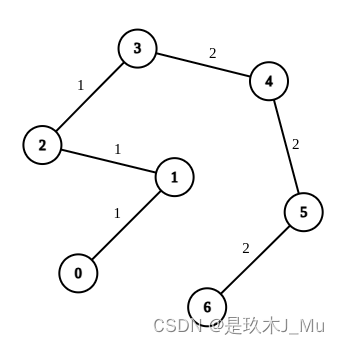
输入:n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出:[0,0,1,3]
解释:第 1 条查询,从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此,答案为 0 。
第 2 条查询,从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 0 。
第 3 条查询,将边 [2,3] 的权重变更为 2 。在这次操作之后,从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 1 。
第 4 条查询,将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后,从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
分析
如果暴力写的话, 那么对于每一个查询,我们要dfs一遍,每一遍存一下路径上的边权得数量,最后用总的数量减去最多的变得数量就是答案,这是一个小贪心的思路,那么考虑一下数据范围,如果暴力写的话,时间复杂度是 O ( n 2 ) O(n^2) O(n2),肯定会超时的,但是也吧暴力写法的代码贴出来。
723 / 733 个通过的测试用例
暴力 dfs (会超时)
class Solution {
public:vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {int m = queries.size();vector<int> e(n << 1), ne(n << 1), h(n, -1), w(n << 1), ans(m); // 链式向前星int cnt[27], idx = 0;// addfunction<void(int, int, int)> add = [&](int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;e[idx] = a, ne[idx] = h[b], w[idx] = c, h[b] = idx ++;}; // add// dfsfunction<bool(int, int, int)> dfs = [&](int u, int b, int fa) {if (u == b) {return true;}for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (j == fa) continue;if (dfs(j, b, u)) {++ cnt[w[i]];return true;}}return false;}; // dfsfor (int i = 0; i < n - 1; i ++ ) {int a = edges[i][0], b = edges[i][1], w = edges[i][2];add(a, b, w);}for (int i = 0; i < m; i ++) {memset(cnt, 0, sizeof cnt); // 每次清空数组int a = queries[i][0], b = queries[i][1];dfs(a, b, -1);int res = 0, sum = 0;for (int i = 1; i <= 26; i ++) {sum += cnt[i];res = max(res, cnt[i]);}ans[i] = sum - res;}return ans;}
};
时间复杂度: O ( n ∗ m ∗ W ) O(n*m*W) O(n∗m∗W) (本题 W = 26)
分析
我们可以用最近公共祖先的思想,选定一个根节点,假设是0,那么定义一个cnt[i][w]表示节点i到根节点的路径中边权为w(1 <= w <= 26)的边的数量,那么i到j之间边权为w的边数是 t a = c n t [ i ] [ w ] + c n t [ j ] [ w ] − 2 ∗ c n t [ l c a ( i , j ) ] [ w ] t_a = cnt[i][w] + cnt[j][w] - 2 * cnt[lca(i, j)][w] ta=cnt[i][w]+cnt[j][w]−2∗cnt[lca(i,j)][w],lca(i, j)表示节点i和节点j的最近公共祖先, 那么要替换的边数就是
∑ i = 1 26 t i − max 1 < = i < = 26 t i \sum_{i = 1}^{26} {t_i} - \max_{1 <= i <= 26}t_i i=1∑26ti−1<=i<=26maxti
使用离线算法tarjan算法模板
tarjan + 并查集
class Solution {
public:using PII = pair<int, int>;vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {int m = queries.size();vector<unordered_map<int, int>> g(n);for (auto& e : edges) {g[e[0]][e[1]] = e[2];g[e[1]][e[0]] = e[2];}vector<vector<PII>> q(n); for (int i = 0; i < m; i ++ ){q[queries[i][0]].push_back({queries[i][1], i});q[queries[i][1]].push_back({queries[i][0], i});}vector<int> lca(m), vis(n), p(n);iota(p.begin(), p.end(), 0);vector<vector<int>> cnt(n, vector<int>(27));function<int(int)> find = [&](int x) {if (x != p[x]) p[x] = find(p[x]);return p[x];};function<void(int, int)> tarjan = [&](int u, int fa) {if (fa != -1) {cnt[u] = cnt[fa];++ cnt[u][g[u][fa]];}p[u] = u;for (auto& e : g[u]) {if (e.first == fa) continue;tarjan(e.first, u);p[e.first] = u;}for (auto& e : q[u]) {if (u != e.first && !vis[e.first]) continue;lca[e.second] = find(e.first);}vis[u] = 1;};tarjan(0, -1);vector<int> res(m);for (int i = 0; i < m; i ++ ){int sum = 0, mx = 0;for (int j = 1; j <= 26;j ++) {int t = cnt[queries[i][0]][j] + cnt[queries[i][1]][j] - 2 * cnt[lca[i]][j];mx = max(mx, t);sum += t;}res[i] = sum - mx;}return res;}
};
时间复杂度: O ( ( m + n ) × W + m × l o g n ) O((m+n)×W+m×logn) O((m+n)×W+m×logn) (本题 W = 26)
在线lca算法
const int N = 10010;
class Solution {
public:int e[N << 1], ne[N << 1], w[N << 1], h[N], idx;int fa[N][15], depth[N];int cnt[N][27], cntn[27];int q[N];void bfs() {int hh = 0, tt = 0;q[0] = 1;memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[1] = 1;while (hh <= tt) {int t = q[hh ++ ];for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (depth[j] > depth[t] + 1) {depth[j] = depth[t] + 1;q[ ++ tt] = j;fa[j][0] = t;for (int k = 1; k <= 14; k ++ )fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}}// dfs版本void dfs_dep(int u, int father) {depth[u] = depth[father] + 1;fa[u][0] = father;for (int i = 1; i <= 14; i ++) fa[u][i] = fa[fa[u][i - 1]][i - 1];for (int i = h[u]; ~i; i = ne[i]) {if (e[i] != father) {dfs_dep(e[i], u);}}}void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;}void dfs(int u, int fa) {memcpy(cnt[u], cntn, sizeof cntn);for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (fa == j) continue;cntn[w[i]] ++;dfs(j, u);cntn[w[i]] -- ;}}int lca(int a, int b){if (depth[a] < depth[b]) swap(a, b);for (int k = 14; k >= 0; k -- )if (depth[fa[a][k]] >= depth[b]) a = fa[a][k];if (a == b) return a;for (int k = 14; k >= 0; k -- ) {if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];}}return fa[a][0];}vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {memset(h, -1,sizeof h);for (int i = 0; i < edges.size(); i ++ ) {int a = edges[i][0], b = edges[i][1], c = edges[i][2];a ++, b ++ ;add(a, b, c), add(b, a, c);}bfs();// dfs_dep(1, 0); // dfs_dep版本dfs(1, -1);vector<int> ans(queries.size());for (int i = 0; i < queries.size(); i ++ ) {int a = queries[i][0], b = queries[i][1];a ++, b ++ ;int p = lca(a, b);vector<int> s(27);for (int j = 1; j <= 26; j ++ )s[j] += cnt[a][j] + cnt[b][j] - cnt[p][j] * 2;int sum = 0, maxv = 0;for (int j = 1; j <= 26; j ++ ) {maxv = max(maxv, s[j]);sum += s[j];}ans[i] = sum - maxv;}return ans;}
};
时间复杂度: O ( m l o g n ) O(mlogn) O(mlogn)
相关文章:

LC 2846. 边权重均等查询
2846. 边权重均等查询 难度: 困难 题目大意: 现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] [ui, vi, wi] 表示树中存在一条位于节点 …...
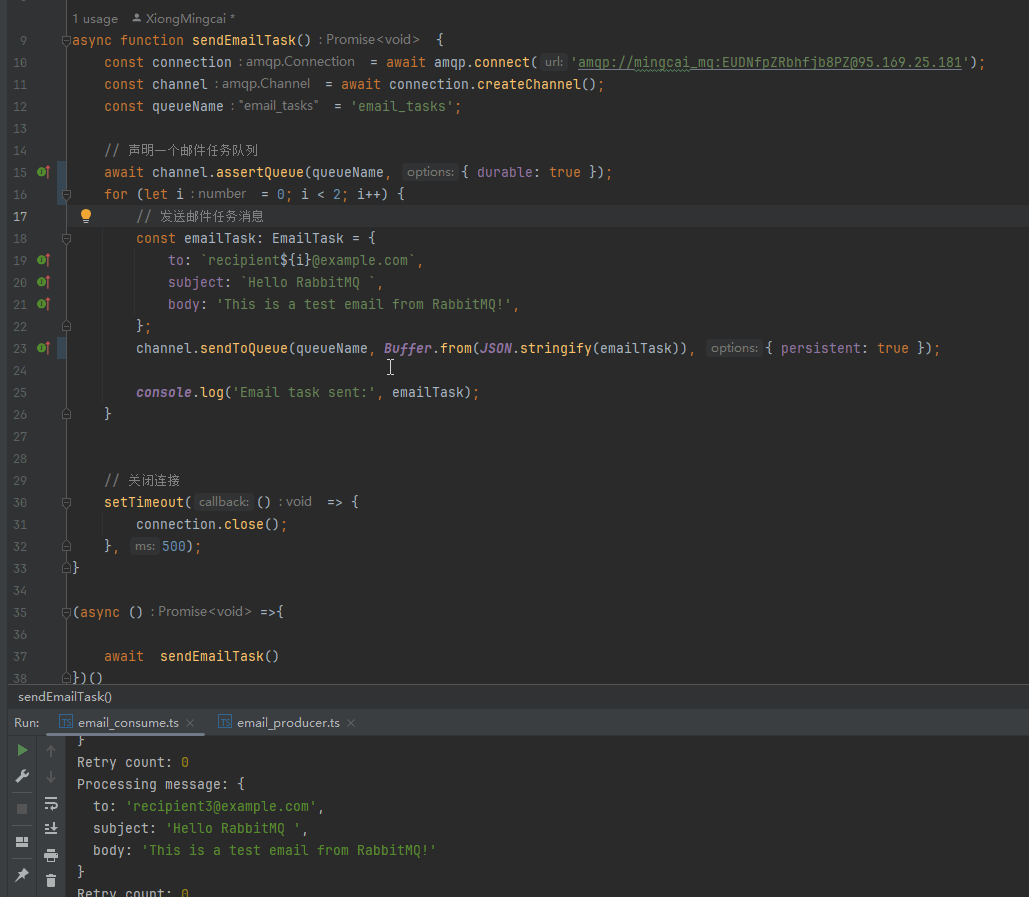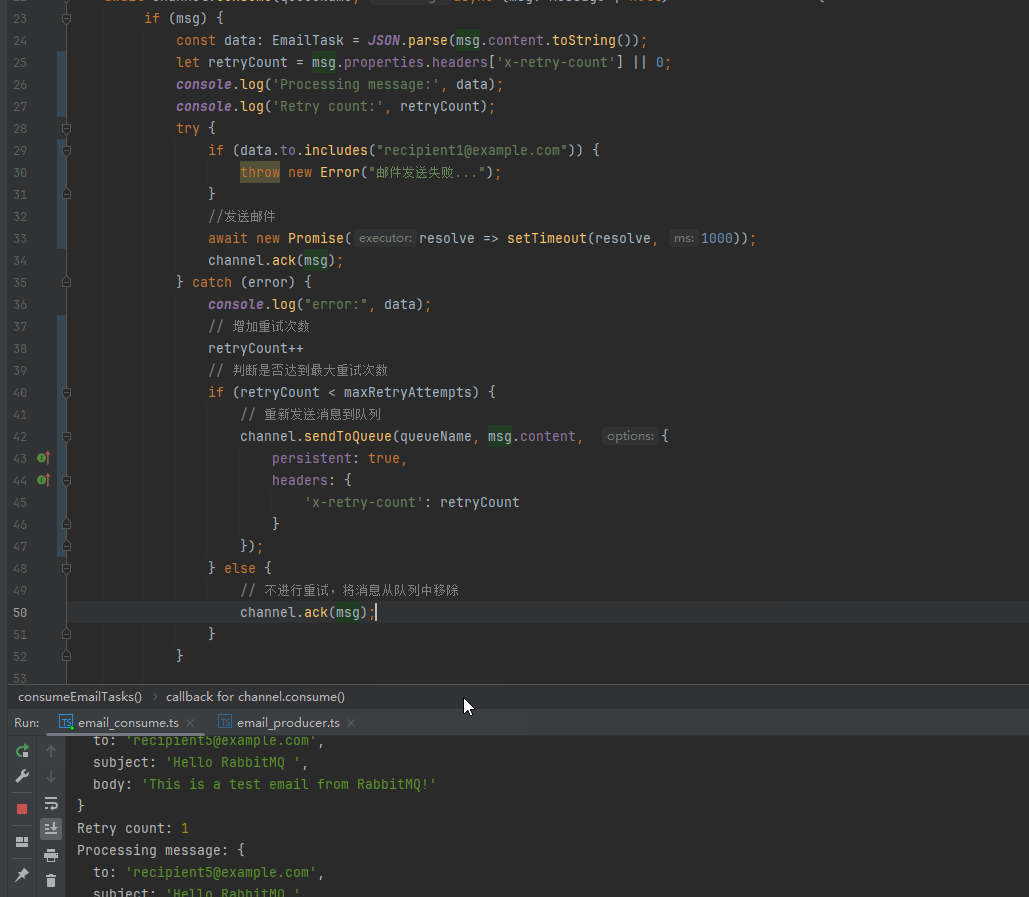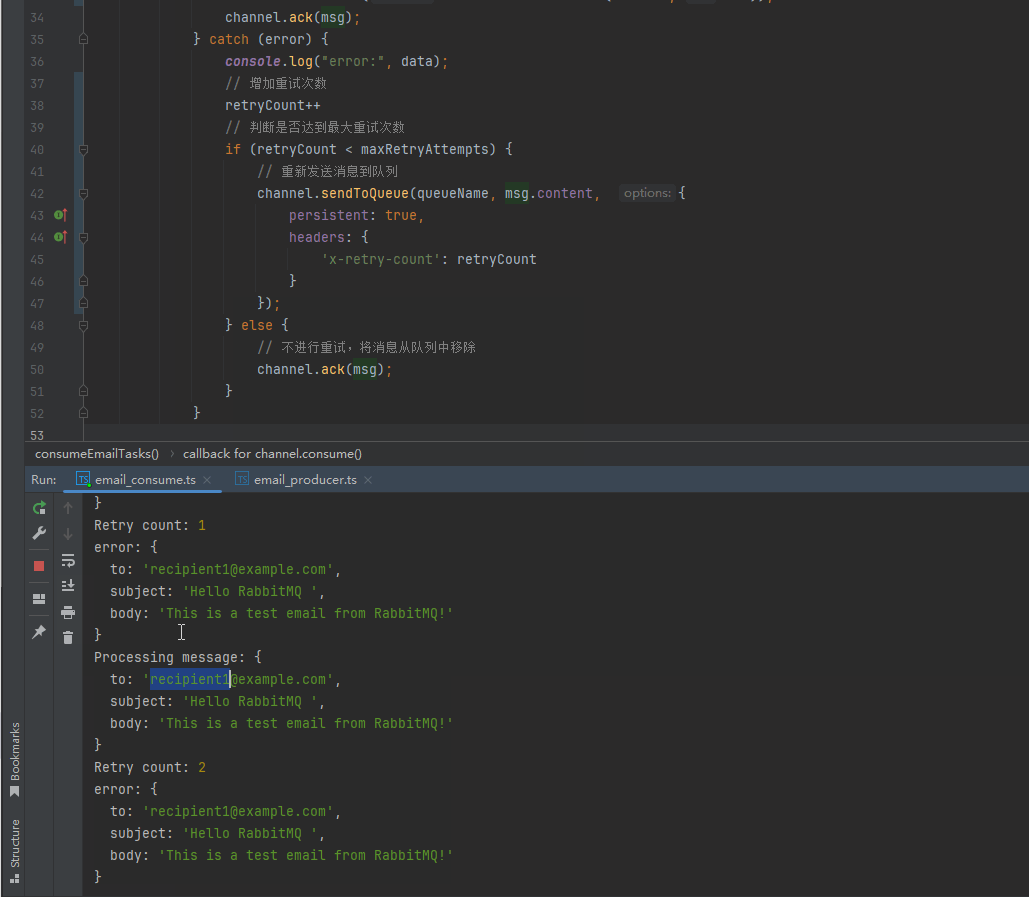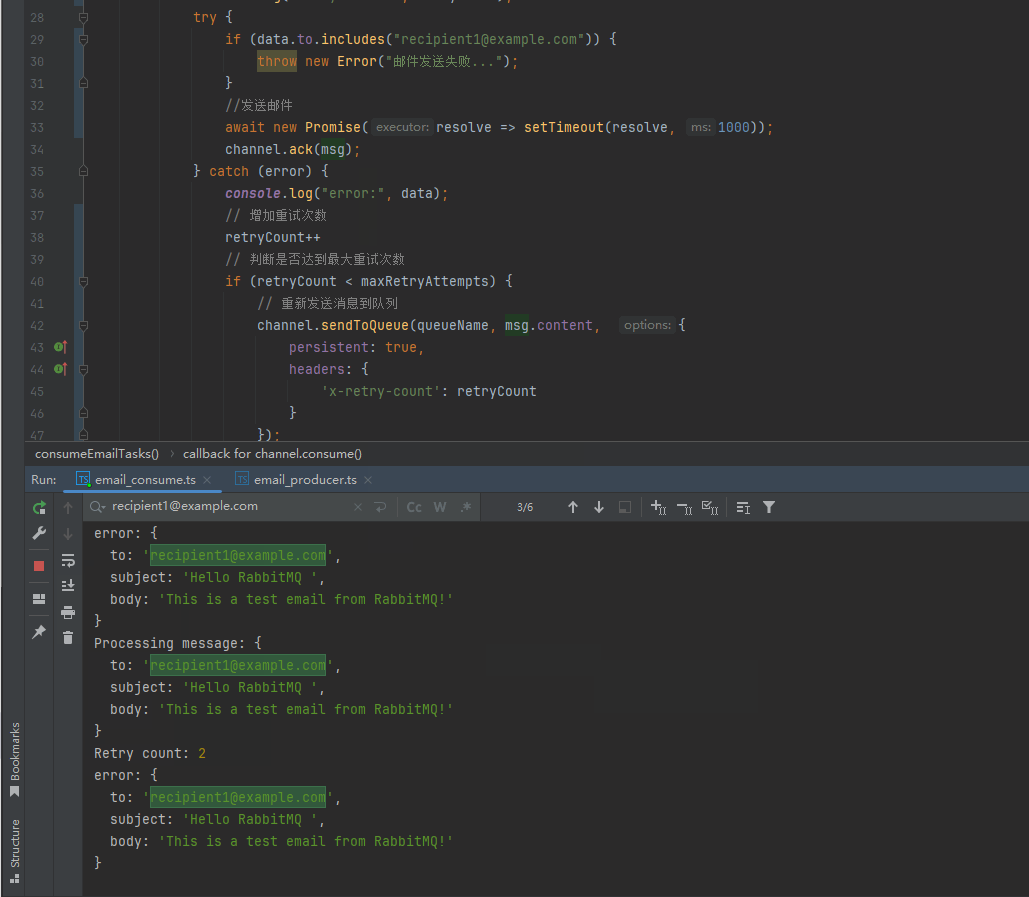
RabbitMQ简单模式和工作模式
RabbitMQ 是一个消息队列中间件,用于在分布式系统中进行消息传递。在 RabbitMQ 中,有几种工作模式,其中简单模式和工作模式是其中两种基本的模式之一。 简单模式(Simple Mode): 在简单模式中,有…...

c语言实战之贪吃蛇
文章目录 前言效果展示游戏用到的图片游戏思路一览游戏前准备一、贪吃蛇、食物、障碍物节点坐标的结构体二、枚举游戏状态、和贪吃蛇的方向三、维护运行的结构体 游戏开始前的初始化一、学习图形库相关知识二、设置背景三、欢迎界面四、初始化贪吃蛇五、生成障碍物六、生成食物…...
)
Midjourney图片生成描述词记录(今天一天)
抄别人的描述词 /imagine prompt:https://(你的图片地址).jpg Super handsome boy IP by pop mart , green suit, no hair, bald head, Scenes in spring , pastel color , mockup , fine luster , clean background ,3D render , Soft focus , oc , bl…...
类和对象 第五部分第四小节:赋值运算符重载
C编译器至少给一个类添加4个函数 1.默认构造函数无参,函数体为空 2.默认析构函数无参,函数体为空 3.默认拷贝沟早函数,对属性进行值拷贝 4.赋值运算符“operator”,对属性进行值拷贝 如果类中有属性指向堆区,做赋值操作…...
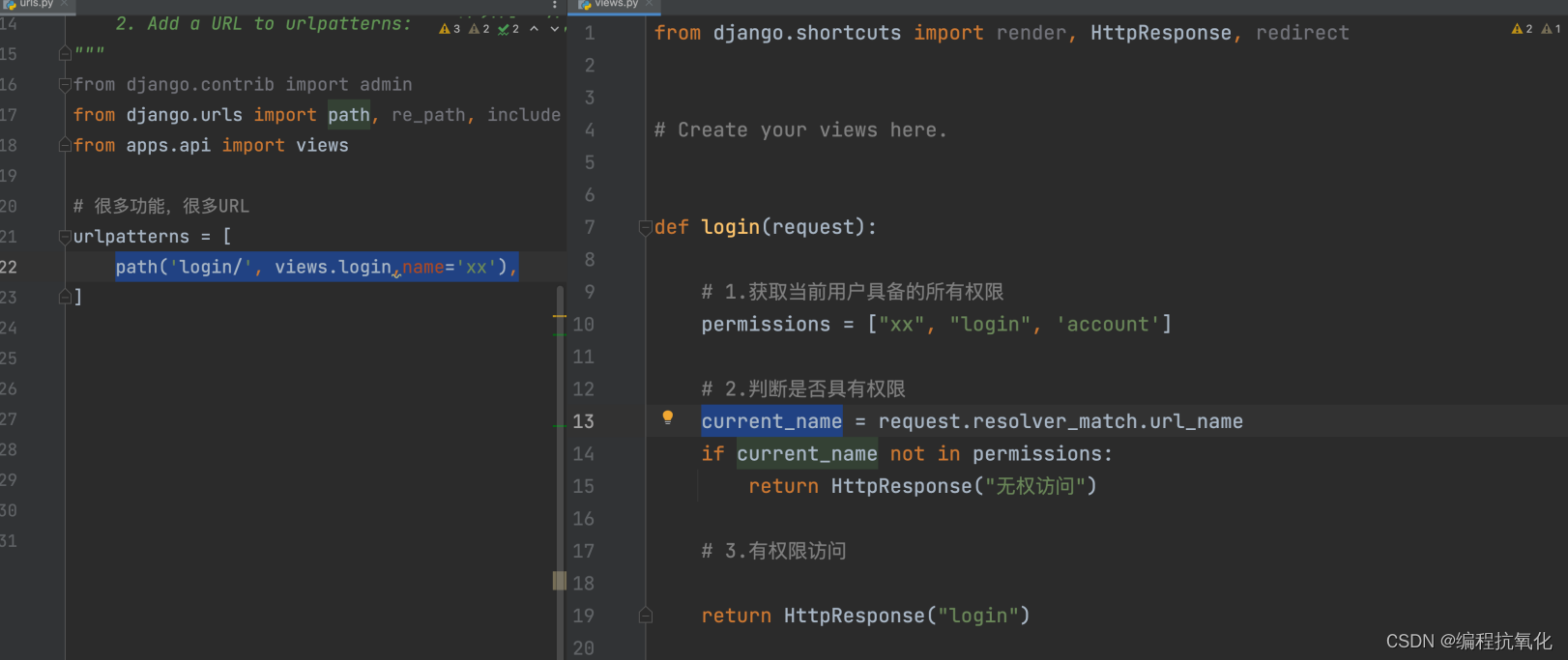
Django从入门到精通(一)
目录 一、Django环境搭建与命令 1.1、安装 1.2、命令行 创建项目 编写代码 运行 app概念 1.3、Pycharm创建项目 1.4、虚拟环境 创建虚拟环境 - 命令行 介绍 操作 基本问题 Pycharm 项目虚拟环境 django虚拟环境【安装django最新版本】 django虚拟环境【安装指…...

数据库分表分库的原则
什么是数据库分库分表 数据库分表(Table Sharding) 数据库分表是将一个大表按照某种规则拆分成多个小表存储在不同的物理表中的技术。通常,拆分规则是基于某个列的值进行拆分,例如根据用户ID或日期范围等进行拆分。每个小表只包…...
Java技术栈 —— Docker容器
Java技术栈 —— Docker容器 一、什么是Docker?二、如何安装Docker?三、如何使用Docker? 一、什么是Docker? docker的本意是码头工人。 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个…...
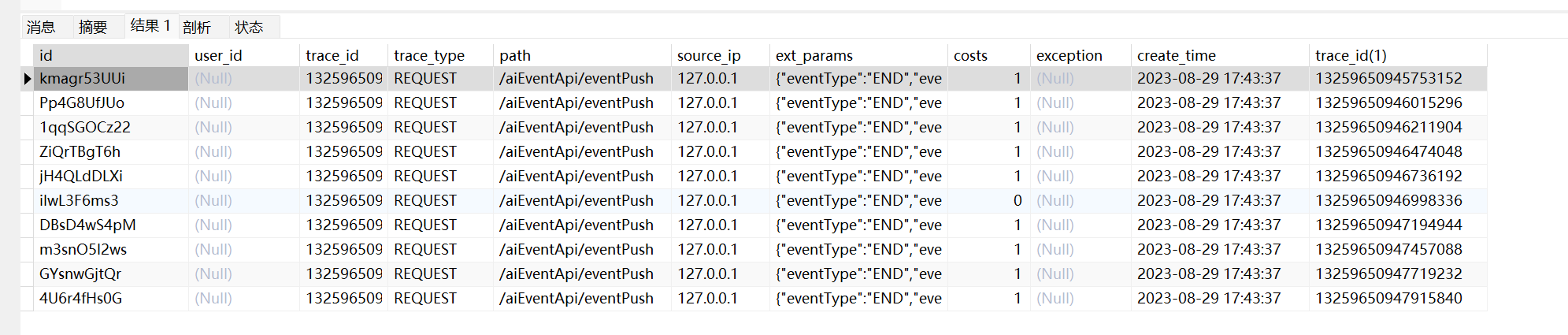
Mysql大数据量分页优化
前言 之前有看过到mysql大数据量分页情况下性能会很差,但是没有探究过它的原因,今天讲一讲mysql大数据量下偏移量很大,性能很差的问题,并附上解决方式。 原因 将原因前我们先做一个试验,我做试验使用的是mysql5.7.2…...

QT tcp与udp网络通信以及定时器的使用 (7)
QT tcp与udp网络通信以及定时器的使用 文章目录 QT tcp与udp网络通信以及定时器的使用1、QT网络与通信简单介绍2、QT TCP通信1、 服务器的流程2、 客户端的流程3、服务器的编写4、客户端的编写 3、QT UDP通信1、客户端流程2、客户端编写3、UDP广播4、UDP组播 4、定时器的用法1、…...

web架构师编辑器内容-添加自动保存的功能
对于频繁改动的应用,自动保存的功能是一个非常有用的功能,可以避免用户在没有保存的情况下丢失自己保存过的数据。 对于自动保存,一般有两种实现,参考语雀和石墨: 语雀采用的是定时保存的方式,大约在3分半…...

【Redis】关于它为什么快?使用场景?以及使用方式?为何引入多线程?
目录 1.既然redis那么快,为什么不用它做主数据库,只用它做缓存? 2.Redis 一般在什么场合下使用? 3.redis为什么这么快? 4.Redis为什么要引入了多线程? 1.既然redis那么快,为什么不用它做主数据…...
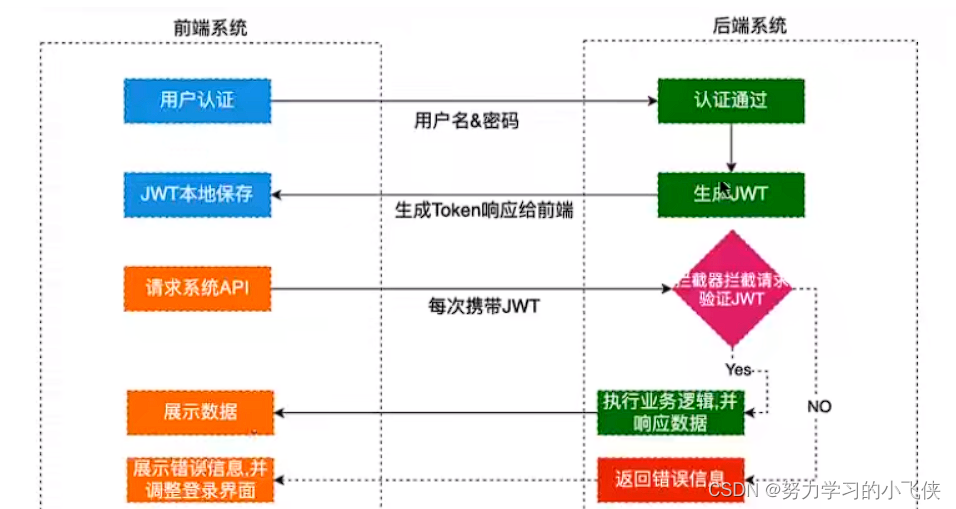
SpringBoot之JWT登录
JWT JSON Web Token(JSON Web令牌) 是一个开放标准(rfc7519),它定义了一种紧凑的、自包含的方式,用于在各方之间以JSON对象安全地传输信息。此信息可以验证和信任,因为它是数字签名的。jwt可以使用秘密〈使用HNAC算法…...

【备战蓝桥杯】——循环结构
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-bFHV3Dz5xMe6d3NB {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...

【数据分享】1929-2023年全球站点的逐年平均气温数据(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标,其中又以气温指标最为常用!说到气温数据,最详细的气温数据是具体到气象监测站点的气温数据!本次我们为大家带来的就是具体到气象监…...
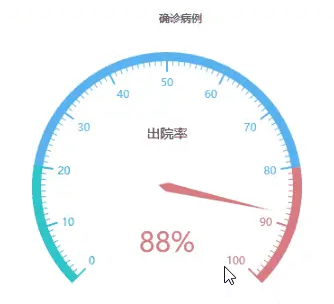
探索Pyecharts关系图绘制技巧:炫酷效果与创意呈现【第42篇—python:Pyecharts水球图】
文章目录 Pyecharts绘制多种炫酷关系网图引言准备工作代码实战1. 基本关系网图2. 自定义节点样式和边样式3. 关系网图的层级结构4. 添加标签和工具提示5. 动态关系网图6. 高级关系网图 - Les Miserables 示例7. 自定义关系网图布局8. 添加背景图9. 3D 关系网图10. 热力关系网图…...

蓝桥杯-循环节长度
两个整数做除法,有时会产生循环小数,其循环部分称为: 循环节。比如,11/136>0.8461553846153..... 其循环节为[846153] 共有 6 位。下面的方法,可以求出循环节的长度。请仔细阅读代码,并填写划线部分缺少的代码。 注…...

Jython调用openwire库连接activemq转发topic订阅消息到另一个activemq 服务器上 完整代码
以下是一个示例代码,演示如何在Jython中使用OpenWire库连接ActiveMQ,将一个主题(topic)上的订阅消息转发到另一个ActiveMQ服务器上: from org.apache.activemq import * from org.apache.activemq.transport import *…...

面试经典题---30.串联所有单词的子串
30.串联所有单词的子串 我的解法: 滑动窗口: 解法中用到了两个哈希表map1和map2,分别用于记录words中各个单词的出现频数和当前滑动窗口[left, right)中单词的出现频数;外部for循环i从0到len - 1,内部while循环每次会…...
-Kimen(奇门))
字符串随机生成工具(开源)-Kimen(奇门)
由于最近笔者在开发数据脱敏相关功能,其中一类脱敏需求为能够按照指定的格式随机生成一个字符串来代替原有信息,数据看起来格式需要与原数据相同,如:电话号码,身份证号以及邮箱等。在网上搜索了下,发现没有…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
