瑞_数据结构与算法_AVL树
文章目录
- 1 什么是AVL树
- 1.1 AVL树的背景及定义
- 1.2 判断失衡
- 1.2.1 平衡因子
- 1.2.2 失衡的四种情况
- 1.2.2.1 LL
- 1.2.2.2 LR
- 1.2.2.3 RL
- 1.2.2.4 RR
- 1.3 解决失衡
- 1.3.1 左旋(RR)
- 1.3.2 右旋(LL)
- 1.3.3 先左旋再右旋(LR)
- 1.3.4 先右旋再左旋(RL)
- 1.4 AVL树的优缺点
- 1.4.1 AVL树的优点
- 1.4.2 AVL树的缺点
- 2 AVL树的Java实现
- 2.1 AVL树节点类AVLNode
- 2.2 实现求任意节点高度方法height(AVLNode node)
- 2.3 实现更新节点高度方法updateHeight(AVLNode node)
- 2.4 实现求平衡因子方法bf(AVLNode node)
- 2.5 实现右旋方法rightRotate(AVLNode red)
- 2.6 实现左旋方法leftRotate(AVLNode red)
- 2.7 实现先左旋再右旋方法leftRightRotate(AVLNode node)
- 2.8 实现先右旋再左旋方法rightLeftRotate(AVLNode node)
- 2.9 实现判断及调整平衡方法balance(AVLNode node) ★
- 2.10 实现新增方法put(int key, Object value)
- 2.11 实现删除方法remove(int key)
- 3 AVL树Java实现代码完整版(复制粘贴用)
🙊前言:本文章为瑞_系列专栏之《数据结构与算法》的AVL树篇。由于博主是从B站黑马程序员的《数据结构与算法》学习到的相关知识,所以本系列专栏主要针对该课程进行笔记总结和拓展,文中的部分原理及图解也是来源于黑马提供的资料。本文仅供大家交流、学习及研究使用,禁止用于商业用途,违者必究!

1 什么是AVL树
1.1 AVL树的背景及定义
AVL 树是一种自平衡二叉搜索树,由托尔·哈斯特罗姆在 1960 年提出并在 1962 年发表。它的名字来源于发明者的名字:Adelson-Velsky 和 Landis,他们是苏联数学家,于 1962 年发表了一篇论文,详细介绍了 AVL 树的概念和性质。
在二叉搜索树中,如果插入的元素按照特定的顺序排列,可能会导致树变得非常不平衡,从而降低搜索、插入和删除的效率。
瑞:关于二叉搜索树的相关知识,可以参考《瑞_数据结构与算法_二叉搜索树》
为了解决这个问题,AVL 树通过在每个节点中维护一个平衡因子来确保树的平衡。平衡因子是左子树的高度减去右子树的高度。如果平衡因子的绝对值大于等于 2,则通过旋转操作来重新平衡树。
由于二叉搜索树在插入和删除时,节点可能失衡,诞生了AVL 树,如果在插入和删除时通过旋转, 始终让二叉搜索树保持平衡, 称为自平衡的二叉搜索树,AVL 是自平衡二叉搜索树的实现之一。
AVL 树是用于存储有序数据的一种重要数据结构,它是二叉搜索树的一种改进和扩展。它不仅能够提高搜索、插入和删除操作的效率,而且还能够确保树的深度始终保持在 O(log n) 的水平。随着计算机技术的不断发展,AVL 树已经成为了许多高效算法和系统中必不可少的一种基础数据结构。
如果一棵二叉搜索树长的不平衡,那么查询的效率会受到影响,如下二叉树所示,如果要搜索1,则需要比较3次,效率很低
3(高度3)/2(高度2)/1(高度1)
通过旋转可以让树重新变得平衡,并且不会改变二叉搜索树的性质(即左边仍然小,右边仍然大)
上面的二叉树根节点高度是3,右孩子为null,可以认为高度为0,所以高度差3-0=3>1,将上面的二叉树进行右旋后,如下所示,最多只要比较2次,效率提升
2(高度2)/ \1(高度1) 3(高度1)
瑞:注意旋转是不会破坏二叉树的性质的,左边小,右边大
1.2 判断失衡
如果一个节点的左右孩子,高度差超过 1,则此节点失衡,才需要旋转。失衡的情况发生在二叉树的新增和删除操作的时候。
瑞:关于二叉搜索树的高度,可以参考《瑞_数据结构与算法_二叉搜索树》。高度如下图所示,注意如果某节点为null,则将该节点的高度视作0。

1.2.1 平衡因子
由于判断失衡的条件为:一个节点的左右孩子,高度差超过 1,所以定义平衡因子(balance factor)简写bf,如下:
平衡因子 = 左子树高度 - 右子树高度

上图二叉树中
- 对于节点2,左孩子节点1(高度为1)和右孩子节点4(高度为2)的高度差为-1,表示左右平衡
- 对于节点4,左孩子节点3(高度为1)和右孩子节点5(高度为1)的高度差为0,表示左右平衡
如果修改如下:
2(高度2)\4(高度1)
上图二叉树中,对于节点2,左孩子节点null(高度为0)和右孩节点4(高度为1)的高度差为1,表示左右平衡
继续修改如下:
3(高度3)/2(高度2)/1(高度1)
上图二叉树中,对于节点3,左孩子节点2(高度为2)和右孩节点null(高度为0)高度差为2>1,表示左边太高
继续修改如下:
2(高度3)\4(高度2)\5(高度1)
上图二叉树中,对于节点2,左孩子节点null(高度为0)和右孩节点4(高度为2)高度差为-2<-1,表示右边太高
所以当平衡因子
- bf = 0,1,-1 时,表示左右平衡
- bf > 1 时,表示左边太高
- bf < -1 时,表示右边太高
瑞:不取绝对值就是为了区分是左边高还是右边高
1.2.2 失衡的四种情况
通过前人的经验总结,失衡的情况一共有LL、LR、RL、RR四种情况。
1.2.2.1 LL
bf > 1 && bf(node.left) >= 0为LL情况,如下图所示:
- 失衡节点(图中 5 红色)的 bf > 1,即左边更高
- 失衡节点的左孩子(图中 3 黄色)的 bf >= 0 即左孩子这边也是左边更高或等高

1.2.2.2 LR
bf > 1 && bf(node.left) < 0为LR情况,如下图所示:
- 失衡节点(图中 6 )的 bf > 1,即左边更高
- 失衡节点的左孩子(图中 2 红色)的 bf < 0 即左孩子这边是右边更高

1.2.2.3 RL
与LR对称的情况,bf < -1 && bf(node.right) > 0为RL情况,如下图所示:
- 失衡节点(图中 2)的 bf <-1,即右边更高
- 失衡节点的右孩子(图中 6 红色)的 bf > 0,即右孩子这边左边更高

1.2.2.4 RR
与LL对称的情况,bf < -1 && bf(node.right) <= 0为RL情况,如下图所示:
- 失衡节点(图中 2 红色)的 bf <-1,即右边更高
- 失衡节点的右孩子(图中 4 黄色)的 bf <= 0,即右孩子这边右边更高或等高

1.3 解决失衡
失衡可以通过树的旋转解决。
树的旋转是:在不干扰元素顺序的情况下更改结构,通常用来让树的高度变得平衡。
1.3.1 左旋(RR)
RR情况通过一次左旋即可恢复平衡

如上图,对于节点2,左孩子节点1的高度为1,右孩子节点4的高度为3,高度差为1-3=-2<-1,所以右边太高,应当向左旋转,降低右边高度。
进行左旋需要操作的节点有4、2、3,对2进行左旋后,4变为根节点,2变为其左子树,而原来4的左子树节点3要更改为节点2的右子树(换爹)。
向左旋转后的结果如下图所示:

1.3.2 右旋(LL)
LL情况通过一次右旋即可恢复平衡

如上图,对于节点5,左孩子节点3的高度为3,右孩子节点6的高度为1,高度差为3-1=2>1,所以左边太高,应当向右旋转,降低左边高度。
进行右旋需要操作的节点有5、3、4,对5进行右旋后,3变为根节点,5变为其右子树,而原来3的右子树节点4要更改为节点5的左子树(换爹)。
向右旋转后的结果如下图所示:

1.3.3 先左旋再右旋(LR)
LR情况需要先让左子树向左
旋转,变为LL的情况,然后再向右旋转,恢复平衡

如上图,对节点6的左子树(4,2,3)进行左旋,变为LL的情况,如下图:

再对其进行右旋就恢复平衡,如下图:

1.3.4 先右旋再左旋(RL)
RL情况需要先让右子树向右
旋转,变为RR的情况,然后再向左旋转,恢复平衡

如上图,对节点2的右子树(4,6,5)进行右旋,变为RR的情况,如下图:

再对其进行左旋就恢复平衡,如下图:

1.4 AVL树的优缺点
1.4.1 AVL树的优点
- AVL树是一种自平衡树,保证了树的高度平衡,从而保证了树的查询和插入操作的时间复杂度均为O(logn)。
- 相比于一般二叉搜索树,AVL树对查询效率的提升更为显著,因为其左右子树高度的差值不会超过1,避免了二叉搜索树退化为链表的情况,使得整棵树的高度更低。
- AVL树的删除操作比较简单,只需要像插入一样旋转即可,在旋转过程中树的平衡性可以得到维护。
1.4.2 AVL树的缺点
- AVL树每次插入或删除节点时需要进行旋转操作,这个操作比较耗时,因此在一些应用中不太适用。
- 在AVL树进行插入或删除操作时,为保持树的平衡需要不断进行旋转操作,在一些高并发环节和大数据量环境下,这可能会导致多余的写锁导致性能瓶颈。
- AVL树的旋转操作相对较多,因此在一些应用中可能会造成较大的空间浪费。
2 AVL树的Java实现
1️⃣内部节点类AVLNode中含有属性:
- 索引
- 存储值
- 左孩子
- 右孩子
- 节点高度
2️⃣AVLTree二叉搜索树类含有方法:
- 求任意节点高度height(AVLNode node)
- 更新节点高度updateHeight(AVLNode node)
- 求平衡因子bf(AVLNode node)
- 右旋rightRotate(AVLNode red)
- 左旋leftRotate(AVLNode red)
- 先左旋再右旋leftRightRotate(AVLNode node)
- 先右旋再左旋rightLeftRotate(AVLNode node)
- 判断及调整平衡balance(AVLNode node)
- 新增put(int key, Object value)
- 删除remove(int key)
2.1 AVL树节点类AVLNode
/*** <h3>AVL 树</h3>* <ul>* <li>二叉搜索树在插入和删除时,节点可能失衡</li>* <li>如果在插入和删除时通过旋转, 始终让二叉搜索树保持平衡, 称为自平衡的二叉搜索树</li>* <li>AVL 是自平衡二叉搜索树的实现之一</li>* </ul>*/
public class AVLTree {static class AVLNode {/*** 索引*/int key;/*** 存储值*/Object value;/*** 左孩子*/AVLNode left;/*** 右孩子*/AVLNode right;/*** 节点高度,初始默认为1*/int height = 1;public AVLNode(int key, Object value) {this.key = key;this.value = value;}public AVLNode(int key) {this.key = key;}public AVLNode(int key, Object value, AVLNode left, AVLNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}
}
2.2 实现求任意节点高度方法height(AVLNode node)
height(AVLNode node)方法为查找该节点在AVL树中的高度
虽然已经在AVLNode节点类中已经有了高度属性,但是也有可能传入null,null不可能去调用属性height,所以要特别定义方法进行处理,实现很简单如下:
// 求任意节点高度private int height(AVLNode node) {return node == null ? 0 : node.height;}
2.3 实现更新节点高度方法updateHeight(AVLNode node)
updateHeight(AVLNode node)方法为私有方法,因为将来新增、删除、旋转时,高度都可能发生变化,需要内部调用本方法更新高度值。
思路:取该节点的左孩子和右孩子中索引更大的一个值,高度+1的结果则为该节点的高度(如果孩子节点为null,则高度视作0)
下面是更新高度的代码:
// 更新节点高度 (新增、删除、旋转)private void updateHeight(AVLNode node) {node.height = Integer.max(height(node.left), height(node.right)) + 1;}
求一个节点左右子树的高度差
2.4 实现求平衡因子方法bf(AVLNode node)
bf(AVLNode node)方法为私有方法,因为判断失衡需要用到平衡因子。
平衡因子 (balance factor) = 左子树高度-右子树高度
本方法返回一个整数,含义如下:
- bf = 0,1,-1 时,表示左右平衡
- bf > 1 时,表示左边太高
- bf < -1 时,表示右边太高
/*** 平衡因子 (balance factor) = 左子树高度-右子树高度** @param node 要计算平衡因子的节点类* @return 平衡因子值* - bf = 0,1,-1 时,表示左右平衡* - bf > 1 时,表示左边太高* - bf < -1 时,表示右边太高**/private int bf(AVLNode node) {return height(node.left) - height(node.right);}
2.5 实现右旋方法rightRotate(AVLNode red)
向右旋转前,如下图所示:

- 红色节点,旧根(失衡节点)
- 黄色节点,旧根的左孩子,将来作为新根,旧根是它右孩子
- 绿色节点,新根的右孩子,将来要换爹作为旧根的左孩子
右旋后,如下图所示:

实现代码如下:
/*** 右旋** @param red 要旋转的节点* @return 新的根节点**/private AVLNode rightRotate(AVLNode red) {AVLNode yellow = red.left;AVLNode green = yellow.right;yellow.right = red; // 上位(旋转)red.left = green; // 换爹updateHeight(red); // 更新高度updateHeight(yellow); // 更新高度return yellow;}
由于是右旋操作,左子树肯定比右子树高,所以黄色节点不可能为null,也就是yellow.right不会报空指针异常,无需判断。只有红色和黄色节点的高度会发生变化,所以更新高度只需要更新红色节点和黄色节点。
2.6 实现左旋方法leftRotate(AVLNode red)
向左旋转前,如下图所示:

- 红色节点,旧根(失衡节点)
- 黄色节点,旧根的右孩子,将来作为新根,旧根是它左孩子
- 绿色节点,新根的左孩子,将来要换爹作为旧根的右孩子
左旋后,如下图所示:

实现代码如下:
/*** 左旋** @param red 要旋转的节点* @return 新的根节点**/private AVLNode leftRotate(AVLNode red) {AVLNode yellow = red.right;AVLNode green = yellow.left;yellow.left = red; // 上位red.right = green; // 换爹updateHeight(red); // 更新高度updateHeight(yellow); // 更新高度return yellow;}
只有红色和黄色节点的高度会发生变化,所以更新高度只需要更新红色节点和黄色节点。
2.7 实现先左旋再右旋方法leftRightRotate(AVLNode node)
先让左子树调用左旋方法,变为LL的情况,然后再调用右旋方法,恢复平衡
// 先左旋左子树, 再右旋根节点private AVLNode leftRightRotate(AVLNode node) {node.left = leftRotate(node.left);return rightRotate(node);}
2.8 实现先右旋再左旋方法rightLeftRotate(AVLNode node)
先让右子树调用右旋方法,变为RR的情况,然后再调用左旋方法,恢复平衡
// 先右旋右子树, 再左旋根节点private AVLNode rightLeftRotate(AVLNode node) {node.right = rightRotate(node.right);return leftRotate(node);}2.9 实现判断及调整平衡方法balance(AVLNode node) ★
balance(AVLNode node)是为了检查节点是否失衡,重新平衡。是比较重要的综合性方法。
// 检查节点是否失衡, 重新平衡代码private AVLNode balance(AVLNode node) {if (node == null) {return null;}int bf = bf(node);if (bf > 1 && bf(node.left) >= 0) { // LLreturn rightRotate(node);} else if (bf > 1 && bf(node.left) < 0) { // LRreturn leftRightRotate(node);} else if (bf < -1 && bf(node.right) > 0) { // RLreturn rightLeftRotate(node);} else if (bf < -1 && bf(node.right) <= 0) { // RRreturn leftRotate(node);}return node;}
注意LL和RR的删除情况,所以要考虑等于0的情况。以上四种旋转代码里,都需要更新高度,需要更新的节点是红色、黄色,而绿色节点高度不变
2.10 实现新增方法put(int key, Object value)
/*** 根节点*/AVLNode root;/*** 新增节点 - 递归实现** @param key 索引* @param value 存储值**/public void put(int key, Object value) {root = doPut(root, key, value);}private AVLNode doPut(AVLNode node, int key, Object value) {// 1. 找到空位, 创建新节点if (node == null) {return new AVLNode(key, value);}// 2. key 已存在, 更新if (key == node.key) {node.value = value;return node;}// 3. 继续查找if (key < node.key) {node.left = doPut(node.left, key, value); // 向左} else {node.right = doPut(node.right, key, value); // 向右}// 以下为AVL树和二叉树的新增区别,需要更新高度,判断平衡updateHeight(node);return balance(node);}
2.11 实现删除方法remove(int key)
/*** 删除节点 - 递归实现** @param key 要删除节点的索引值**/public void remove(int key) {root = doRemove(root, key);}private AVLNode doRemove(AVLNode node, int key) {// 1. node == nullif (node == null) {return null;}// 2. 没找到 keyif (key < node.key) {node.left = doRemove(node.left, key);} else if (node.key < key) {node.right = doRemove(node.right, key);} else {// 3. 找到 key 1) 没有孩子 2) 只有一个孩子 3) 有两个孩子if (node.left == null && node.right == null) {return null;} else if (node.left == null) {node = node.right;} else if (node.right == null) {node = node.left;} else {AVLNode s = node.right;while (s.left != null) {s = s.left;}// s 后继节点s.right = doRemove(node.right, s.key);s.left = node.left;node = s;}}// 4. 更新高度updateHeight(node);// 5. balancereturn balance(node);}
3 AVL树Java实现代码完整版(复制粘贴用)
/*** <h3>AVL 树</h3>* <ul>* <li>二叉搜索树在插入和删除时,节点可能失衡</li>* <li>如果在插入和删除时通过旋转, 始终让二叉搜索树保持平衡, 称为自平衡的二叉搜索树</li>* <li>AVL 是自平衡二叉搜索树的实现之一</li>* </ul>*/
public class AVLTree {static class AVLNode {/*** 索引*/int key;/*** 存储值*/Object value;/*** 左孩子*/AVLNode left;/*** 右孩子*/AVLNode right;/*** 节点高度,初始默认为1*/int height = 1;public AVLNode(int key, Object value) {this.key = key;this.value = value;}public AVLNode(int key) {this.key = key;}public AVLNode(int key, Object value, AVLNode left, AVLNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}/*** 根节点*/AVLNode root;// 求任意节点高度private int height(AVLNode node) {return node == null ? 0 : node.height;}// 更新节点高度 (新增、删除、旋转)private void updateHeight(AVLNode node) {node.height = Integer.max(height(node.left), height(node.right)) + 1;}/*** 平衡因子 (balance factor) = 左子树高度-右子树高度** @param node 要计算平衡因子的节点类* @return 平衡因子值* - bf = 0,1,-1 时,表示左右平衡* - bf > 1 时,表示左边太高* - bf < -1 时,表示右边太高**/private int bf(AVLNode node) {return height(node.left) - height(node.right);}/*** 右旋** @param red 要旋转的节点* @return 新的根节点**/private AVLNode rightRotate(AVLNode red) {AVLNode yellow = red.left;AVLNode green = yellow.right;yellow.right = red; // 上位red.left = green; // 换爹updateHeight(red);updateHeight(yellow);return yellow;}/*** 左旋** @param red 要旋转的节点* @return 新的根节点**/private AVLNode leftRotate(AVLNode red) {AVLNode yellow = red.right;AVLNode green = yellow.left;yellow.left = red; // 上位red.right = green; // 换爹updateHeight(red);updateHeight(yellow);return yellow;}// 先左旋左子树, 再右旋根节点private AVLNode leftRightRotate(AVLNode node) {node.left = leftRotate(node.left);return rightRotate(node);}// 先右旋右子树, 再左旋根节点private AVLNode rightLeftRotate(AVLNode node) {node.right = rightRotate(node.right);return leftRotate(node);}// 检查节点是否失衡, 重新平衡代码private AVLNode balance(AVLNode node) {if (node == null) {return null;}int bf = bf(node);if (bf > 1 && bf(node.left) >= 0) { // LLreturn rightRotate(node);} else if (bf > 1 && bf(node.left) < 0) { // LRreturn leftRightRotate(node);} else if (bf < -1 && bf(node.right) > 0) { // RLreturn rightLeftRotate(node);} else if (bf < -1 && bf(node.right) <= 0) { // RRreturn leftRotate(node);}return node;}/*** 新增节点 - 递归实现** @param key 索引* @param value 存储值**/public void put(int key, Object value) {root = doPut(root, key, value);}private AVLNode doPut(AVLNode node, int key, Object value) {// 1. 找到空位, 创建新节点if (node == null) {return new AVLNode(key, value);}// 2. key 已存在, 更新if (key == node.key) {node.value = value;return node;}// 3. 继续查找if (key < node.key) {node.left = doPut(node.left, key, value); // 向左} else {node.right = doPut(node.right, key, value); // 向右}updateHeight(node);return balance(node);}/*** 删除节点 - 递归实现** @param key 要删除节点的索引值**/public void remove(int key) {root = doRemove(root, key);}private AVLNode doRemove(AVLNode node, int key) {// 1. node == nullif (node == null) {return null;}// 2. 没找到 keyif (key < node.key) {node.left = doRemove(node.left, key);} else if (node.key < key) {node.right = doRemove(node.right, key);} else {// 3. 找到 key 1) 没有孩子 2) 只有一个孩子 3) 有两个孩子if (node.left == null && node.right == null) {return null;} else if (node.left == null) {node = node.right;} else if (node.right == null) {node = node.left;} else {AVLNode s = node.right;while (s.left != null) {s = s.left;}// s 后继节点s.right = doRemove(node.right, s.key);s.left = node.left;node = s;}}// 4. 更新高度updateHeight(node);// 5. balancereturn balance(node);}
}
如果觉得这篇文章对您有所帮助的话,请动动小手点波关注💗,你的点赞👍收藏⭐️转发🔗评论📝都是对博主最好的支持~
相关文章:

瑞_数据结构与算法_AVL树
文章目录 1 什么是AVL树1.1 AVL树的背景及定义1.2 判断失衡1.2.1 平衡因子1.2.2 失衡的四种情况1.2.2.1 LL1.2.2.2 LR1.2.2.3 RL1.2.2.4 RR 1.3 解决失衡1.3.1 左旋(RR)1.3.2 右旋(LL)1.3.3 先左旋再右旋(LR࿰…...

BGP同步规则
BGP同步规则:开启同步下,从IBGP收到一条路由不会传给任何EBGP邻居(实验效果IBGP邻居和EBGP邻居都不传),除非从自身的IGP中也学到这条路由。目的是防止AS内部出现路由黑洞,向外部通告了一个本AS不可达的虚假的路由。 同步规则只影响从IBGP邻居收到的路由,不影响从EBGP邻居收…...
)
Linux命令-apt-key命令(管理Debian Linux系统中的软件包密钥)
补充说明 apt-key命令 用于管理Debian Linux系统中的软件包密钥。每个发布的deb包,都是通过密钥认证 的,apt-key用来管理密钥。 语法 apt-key(参数)参数 操作指令:APT密钥操作指令。 实例 apt-key list # 列出已保存在系统中key。 apt-…...

Python根据Excel表进行文件重命名
一、问题背景 在日常办公过程中,批量重命名是经常使用的操作。之前我们已经进行了初步探索,主要是通过批处理文件、renamer软件或者Python中的pathlib等模块对当前目录下的文件进行批量重命名。 而今天我们要使用的是PythonExcel的方法对指定目录下的文…...
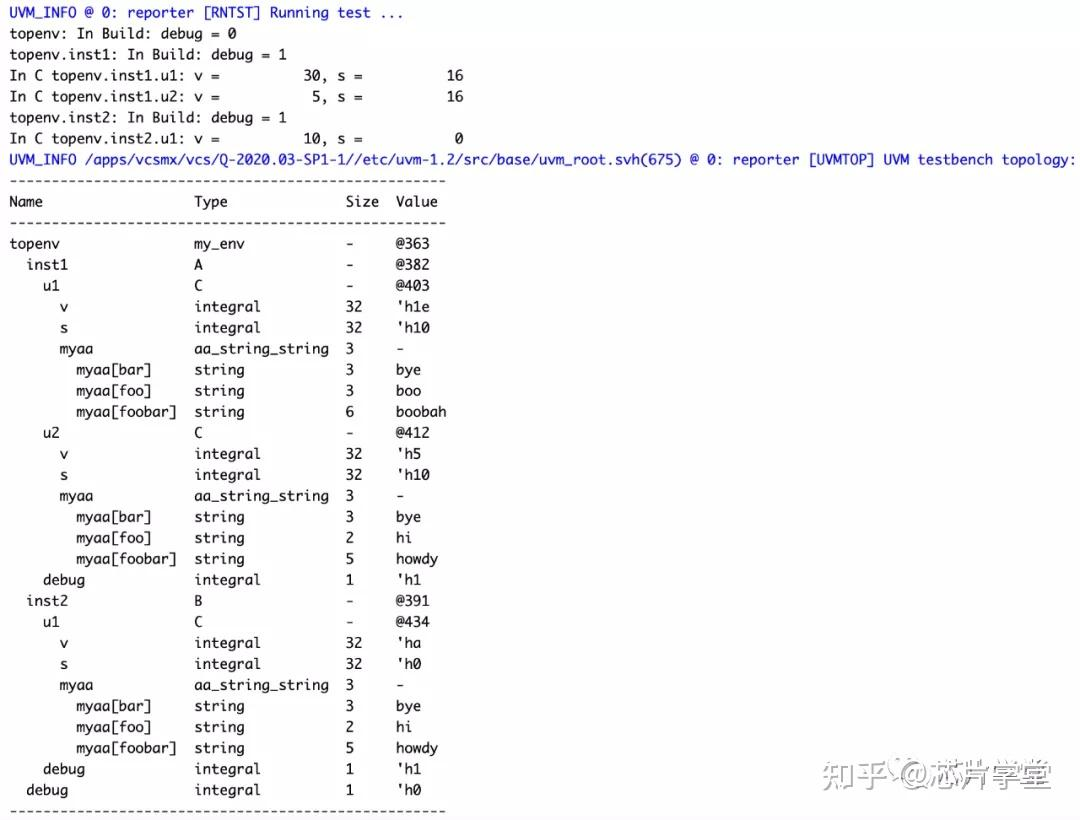
【UVM源码】UVM Config_db机制使用总结与源码解析
UVM Config_db机制使用总结与源码解析 UVM Config_db机制介绍UVM Config_db 机制引入的背景基本介绍使用方法优缺点: UVM Config_db机制使用示例:UVM Config_db使用高阶规则Config_db资源优先级 UVM Config_db 源码解析 UVM Config_db机制介绍 UVM Conf…...
群辉开启WebDav服务+cpolar内网穿透实现移动端ES文件浏览器远程访问本地NAS文件
文章目录 1. 安装启用WebDAV2. 安装cpolar3. 配置公网访问地址4. 公网测试连接5. 固定连接公网地址6. 使用固定地址测试连接 本文主要介绍如何在群辉中开启WebDav服务,并结合cpolar内网穿透工具生成的公网地址,通过移动客户端ES文件浏览器即可实现移动设…...

通过mybatis拦截器给sql执行加一个耗时监控
代码没什么内容,直接贴上来吧,其中costTimeUtil可以看我的另一篇博文:java实现一个不带次数变量的加权平均值算法-CSDN博客 Slf4j Intercepts({Signature(type StatementHandler.class,method "query",args {Statement.class, …...
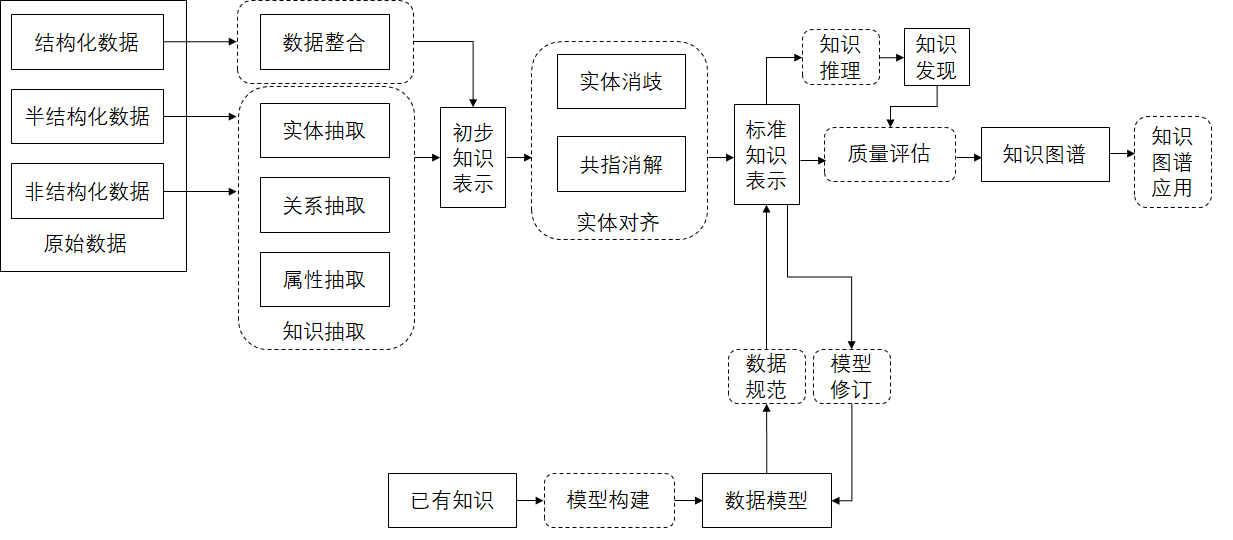
构建知识图谱:从技术到实战的完整指南
目录 一、概述二、知识图谱的基础理论定义与分类核心组成历史与发展 三、知识获取与预处理数据源选择数据清洗实体识别 四、知识表示方法知识表示模型RDFOWL属性图模型 本体构建关系提取与表示 五、知识图谱构建技术图数据库选择Neo4jArangoDB 构建流程数据预处理实体关系识别图…...

STM32的分类和选型
F系列(主要用于普通应用) STM32F0xx:低成本、低功耗,适用于成本敏感和低功耗的应用。STM32F1xx:中低端微控制器,具有丰富的外设和良好的性能。STM32F2xx:高性能微控制器,适用于要求…...

python使用read_sql与to_sql读写数据库
文章目录 详细说明示例程序 详细说明 使用pandas读写数据库的方法(以Mysql为例)如下: 首先是打包一个工具函数: import pandas as pd import numpy as np from sqlalchemy import create_engine, textdef get_sql_engine():# 数据…...

【ArcGIS微课1000例】0096:dem三维块状表达(层次地形模型)
文章目录 一、DEM表达方式二、层次模型表达三、注意事项一、DEM表达方式 DEM数字高程模型的表达方式通常有以下4种: 1. 规则格网 2. 不规则三角网 3. 等高线 4. 层次地形模型 作为栅格地理数据,DEM 数据具有2.5维的特征,能够以三维表面的形式进行三维空间表达。但受其数…...

OJ_糖果分享游戏
题干 c实现 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<vector> using namespace std;void ShareCandy(vector<int>& student) {int size student.size();vector<int> share(size); //保存每个同学交换前,糖果数量…...
sqli-lbs靶场搭建
目录 环境小皮源码下载 1.源码解压: 2.搭建网站 2.1点击创建网站 2.2修改sql-connections\db-creds.inc 2.3重新启动 3.访问你设置的域名 3.1点击启动数据库配置 3.2返回第一个页面(开启题目) sqlilbs靶场搭建 环境小皮源码下载 下载地址&am…...
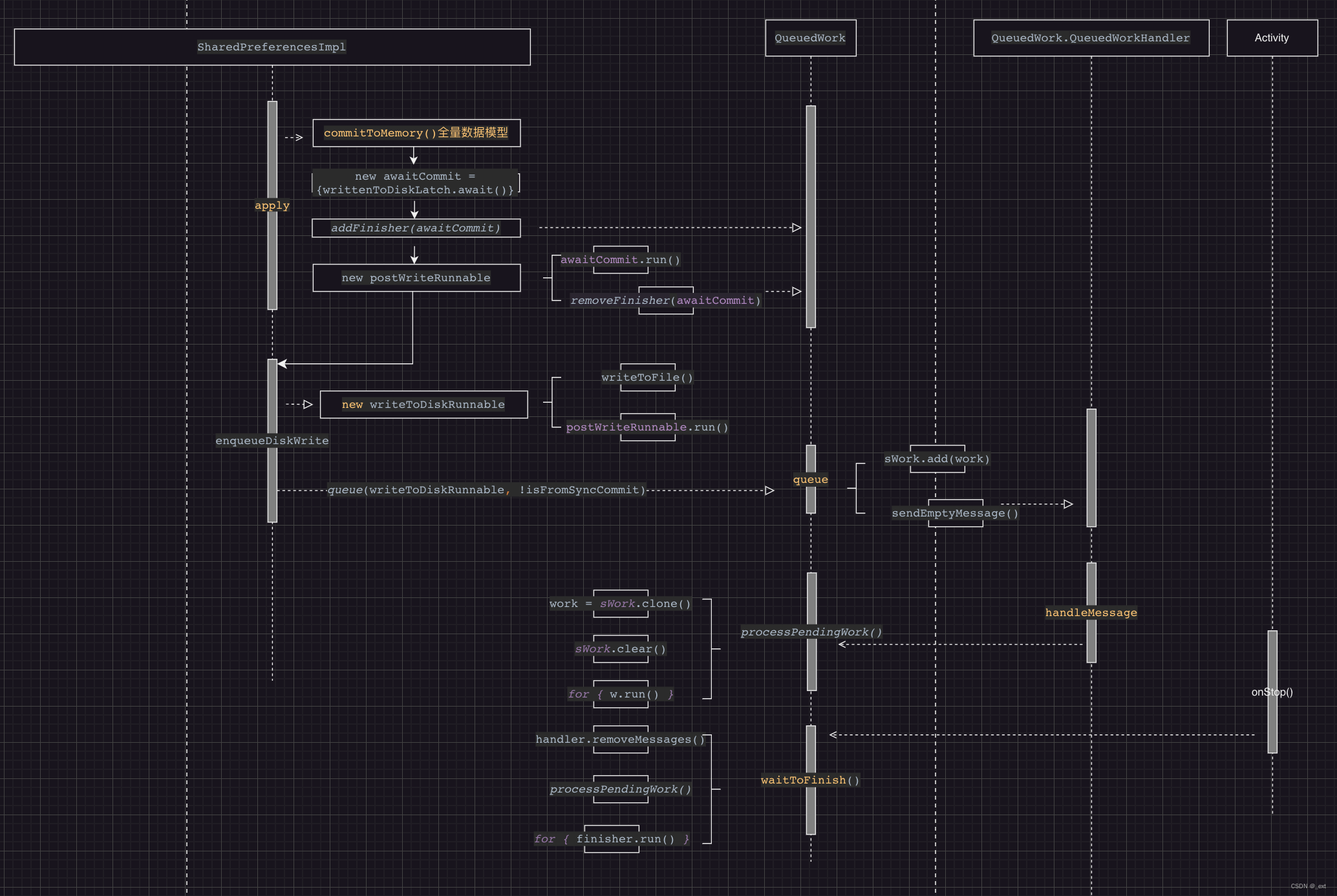
SharedPreferences卡顿分析
SP的使用及存在的问题 SharedPreferences(以下简称SP)是Android本地存储的一种方式,是以key-value的形式存储在/data/data/项目包名/shared_prefs/sp_name.xml里,SP的使用示例及源码解析参见:Android本地存储之SharedPreferences源码解析。以…...
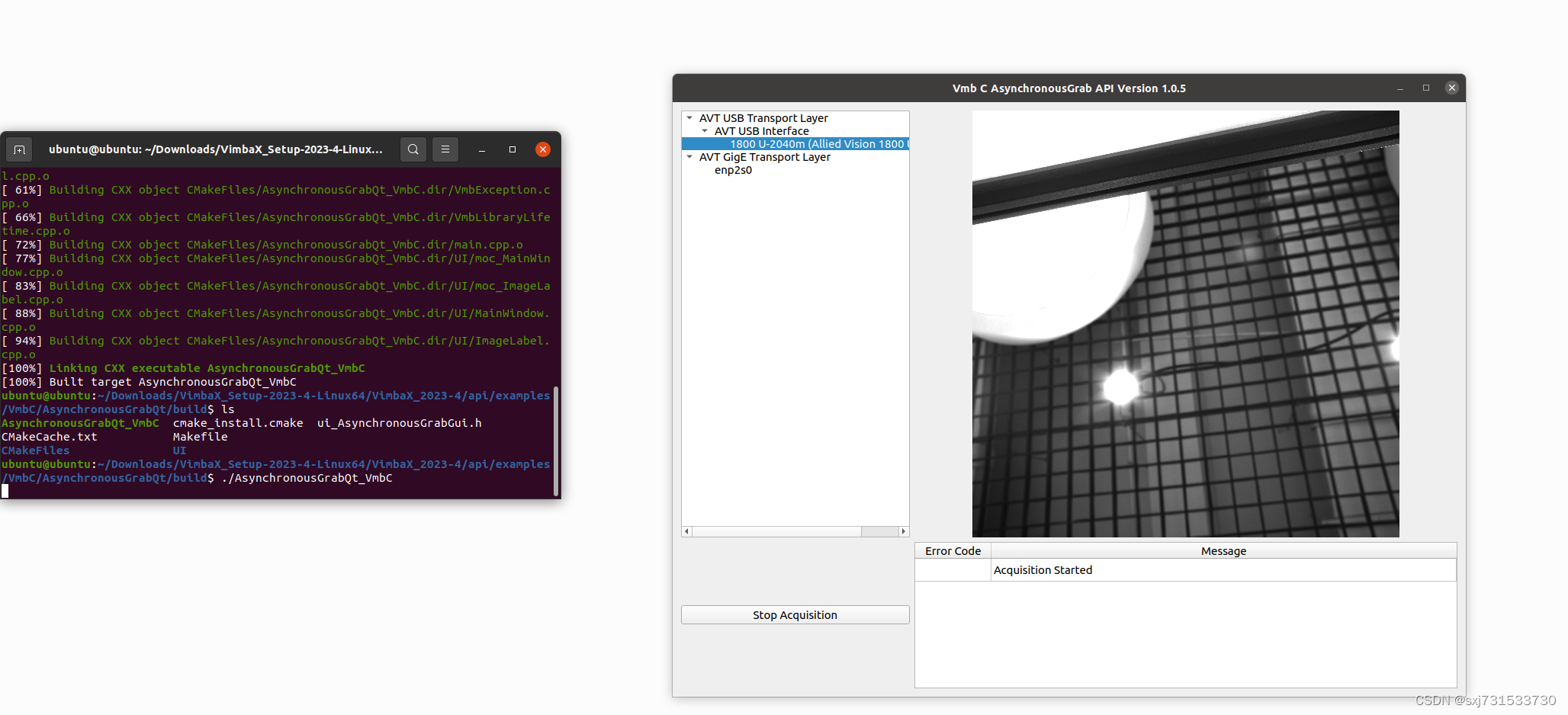
64、ubuntu使用c++/python调用alliedvisio工业相机
基本思想:需要使用linux系统调用alliedvisio工业相机完成业务,这里只做驱动相机调用,具体不涉及业务开发 Alvium 相机选型 - Allied Vision 一、先用软件调用一下用于机器视觉和嵌入式视觉的Vimba X 软件开发包 - Allied Vision VimbaX_Set…...

网络端口与 IP 地址有什么区别?
网络端口和IP地址是计算机网络中两个非常重要的概念,它们在实现网络通信和数据传输中扮演着不同的角色。 IP地址 IP地址(Internet Protocol Address)是用于标识网络上设备的唯一地址。它是一个由数字组成的标识符,用于在网络中准…...

C语言标准的输入输出
目录 1. 格式化输入输出 2. 控制字符串长度 3. 混合格式化输出 4. 格式化浮点数 5. 格式化日期和时间 在C语言编程中,输入输出格式非常重要,它决定了程序如何向用户展示数据以及如何从用户接收数据。本篇博客将介绍C语言输入输出格式的一些基本概念…...

C++ 类与对象(上)
目录 本节目标 1.面向过程和面向对象初步认识 2.类的引入 3.类的定义 4.类的访问限定符及封装 4.1 访问限定符 4.2 封装 5. 类的作用域 6. 类的实例化 7.类对象模型 7.1 如何计算类对象的大小 7.2 类对象的存储方式猜测 7.3 结构体内存对齐规则 8.this指针 8.1 thi…...
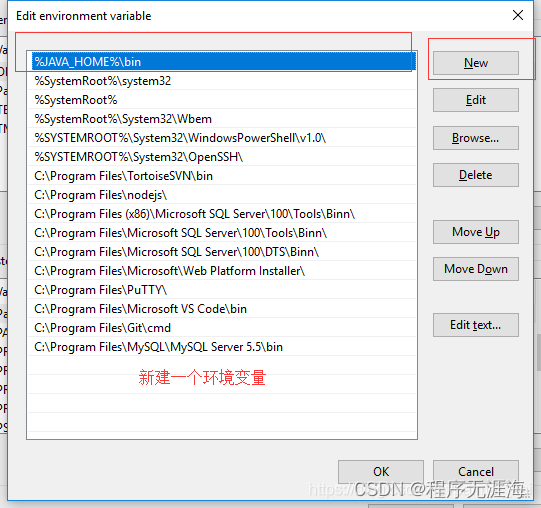
如何配置MacLinuxWindows环境变量
这里写目录标题 什么是环境变量什么是PATH为什么要配置环境变量 如何配置环境变量环境变量有哪些环境变量加载顺序环境变量加载详解 配置参考方法一: export PATHLinux环境变量配置方法二:vim ~/.bashrcLinux环境变量配置方法三:vim ~/.bash_…...
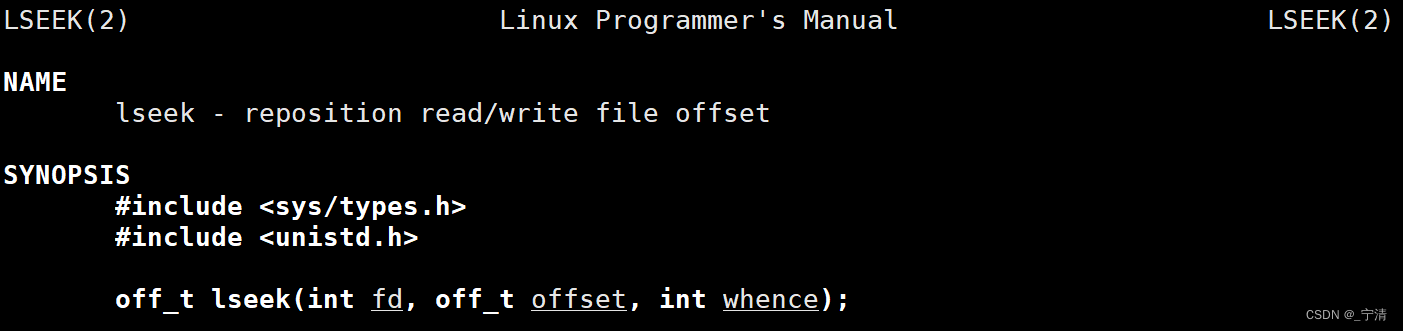
【Linux】从C语言文件操作 到Linux文件IO | 文件系统调用
文章目录 前言一、C语言文件I/O复习文件操作:打开和关闭文件操作:顺序读写文件操作:随机读写stdin、stdout、stderr 二、承上启下三、Linux系统的文件I/O系统调用接口介绍open()close()read()write()lseek() Linux文件相关重点 复习C文件IO相…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
