【C/C++ 01】初级排序算法
排序算法通常是针对数组或链表进行排序,在C语言中,需要手写排序算法完成对数据的排序,排序规则通常为升序或降序(本文默认为升序),在C++中,<algorithm>头文件中已经封装了基于快排算法的 std::sort() 函数,但是快速排序是不稳定的排序算法,于是<algorithm>中还包含了 stable_sort() 函数,即保留了等值元素的相对顺序。
稳定性:通常,在排序算法中,稳定性是指如果两个元素在原始数组中的相对顺序保持不变,则在排序后它们的相对顺序也应该保持不变。换句话说,如果有两个相等的元素,它们的位置在排序之前是 a 和 b,且 a 在 b 的前面,那么在排序后,a 仍然应该在 b 的前面。
在进行排序算法之前,先定义一个用于交换元素位置的函数:
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}一、冒泡排序(Bubble Sort)
冒泡排序的核心算法是暴力求解思维,是指将所有元素都相互比较一次,若靠前的数比靠后的数大,则将两个数交换位置。
- 排序对象:数组
- 时间复杂度:
- 空间复杂度:
- 是否稳定:是
void BubbleSort(int* arr, int n)
{for (int i = 0; i < n; ++i){for (int j = 0; j < n - i - 1; ++j){if (arr[j] > arr[j + 1]){Swap(&arr[j], &arr[j + 1]);}}}
}二、插入排序(Insert Sort)
插入排序的核心算法是将当前遍历到的地方的末尾数据往前比较,找到合适的位置进行插入,直到遍历到最后一个数据。
- 排序对象:数组、链表
- 时间复杂度:
- 空间复杂度:
- 是否稳定:是
void InsertSort(int* arr, int n)
{int i = 1;for (; i < n; ++i){int j = i;int end = arr[j];while (j > 0 && arr[j - 1] > end){arr[j] = arr[j - 1];--j;}arr[j] = end;}
}三、选择排序(Select Sort)
选择排序的算法核心是找到数组的最大值和最小值,将其和遍历数组的左右端进行交换,然后左端右移、右端左移。简易版的选择排序算法会只找一个最值进行交换。
- 排序对象:数组、链表
- 时间复杂度:
- 空间复杂度:
- 是否稳定:否
void SelectSort(int* arr, int n)
{int left = 0;int right = n - 1;while (left < right){int iMin = left; int iMax = right;for (int i = left; i <= right; ++i){if (arr[i] < arr[iMin])iMin = i;if (arr[i] > arr[iMax])iMax = i;} Swap(&arr[left], &arr[iMin]);if (left == iMax)iMax = iMin;Swap(&arr[right], &arr[iMax]);++left;--right;}
}相关文章:
【C/C++ 01】初级排序算法
排序算法通常是针对数组或链表进行排序,在C语言中,需要手写排序算法完成对数据的排序,排序规则通常为升序或降序(本文默认为升序),在C中,<algorithm>头文件中已经封装了基于快排算法的 st…...

Android Settings 显示电池点亮百分比
如题,Android 原生 Settings 里有个 电池电量百分比 的选项,打开后电池电量百分比会显示在状态栏。 基于 Android 13 , 代码在 ./packages/apps/Settings/src/com/android/settings/display/BatteryPercentagePreferenceController.java &am…...
Windows记事本不显示下划线的原因及解决方法
最近使用Windows 记事本敲代码发现一个问题:代码中的下划线无法显示!!!(字体为“微软雅黑”、字体大小为11下,代码中的下划线无法显示。当然每个人情况可能不同) 在 Windows 记事本中,下划线可能会因为 字体…...
(四十六))
嵌入式软件工程师面试题——2025校招社招通用(C/C++)(四十六)
说明: 面试群,群号: 228447240面试题来源于网络书籍,公司题目以及博主原创或修改(题目大部分来源于各种公司);文中很多题目,或许大家直接编译器写完,1分钟就出结果了。但…...
【学网攻】 第(13)节 -- 动态路由(OSPF)
系列文章目录 目录 系列文章目录 文章目录 前言 一、动态路由是什么? 二、实验 1.引入 实验拓扑图 实验配置 实验验证 总结 文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻】 第(2)节 -- 交换机认识及使用【学网攻】 第(3)节 -- 交换机配置聚合端口【学…...

Asp.Net Core 获取应用程序相关目录
在ASP.NET Core中,可以通过以下三种方式获取应用程序所在目录: 1、使用AppContext.BaseDirectory属性: string appDirectory AppContext.BaseDirectory; 例如:D:\后端项目\testCore\test.WebApi\bin\Debug\net6.0\ 2、使用…...
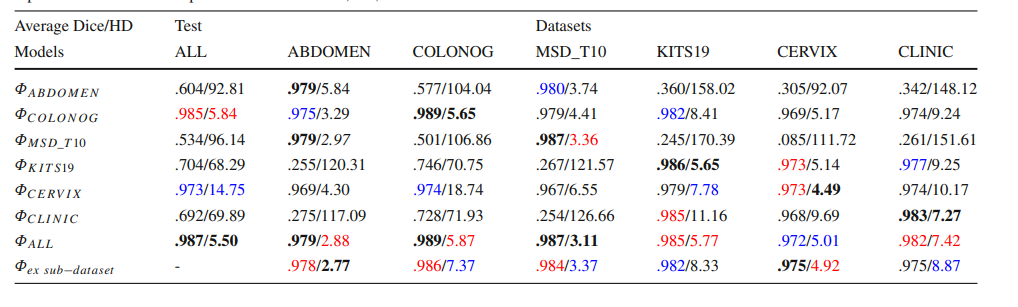
文献速递:人工智能医学影像分割--- 深度学习分割骨盆骨骼:大规模CT数据集和基线模型
文献速递:人工智能医学影像分割— 深度学习分割骨盆骨骼:大规模CT数据集和基线模型 我们为大家带来人工智能技术在医学影像分割上的应用文献。 人工智能在医学影像分析中发挥着至关重要的作用,尤其体现在图像分割技术上。这项技术的目的是准…...
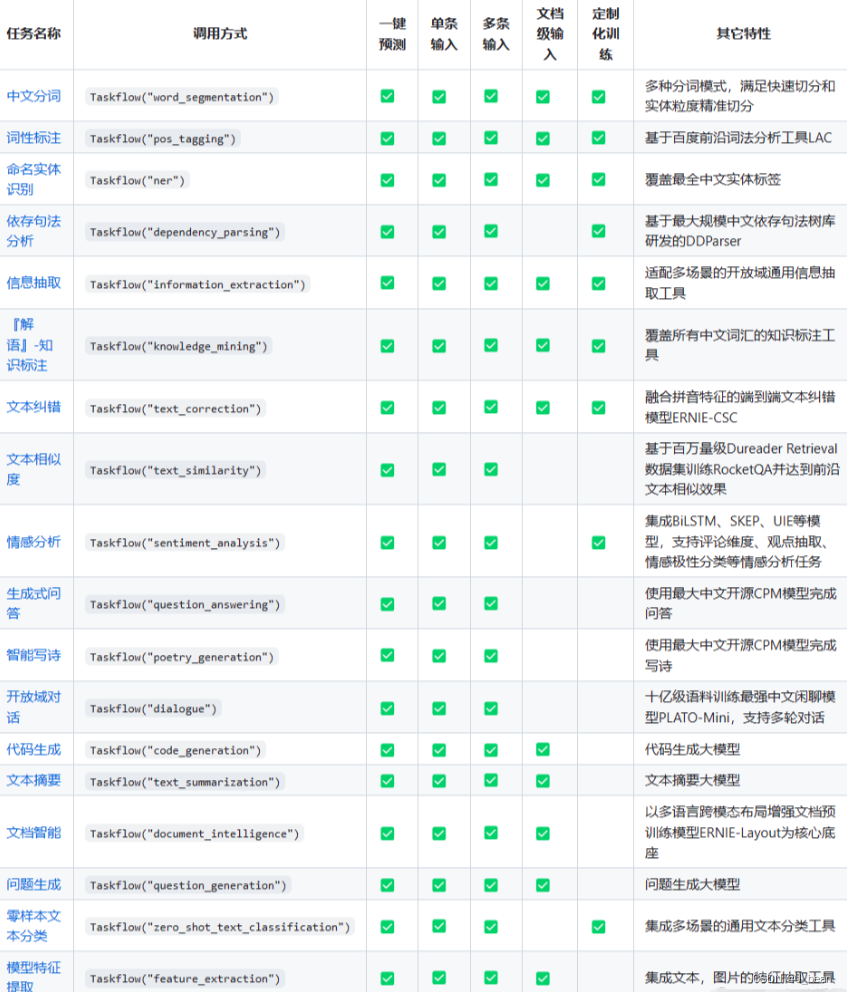
PaddleNLP的简单使用
1 介绍 PaddleNLP是一个基于PaddlePaddle深度学习平台的自然语言处理(NLP)工具库。 它提供了一系列用于文本处理、文本分类、情感分析、文本生成等任务的预训练模型、模型组件和工具函数。 PaddleNLP有统一的应用范式:通过 paddlenlp.Task…...
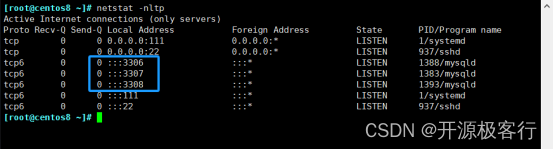
2. MySQL 多实例
重点: MySQL 的 三种安装方式:包安装,二进制安装,源码编译安装。 MySQL 的 基本使用 MySQL 多实例 DDLcreate alter drop DML insert update delete DQL select 2.5)通用 二进制格式安装 MySQL 2.5.1ÿ…...

两个五层决策树和一个十层决策树的区别
随机森林的弹性: 随机森林中的多个决策树是相互独立构建的,因此两个五层决策树和一个十层决策树之间的区别可能在于它们对训练数据的不同学习。这种弹性有助于模型更好地适应不同的数据模式。 过拟合风险: 十层决策树可能更容易过拟合训练数据,尤其是在数…...
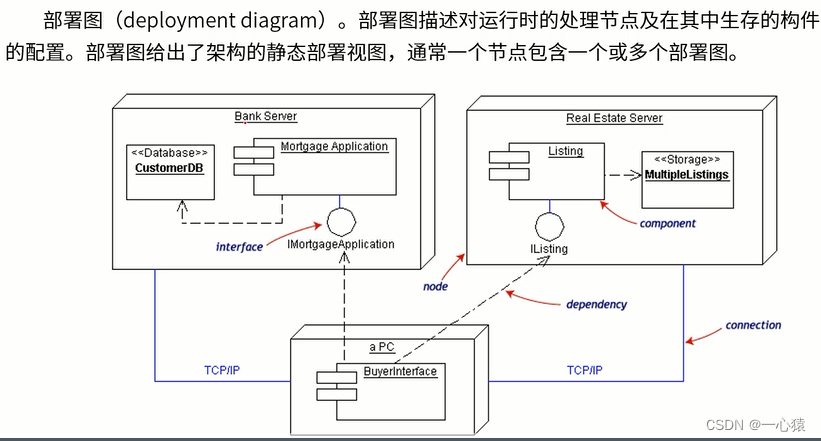
案例分析技巧-软件工程
一、考试情况 需求分析(※※※※)面向对象设计(※※) 二、结构化需求分析 数据流图 数据流图的平衡原则 数据流图的答题技巧 利用数据平衡原则,比如顶层图的输入输出应与0层图一致补充实体 人物角色:客户、…...
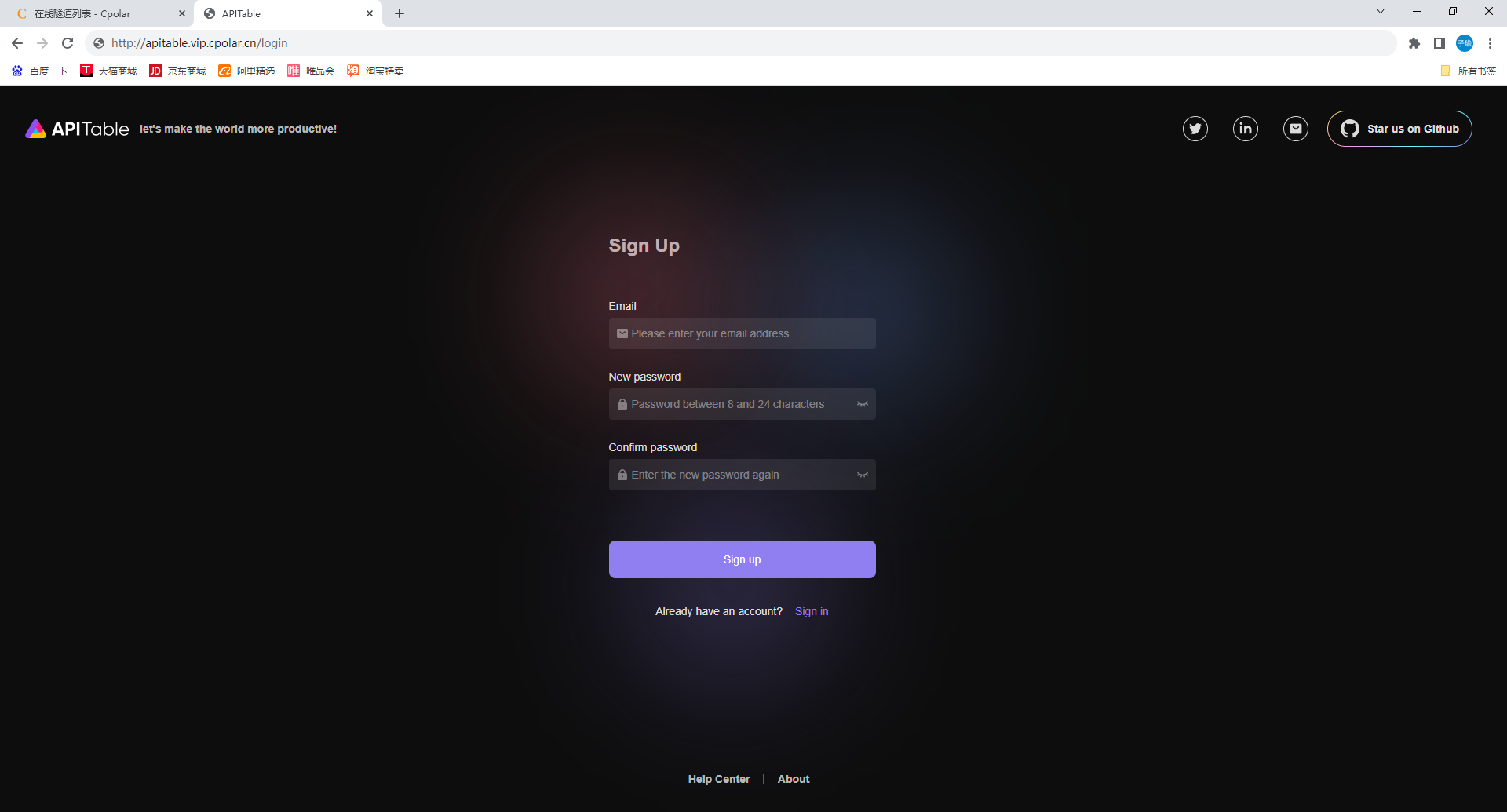
如何使用docker compose安装APITable并远程访问登录界面
文章目录 前言1. 部署APITable2. cpolar的安装和注册3. 配置APITable公网访问地址4. 固定APITable公网地址 正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通俗易懂,风趣幽默,忍不住分享一下给大家。 …...

深入了解Matplotlib中的子图创建方法
深入了解Matplotlib中的子图创建方法 一 add_axes( **kwargs):1.1 函数介绍1.2 示例一 创建第一张子图1.2 示例二 polar参数的运用1.3 示例三 创建多张子图 二 add_subplot(*args, **kwargs):2.1 函数介绍2.2 示例一 三 两种方法的区别3.1 参数形式3.2 布局灵活性3.3 适用场景3…...

云计算运维 · 第三阶段 · git
学习b记 第三阶段 三、持续集成 1、git #安装 yum -y install git[rootgit-git ~]# git config –-global user.name "qxl" # 配置git使用用户 [rootgit-git ~]# git config –-global user.email "qxlmail.com" # 配置git使用邮箱 [rootgit-git ~]# g…...

【幻兽帕鲁】开服务器,高性能高带宽(100mbps),免费!!!【学生党强推】
【幻兽帕鲁】开服务器,高性能高带宽(100mbps),免费!!!【学生党强推】 教程相关视频地址:https://www.bilibili.com/video/BV16e411Y7Fd/ 目前幻兽帕鲁开服务器有以下几套比较性价比的…...
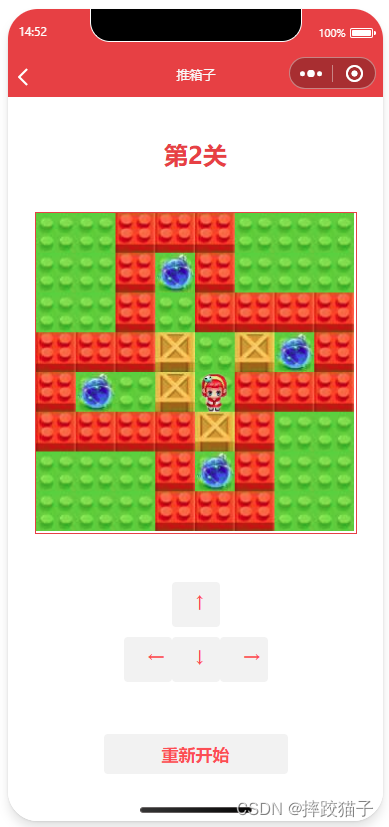
微信小程序|推箱子小游戏
推箱子游戏是一种经典的益智游戏,通过移动箱子将其推到指定位置,完成关卡的过程。随着小程序的发展,越来越多的人开始在手机上玩推箱子游戏。本文将介绍如何利用小程序实现推箱子游戏,并分享一些技术实现的方法。 目录 引言游戏背景介绍游戏规则及挑战技术实现步骤创建游戏…...

【Linux】—— 信号的产生
本期,我们今天要将的是信号的第二个知识,即信号的产生。 目录 (一)通过终端按键产生信号 (二)调用系统函数向进程发信号 (三)由软件条件产生信号 (四)硬件…...

【算法】Hash 算法-关注优化细节
//给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 // // 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 // // // // 示例 1: // // //输入:nums [100,4…...
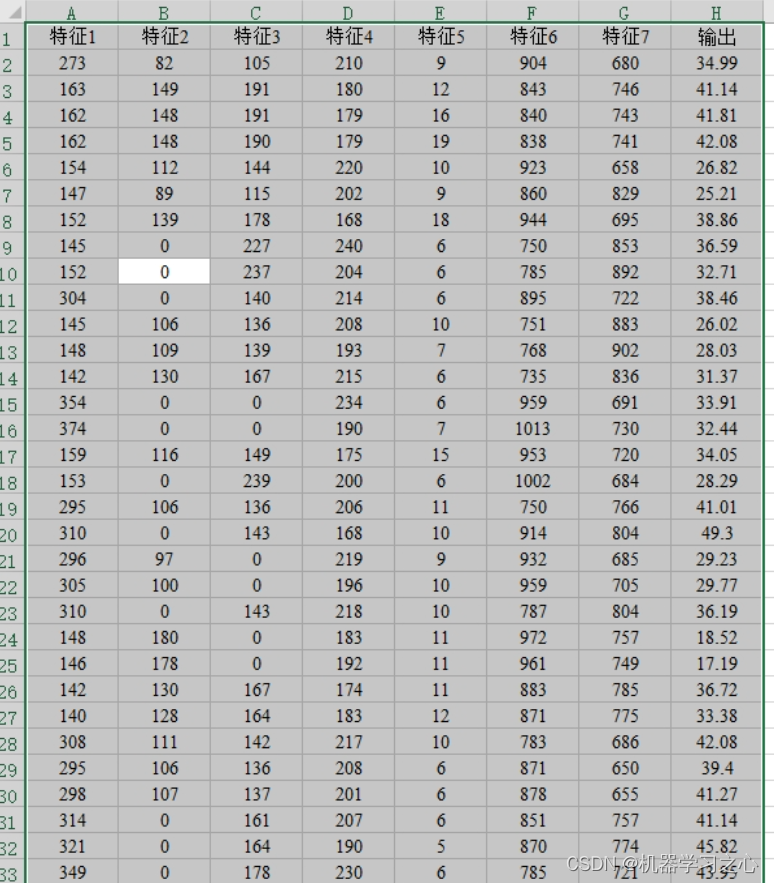
回归预测 | Matlab实现CPO-SVR冠豪猪优化支持向量机的数据多输入单输出回归预测
回归预测 | Matlab实现CPO-SVR冠豪猪优化支持向量机的数据多输入单输出回归预测 目录 回归预测 | Matlab实现CPO-SVR冠豪猪优化支持向量机的数据多输入单输出回归预测预测效果基本描述程序设计参考资料 预测效果 基本描述 1.Matlab实现CPO-SVR冠豪猪优化支持向量机的数据多输入…...
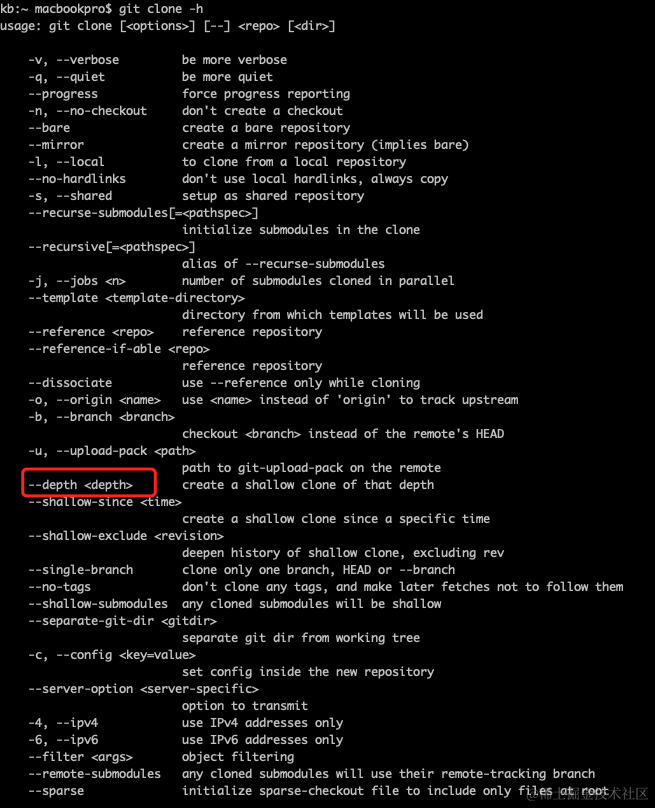
Idea设置代理后无法clone git项目
背景 对于我们程序员来说,经常上github找项目、找资料是必不可少的,但是一些原因,我们访问的时候速度特别的慢,需要有个代理,才能正常的访问。 今天碰到个问题,使用idea工具 clone项目,速度特…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
