代码随想录算法训练营第17天(二叉树5)| 找树左下角的值二叉树的路径总和从中序与后序遍历序列构造二叉树从前序与中序遍历序列构造二叉树
513.找树左下角的值
leetcode题目地址
题目链接/文章讲解/视频讲解
如果使用递归法,如何判断是最后一行:
其实就是深度最大的叶子节点一定是最后一行。
//迭代法
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);int result = 0;while (!que.empty()) {int size = que.size();for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (i == 0) result = node->val; // 记录最后一行第一个元素if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return result;}
};//递归法
class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* root, int depth) {if (root->left == NULL && root->right == NULL) {if (depth > maxDepth) {maxDepth = depth;result = root->val;}return;}if (root->left) {traversal(root->left, depth + 1); // 隐藏着回溯,下一个遍历的时候深度加一,本层的不变}if (root->right) {traversal(root->right, depth + 1); // 隐藏着回溯, 下一个遍历的时候深度加一,本层的不变}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};112. 路径总和
leetcodet题目链接
题目链接/文章讲解/视频讲解
因为终止条件是判断叶子节点,所以递归的过程中就不要让空节点进入递归了。
递归函数是有返回值的,如果递归函数返回true,说明找到了合适的路径,应该立刻返回。
左右子树递归时候的返回值要做判断,如果有一支返回true就可以提前返回结果,如果都没有返回true,返回false
class Solution {
private:bool traversal(TreeNode* cur, int count) {if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点,并且计数为0if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回if (cur->left) { // 左count -= cur->left->val; // 递归,处理节点;if (traversal(cur->left, count)) return true;// 提前结束递归count += cur->left->val; // 回溯,撤销处理结果}if (cur->right) { // 右count -= cur->right->val; // 递归,处理节点;if (traversal(cur->right, count)) return true;// 提前结束递归count += cur->right->val; // 回溯,撤销处理结果}return false;}public:bool hasPathSum(TreeNode* root, int sum) {if (root == NULL) return false;return traversal(root, sum - root->val);}
};
106.从中序与后序遍历序列构造二叉树
106.从中序与后序遍历序列构造二叉树,105.从前序与中序遍历序列构造二叉树
leetcode题目链接
题目链接/文章讲解/视频讲解
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
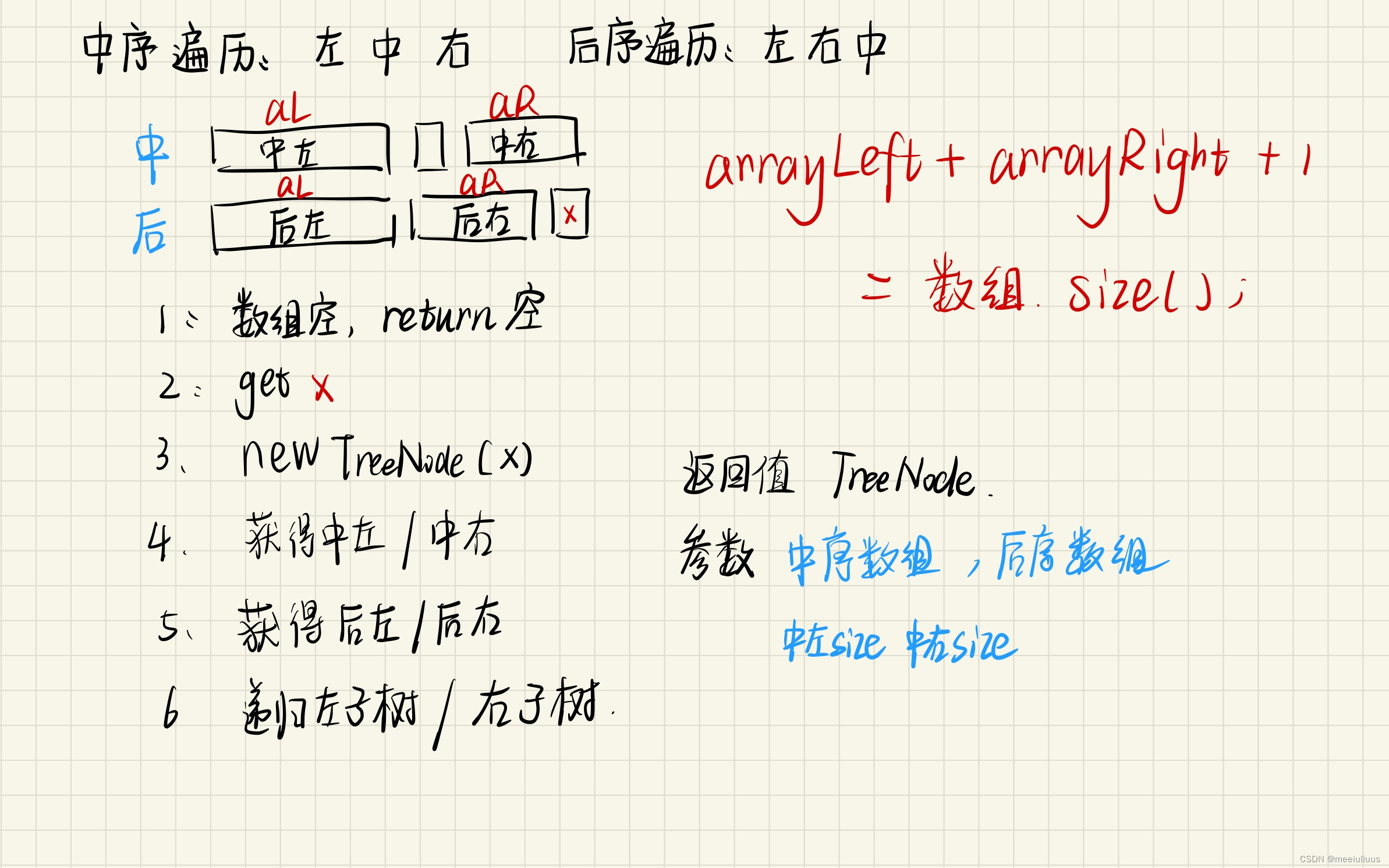
第一步:如果数组大小为零的话,说明是空节点了。
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
第五步:切割后序数组,切成后序左数组和后序右数组
第六步:递归处理左区间和右区间
//框架代码
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {// 第一步if (postorder.size() == 0) return NULL;// 第二步:后序遍历数组最后一个元素,就是当前的中间节点int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);// 叶子节点if (postorder.size() == 1) return root;// 第三步:找切割点int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 第四步:切割中序数组,得到 中序左数组和中序右数组// 第五步:切割后序数组,得到 后序左数组和后序右数组// 第六步root->left = traversal(中序左数组, 后序左数组);root->right = traversal(中序右数组, 后序右数组);return root;
}//完整代码
class Solution {
private:TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {if (postorder.size() == 0) return NULL;// 后序遍历数组最后一个元素,就是当前的中间节点int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);// 叶子节点if (postorder.size() == 1) return root;// 找到中序遍历的切割点int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组// 左闭右开区间:[0, delimiterIndex)vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);// [delimiterIndex + 1, end)vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );// postorder 舍弃末尾元素postorder.resize(postorder.size() - 1);// 切割后序数组// 依然左闭右开,注意这里使用了左中序数组大小作为切割点// [0, leftInorder.size)vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());// [leftInorder.size(), end)vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());root->left = traversal(leftInorder, leftPostorder);root->right = traversal(rightInorder, rightPostorder);return root;}
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (inorder.size() == 0 || postorder.size() == 0) return NULL;return traversal(inorder, postorder);}
};相关文章:
| 找树左下角的值二叉树的路径总和从中序与后序遍历序列构造二叉树从前序与中序遍历序列构造二叉树)
代码随想录算法训练营第17天(二叉树5)| 找树左下角的值二叉树的路径总和从中序与后序遍历序列构造二叉树从前序与中序遍历序列构造二叉树
513.找树左下角的值 leetcode题目地址 题目链接/文章讲解/视频讲解 如果使用递归法,如何判断是最后一行: 其实就是深度最大的叶子节点一定是最后一行。 //迭代法 class Solution { public:int findBottomLeftValue(TreeNode* root) {queue<TreeNod…...
代码随想录 Leetcode106. 从中序与后序遍历序列构造二叉树
题目: 代码(首刷看解析 2024年1月30日): class Solution { public:TreeNode* recursion(vector<int>& inorder, vector<int>& postorder, int longthOfLeft, int longthOfRight) {if (postorder.size() 0) …...

Log4j Log4j2
前言 今天抽时间来把这个日志框架学学,毕竟经常用,虽然不用自己写,但是书到用时方恨少,技多不压身。而且最近我的 GUI 软件中有一个关于日志问题的希望学完能够感觉解决掉。 Log4j & Log4j2 Log4j2 是 Log4j 的升级版&#x…...
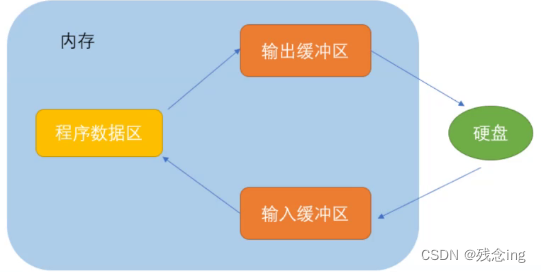
C语言——如何进行文件操作
大家好,我是残念,希望在你看完之后,能对你有所帮助,有什么不足请指正!共同学习交流 本文由:残念ing原创CSDN首发,如需要转载请通知 个人主页:残念ing-CSDN博客,欢迎各位→…...

python中for循环的几个现象
1. 运行如下代码 l [{}, {}, {}] for k in l:k[1] 1 print(l) 输出为 [{1: 1}, {1: 1}, {1: 1}]2. 运行如下代码 l [{}, {}, {}] for k in l:k {1:1} print(l) 输出为 [{}, {}, {}] 3. 运行如下代码 l [1,2,3] for k in l:k k * 2 print(l)输出为 [1, 2, 3…...
openssl3.2 - 测试程序的学习 - 准备openssl测试专用工程的模板
文章目录 openssl3.2 - 测试程序的学习 - 准备openssl测试专用工程的模板概述笔记工程中需要的openssl的库实现补充 - 最终的模板工程END openssl3.2 - 测试程序的学习 - 准备openssl测试专用工程的模板 概述 openssl3.2 - 测试程序的学习 整了几个test.c, 每开一个新的测试工…...

Delphi.cz采访Embarcadero捷克共和国办事处经理:理查德·库巴特 - 第一部分
Embarcadero捷克办事处主任理查德库巴特(Richard Kubt,55 岁)接受了我的采访。 Radek Červinka (RČ):库巴特先生您好,感谢您抽出时间访问 delphi.cz。 一开始:我在某处听说您是一名程序员,从…...
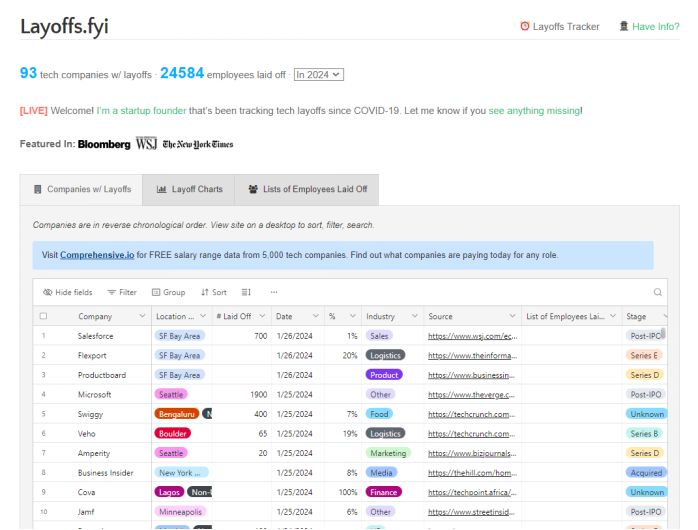
AI投资或成科技裁员罪魁祸首
最近的科技裁员让许多人对这个行业的稳定性产生了疑问。然而,仔细观察发现,这些裁员并不是经济困境的迹象,而是科技公司为了重新调整优先事项并投资未来而进行的战略举措。科技行业正投入数十亿美元用于人工智能(AI)&a…...
解读BEVFormer,新一代自动驾驶视觉工作的基石
文章出处 BEVFormer这篇文章很有划时代的意义,改变了许多视觉领域工作的pipeline[2203.17270] BEVFormer: Learning Birds-Eye-View Representation from Multi-Camera Images via Spatiotemporal Transformers (arxiv.org)https://arxiv.org/abs/2203.17270 BEV …...

【React教程】(1) React简介、React核心概念、React初始化
目录 ReactReact 介绍React 特点React 的发展历史React 与 Vue 的对比技术层面开发团队社区Native APP 开发 相关资源链接 EcmaScript 6 补充React 核心概念组件化虚拟 DOM 起步初始化及安装依赖Hello World React React 介绍 React 是一个用于构建用户界面的渐进式 JavaScrip…...

云计算中的弹性是什么?
云弹性是指当客户需求增加或减少时,自动从数据中心配置和取消配置资源。这使得云资源(包括计算、存储和内存资源)能够根据需求变化快速重新分配。CPU/处理、内存、输入/输出带宽和存储容量等计算资源可以根据需要增加或减少,而不会影响系统性能。 它旨在…...

Vue3基础:pnpm是什么?npm和pnpm的区别?如何使用pnpm?
pnpm 是一个流行的 JavaScript 包管理器,类似于 npm 和 yarn。它是 performant npm 的缩写,意在表明它是一个更高效的 npm 替代品。pnpm 的主要特点和优势包括: 高效的存储空间使用 pnpm 使用称为“内容寻址存储”的机制来存储 npm 包。这意…...
)
vue中父组件直接调用子组件方法(通过ref)
目录 1、vue2 中,父组件调用子组件的方法 2、vue3 中,父组件调用子组件的方法 1、vue2 中,父组件调用子组件的方法 在Vue 2中,父组件可以通过使用ref属性来引用子组件的实例,然后通过该实例调用子组件的方法。 首先…...
Gunicorn性能优化:提升Python Web应用的服务效率
在Python Web开发中,Gunicorn作为WSGI HTTP服务器,常常作为Web应用(如Django或Flask)与反向代理或负载均衡器之间的桥梁。为了充分发挥其性能,本文将提供一些实用的Gunicorn配置建议。 Gunicorn架构 Gunicorn采用了预…...

如何使用ssh key免密码登录服务器?
以下是使用密钥对免密码登录服务器的具体指令操作步骤: 步骤一:生成密钥对 在本地电脑上打开终端或命令提示符,运行以下命令生成密钥对: ssh-keygen -t rsa -C "your_emailexample.com" 该命令会提示您选择保存密钥…...
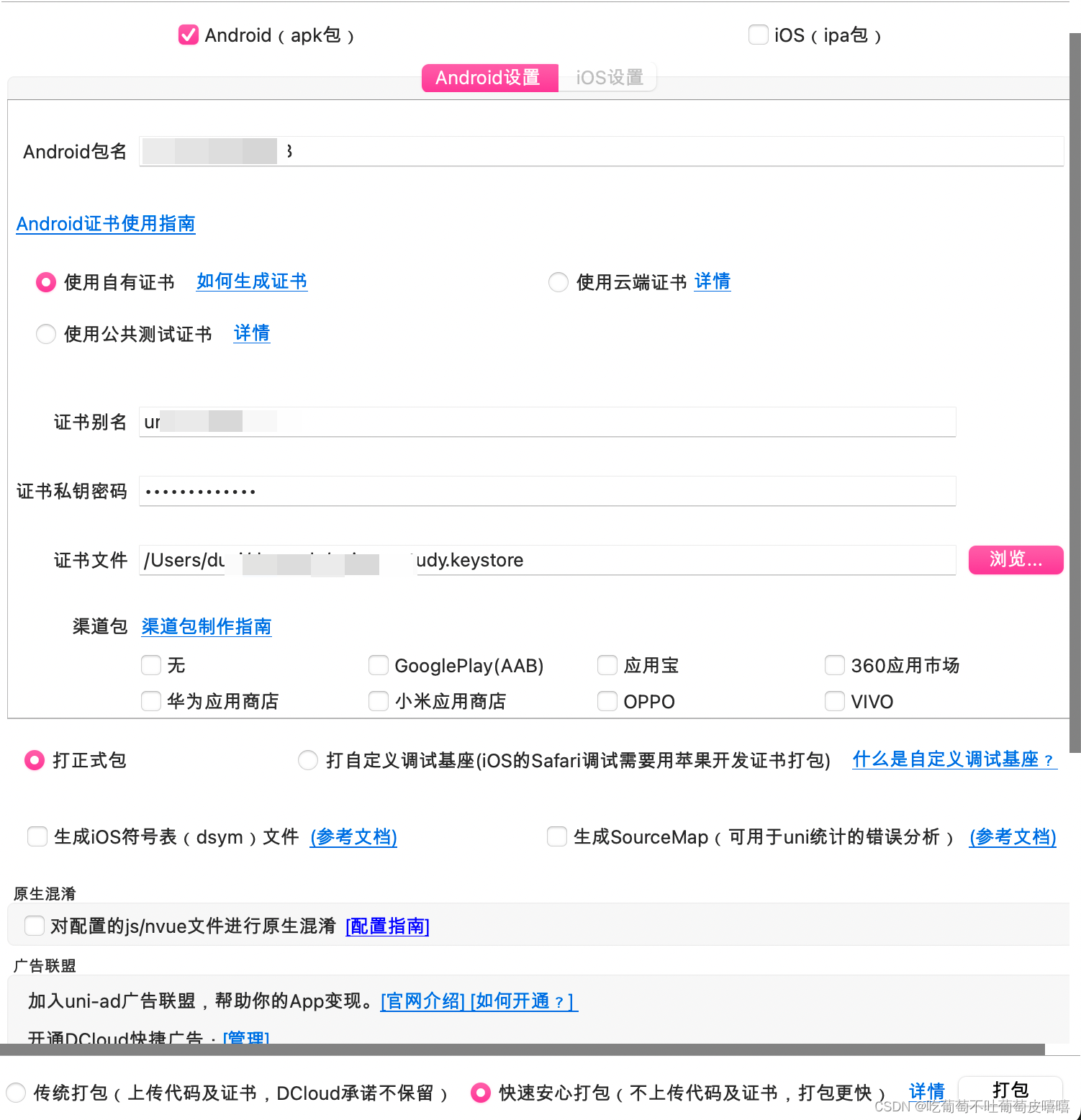
macos Android平台签名证书(.keystore)
一、申请appid的使用说明(有appid的请忽略申请appid) 创建应用 申请的appid在源码视图填写后会自动生成一个对应的包名 ⚠️注意:申请appid的时候应用名称和项目名称保持一致。 二、 Android如何使用自用证书进行打包 1.找到安装jdk的路径…...
Kotlin快速入门系列2
Kotlin的基本数据类型 Kotlin 的基本数值类型包括 Byte、Short、Int、Long、Float、Double 等。不同于 Java 的是,字符不属于数值类型,是一个独立的数据类型。 Java和kotlin数据类型对照如下: Java基本数据类型 Kotlin对象数据类型 数据类…...
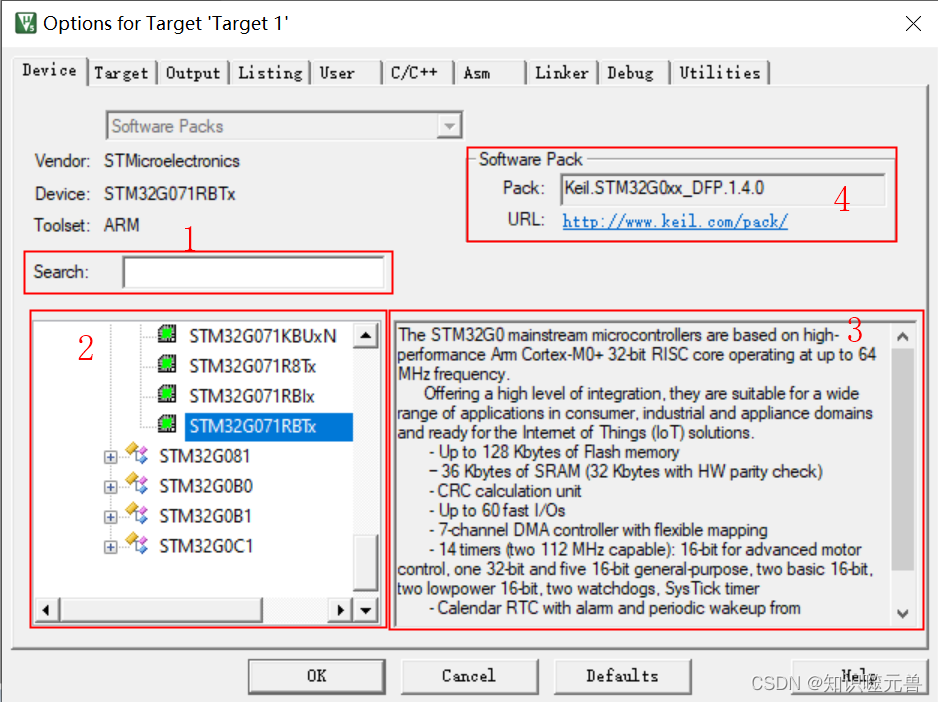
单片机之keil软件环境搭建
简介 Keil提供了包括C编译器、宏汇编、链接器、库管理和一个功能强大的仿真调试器等在内的完整开发方案,通过一个集成开发环境(μVision)将这些部分组合在一起。 目前软件对中文的支持不友好,不建议安装网上的一些汉化包…...
数学公式OCR识别php 对接mathpix api 使用公式编译器
数学公式OCR识别php 对接mathpix api 一、注册账号官网网址:https://mathpix.com 二、该产品支持多端使用注意说明(每月10次) 三、api 对接第一步创建create keyphp对接api这里先封装两个请求函数,get 和post ,通过官方…...
MySQL原理(二)存储引擎(1)概述
一、存储引擎介绍 1、概念: (1)MySQL中的数据用各种不下同的技术存储在文件中,每一种技术都使用不同的存储机制、索引技巧、锁定水平并最终提供不同的功能和能力,这些不同的技术以及配套的功能在MySQL中称为存储引擎…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
