深度强化学习(王树森)笔记09
深度强化学习(DRL)
本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。
参考链接
Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL
源代码链接:https://github.com/DeepRLChinese/DeepRL-Chinese
B站视频:【王树森】深度强化学习(DRL)
豆瓣: 深度强化学习
文章目录
- 深度强化学习(DRL)
- 带基线的策略梯度方法
- 策略梯度中的基线
- 基线 (Baseline)
- 基线的直观解释
- 带基线的 REINFORCE 算法
- 策略网络和价值网络
- 算法的推导
- 训练流程
- Advantage Actor-Critic (A2C)
- 算法推导
- 训练流程
- 用目标网络改进训练
- 总结
- 后记
带baseline的策略梯度方法:REINFORCE with baseline和advantage actor-critic (A2C)
带基线的策略梯度方法
上一章推导出策略梯度,并介绍了两种策略梯度方法——REINFORCE 和 actor-critic。
虽然上一章的方法在理论上是正确的,但是在实践中效果并不理想。本章介绍的带基线的策略梯度 (policy gradient with baseline) 可以大幅提升策略梯度方法的表现。使用基线(baseline) 之后,REINFORCE 变成 REINFORCE with baseline, actor-critic 变成 advantage actor-critic (A2C)。
策略梯度中的基线
首先回顾上一章的内容。策略学习通过最大化目标函数 J ( θ ) = E S [ V π ( S ) ] J(\theta)=\mathbb{E}_S[V_\pi(S)] J(θ)=ES[Vπ(S)], 训练出策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ)。可以用策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ) 来更新参数 θ \theta θ:
θ n e w ← θ n o w + β ⋅ ∇ θ J ( θ n o w ) . \theta_{\mathrm{new}}\:\leftarrow\:\theta_{\mathrm{now}}+\beta\cdot\nabla_{\theta}\:J(\boldsymbol{\theta_{now}}). θnew←θnow+β⋅∇θJ(θnow).
策略梯度定理证明:
∇ θ J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S , θ ) [ Q π ( S , A ) ⋅ ∇ θ ln π ( A ∣ S ; θ ) ] ] . ( 8.1 ) \boxed{\quad\nabla_\theta J(\boldsymbol{\theta})~=~\mathbb{E}_S\biggl[\mathbb{E}_{A\sim\pi(\cdot|S,\boldsymbol{\theta})}\biggl[\:Q_\pi(S,A)~\cdot~\nabla_\theta\:\ln\pi(A\mid S;\boldsymbol{\theta})\biggr]\biggr].} \quad{(8.1)} ∇θJ(θ) = ES[EA∼π(⋅∣S,θ)[Qπ(S,A) ⋅ ∇θlnπ(A∣S;θ)]].(8.1)
上一章中,我们对策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ) 做近似,推导出 REINFORCE 和 actor-critic; 两种方法区别在于具体如何做近似。
基线 (Baseline)
基于策略梯度公式 (8.1) 得出的 REINFORCE 和 actor-critic 方法效果通常不好。只需对策略梯度公式 (8.1) 做一个微小的改动,就能大幅提升表现:把 b b b 作为动作价值函数 Q π ( S , A ) Q_{\pi}(S,A) Qπ(S,A) 的基线 (baseline), 用 Q π ( S , A ) − b Q_{\pi}(S,A)-b Qπ(S,A)−b 替换掉 Q π Q_{\pi} Qπ。设 b b b 是任意的函数,只要不依赖于动作 A A A 就可以,例如 b b b 可以是状态价值函数 V π ( S ) V_\pi(S) Vπ(S) 。
定理 8.1. 带基线的策略梯度定理
设 b b b 是任意的函数,但是 b b b 不能依赖于 A A A。把 b b b 作为动作价值函数 Q π ( S , A ) Q_\pi(S,A) Qπ(S,A) 的基线,对策略梯度没有影响:
∇ θ J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ ( Q π ( S , A ) − b ) ⋅ ∇ θ ln π ( A ∣ S ; θ ) ] ] \nabla_{\theta}\:J(\boldsymbol{\theta})\:=\:\mathbb{E}_{S}\bigg[\mathbb{E}_{A\sim\pi(\cdot|S;\boldsymbol{\theta})}\bigg[\bigg(\:Q_{\pi}(S,A)\:-\:{b}\bigg)\:\cdot\:\nabla_{\boldsymbol{\theta}}\:\ln\pi(A|S;\boldsymbol{\theta})\bigg]\bigg]\bigg. ∇θJ(θ)=ES[EA∼π(⋅∣S;θ)[(Qπ(S,A)−b)⋅∇θlnπ(A∣S;θ)]]

定理 8.1 说明 b b b 的取值不影响策略梯度的正确性。不论是让 b = 0 b=0 b=0 还是让 b = V π ( S ) b=V_\pi(S) b=Vπ(S) , 对期望的结果毫无影响,期望的结果都会等于 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ)。其原因在于
E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ b ⋅ ∇ θ ln π ( A ∣ S ; θ ) ] ] = 0. \mathbb{E}_{S}\Big[\mathbb{E}_{A\sim\pi(\cdot|S;\boldsymbol{\theta})}\Big[b\:\cdot\:\nabla_{\boldsymbol{\theta}}\:\ln\pi\big(A|S;\:\boldsymbol{\theta}\big)\Big]\Big]\:=\:0. ES[EA∼π(⋅∣S;θ)[b⋅∇θlnπ(A∣S;θ)]]=0.
定理中的策略梯度表示成了期望的形式,我们对期望做蒙特卡洛近似。从环境中观测到一个状态 s s s,然后根据策略网络抽样得到 a ∼ π ( ⋅ ∣ s ; θ ) a\sim\pi(\cdot|s;\boldsymbol{\theta}) a∼π(⋅∣s;θ)。那么策略梯度 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ) 可以近似为下面的随机梯度:
g b ( s , a ; θ ) = [ Q π ( s , a ) − b ] ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boxed{\quad\boldsymbol{g}_b(s,a;\boldsymbol{\theta})=\left[Q_\pi(s,a)-b\right]\cdot\nabla_\theta\ln\pi(a|s;\boldsymbol{\theta}).} gb(s,a;θ)=[Qπ(s,a)−b]⋅∇θlnπ(a∣s;θ).
不论 b b b 的取值是 0 还是 V π ( s ) V_\pi(s) Vπ(s), 得到的随机梯度 g b ( s , a ; θ ) g_b(s,a;\boldsymbol{\theta}) gb(s,a;θ) 都是 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta}) ∇θJ(θ) 的无偏估计:
Bias = E S , A [ g b ( S , A ; θ ) ] − ∇ θ J ( θ ) = 0. \begin{array}{rcl}{\text{Bias}}&{=}&{\mathbb{E}_{S,A}\left[\boldsymbol{g}_{b}(S,A;\boldsymbol{\theta})\right]\:-\:\nabla_{\theta}J(\boldsymbol{\theta})\:=\:\mathbf{0}.}\\\end{array} Bias=ES,A[gb(S,A;θ)]−∇θJ(θ)=0.
虽然 b b b 的取值对 E S , A [ g b ( S , A ; θ ) ] \mathbb{E}_{S,A}[\boldsymbol{g}_b(S,A;\boldsymbol{\theta})] ES,A[gb(S,A;θ)] 毫无影响,但是 b b b 对随机梯度 g b ( s , a ; θ ) g_b(s,a;\theta) gb(s,a;θ) 是有影响的。用不同的 b b b, 得到的方差
Var = E S , A [ ∥ g b ( S , A ; θ ) − ∇ θ J ( θ ) ∥ 2 ] \text{Var}\:=\:\mathbb{E}_{S,A}\left[\left\|g_{b}(S,A;\:\theta)\:-\:\nabla_{\theta}J(\boldsymbol{\theta})\right\|^{2}\right] Var=ES,A[∥gb(S,A;θ)−∇θJ(θ)∥2]
会有所不同。如果 b b b 很接近 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a) 关于 a a a 的均值,那么方差会比较小。因此, b = V π ( s ) b=V_\pi(s) b=Vπ(s) 是很好的基线。
基线的直观解释
策略梯度公式 (8.1) 期望中的 Q π ( S , A ) ⋅ ∇ θ ln π ( A ∣ S ; θ ) Q_\pi(S,A)\cdot\nabla_\theta\ln\pi(A|S;\boldsymbol{\theta}) Qπ(S,A)⋅∇θlnπ(A∣S;θ) 的意义是什么呢?以图 8.1中的左图为例。
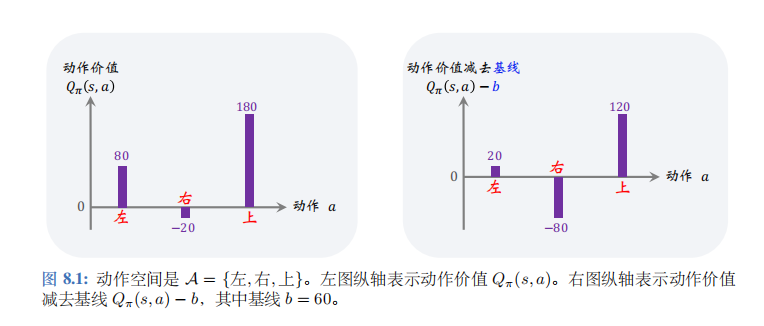
给定状态 s t s_t st, 动作空间是 A = { 左,右,上 } A= \{ 左,右,上\} A={左,右,上}, 动作价值函数给每个动作打分:
Q π ( s t , 左 ) = 80 , Q π ( s t , 右 ) = − 20 , Q π ( s t , 上 ) = 180 , Q_{\pi}(s_{t},\text{左})\:=\:80,\quad Q_{\pi}(s_{t},\text{右})\:=\:-20,\quad Q_{\pi}(s_{t},\text{上})\:=\:180, Qπ(st,左)=80,Qπ(st,右)=−20,Qπ(st,上)=180,
这些分值会乘到梯度 ∇ θ ln π ( A ∣ S ; θ ) \nabla_{\boldsymbol{\theta}}\ln\pi(A|S;\boldsymbol{\theta}) ∇θlnπ(A∣S;θ) 上。在做完梯度上升之后,新的策略会倾向于分值高的动作。
-
动作价值 Q π ( s t , 上 ) = 180 Q_\pi(s_t,上)=180 Qπ(st,上)=180 很大,说明基于状态 s t s_t st 选择动作“上”是很好的决策。让梯度 ∇ θ ln π ( 上 ∣ s t ; θ ) \nabla_{\theta}\ln\pi(上|s_t;\theta) ∇θlnπ(上∣st;θ) 乘以大的系数 Q π ( s t , 上 ) = 180 Q_{\pi}(s_{t}, 上)=180 Qπ(st,上)=180, 那么做梯度上升更新 θ \theta θ 之后,会让 π ( 上 ∣ s t ; θ ) \pi(上|s_t;\theta) π(上∣st;θ) 变大,在状态 s t s_t st 的情况下更倾向于动作“上”。
-
相反, Q π ( s t , 右 ) = − 20 Q_\pi( s_t, 右) = - 20 Qπ(st,右)=−20 说明基于状态 s t s_t st 选择动作“右”是糟糕的决策。让梯度 ∇ θ ln π ( 右 ∣ s t ; θ ) \nabla_{\boldsymbol{\theta}}\ln \pi(右|s_t; \boldsymbol\theta) ∇θlnπ(右∣st;θ) 乘以负的系数 Q π ( s t , 右 ) = − 20 Q_\pi( s_t, 右) = - 20 Qπ(st,右)=−20,那么做梯度上升更新 θ \theta θ 之后, 会让 π ( 右 ∣ s t ; θ ) \pi(右|s_t; \boldsymbol\theta) π(右∣st;θ) 变小,在状态 s t s_t st的情况下选择动作“右”的概率更小。
根据上述分析,我们在乎的是动作价值 Q π ( s t , 左 ) Q_\pi( s_t, 左) Qπ(st,左)、 Q π ( s t , 右 ) Q_\pi( s_t, 右) Qπ(st,右)、 Q π ( s t , 上 ) Q_\pi(s_t,上) Qπ(st,上) 三者的相对大小,而非绝对大小。如果给三者都减去 b = 60 b=60 b=60,那么三者的相对大小是不变的;动作“上”仍然是最好的,动作“右”仍然是最差的。见图 8.1 中的右图。因此
[ Q π ( s t , a t ) − b ] ⋅ ∇ θ ln π ( A ∣ S ; θ ) \begin{bmatrix}Q_\pi(s_t,a_t)-b\end{bmatrix}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(A\:|\:S;\:\boldsymbol{\theta}) [Qπ(st,at)−b]⋅∇θlnπ(A∣S;θ)
依然能指导 θ \theta θ做调整,使得 π ( 上 ∣ s t ; θ ) \pi(上|s_t;\theta) π(上∣st;θ)变大,而 π ( 右 ∣ s t ; θ ) \pi(右|s_t;\theta) π(右∣st;θ)变小。
带基线的 REINFORCE 算法
上一节推导出了带基线的策略梯度,并且对策略梯度做了蒙特卡洛近似。本节中,我们使用状态价值 V π ( s ) V_{\pi}(s) Vπ(s) 作基线,得到策略梯度的一个无偏估计:
g ( s , a ; θ ) = [ Q π ( s , a ) − V π ( s ) ] ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boxed{\boldsymbol{g}(s,a;\boldsymbol{\theta})=\left[Q_{\pi}(s,a)-V_{\pi}(s)\right]\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a|s;\boldsymbol{\theta}).} g(s,a;θ)=[Qπ(s,a)−Vπ(s)]⋅∇θlnπ(a∣s;θ).
我们在深度强化学习(王树森)笔记03: 主要介绍policy network, policy gradient,REINFORCE 中学过 REINFORCE, 它使用实际观测的回报 u u u 来代替动作价值 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)。 此处我们同样用 u u u 代替 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)。此外,我们还用一个神经网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w) 近似状态价值函数 V π ( s ) V_{\pi}(s) Vπ(s)。这样一来, g ( s , a ; θ ) g(s,a;\theta) g(s,a;θ) 就被近似成了:
g ~ ( s , a ; θ ) = [ u − v ( s ; w ) ] ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boxed{\quad\tilde{\boldsymbol{g}}(s,a;\boldsymbol{\theta})=\left[u-v(s;\boldsymbol{w})\right]\cdot\nabla_\theta\ln\pi(a|s;\boldsymbol{\theta}).} g~(s,a;θ)=[u−v(s;w)]⋅∇θlnπ(a∣s;θ).
可以用 g ~ ( s , a ; θ ) \tilde{g}(s,a;\boldsymbol{\theta}) g~(s,a;θ) 作为策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ) 的近似,更新策略网络参数:
θ ← θ + β ⋅ g ~ ( s , a ; θ ) \theta\:\leftarrow\:\theta\:+\:\beta\cdot\tilde{\boldsymbol{g}}(s,a;\:\boldsymbol{\theta}) θ←θ+β⋅g~(s,a;θ)
策略网络和价值网络
带基线的 REINFORCE 需要两个神经网络:策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 和价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w) ;
神经网络结构如图 8.2 和 8.3 所示。策略网络与之前章节一样:输入是状态 s s s, 输出是一个向量,每个元素表示一个动作的概率。

此处的价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w) 与之前使用的价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w) 区别较大。此处的 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w) 是对状态价值 V π V_\mathrm{\pi} Vπ的近似,而非对动作价值 Q π Q_\mathrm{\pi} Qπ 的近似。 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w) 的输入是状态 s s s, 输出是一个实数,作为基线。策略网络和价值网络的输入都是状态 s s s,因此可以让两个神经网络共享卷积网络的参数,这是编程实现中常用的技巧。
虽然带基线的 REINFOKCE 有一个策略网络和一个价值网络,但是这种方法不是actor-critic。价值网络没有起到“评委”的作用,只是作为基线而已,目的在于降低方差,加速收敛。真正帮助策略网络(演员)改进参数 θ \theta θ(演员的演技)的不是价值网络,而是实际观测到的回报 u u u 。
算法的推导
训练策略网络的方法是近似的策略梯度上升。从 t t t 时刻开始,智能体完成一局游戏,观测到全部奖励 r t , r t + 1 , ⋯ , r n r_t,r_{t+1},\cdots,r_n rt,rt+1,⋯,rn,然后计算回报 u t = ∑ k = t n γ k − t ⋅ r k u_t=\sum_{k=t}^n\gamma^{k-t}\cdot r_k ut=∑k=tnγk−t⋅rk。让价值网络做出预测 v ^ t = v ( s t ; w ) \widehat{v}_t=v(s_t;\boldsymbol{w}) v t=v(st;w), 作为基线。这样就得到了带基线的策略梯度:
g ~ ( s t , a t ; θ ) = ( u t − v ^ t ) ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \tilde{\boldsymbol{g}}\big(s_{t},a_{t};\:\boldsymbol{\theta}\big)\:=\:\big(\:u_{t}-\widehat{v}_{t}\big)\:\cdot\:\nabla_{\boldsymbol{\theta}}\:\ln\pi\big(a_{t}\big|\:s_{t};\:\boldsymbol{\theta}\big). g~(st,at;θ)=(ut−v t)⋅∇θlnπ(at st;θ).
它是策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ) 的近似。最后做梯度上升更新 θ : \theta: θ:
θ ← θ + β ⋅ g ~ ( s t , a t ; θ ) . \theta\:\leftarrow\:\theta+\beta\cdot\tilde{\boldsymbol{g}}(s_{t},a_{t};\:\theta). θ←θ+β⋅g~(st,at;θ).
这样可以让目标函数 J ( θ ) J(\boldsymbol{\theta}) J(θ) 逐渐增大。
训练价值网络的方法是回归 (regression)。回忆一下,状态价值是回报的期望:
V π ( s t ) = E [ U t ∣ S t = s t ] , V_\pi(s_t)=\mathbb{E}[U_t|S_t=s_t], Vπ(st)=E[Ut∣St=st],
期望消掉了动作 A t , A t + 1 , ⋯ , A n A_t,A_{t+1},\cdots,A_n At,At+1,⋯,An 和状态 S t + 1 , ⋯ , S n S_{t+1},\cdots,S_n St+1,⋯,Sn。训练价值网络的目的是让 v ( s t ; w ) v(s_t;\boldsymbol{w}) v(st;w) 拟合 V π ( s t ) V_\pi(s_t) Vπ(st),即拟合 u t u_t ut 的期望。定义损失函数:
L ( w ) = 1 2 n ∑ t = 1 n [ v ( s t ; w ) − u t ] 2 . L(\boldsymbol{w})\:=\:\frac{1}{2n}\sum_{t=1}^{n}\big[v(s_{t};\boldsymbol{w})\:-\:u_{t}\big]^{2}. L(w)=2n1t=1∑n[v(st;w)−ut]2.
设 v ^ t = v ( s t ; w ) \widehat{v}_t=v(s_t;w) v t=v(st;w)。损失函数的梯度是:
∇ w L ( w ) = 1 n ∑ t = 1 n ( v ^ t − u t ) ⋅ ∇ w v ( s t ; w ) . \nabla_{\boldsymbol{w}}L(\boldsymbol{w})\:=\:\frac{1}{n}\sum_{t=1}^{n}\left(\widehat{v}_{t}-u_{t}\right)\:\cdot\:\nabla_{\boldsymbol{w}}v(s_{t};\boldsymbol{w}). ∇wL(w)=n1t=1∑n(v t−ut)⋅∇wv(st;w).
做一次梯度下降更新 w w w:
w ← w − α ⋅ ∇ w L ( w ) . w\:\leftarrow\:w\:-\:\alpha\cdot\nabla_{\boldsymbol{w}}L(\boldsymbol{w}). w←w−α⋅∇wL(w).
训练流程
当前策略网络的参数是 θ n o w \theta_\mathrm{now} θnow,价值网络的参数是 w n o w w_\mathrm{now} wnow。执行下面的步骤,对参数做一轮更新。
- 用策略网络 θ n o w \theta_\mathrm{now} θnow 控制智能体从头开始玩一局游戏,得到一条轨迹 (trajectory):
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , ⋯ , s n , a n , r n . s_{1},a_{1},r_{1},\quad s_{2},a_{2},r_{2},\quad\cdots,\quad s_{n},a_{n},r_{n}. s1,a1,r1,s2,a2,r2,⋯,sn,an,rn.
- 计算所有的回报:
u t = ∑ k = t n γ k − t ⋅ r k , ∀ t = 1 , ⋯ , n . u_{t}\:=\:\sum_{k=t}^{n}\gamma^{k-t}\cdot r_{k},\quad\forall\:t=1,\cdots,n. ut=k=t∑nγk−t⋅rk,∀t=1,⋯,n.
-
让价值网络做预测:
v ^ t = v ( s t ; w n o w ) , ∀ t = 1 , ⋯ , n . \widehat v_{t}\:=\:v(s_{t};\boldsymbol{w_{\mathrm{now}}}),\quad\forall\:t=1,\cdots,n. v t=v(st;wnow),∀t=1,⋯,n. -
计算误差 δ t = v t ^ − u t , ∀ t = 1 , ⋯ , n \delta_t=\widehat{v_t}-u_t,\:\forall t=1,\cdots,n δt=vt −ut,∀t=1,⋯,n。
-
用 { s t } t = 1 n \{s_t\}_{t=1}^n {st}t=1n 作为价值网络输入,做反向传播计算:
∇ w v ( s t ; w n o w ) , ∀ t = 1 , ⋯ , n . \nabla_{\boldsymbol{w}}\:v\big(s_{t};\:\boldsymbol{w}_{\mathrm{now}}\big),\quad\forall\:t=1,\cdots,n. ∇wv(st;wnow),∀t=1,⋯,n. -
更新价值网络参数:
w n e w ← w n o w − α ⋅ ∑ t = 1 n δ t ⋅ ∇ w v ( s t ; w n o w ) . w_{\mathrm{new}}\:\leftarrow\:w_{\mathrm{now}}\:-\:\alpha\cdot\sum_{t=1}^{n}\delta_{t}\cdot\nabla_{\boldsymbol{w}}\:v\big(s_{t};\:\boldsymbol{w_{\mathrm{now}}}\big). wnew←wnow−α⋅t=1∑nδt⋅∇wv(st;wnow). -
用 { ( s t , a t ) } t = 1 n \{(s_t,a_t)\}_{t=1}^n {(st,at)}t=1n 作为数据,做反向传播计算:
∇ θ ln π ( a t ∣ s t ; θ n o w ) , ∀ t = 1 , ⋯ , n . \nabla_{\boldsymbol{\theta}}\ln\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta}_{\mathrm{now}}),\quad\forall\:t=1,\cdots,n. ∇θlnπ(at∣st;θnow),∀t=1,⋯,n.
8. 做随机梯度上升更新策略网络参数:
θ n e w ← θ n o w − β ⋅ ∑ t = 1 n γ t − 1 ⋅ δ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ n o w ) ⏟ 负的近似梯度 − g ~ ( s t , a t ; θ n o w ) . \theta_{\mathrm{new}}\:\leftarrow\:\theta_{\mathrm{now}}\:-\:\beta\:\cdot\:\sum_{t=1}^{n}\gamma^{t-1}\:\cdot\:\underbrace{\delta_{t}\:\cdot\:\nabla_{\theta}\ln\pi(a_{t}\:\big|\:s_{t};\:\theta_{\mathrm{now}}\big)}_{\text{负的近似梯度 }-\tilde{g}(s_{t},a_{t};\boldsymbol{\theta_{\mathrm{now}}})}\:. θnew←θnow−β⋅t=1∑nγt−1⋅负的近似梯度 −g~(st,at;θnow) δt⋅∇θlnπ(at st;θnow).
Advantage Actor-Critic (A2C)
之前我们推导出了带基线的策略梯度,并且对策略梯度做了蒙特卡洛近似,得到策略梯度的一个无偏估计:
g ( s , a ; θ ) = [ Q π ( s , a ) − V π ( s ) ⏟ 优势函数 ] ⋅ ∇ θ ln π ( a ∣ s ; θ ) . ( 8.2 ) \boldsymbol{g}(s,a;\boldsymbol{\theta})=\left[\underbrace{Q_{\pi}(s,a)-V_{\pi}(s)}_{\text{优势函数}}\right]\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a|s;\boldsymbol{\theta}).\quad{(8.2)} g(s,a;θ)= 优势函数 Qπ(s,a)−Vπ(s) ⋅∇θlnπ(a∣s;θ).(8.2)
公式中的 Q π − V π Q_\pi-V_\pi Qπ−Vπ 被称作优势函数 (advantage function)。因此,基于上面公式得到的actor-critic 方法被称为 advantage actor-critic, 缩写 A2C。
A2C 属于 actor-critic 方法。有一个策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ),相当于演员,用于控制智能体运动。还有一个价值网络 v ( s ; w ) v(s;w) v(s;w),相当于评委,他的评分可以帮助策略网络 (演员) 改进技术。两个神经网络的结构与上一节中的完全相同,但是本节和上一节用不同的方法训练两个神经网络。
算法推导
训练价值网络:训练价值网络 v ( s ; w ) v(s;w) v(s;w) 的算法是从贝尔曼公式来的:
V π ( s t ) = E A t ∼ π ( ⋅ ∣ s t ; θ ) [ E S t + 1 ∼ p ( ⋅ ∣ s t , A t ) [ R t + γ ⋅ V π ( S t + 1 ) ] ] . V_{\pi}(s_{t})\:=\:\mathbb{E}_{A_{t}\sim\pi(\cdot|s_{t};\theta)}\Big[\mathbb{E}_{S_{t+1}\sim p(\cdot|s_{t},A_{t})}\Big[R_{t}\:+\:\gamma\cdot V_{\pi}\big(S_{t+1}\big)\Big]\Big]. Vπ(st)=EAt∼π(⋅∣st;θ)[ESt+1∼p(⋅∣st,At)[Rt+γ⋅Vπ(St+1)]].
我们对贝尔曼方程左右两边做近似:
- 方程左边的 V π ( s t ) V_\pi(s_t) Vπ(st)可以近似成 v ( s t ; w ) v(s_t;\boldsymbol{w}) v(st;w)。 v ( s t ; w ) v(s_t;\boldsymbol{w}) v(st;w) 是价值网络在 t t t 时刻对 V π ( s t ) V_\pi(s_t) Vπ(st) 做出的估计。
- 方程右边的期望是关于当前时刻动作 A t A_t At 与下一时刻状态 S t + 1 S_{t+1} St+1 求的。给定当前状态 s t s_t st,智能体执行动作 a t a_t at,环境会给出奖励 r t r_t rt 和新的状态 s t + 1 s_{t+1} st+1。用观测到的 r t r_t rt、 s t + 1 s_{t+1} st+1 对期望做蒙特卡洛近似,得到:
r t + γ ⋅ V π ( s t + 1 ) . ( 8.3 ) r_{t}+\gamma\cdot V_{\pi}(s_{t+1}). \quad(8.3) rt+γ⋅Vπ(st+1).(8.3)
- 进一步把公式 (8.3) 中的 V π ( s t + 1 ) V_{\pi}(s_{t+1}) Vπ(st+1) 近似成 v ( s t + 1 ; w ) v(s_{t+1};\boldsymbol{w}) v(st+1;w), 得到
y ^ t ≜ r t + γ ⋅ v ( s t + 1 ; w ) . \boxed{\widehat{y}_{t}\triangleq r_{t}+\gamma\cdot v(s_{t+1};\boldsymbol{w}).} y t≜rt+γ⋅v(st+1;w).
把它称作 TD 目标。它是价值网络在 t + 1 t+1 t+1 时刻对 V π ( s t ) V_{\pi}(s_t) Vπ(st) 做出的估计。
v ( s t ; w ) v(s_t;\boldsymbol{w}) v(st;w) 和 y ^ t \widehat{y}_t y t 都是对动作价值 V π ( s t ) V_{\pi}(s_t) Vπ(st) 的估计。由于 y ^ t \widehat{y}_t y t 部分基于真实观测到的奖励 r t r_t rt,我们认为 y ^ t \widehat{y}_t y t 比 v ( s t ; w ) v(s_t;w) v(st;w) 更可靠。所以把 y ^ t \widehat{y}_t y t 固定住,更新 w w w, 使得 v ( s t ; w ) v(s_t;\boldsymbol{w}) v(st;w) 更接近 y ^ t \widehat{y}_t y t 。
具体这样更新价值网络参数 w w w。定义损失函数
L ( w ) ≜ 1 2 [ v ( s t ; w ) − y ^ t ] 2 . L(\boldsymbol{w})\:\triangleq\:\frac{1}{2}\Big[v(s_{t};\boldsymbol{w})\:-\:\widehat{y}_{t}\Big]^{2}. L(w)≜21[v(st;w)−y t]2.
设 v ^ t ≜ v ( s t ; w ) \widehat{v}_t\triangleq v(s_t;w) v t≜v(st;w)。损失函数的梯度是:
∇ w L ( w ) = ( v ^ t − y ^ t ) ⏟ T D 误差 δ t ⋅ ∇ w v ( s t ; w ) . \nabla_{\boldsymbol{w}}L\big(\boldsymbol{w}\big)\:=\:\underbrace{\left(\widehat{v}_{t}-\widehat{y}_{t}\right)}_{\mathrm{TD~}\text{误差 }\delta_{t}}\cdot\nabla_{\boldsymbol{w}}\:v\big(s_{t};\boldsymbol{w}\big). ∇wL(w)=TD 误差 δt (v t−y t)⋅∇wv(st;w).
定义 TD 误差为 δ t ≜ v ^ t − y ^ t \delta_t\triangleq\widehat{v}_t-\widehat{y}_t δt≜v t−y t。做一轮梯度下降更新 w : w: w:
w ← w − α ⋅ δ t ⋅ ∇ w v ( s t ; w ) . \boxed{\boldsymbol{w}\:\leftarrow\:\boldsymbol{w}\:-\:\alpha\cdot\delta_{t}\:\cdot\:\nabla_{\boldsymbol{w}}\:v(s_{t};\boldsymbol{w}).} w←w−α⋅δt⋅∇wv(st;w).
这样可以让价值网络的预测 v ( s t ; w ) v(s_t;\boldsymbol{w}) v(st;w) 更接近 y ^ t \widehat{y}_t y t。
训练策略网络:A2C 从公式 (8.2)出发,对 g ( s , a ; θ ) g(s,a;\theta) g(s,a;θ) 做近似,记作 g ~ \tilde{g} g~, 然后用 g ~ \tilde{g} g~ 更新策略网络参数 θ \theta θ。下面我们做数学推导。回忆一下贝尔曼公式:
Q π ( s t , a t ) = E S t + 1 ∼ p ( ⋅ ∣ s t , a t ) [ R t + γ ⋅ V π ( S t + 1 ) ] . Q_{\pi}\big(s_{t},a_{t}\big)\:=\:\mathbb{E}_{S_{t+1}\sim p(\cdot|s_{t},a_{t}\big)}\Big[\:R_{t}\:+\:\gamma\cdot V_{\pi}\big(S_{t+1}\big)\:\Big]. Qπ(st,at)=ESt+1∼p(⋅∣st,at)[Rt+γ⋅Vπ(St+1)].
把近似策略梯度 g ( s t , u t ; θ ) g(s_t,u_t;\boldsymbol{\theta}) g(st,ut;θ) 中的 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at) 替换成上面的期望,得到:
g ( s t , a t ; θ ) = [ Q π ( s t , a t ) − V π ( s t ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) = [ E S t + 1 [ R t + γ ⋅ V π ( S t + 1 ) ] − V π ( s t ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \begin{aligned} \boldsymbol{g}(s_{t},a_{t};\boldsymbol{\theta})& =\left[Q_{\pi}\left(s_{t},a_{t}\right)-V_{\pi}\big(s_{t}\big)\right]\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a_{t}|s_{t};\boldsymbol{\theta}) \\ &\begin{array}{rcl}{=}&{{}\left[\mathbb{E}_{S_{t+1}}\right[R_{t}+\gamma\cdot V_{\pi}\big(S_{t+1}\big)]-V_{\pi}\big(s_{t}\big)]\cdot\nabla_{\theta}\ln\pi\big(a_{t}\big|s_{t};\theta\big).}\end{array} \end{aligned} g(st,at;θ)=[Qπ(st,at)−Vπ(st)]⋅∇θlnπ(at∣st;θ)=[ESt+1[Rt+γ⋅Vπ(St+1)]−Vπ(st)]⋅∇θlnπ(at st;θ).
当智能体执行动作 a t a_t at 之后,环境给出新的状态 s t + 1 s_{t+1} st+1 和奖励 r t r_t rt; 利用 s t + 1 s_{t+1} st+1 和 r t r_t rt 对上面的期望做蒙特卡洛近似,得到:
g ( s t , a t ; θ ) ≈ [ r t + γ ⋅ V π ( s t + 1 ) − V π ( s t ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \begin{array}{rcl}g(s_t,a_t;\:\theta)&\approx&\Big[\:r_t\:+\:\gamma\cdot V_\pi\big(s_{t+1}\big)\:-\:V_\pi\big(s_t\big)\:\Big]\:\cdot\:\nabla_\theta\:\ln\pi\big(a_t\:\big|\:s_t;\:\theta\big).\end{array} g(st,at;θ)≈[rt+γ⋅Vπ(st+1)−Vπ(st)]⋅∇θlnπ(at st;θ).
进一步把状态价值函数 V π ( s ) V_{\pi}(s) Vπ(s) 替换成价值网络 v ( s ; w ) v(s;w) v(s;w), 得到:
g ~ ( s t , a t ; θ ) ≜ [ r t + γ ⋅ v ( s t + 1 ; w ) ⏟ TD 目标 y ^ t − v ( s t ; w ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \begin{array}{rcl}\tilde{\boldsymbol{g}}(s_t,a_t;\boldsymbol{\theta})&\triangleq&\Big[\underbrace{r_t\:+\:\gamma\cdot v(s_{t+1};\boldsymbol{w})}_{\text{TD 目标 }\widehat{y}_t}-v(s_t;\boldsymbol{w})\:\Big]\:\cdot\:\nabla_{\boldsymbol{\theta}}\ln\pi(a_t\:|\:s_t;\boldsymbol{\theta}).\end{array} g~(st,at;θ)≜[TD 目标 y t rt+γ⋅v(st+1;w)−v(st;w)]⋅∇θlnπ(at∣st;θ).
前面定义了 TD 目标和 TD 误差:
y ^ t ≜ r t + γ ⋅ v ( s t + 1 ; w ) 和 δ t ≜ v ( s t ; w ) − y ^ t . \widehat{y}_{t}\:\triangleq\:r_{t}\:+\:\gamma\cdot v(s_{t+1};\:\boldsymbol{w})\quad\text{和}\quad\delta_{t}\:\triangleq\:v(s_{t};\:\boldsymbol{w})\:-\:\widehat{y}_{t}. y t≜rt+γ⋅v(st+1;w)和δt≜v(st;w)−y t.
因此,可以把 g ~ \tilde{g} g~写成:
g ~ ( s t , a t ; θ ) ≜ − δ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \boxed{\tilde{\boldsymbol{g}}(s_t,a_t;\boldsymbol{\theta})\triangleq-\delta_t\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a_t|s_t;\boldsymbol{\theta}).} g~(st,at;θ)≜−δt⋅∇θlnπ(at∣st;θ).
g ~ \tilde{g} g~ 是 g g g 的近似,所以也是策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ) 的近似。用 g ~ \tilde{g} g~ 更新策略网络参数 θ \theta θ:
θ ← θ + β ⋅ g ~ ( s t , a t ; θ ) . \theta\:\leftarrow\:\theta\:+\:\beta\cdot\tilde{\boldsymbol{g}}\left(s_t,a_t;\:\boldsymbol{\theta}\right). θ←θ+β⋅g~(st,at;θ).
这样可以让目标函数 J ( θ ) J(\theta) J(θ) 变大。
策略网络与价值网络的关系 : A2C 中策略网络 (演员) 和价值网络 (评委) 的关系如图 8.4 所示。

智能体由策略网络 π 控制,与环境交互,并收集状态、动作、奖励。策略网络(演员) 基于状态 s t s_t st 做出动作 a t a_t at。价值网络 (评委) 基于 s t s_t st、 s t + 1 s_{t+1} st+1、 r t r_t rt 算出 TD 误差 δ t \delta_t δt。策略网络(演员) 依靠 δ t \delta_t δt 来判断自己动作的好坏,从而改进自己的演技 (即参数 θ \theta θ)。
读者可能会有疑问: 价值网络 v v v 只知道两个状态 s t s_t st、 s t + 1 s_{t+1} st+1,而并不知道动作 a t a_t at,那么价值网络为什么能评价 a t a_t at 的好坏呢?价值网络 v v v 告诉策略网络 π \pi π 的唯一信息是 δ t \delta_{t} δt。回顾一下 δ t \delta_t δt 的定义:
− δ t = r t + γ ⋅ v ( s t + 1 ; w ) ⏟ TD 目标 y ^ t − v ( s t ; w ) ⏟ 基线 . \begin{array}{rcl}-\delta_t&=&\underbrace{r_t\:+\:\gamma\cdot v(s_{t+1};\:\boldsymbol{w})}_{\text{TD 目标}\:\widehat{y}_t}\:-\:\underbrace{v(s_t;\:\boldsymbol{w})}_\text{基线}.\end{array} −δt=TD 目标y t rt+γ⋅v(st+1;w)−基线 v(st;w).
基线 v ( s t ; w ) v(s_t;\boldsymbol{w}) v(st;w) 是价值网络在 t t t 时刻对 E [ U t ] \mathbb{E}[U_t] E[Ut] 的估计;此时智能体尚未执行动作 a t a_t at。而 TD 目标 y ^ t \widehat{y}_t y t 是价值网络在 t + 1 t+1 t+1 时刻对 E [ U t ] \mathbb{E}[U_t] E[Ut] 的估计;此时智能体已经执行动作 a t a_t at 。
- 如果 y ^ t > v ( s t ; w ) \widehat{y}_t>v(s_t;\boldsymbol{w}) y t>v(st;w),说明动作 a t a_t at 很好,使得奖励 r t r_t rt 超出预期,或者新的状态 s t + 1 s_{t+1} st+1 比预期好;这种情况下应该更新 θ \theta θ,使得 π ( a t ∣ s t ; θ ) \pi(a_t|s_t;\theta) π(at∣st;θ) 变大。
- 如果 y ^ t < v ( s t ; w ) \widehat{y}_t<v(s_t;\boldsymbol{w}) y t<v(st;w),说明动作 a t a_t at 不好,导致奖励 r t r_t rt不及预期,或者新的状态 s t + 1 s_{t+1} st+1比预期差;这种情况下应该更新 θ \theta θ,使得 π ( a t ∣ s t ; θ ) \pi(a_t|s_t;\theta) π(at∣st;θ) 减小。
综上所述, δ t \delta_t δt 中虽然不包含动作 a t a_t at,但是 δ t \delta_t δt 可以间接反映出动作 a t a_t at 的好坏,可以帮助策略网络(演员) 改进演技。
训练流程
下面概括 A2C 训练流程。设当前策略网络参数是 θ n o w \theta_\mathrm{now} θnow,价值网络参数是 w n o w w_\mathrm{now} wnow。执行下面的步骤,将参数更新成 θ n e w \theta_\mathrm{new} θnew 和 w n e w w_\mathrm{new} wnew:
-
观测到当前状态 s t s_t st,根据策略网络做决策 : a t ∼ π ( ⋅ ∣ s t ; θ n o w ) :a_t\sim\pi(\cdot|s_t;\theta_\mathrm{now}) :at∼π(⋅∣st;θnow),并让智能体执行动作 a t a_t at。
-
从环境中观测到奖励 r t r_t rt 和新的状态 s t + 1 s_{t+1} st+1。
-
让价值网络打分:
v t ^ = v ( s t ; w n o w ) 和 v ^ t + 1 = v ( s t + 1 ; w n o w ) \widehat{v_{t}}\:=\:v\big(s_{t};\:\boldsymbol{w_{\mathrm{now}}}\big)\quad\text{和}\quad\widehat{v}_{t+1}\:=\:v\big(s_{t+1};\:\boldsymbol{w_{\mathrm{now}}}\big) vt =v(st;wnow)和v t+1=v(st+1;wnow)
- 计算 TD 目标和 TD 误差:
y t ^ = r t + γ ⋅ v ^ t + 1 和 δ t = v ^ t − y ^ t . \widehat{y_{t}}\:=\:r_{t}+\gamma\cdot\widehat{v}_{t+1}\quad\text{和}\quad\delta_{t}\:=\:\widehat{v}_{t}-\widehat{y}_{t}. yt =rt+γ⋅v t+1和δt=v t−y t.
- 更新价值网络:
w n e w ← w n o w − α ⋅ δ t ⋅ ∇ w v ( s t ; w n o w ) . w_{\mathrm{new}}\:\leftarrow\:w_{\mathrm{now}}\:-\:\alpha\cdot\delta_{t}\cdot\nabla_{\boldsymbol{w}}v\left(s_{t};\:\boldsymbol{w_{\mathrm{now}}}\right). wnew←wnow−α⋅δt⋅∇wv(st;wnow).
- 更新策略网络:
θ n e w ← θ n o w − β ⋅ δ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ n o w ) . \theta_{\mathrm{new}}\:\leftarrow\:\theta_{\mathrm{now}}\:-\:\beta\cdot\delta_{t}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta}_{\mathrm{now}}). θnew←θnow−β⋅δt⋅∇θlnπ(at∣st;θnow).
注 此处训练策略网络和价值网络的方法属于同策略(on-policy),要求行为策略(behavion policy)与目标策略 (target policy) 相同,都是最新的策略网络 π ( a ∣ s ; θ n o w ) \pi(a|s;\theta_\mathrm{now}) π(a∣s;θnow)。不能使用经验回放,因为经验回放数组中的数据是用旧的策略网络 π ( a ∣ s ; θ o l d ) \pi(a|s;\theta_\mathrm{old}) π(a∣s;θold) 获取的,不能在当前重复利用。
用目标网络改进训练
上述训练价值网络的算法存在自举——即用价值网络自己的估值 v ^ t + 1 \widehat{v}_{t+1} v t+1去更新价值网络自己。为了缓解自举造成的偏差,可以使用目标网络(target network) 计算 TD 目标。把目标网络记作 v ( s ; w − ) v(s;w^-) v(s;w−), 它的结构与价值网络的结构相同,但是参数不同。使用目标网络计算 TD 目标,那么 A2C 的训练就变成了:
- 观测到当前状态 s t s_t st,根据策略网络做决策 : a t ∼ π ( ⋅ ∣ s t ; θ n o w ) :a_t\sim\pi(\cdot|s_t;\theta_\mathrm{now}) :at∼π(⋅∣st;θnow), 并让智能体执行动作 a t a_t at。
- 从环境中观测到奖励 r t r_t rt 和新的状态 s t + 1 s_{t+1} st+1。
- 让价值网络给 s t s_t st 打分:
v t ^ = v ( s t ; w n o w ) . \widehat{v_{t}}\:=\:v\big(s_{t};\:\boldsymbol{w_{\mathrm{now}}}\big). vt =v(st;wnow).
- 让目标网络给 s t + 1 s_{t+1} st+1 打分:
v ^ t + 1 − = v ( s t + 1 ; w n o w − ) . \widehat v_{t+1}^{-}\:=\:v\big(s_{t+1};\:\boldsymbol{w_{\mathrm{now}}^{-}}\big). v t+1−=v(st+1;wnow−).
- 计算 TD 目标和 TD 误差:
y ^ t − = r t + γ ⋅ v ^ t + 1 − 和 δ t = v ^ t − y ^ t − . \widehat{y}_{t}^{-}\:=\:r_{t}+\gamma\cdot\widehat{v}_{t+1}^{-}\quad\text{和}\quad\delta_{t}\:=\:\widehat{v}_{t}-\widehat{y}_{t}^{-}. y t−=rt+γ⋅v t+1−和δt=v t−y t−.
- 更新价值网络:
w n e w ← w n o w − α ⋅ δ t ⋅ ∇ w v ( s t ; w n o w ) . w_{\mathrm{new}}\:\leftarrow\:w_{\mathrm{now}}-\alpha\cdot\delta_{t}\cdot\nabla_{\boldsymbol{w}}v\big(s_{t};\:\boldsymbol{w}_{\mathrm{now}}\big). wnew←wnow−α⋅δt⋅∇wv(st;wnow).
- 更新策略网络:
θ n e w ← θ n o w − β ⋅ δ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ n o w ) . \theta_{\mathrm{new}}\:\leftarrow\:\theta_{\mathrm{now}}\:-\:\beta\cdot\delta_{t}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta}_{\mathrm{now}}). θnew←θnow−β⋅δt⋅∇θlnπ(at∣st;θnow).
- 设 τ ∈ ( 0 , 1 ) \tau\in(0,1) τ∈(0,1) 是需要手动调的超参数。做加权平均更新目标网络的参数:
w n e w ˉ ← τ ⋅ w n e w + ( 1 − τ ) ⋅ w n o w − . \bar{w_{\mathrm{new}}}\:\leftarrow\:\tau\cdot w_{\mathrm{new}}\:+\:\left(1-\tau\right)\cdot\boldsymbol{w_{\mathrm{now}}^{-}}. wnewˉ←τ⋅wnew+(1−τ)⋅wnow−.
总结
-
在策略梯度中加入基线 (baseline) 可以降低方差,显著提升实验效果。实践中常用 b = V π ( s ) b=V_{\pi}(s) b=Vπ(s) 作为基线。
-
可以用基线来改进 REINFORCE 算法。价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w) 近似状态价值函数 V π ( s ) V_\pi(s) Vπ(s) ,把 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w) 作为基线。用策略梯度上升来更新策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ)。用蒙特卡洛(而非自举) 来更新价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w)。
-
可以用基线来改进 actor-critic, 得到的方法叫做 advantage actor-critic(A2C),它也有一个策略网络 π ( a ∣ s ; θ ) \pi(a|s;\boldsymbol{\theta}) π(a∣s;θ) 和一个价值网络 v ( s ; θ ) v(s;\boldsymbol{\theta}) v(s;θ)。用策略梯度上升来更新策略网络,用 TD 算法来更新价值网络。
后记
截至2024年1月29日20点11分,学习完这一章的内容:带baseline的策略梯度方法。明天是最后学习的一天,看是否能够结束这个系列。
相关文章:

深度强化学习(王树森)笔记09
深度强化学习(DRL) 本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。 参考链接 Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL 源代码链接:https://github.c…...
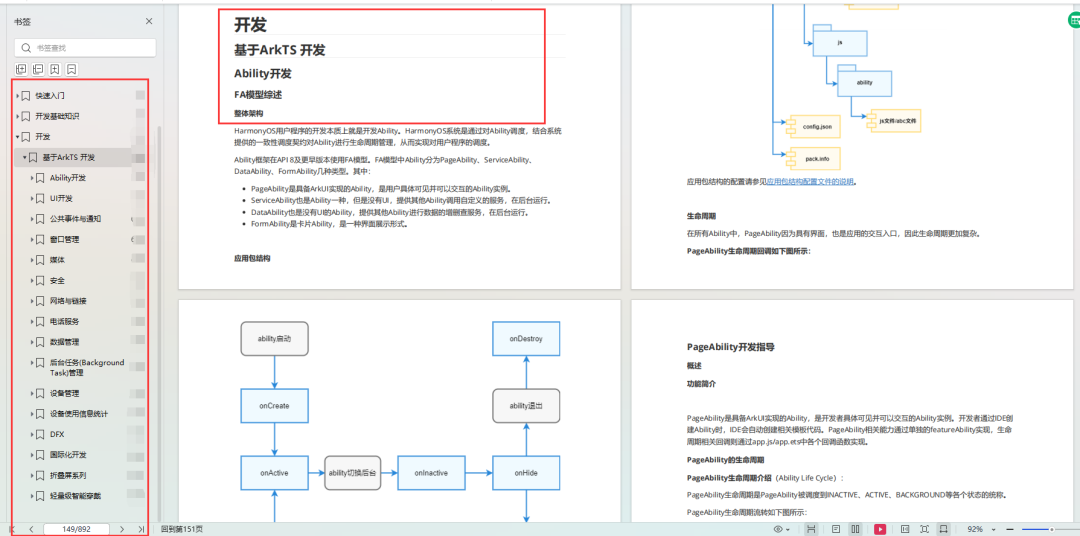
调试OpenHarmony应用/服务
调试流程 DevEco Studio提供了丰富的OpenHarmony应用/服务调试能力,帮助开发者更方便、高效的调试应用/服务。 OpenHarmony应用/服务调试支持使用真机设备调试。使用真机设备进行调试前,需要对HAP进行签名后进行调试。详细的调试流程如下图所示&#x…...

【NGINX】NGINX如何阻止指定ip的请求
业务场景: web页面做了一个功能,在websocket请求失败的情况,会定时向服务端进行重试进行建立连接。 存在的问题是即使这个web系统没人操作的情况下,只要页面没有关闭,即使系统超时了页面也没有发生跳转,这…...

PHP抽奖设置中奖率,以及防高并发
一、中奖率,先在后台设定好奖项名称,抽奖份数,以及中奖百分比 奖品表draw 二、 借助文件排他锁,在处理下单请求的时候,用flock锁定一个文件,如果锁定失败说明有其他订单正在处理,此时要么等待要么直接提示用户"服务器繁忙" 阻塞(等待)模式,一般都是用这个模…...

使用.NET6 Avalonia开发跨平台三维应用
本文介绍在Vistual Studio 2022中使用Avalonia和集成AnyCAD Rapid AvaloniaUI三维控件的过程。 0 初始化环境 安装Avalonia.Templates dotnet new install Avalonia.Templates若之前安装过可忽略此步骤。 1 创建项目 选择创建AvaloniaUI项目 选一下.NET6版本和Avalonia版…...
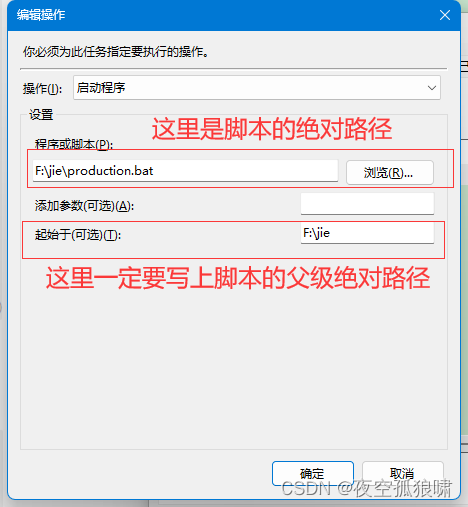
linux(ubuntu)中crontab定时器命令详解 以及windows中定时器
文章目录 linux(ubuntu)中crontab定时器命令详解基本语法crontab 文件格式通配符示例在Ubuntu中,定时任务cron服务默认被安装。可以通过以下命令操作该服务:其他注意事项windows中定时器任务的创建步骤:常规触发器操作…...
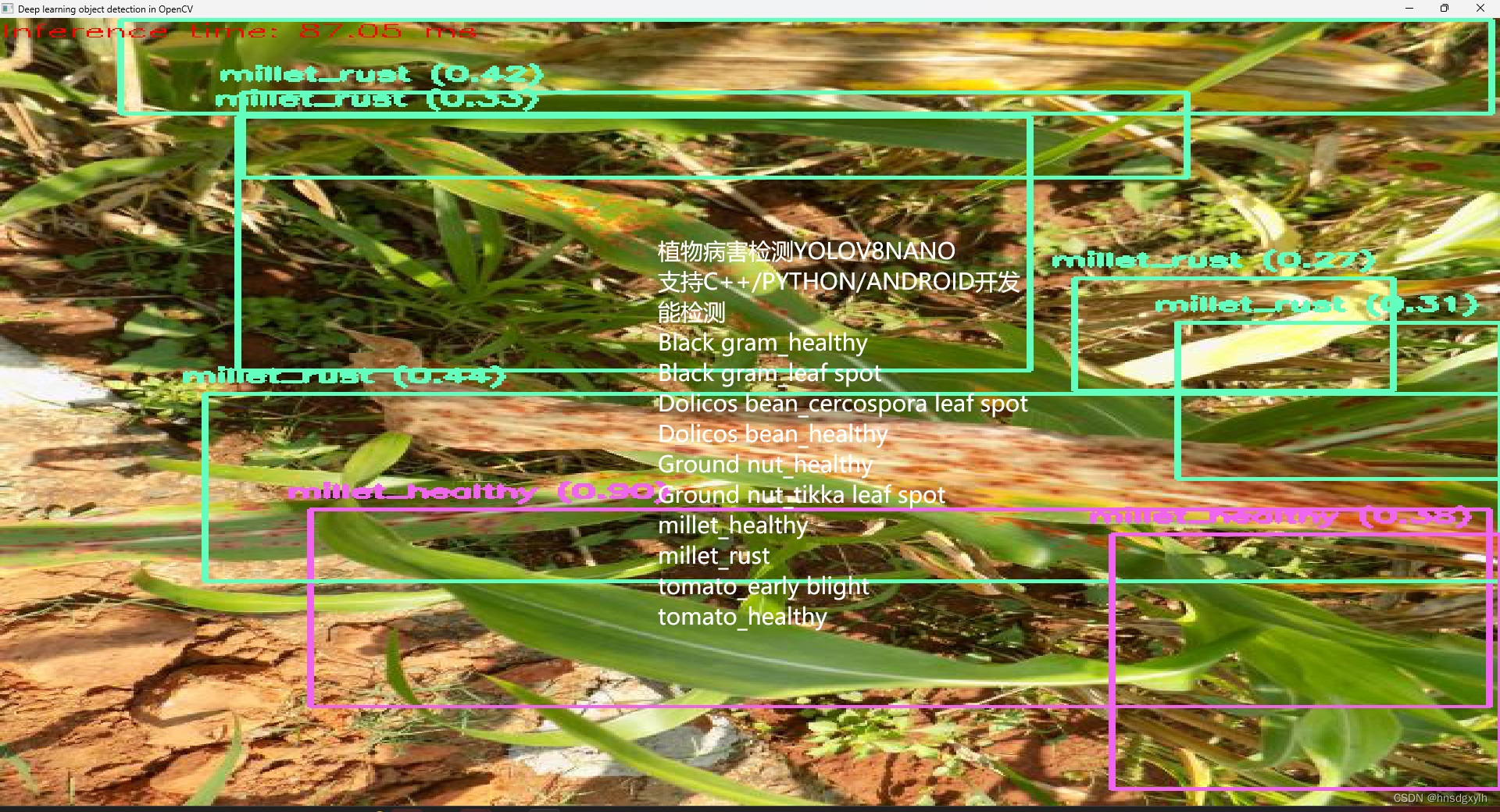
植物病害检测YOLOV8,OPENCV调用
【免费】植物病害检测,10种类型,YOLOV8训练,转换成ONNX,OPENCV调用资源-CSDN文库 植物病害检测,YOLOV8NANO,训练得到PT模型,然后转换成ONNX,OPENCV的DNN调用,支持C,PYTH…...
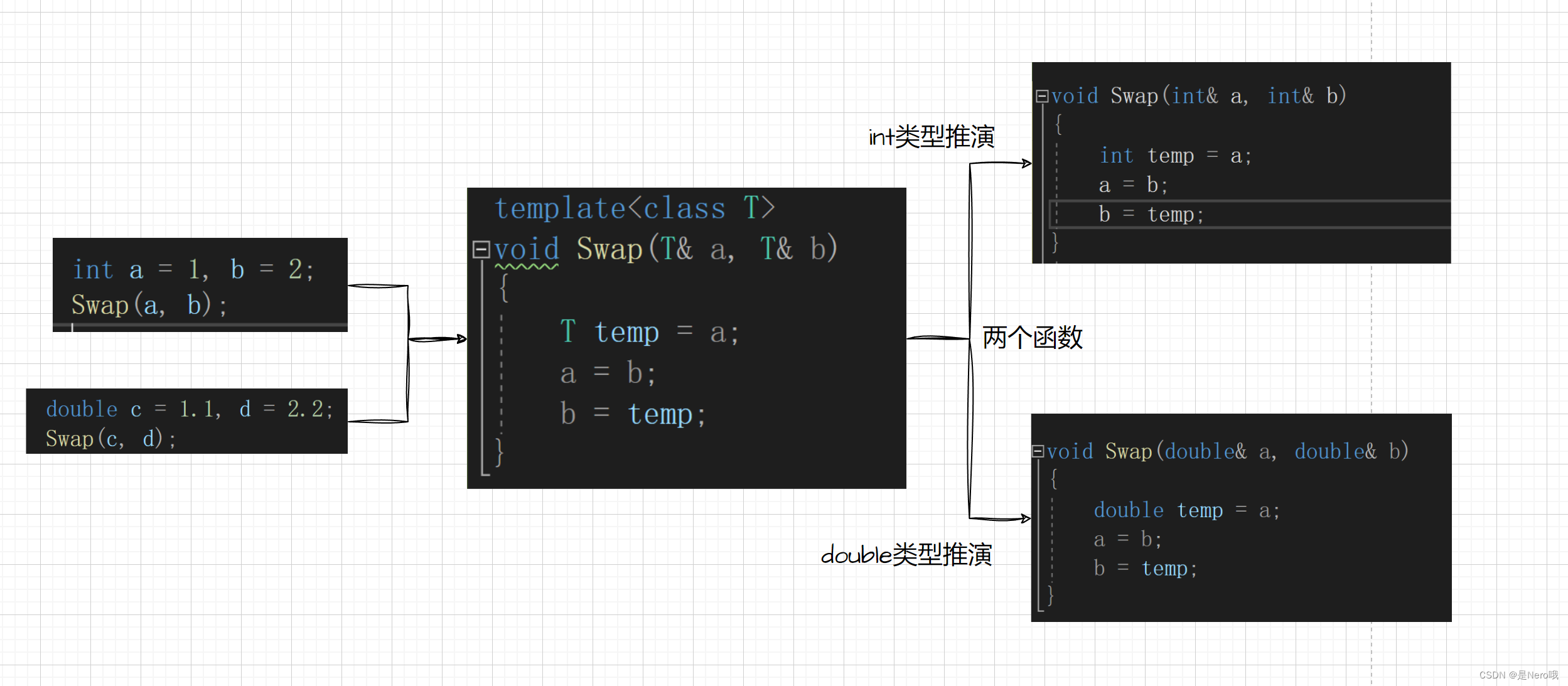
C++初阶:入门泛型编程(函数模板和类模板)
大致介绍了一下C/C内存管理、new与delete后:C初阶:C/C内存管理、new与delete详解 我们接下来终于进入了模版的学习了,今天就先来入门泛型编程 文章目录 1.泛型编程2.函数模版2.1概念2.2格式2.3函数模版的原理2.4函数模版的实例化2.4.1隐式实例…...

【RT-DETR有效改进】CARAFE提高精度的上采样方法(助力细节长点)
👑欢迎大家订阅本专栏,一起学习RT-DETR👑 一、本文介绍 本文给大家带来的CARAFE(Content-Aware ReAssembly of FEatures)是一种用于增强卷积神经网络特征图的上采样方法。其主要旨在改进传统的上采样方法(就是我们的Upsample)的性能。CARAFE的核心思想是:使用输…...
leetcode 27.移除元素(python版)
需求 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出新长度…...

分布式场景怎么Join
背景 最近在阅读查询优化器的论文,发现System R中对于Join操作的定义一般分为了两种,即嵌套循环、排序-合并联接。 考虑到我的领域是在处理分库分表或者其他的分区模式,这让我开始不由得联想我们怎么在分布式场景应用这个Join逻辑ÿ…...
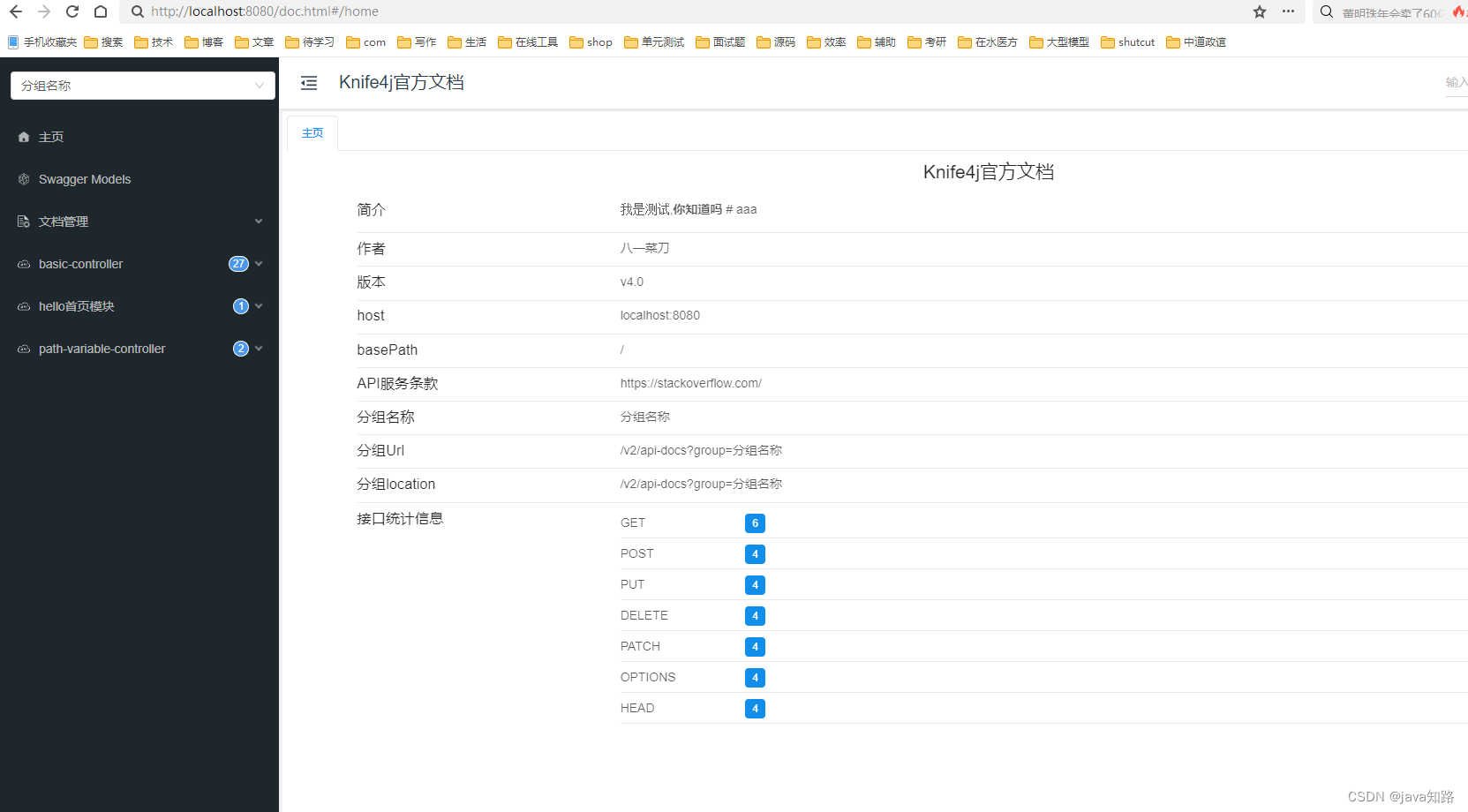
springboot2.7继承swagger knif4j
maven pom依赖 <dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-openapi2-spring-boot-starter</artifactId><version>4.4.0</version></dependency> yml配置 knife4j:enable: trueopenapi:title: …...

C++ 实现单例模式
单例模式 单例模式确保一个类只有一个实例,并提供一个全局访问点。 创建单一实例 怎么让某个类只能创建一个实例? 思路:将类的构造函数私有,然后提供一个静态方法访问对象。调用类内成员函数需要对象,但我们又无法…...
Java多线程--线程安全问题练习题
文章目录 (1)练习题1(2)练习题2(3)练习题3 现在咱们线程一共说了这么几件事情,如下: 具体文章见专栏。 接下来看几个练习题吧。 (1)练习题1 🌋题…...

PHY6252低成本Mesh组网蓝牙芯片
超低成本MESH组网蓝牙芯片PHY6252蓝牙Mesh组网简介 蓝⽛Mesh⽹络使⽤,依赖于低功耗蓝⽛(BLE)。低功耗蓝⽛技术是蓝⽛Mesh使用的无线通信协议栈,蓝牙BR/EDR能够与实现一台设备到另一台设备的连接和通信,建立“一对一”的关系,大多数…...

红外图像中两点校正的增益系数与偏置系数的计算公式推导
增益系数(K) 根据两个温度下的响应值,可求得各响应单元的响应曲线(即斜率),累加所有曲线的斜率求平均斜率值。 平均斜率值与各响应单元的斜率的比值即为该单元的K增益系数。结论:某单元的增益系…...
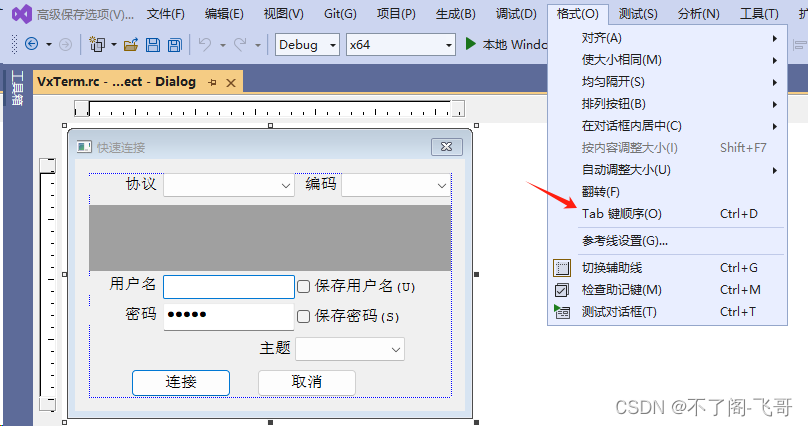
C++/MFC:在窗体Form(Dialog)中多个编辑框时,在输入时将回车解释为TAB键,将输入焦点移到下一个编辑框的方法
很多时候,为了输入方便,常用的做法,就是将回车键解释为将输入焦点移动到下一个编辑框中。就像是我的VxTerm中的快速连接输入一样: VxTerm是一个国产化替代的SSH工具,可以从本站的资源中免费下载并且免费使用ÿ…...

鸿蒙南向开发——GN快速入门指南
运行GN(Generate Ninja) 运行gn,你只需从命令行运行gn,对于大型项目,GN是与源码一起的。 对于Chromium和基于Chromium的项目,有一个在depot_tools中的脚本,它需要加入到你的PATH环境变量中。该脚本将在包含当前目录的…...

PyCharm常用快捷键和设置
Ctrl Space 基本的代码完成(类、方法、属性) Ctrl Alt Space 快速导入任意类 Ctrl Shift Enter 语句完成 Ctrl P 参数信息(在方法中调用参数) Ctrl Q 快速查看文档 F1 外部文档 Shift F1 外部文档…...

Unity - 调节camera物理相机参数(HDRP)
在 “Hierarchy” 右键 -> Volume -> Global Volume new 一个 profile, 设置Mode为Pysical Camera 再点击camera组件,这时候设置 ISO、Shutter Speed、Aperture等参数值还会有效。...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
