订婚支出及共同生活消费是否属于彩礼?应否返还?
恋爱期间,男女双方为增进情感而互赠财物的现象十分普遍。而当双方关系结束时,赠送财物的一方要求对方返还时,法院能否支持其主张?
一起男方向女方及女方母亲索要彩礼及恋爱期间花销钱款引发的婚约财产纠纷案,法院综合双方同居时长、同居消费情况,判令被告赵某返还彩礼钱。。。。。元,对赵某母亲自愿返还的彩礼钱。。。。元予以确认,驳回原告高某其他诉讼请求。
原告高某与被告赵某经媒人介绍后于2023年1月订婚。被告赵某收取了彩礼钱。。。。元及订婚戒指等首饰。后双方共同前往外地工作,并自2023年6月起同居生活。其间,双方因订婚、节日贺礼、医疗、房租等各有支出。2023年8月,双方因琐事发生矛盾,结束同居生活,双方婚礼亦取消。后女方将订婚首饰返还给男方。此后双方因返还彩礼数额等产生纠纷,原告高某将被告赵某及其母亲诉至法院,要求返还全部彩礼以及高某因订婚、准备结婚、恋爱同居期间支出的财物。
法院审理后认为,高某在订婚时给付赵某的彩礼钱。。。。元及首饰,是以缔结婚姻为目的而赠与的价值较大或蕴含结婚意义的财物,视为附解除条件的赠与。现双方已终止恋爱关系,无法实现缔结婚姻目的,赵某收取的彩礼及首饰,考虑到双方存在共同生活的情节,应予适当返还。
恋爱期间,高某为赵某出资购买化妆品、圣诞礼物、旅游消费、节日贺礼、支付医疗费等为增进情感而自愿给付的财物或者赵某为双方共同生活而发生的、未超出日常人情往来范畴的消费性支出或生活开支,应视为一般性赠与,不应予以返还。
对于高某主张订婚产生的布置、花束、酒席、礼品、服装及拍摄婚纱照、房租等支出,系男方为举办订婚仪式或结婚准备、同居生活而支出的各项费用以及高某及其亲友请赵某母亲及其亲友吃饭的费用等,以上均非对女方个人的赠与,也不属于彩礼范畴,要求返还于法无据。法院遂作出上述判决。
■法官说法
恋爱期间,情侣相互赠送财物,受赠人表示接受的行为,根据《中华人民共和国民法典》第六百五十七条的规定,双方成立赠与合同。在对恋爱期间财物来往关系性质进行判定时,主要取决于双方当时的意思表示,通过往来金额的大小、用途及各方经济能力等事实因素进行判定。一般赠与情况下,财产一旦交付或者转移登记,赠与合同即生效,在无法定撤销权事由情形下,一般不能要求受赠人返还。彩礼相较于一般赠与,赠与的金额超出表达爱意、增进情感一般性赠与金额的范畴,属于非生活必须消费且金额较大,且以结婚为目的,具有较强的人身属性,实际上在赠与合同上附加了解除条件,一旦双方无法缔结婚姻,受赠人应返还受赠的财物。至于具体金额,可以结合双方是否共同生活、生活时间长短、彩礼的使用情况、双方是否存在过错及给付一方家庭经济状况等因素进行综合考量。
相关文章:

订婚支出及共同生活消费是否属于彩礼?应否返还?
恋爱期间,男女双方为增进情感而互赠财物的现象十分普遍。而当双方关系结束时,赠送财物的一方要求对方返还时,法院能否支持其主张? 一起男方向女方及女方母亲索要彩礼及恋爱期间花销钱款引发的婚约财产纠纷案,法院综合双…...

MicroPython核心:优化
MicroPython使用多种优化方法来节省RAM,同时确保程序的高效执行,本文会讨论其中的一些优化。 提示: MicroPython 字符串驻留(string interning) 和映射和字典(Maps and Dictionaries) 详细介绍了对字符串和字典的其他…...
Opencv——霍夫变换
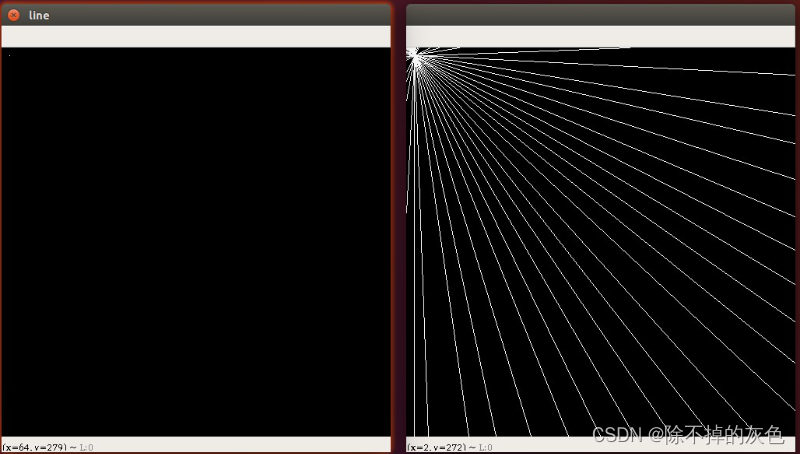
霍夫直线变换 霍夫直线变换(Hough Line Transform)用来做直线检测 为了加升大家对霍夫直线的理解,我在左图左上角大了一个点,然后在右图中绘制出来经过这点可能的所有直线 绘制经过某点的所有直线的示例代码如下,这个代码可以直接拷贝运行 import cv2 as cv import matplot…...

Github 2024-01-28 开源项目日报Top10
根据Github Trendings的统计,今日(2024-01-28统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目3TypeScript项目2Rust项目1HTML项目1JavaScript项目1Cuda项目1C#项目1非开发语言项目1 Nuxt&#…...
【大数据安全】大数据安全的挑战与对策基础设施安全
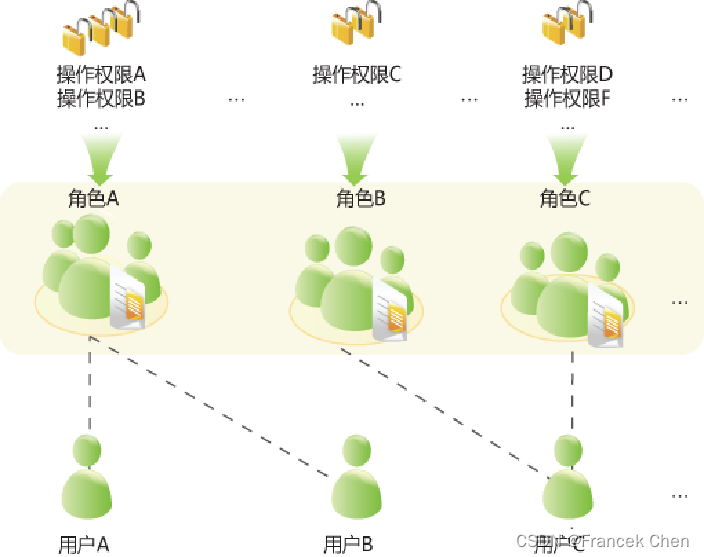
目录 一、大数据安全的挑战与对策 (一)数据加密技术 (二)大数据安全与隐私 (三)大数据安全保障体系 (四)华为大数据安全解决方案 二、基础设施安全 (一࿰…...
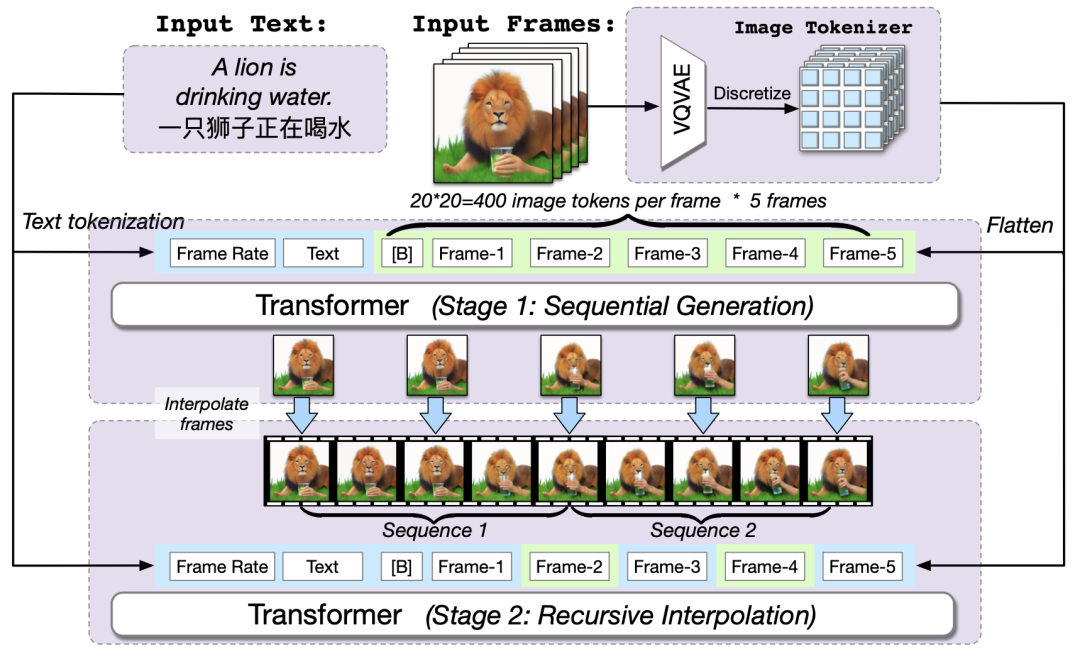
【LLM多模态】Cogview3、DALL-E3、CogVLM、CogVideo模型
note 文章目录 noteVisualGLM-6B模型图生文:CogVLM-17B模型1. 模型架构2. 模型效果 文生图:CogView3模型DALL-E3模型CogVideo模型网易伏羲-丹青模型Reference VisualGLM-6B模型 VisualGLM 是一个依赖于具体语言模型的多模态模型,而CogVLM则是…...

python爬虫学习之selenium_chrome handless的使用
目录 一、Chrome handless简介 二、Chrome handless的系统要求 三、Chrome handless的基本配置 (直接复制放在.py文件开头) 四、Chrome handless 的应用 五、Chrome handless的封装 一、Chrome handless简介 Chrome handless 模式,Goog…...
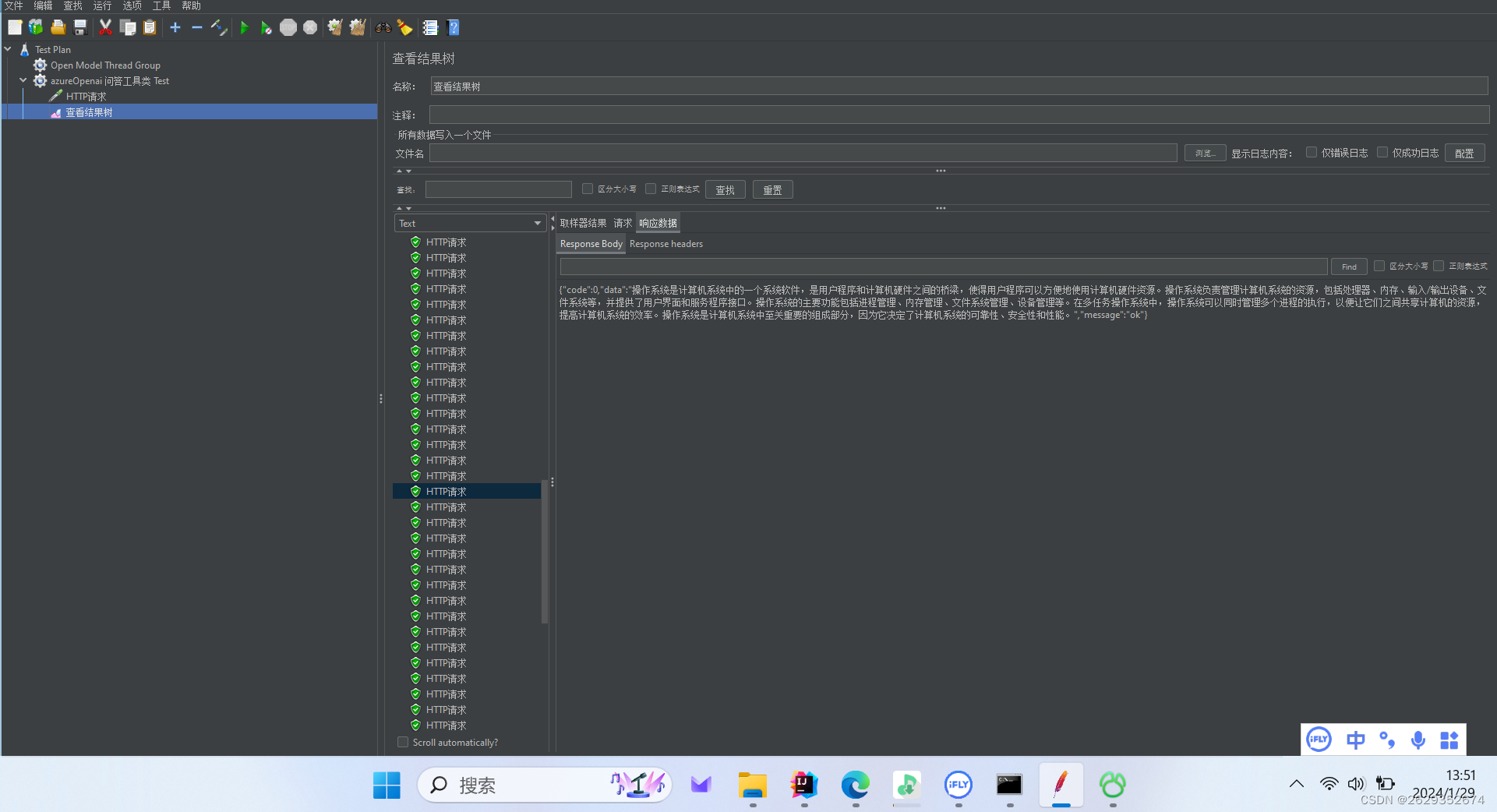
Spring boot + Azure OpenAI 服务 1.使用 GPT-35-Turbo
Azure OpenAI 服务使用 GPT-35-Turbo 先决条件 maven 注意 beta.6 版本 <dependency><groupId>com.azure</groupId><artifactId>azure-ai-openai</artifactId><version>1.0.0-beta.6</version></dependency>问答工具类 pack…...
Vite+Vue3使用Vue-i18n笔记
一、下载依赖 vue-i18n yarn add vue-i18n创建存放语言文件的目录 以及配置文件的配置 我是在src/lang 新建index.ts、cn.ts、en.ts以及test文件夹其中再分别新建cn.ts以及en.ts /lang/index.ts 用于导出vue-i18n需要的配置对象 import en from "./en.ts"; import…...

流量密码《幻兽帕鲁》5天狂销700万份
*** 流量密码《幻兽帕鲁》5天狂销700万份 2024年,一匹游戏业的黑马没有预兆地就这么出现了 这就是《幻兽帕鲁》 它首日销量轻松达到200万,5天时间手到擒来700万销量,直接收入超15亿,刷新多个游戏市场纪录。 同时在线玩家数高达…...
怎么查询鸿蒙真机支持的API版本
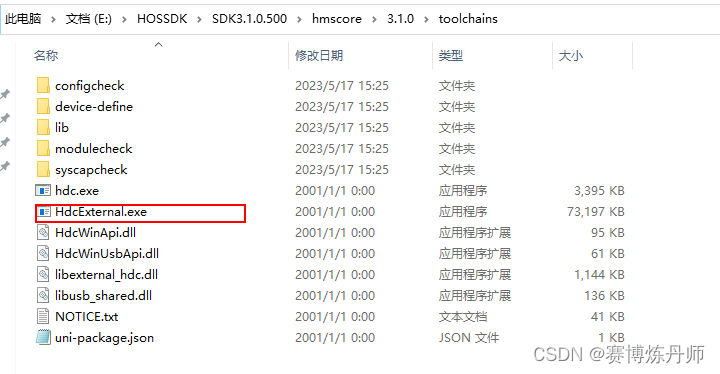
1、打开设备的开发者模式与USB调试并通过USB连接上电脑。 2、管理员身份运行cmd。 3、进入hdc.exe所在目录。(鸿蒙OS IDE的SDK下载目录中) 4、输入hdc shell,进入特殊模式 5、输入 getprop hw_sc.build.os.apiversion 查看API版本 6、输入 getprop hw_sc.build…...

【NodeJS】005- NodeJS的NVM与express框架
1.NVM介绍与使用 1.介绍 nvm 全称 Node Version Manager 顾名思义它是用来管理 node 版本的工具,方便切换不同版本的Node.js 2.使用 nvm 的使用非常的简单,跟 npm 的使用方法类似 3.下载安装 首先先下载 nvm,下载地址 https://github.com/coreybutler/nvm-windows/rel…...

pandas使用read_csv时报错解决
问题描述: 在使用read_csv时报错: UnicodeDecodeError: utf-8 codec cant decode byte 0xc9 in position 9451: invalid continuation byte 或者: UnicodeDecodeError: gb2312 codec cant decode byte 0x88 in position 68296: illegal m…...
Optimism的挑战期
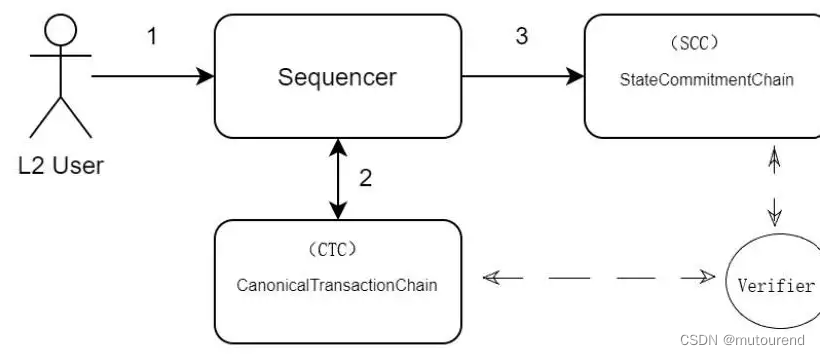
1. 引言 前序博客: Optimism的Fault proof 用户将资产从OP主网转移到以太坊主网时需要等待一周的时间。这段时间称为挑战期,有助于保护 OP 主网上存储的资产。 而OP测试网的挑战期仅为60秒,以简化开发过程。 2. OP与L1数据交互 L1…...

Linux——安装MySQL
1、安装mysql8.0.35 1.1、安装步骤 1.更新包列表,首先,确保您的系统已更新到最新状态。运行以下命令来更新包列表和安装最新的软件包: sudo apt update sudo apt upgrade2.安装MySQL服务器:运行以下命令来安装MySQL服务器&…...
java常量和kotlin常量
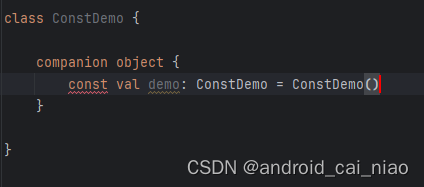
在java中使用final声明常量在kotlin中使用const val声明常量 常量在编译为字节码后会直接把调用常量的地方直接替换为常量值,示例如下: public class ConstDemo {public static final String NAME "Even";private static final int ID 100…...

Python学习笔记--创建最简单的自定义异常类
在Python中,当创建一个函数时,它应该执行一些操作或返回一些值。如果函数为空,则没有实际的操作或返回值,这是不符合函数设计的初衷的。因此,在Python中,函数体不能为空,必须至少包含一个语句&a…...
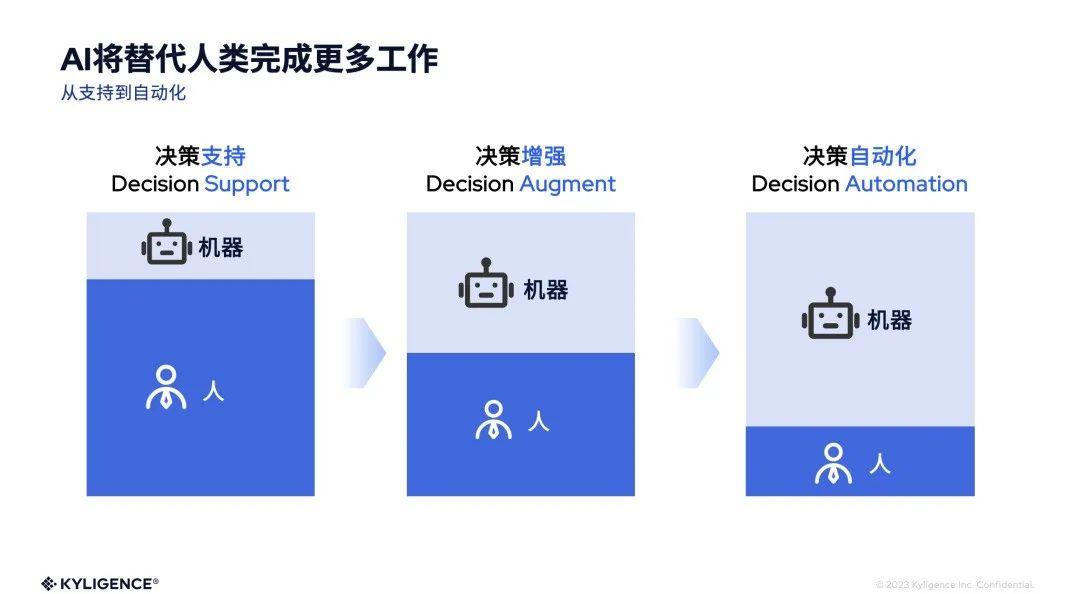
2024年,AI 掀起数据与分析市场的新风暴
2024 年伊始,Kyligence 联合创始人兼 CEO 韩卿在其公司内部的飞书订阅号发表了多篇 Rethink Data & Analytics 的内部信,分享了对数据与分析行业的一些战略思考,尤其是 AI 带来的各种变化和革命,是如何深刻地影响这个行业乃至…...

小程序软件测试应该怎么做?有什么作用?
近年来,随着移动互联网的快速发展,小程序软件的使用越来越广泛。无论是企业推广还是个人创作,小程序软件都具备了很大的潜力和市场空间。然而,在发布之前,进行充分的测试是至关重要的,以确保用户体验的顺畅…...

springboot2.2.9整合kafka之KafkaListener实现原理
1、开启kafka的注解EnableKafka 通过开启kafka注解可以看到Import的类KafkaListenerConfigurationSelector加载一个配置类KafkaBootstrapConfiguration,而此类中有两个重要的类: KafkaListenerAnnotationBeanPostProcessor、KafkaListenerEndpointRegistry 2、Kaf…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
