图的学习
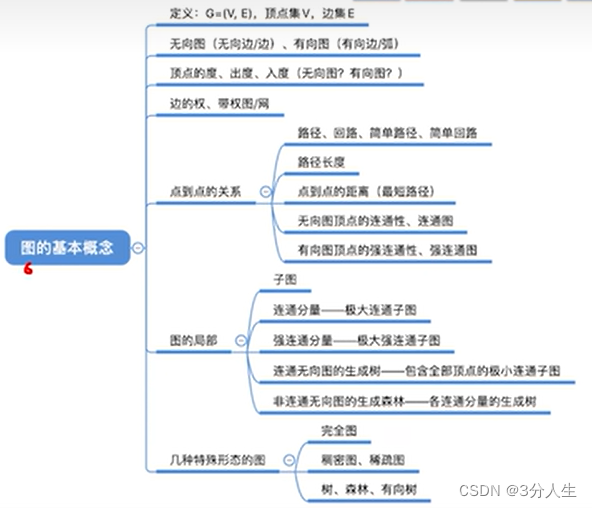
图的基本概念和术语
图的定义:图是由顶点的有穷非空集合和顶点之间的边的集合组成的,G表示,V是图G中顶点的集合,E是图G中边的集合
无向图:任意两点的边都是无向边组成的图(无向边:(A,B)表示点A能到点B,点B也能到点A)
有向图:任意两点的弧都是有向边组成的图(有向边:<A,B>表示点A能到点B,点B不能到点A(B为弧头,A为弧尾)
边较少的图叫稀疏图,反之叫稠密图
权,网:图的边或弧相关的数叫权,这种带权的图通常叫做网
顶点的度:无向图中顶点的度表示和顶点相关联的的边的数目(记TD);有向图中分为入度和出度
入度为顶点为弧头有关联的弧,出度为顶点为弧尾有关联的弧
路径长度:路径长度是路径上边或弧的数目
回路,环:第一个顶点和最后一个顶点相同的路径称为回路或环
连通图:图中任意两点都是连接的(有路径),有向图中称为强连通图
无向图中联通n个顶点和n-1条边叫生成树,有向图中一顶点入度为0其余顶点入度为1的叫有向树。

图的储存结构
邻接矩阵
图的邻接矩阵采用顺序存储结构,用一个一维数组储存顶点的信息,一个二维数组储存图中边或弧的的信息

优点:便于理解,适合稠密图,O(1)判断两点是否有边,删除边比较方便
缺点:遇到边较少的图,浪费大量空间,图的建立,dfs,bfs遍历时间复杂度较高为O(N^2),删除点不方便
邻接表
邻接表采用顺序+链式存储结构,一个一维结构体数组(数组大小为结点数量),结构体数组的存储元素构成单链表,每一个单链表链接与该结点相连的点

优点:根据需求分配空间,浪费的空间较少,适合稀疏图
缺点:删除边或点比较麻烦,对于有向图不利于求某个点出度的数量

图的遍历
广度优先遍历和深度优先遍历,对于邻接矩阵和邻接表的时间复杂度都为平方阶和线性阶
所以对于有关于图的遍历问题一般采用邻接表储存图,时间开销更小
图中如果不是联通图,存在一次遍历不能遍历全部的点,一般用数组标记判断点是否遍历
模板题 洛谷 P5318 查找文献
本题考察图的深度和广度
题目描述
小 K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个(也有可能没有)参考文献的链接指向别的博客文章。小 K 求知欲旺盛,如果他看了某篇文章,那么他一定会去看这篇文章的参考文献(如果他之前已经看过这篇参考文献的话就不用再看它了)。
假设洛谷博客里面一共有n(n≤10^5) 篇文章(编号为 1 到 n)以及 m(m≤10^6) 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章,请帮助小 K 设计一种方法,使小 K 可以不重复、不遗漏的看完所有他能看到的文章。
这边是已经整理好的参考文献关系图,其中,文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。
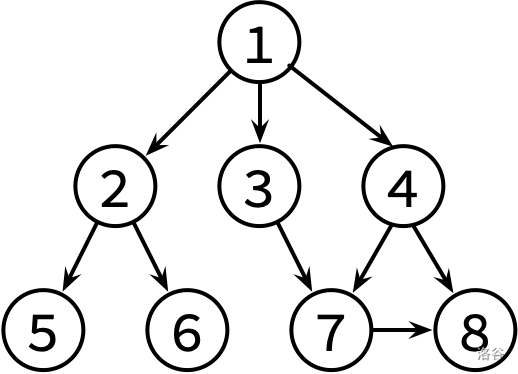
请对这个图分别进行 DFS 和 BFS,并输出遍历结果。如果有很多篇文章可以参阅,请先看编号较小的那篇(因此你可能需要先排序)。
输入格式
共 m+1 行,第 1 行为 2 个数,n 和 m,分别表示一共有 n(n≤10^5) 篇文章(编号为 1 到 n)以及m(m≤10^6) 条参考文献引用关系。
接下来 m 行,每行有两个整数 X,Y 表示文章 X 有参考文献 Y。
输出格式
共 2 行。 第一行为 DFS 遍历结果,第二行为 BFS 遍历结果。
输入输出样例
输入 #1
8 9 1 2 1 3 1 4 2 5 2 6 3 7 4 7 4 8 7 8
输出 #1
1 2 5 6 3 7 8 4 1 2 3 4 5 6 7 8
看题发现本题的n的范围10^5用邻接矩阵不仅空间存不下,遍历也浪费时间,所以采用邻接表
这题不需要考虑是否为连通图,题目的数据,若是存在一个点与1号点没有联系则不需要输出这个点
思路
我们知道邻接表遍历结果不唯一的,而题目要求请先看编号较小的那篇(因此你可能需要先排序),链表不好进行排序,我们可以先对输入的m个x和y进行排序,因为对于邻接表一般采用头插法(先插入的点在链表的最后),按照y的比较进行降序排列,这样可以保证每一个单链表都是升序。
AC代码
#include<stdio.h>
#include<stdlib.h>
struct nb {int data;struct nb* p;
}a[100010];//邻接表
struct mm {int l, r;
}mr[1000010], b[1000010];//b为归并辅助数组
void guibin(int x, int y)//归并排序不多说
{if (x >= y) return;long long mid = (x + y) / 2, i, j;guibin(x, mid);guibin(mid + 1, y);int cnt = 0;for (i = x, j = mid + 1; i <= mid && j <= y;){if (mr[i].r >= mr[j].r)b[++cnt] = mr[i++];elseb[++cnt] = mr[j++];}while (i <= mid)b[++cnt] = mr[i++];while (j <= y)b[++cnt] = mr[j++];for (i = 1; i <= cnt; i++)mr[x + i - 1] = b[i];
}
int book[100010], book1[100010] = { 0 };//标记数组
void dfs(int x)
{struct nb* gg;book[x] = 1;//第一次访问标记为1printf("%d ", x);//打印结果gg = a[x].p;while (gg){if (book[gg->data] == 0)//第一次访问dfs搜索dfs(gg->data);gg = gg->p;}
}
void bfs(int x)
{int link[100010];int hard = 1, tail = 2;link[1] = x; book1[x] = 1;while (hard < tail){printf("%d ", link[hard]);struct nb* f = a[link[hard]].p;while (f != NULL){if (book1[f->data] == 0){link[tail++] = f->data;book1[f->data] = 1;}f = f->p;}hard++;}
}
int main()
{int n, m, i, j;struct nb* q, * t, * s;scanf("%d %d", &n, &m);for (i = 1; i <= m; i++)//输入m个x,yscanf("%d %d", &mr[i].l, &mr[i].r);for (i = 1; i <= n; i++)a[i].p = NULL;guibin(1, m);//降序排序for (i = 1; i <= m; i++)//邻接表的建立{q = (struct nb*)malloc(sizeof(struct nb));q->data = mr[i].r; q->p = a[mr[i].l].p;a[mr[i].l].p = q;}dfs(1);//dfs搜索printf("\n");bfs(1);//bfs搜索for (i = 1; i <= n; i++)//清空邻接表链表,避免内存泄露{s = a[i].p;while (s != NULL){t = s;s = s->p;free(t);}}return 0;
}
相关文章:

图的学习
图的基本概念和术语 图的定义:图是由顶点的有穷非空集合和顶点之间的边的集合组成的,G表示,V是图G中顶点的集合,E是图G中边的集合 无向图:任意两点的边都是无向边组成的图(无向边:(…...

空间数据分析入门POI与莫兰指数基础知识笔记
1. 空间分析与POI 1.1. 什么是POI POI是“Polnt of Information”的缩写,中文可以翻译为“信息点”。POI是地图上任何非地理意义的有意义的点,如商店、酒吧、加油站、医院、车站等。这些点通常包括名称、类别、经纬度和地址等基本信息。此外࿰…...
TortoiseSVN各版本汉化包下载
首先进入下载版本列表 1.下载地址:https://sourceforge.net/projects/tortoisesvn/files 2.选择自己版本进入 3.选择Language Packs进入,选择对应语言包下载。 4.在TortoiseSVN根目录下点击安装即可。 ...
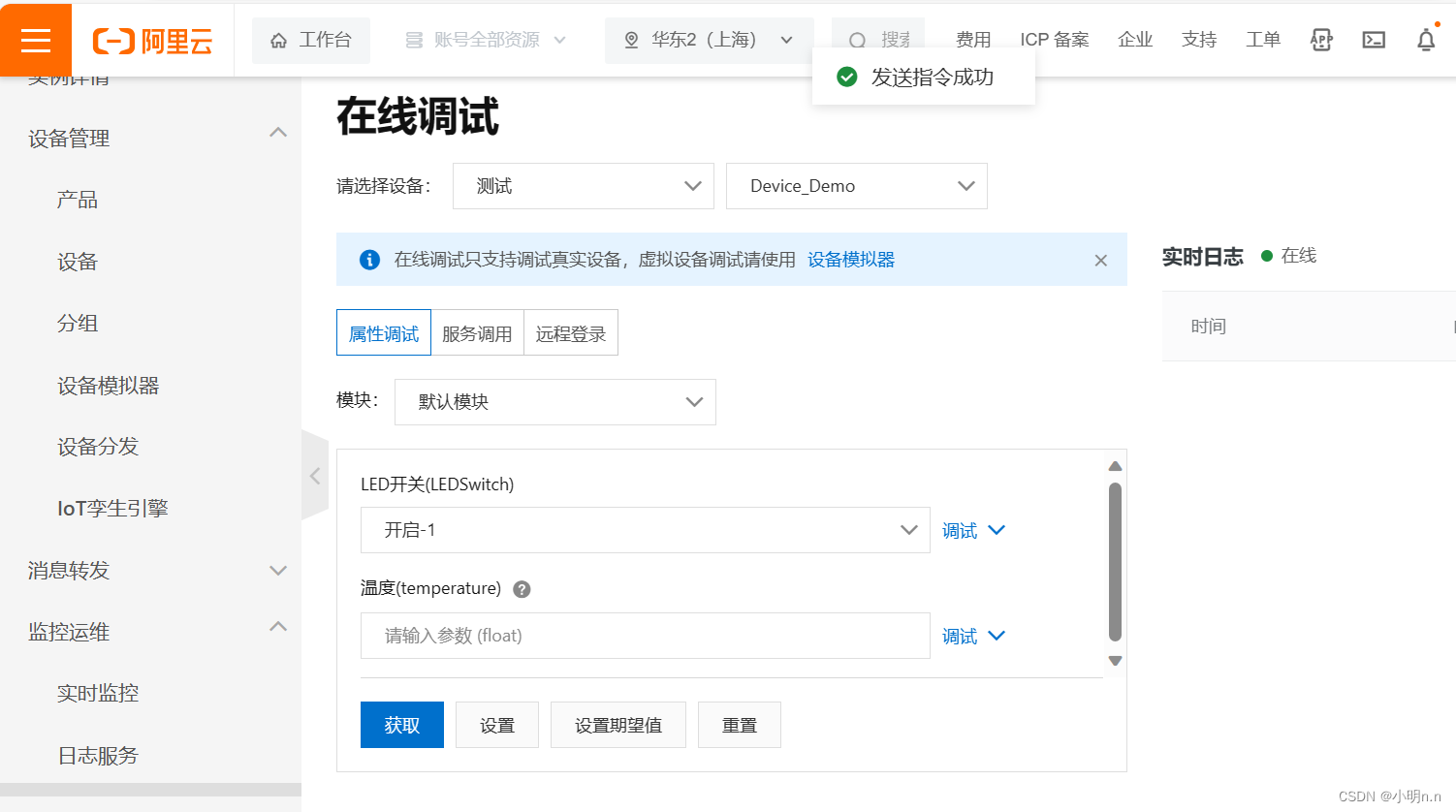
STM32连接阿里云物联网平台
文章目录 引言一、STM32连接阿里云物联网平台思路二、ESP8266烧录固件三、使用AT指令连接阿里云物联网平台四、STM32环形串口缓冲区驱动程序五、STM32连接阿里云驱动程序 引言 连续写了两篇关于阿里云连接的文章,都是使用Arduino ESP8266 & Arduino ESP32的方式…...
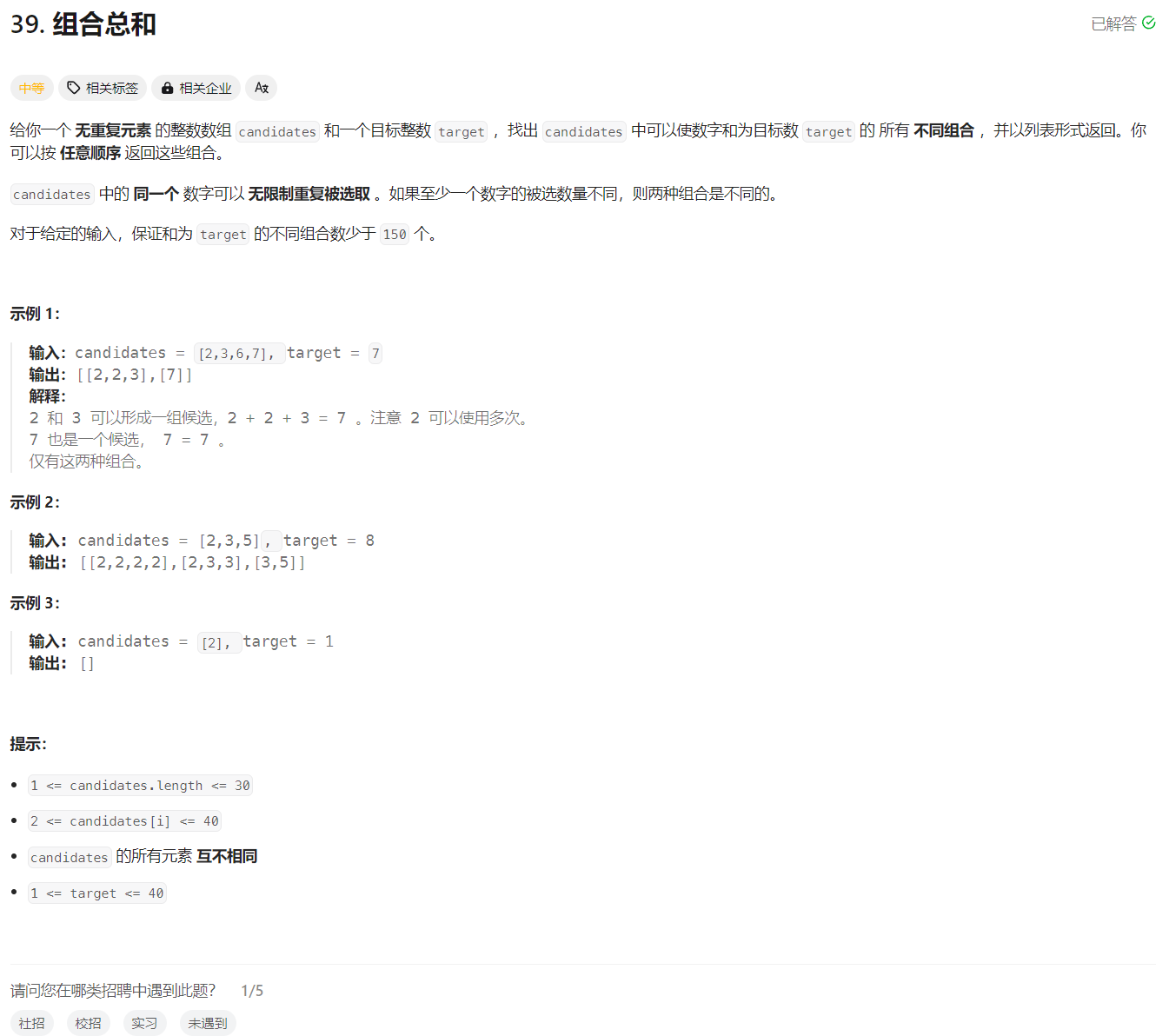
力扣hot100 组合总和 回溯 剪枝 组合
Problem: 39. 组合总和 文章目录 思路复杂度💖 Code 思路 复杂度 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( n ) O(n) O(n) 💖 Code class Solution{List<List<Integer>> res new ArrayList<>();int x;// 全局targetin…...
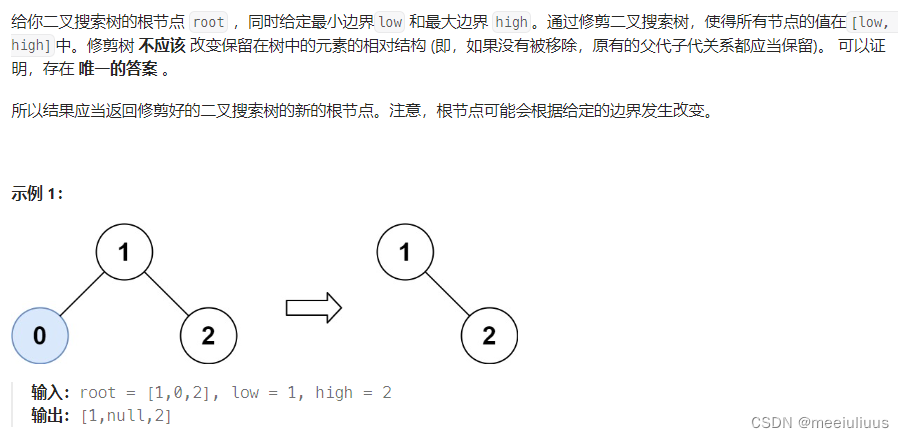
代码随想录 Leetcode669. 修剪二叉搜索树
题目: 代码(首刷看解析 2024年1月31日): class Solution { public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (!root) return root;if (root->val < low) {TreeNode* node trimBST(root->right,low,high);return…...
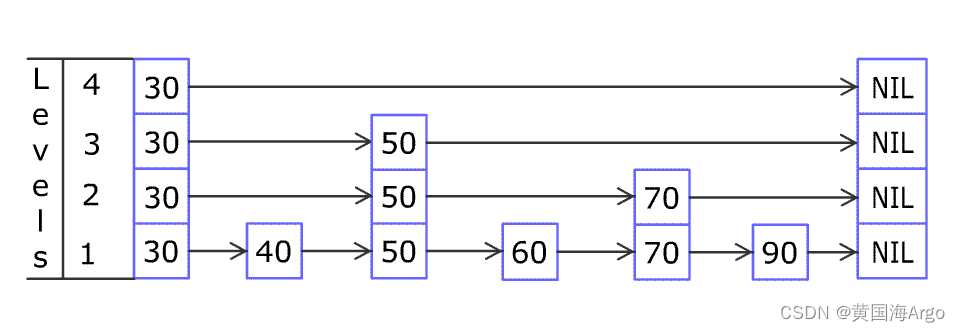
Redis系列-数据结构篇
数据结构 string(字符串) redis的字符串是动态字符串,类似于ArrayList,采用预分配冗余空间的方式减少内存的频繁分配。 struct SDS<T>{ T capacity; T len; byte flags; byte[] content; } 当字符串比较短时,…...
正则表达式(RE)
什么是正则表达式 正则表达式,又称规则表达式(Regular Expression)。正则表达式通常被用来检索、替换那些符合某个规则的文本 正则表达式的作用 验证数据的有效性替换文本内容从字符串中提取子字符串 匹配单个字符 字符功能.匹配任意1个…...

发布技术路线图!美国量子计算公司QuEra公开三年OKR
编辑丨慕一 编译/排版丨琳梦 卉可 深度好文:1100字丨8分钟阅读 近期,美国量子计算公司QuEra Computing宣布了一系列关于容错量子计算机的战略路线图,该路线图从2024年开始,最终目标是打造具有100纠错逻辑量子比特的系统。 在…...

Vue2:请求接口的两种方式axios和vue-resource
一、场景描述 前端和后端的交互,肯定是要发生接口调用的 这个时候,就要涉及前端如何向后端接口发送请求,获取数据 二、请求方式 1、axios方式(推荐) 这个方式本质就是ajax,底层就是对xhr(XMLHttpRequest)的封装 1、安装axios…...
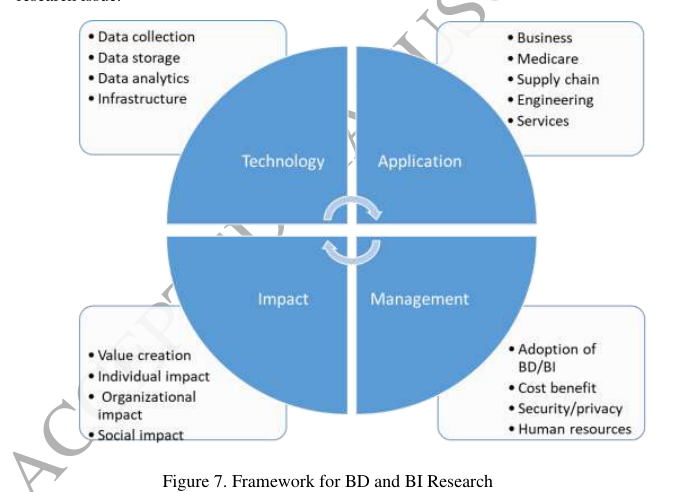
扩展学习|商业智能和大数据分析的研究前景(比对分析)
文献来源: Liang T P , Liu Y H .Research Landscape of Business Intelligence and Big Data analytics: A bibliometrics study[J].Expert Systems with Applications, 2018, 111(NOV.):2-10.DOI:10.1016/j.eswa.2018.05.018. 信息和通信技术的快速发展导致了数字…...

『Docker入门指南』- 详细安装与配置教程,助你起航容器化世界!
引言 在探索云计算和自动化部署的时代,Docker以其独特的容器化技术站在了风口浪尖。如果你期待着无缝地将你的应用从一个环境迁移到另一个环境,那么Docker无疑是你的得力助手。但首先,我们得学会如何正确地安装和配置Docker。这篇文章将详细…...

如何提高http连接成功率?
问题 丢包、错包、乱包 高延迟 响应数据回来时间长,甚至大于客户端等待时间 带宽小 每次能够通信的内容较少,数据包越大受影响可能越大 网络断续 网络经常断开又连接 优化处理 采用TCP协议、实现长连接,采用长连接池,节省…...

Elasticsearch 中使用MustNot等同于不等于遇到的坑
1、在写关键词推荐时,需要把当前文章过滤掉,不能再推荐自己的文章,所以再es中需要用到 MustNot属性查询 /// <summary> /// 服务中心es检索 /// </summary> /// <param name="input"></param> /// <returns></…...

嵌入式工程师day15(链表)
内存管理 一.内存管理: 1.malloc void *malloc(size_t size); 功能: 申请堆区空间 参数: size:申请堆区空间的大小 返回值: 返回获得的空间的首地址 失败返回NULL 2.free void free(void *ptr); 功能: 释放…...
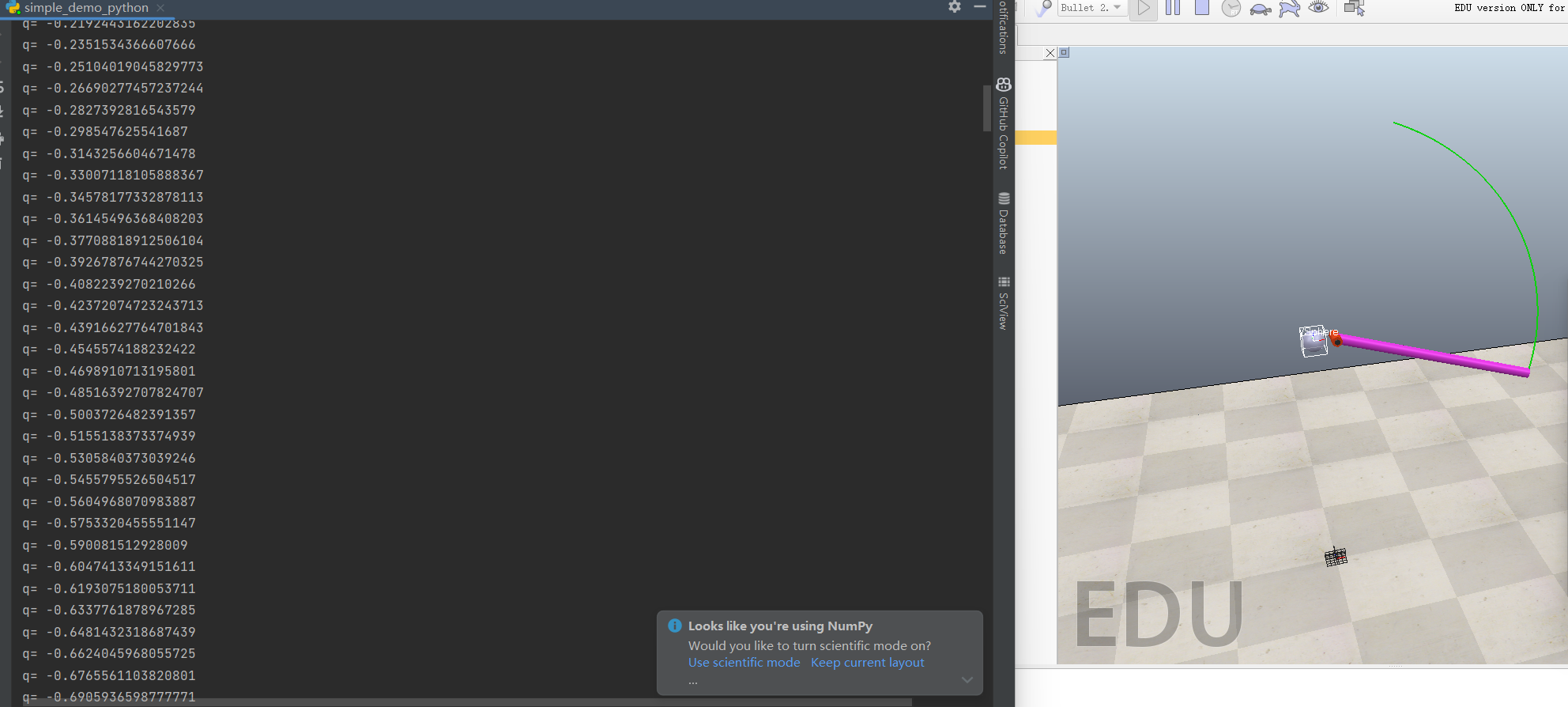
Coppeliasim倒立摆demo
首先需要将使用Python远程控制的文件导入到文件夹,核心是深蓝色的三个文件。 本版本为4.70,其文件所在位置如下图所示,需要注意的是,目前不支持Ubuntu22的远程api: 双击Sphere这一行的灰色文件,可以看到远程…...

汽车燃油泵数据分析:全球市场的年复合增长率将达到10%左右
燃油泵是汽车配件行业的专业术语。是电喷汽车燃油喷射系统的基本组成之一,位于车辆油箱内部,燃油泵在启动和发动机运转时工作,如果发动机停止而点火开关仍处于ON时,HFM-SFI控制模块关闭燃油泵的电源,以避免意外点火。 …...
)
DC-磁盘管理(23国赛真题)
2023全国职业院校技能大赛网络系统管理赛项–模块B:服务部署(WindowServer2022) 文章目录 题目配置步骤组成RAID 5,磁盘分区命名为卷标H盘:Raid5。手动测试破坏一块磁盘,做RAID磁盘修复,确认RAID 5配置完毕。验证查看Raid5(打开磁盘管理器,查看raid信息)Raid5磁盘修复…...
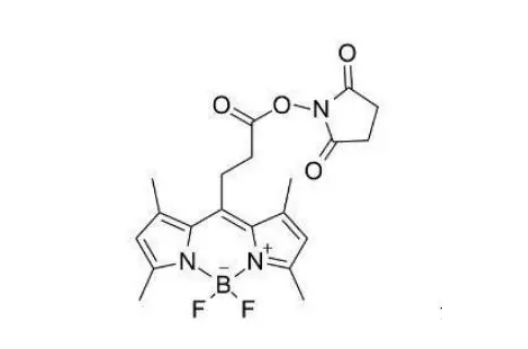
216961-98-7,BODIPY 493/503 NHS 活化酯,可以应用于分子生物学等领域中
您好,欢迎来到新研之家 文章关键词:216961-98-7,BODIPY 493/503 NHS 活化酯,BODIPY 493/503 NHS ester,BODIPY 493/503 SE 一、基本信息 产品简介:BODIPY 493/503 NHS ester是一种特殊的染料,…...

Python采集学习笔记-读取excel数据
表格格式 方法一:使用xlrd import xlrd 1.读取Excel文件 workbook xlrd.open_workbook(plc.xlsx) 2.读取第一个表 sheet workbook.sheet_by_index(0) 3.获取表格总行数 total_rows sheet.nrows 4.创建列表,存储表格一行中每一列信息 plc_info [] for row in range(1…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
