[经典面试题]169. 多数元素
题目描述
给定一个大小为
n的数组nums,返回其中的多数元素。多数元素是指在数组中出现次数 大于⌊ n/2 ⌋的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3] 输出:3示例 2:
输入:nums = [2,2,1,1,1,2,2] 输出:2
解题方法分析:
使用哈希算法(HashMap)来存储每个元素以及出现的次数。通过求解哈希映射中的每个键值对,键表示一个元素,值表示该元素出现的次数,统计出数组出现的数字次数最多的那一过。
首先循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后,我们遍历哈希映射中的所有键值对,返回值最大的键,这样就可以通过哈希统计出出现次数最多的数字。
代码:
class Solution {
public:int majorityElement(vector<int>& nums) {// 使用map来记录每个数字的出现次数std::map<int, int> counts;// majority用于记录当前的多数元素,cnt用于记录多数元素出现的次数int majority = 0, cnt = 0;// 遍历输入数组for (int num : nums) {// 将当前数字的出现次数加一++counts[num];// 如果当前数字的出现次数超过之前记录的多数元素的次数if (counts[num] > cnt) {// 更新多数元素和出现次数majority = num;cnt = counts[num];}}// 返回最终找到的多数元素return majority;}
};相关文章:

[经典面试题]169. 多数元素
题目描述 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出:3…...
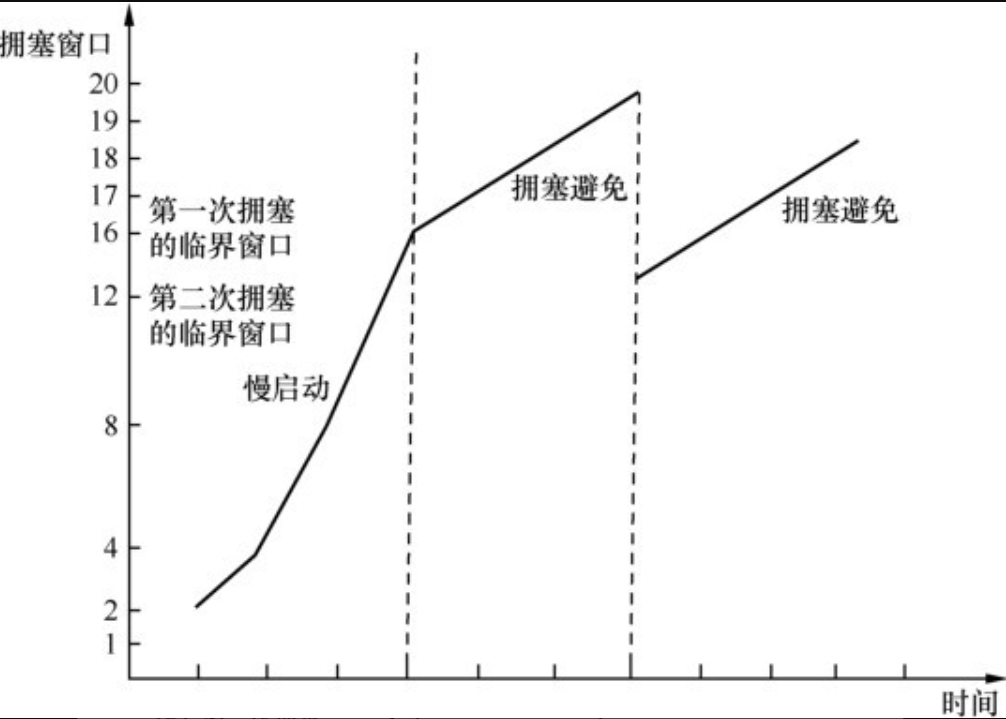
Wireshark网络协议分析 - TCP协议
在我的博客阅读本文 文章目录 1. 基础2. 实战2.1. 用Go写一个简单的TCP服务器与客户端2.2. Wireshark抓包分析2.3. 限制数据包的大小——MSS与MTU2.4. 保证TCP的有序传输——Seq,Len与Ack2.5. TCP头标志位——URG,ACK,PSH,RST&…...
3 款最好的电脑硬盘数据迁移软件
您将从本页了解 3 款最好的 SSD硬盘数据迁移软件,磁盘供应商提供的软件和可靠的第三方软件。仔细阅读本文并做出您的选择。 什么是数据迁移? 数据迁移是将数据移动到其他计算机或存储设备的过程。在日常工作活动中,常见的数据迁移有三种&…...

【Java之HTML】
HTML 概念 互联网的产生:w3c的成立, 互联网最开始设计的目的:看论文 ---->浏览器,HTML 网络三要素:HTML HTTP URL HTML描述论文的格式 HTTP标记这个论文在网络上怎么传输 URL:指示这个论文在互联网的哪…...

支付宝支付功能解析,从零到掌握,轻松享受便捷支付
目录 一、支付宝支付功能简介 1.1 支付宝支付的概念 1.2 支付宝支付的优势 1.3 支付宝支付的适用场景 二、支付宝支付的准备工作 三、支付宝支付的接入流程 四、支付宝支付的安全性 5.1 支付宝支付的安全机制 5.2 防范支付风险的措施 5.3 支付宝支付的安全技术保障 …...
MacOS安装反编译工具JD-GUI以及解决无法打开的问题
目录 一.下载地址 二.安装 三.问题 四.解决办法 1.显示包内容 2.找到Contents/MacOS/universalJavaApplicationStub.sh 3.修改sh文件 4.保存后再次打开即可 一.下载地址 Java Decompiler 二.安装 将下载下来的 jd-gui-osx-1.6.6.tar 解压,然后将 JD-GUI.a…...
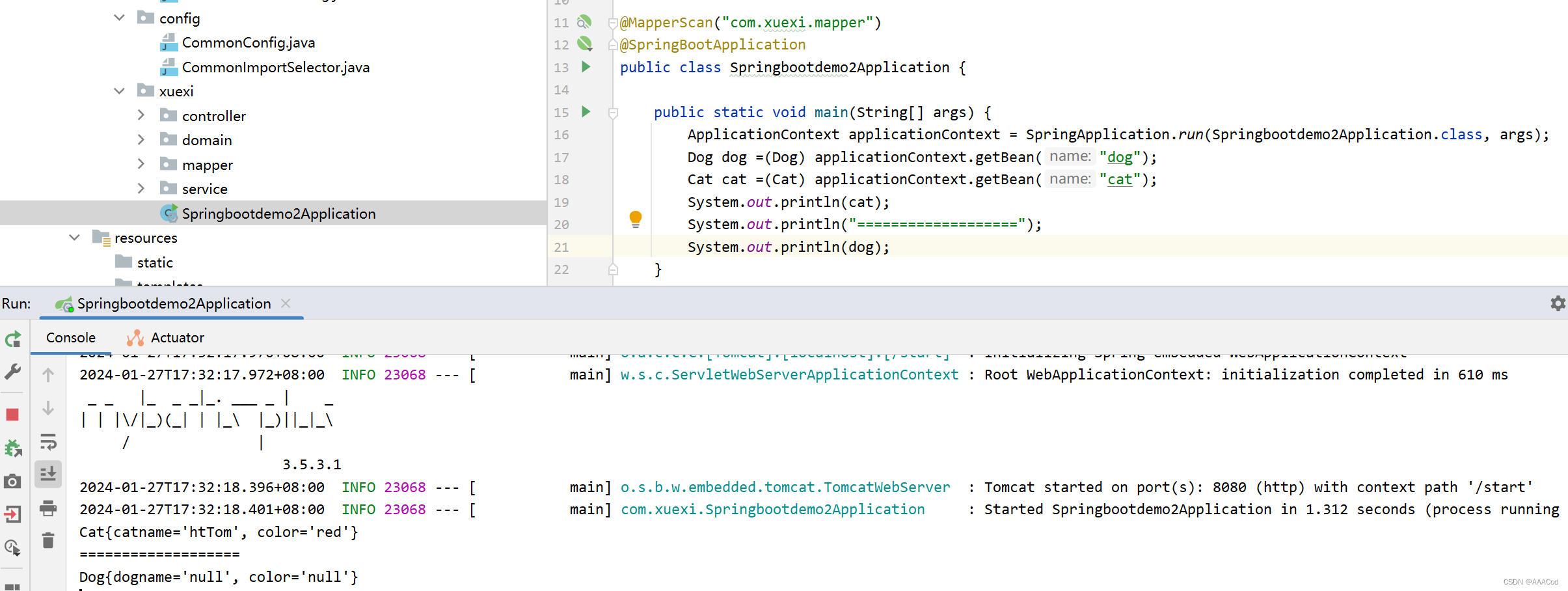
SpringBoot将第三方的jar中的bean对象自动注入到ioc容器中
新建一个模块,做自动配置 config:需要准备两个类,一个自动配置类,一个配置类 CommonAutoConfig:此类用于做自动配置类它会去读取resoutces下的META-INF.spring下的org.springframework.boot.autoconfigure.AutoConfig…...

5.变量的解构赋值 - JS
什么是解构赋值 通过类似(或相同)的构型,将已知数据的元素/属性解构并提取出来,再赋值到相应变量,可以是新建的变量,也可以是已存在的变量/属性等;最常见的是数组和对象的解构赋值,…...
tableau添加形状
目录 1.效果:1.自带的形状:2.添加形状:小结: 1.效果: 1.自带的形状: 2.添加形状: 找到tableau的安装目录,点入 默认->形状 的文件夹: 新建一个文件夹: …...

(2)(2.10) LTM telemetry
文章目录 前言 1 协议概述 2 配置 3 带FPV视频发射器的使用示例 4 使用TCM3105的FSK调制解调器示例 前言 轻量级 TeleMetry 协议 (LTM) 是一种单向通信协议(从飞行器下行的数据链路),可让你以低带宽/低波特率(通常为 2400 波…...
)
工具推荐系列-极客编辑器(实时在线编写md文件同步GitHub)
工具项目地址:https://github.com/geekeditor/geekeditor-desktop-releases/tree/main 工具基础配置方法:https://www.geekeditor.com/workspace1.x.html 详细同步代码仓的方法可以用下面: 如何创建GitHub仓库 及生成获取AccessToken…...

3d gaussian splatting介绍整理
3D 高斯分布是用于实时辐射场渲染的 3D 高斯分布中描述的一种光栅化技术,它允许实时渲染从小图像样本中学习到的逼真场景。 paper github 本文翻译整理自: blog: Introduction to 3D Gaussian Splatting DDPMs - Part 2 给出一些2D图片,用…...

[C#]de4dot常用命令
命令:de4dot.exe "D:\xxx.exe" 解释:运行后文件在程序集的目录下生成一个带-cleaned的新程序集。 命令:de4dot.exe file1 -f "D:\xxx.exe" -o "D:\output\xxx_cleaned.exe" 解释:-f : 指定.NET 程序…...

林浩然的“生命体验”大冒险
林浩然的“生命体验”大冒险 Lin Haoran’s “Life Experience” Grand Adventure 在一个阳光明媚的日子,林浩然——我们这位幽默风趣、充满生活智慧的大男孩,正坐在自家后院的老槐树下,手捧一本哲学书,皱着眉头深思:“…...
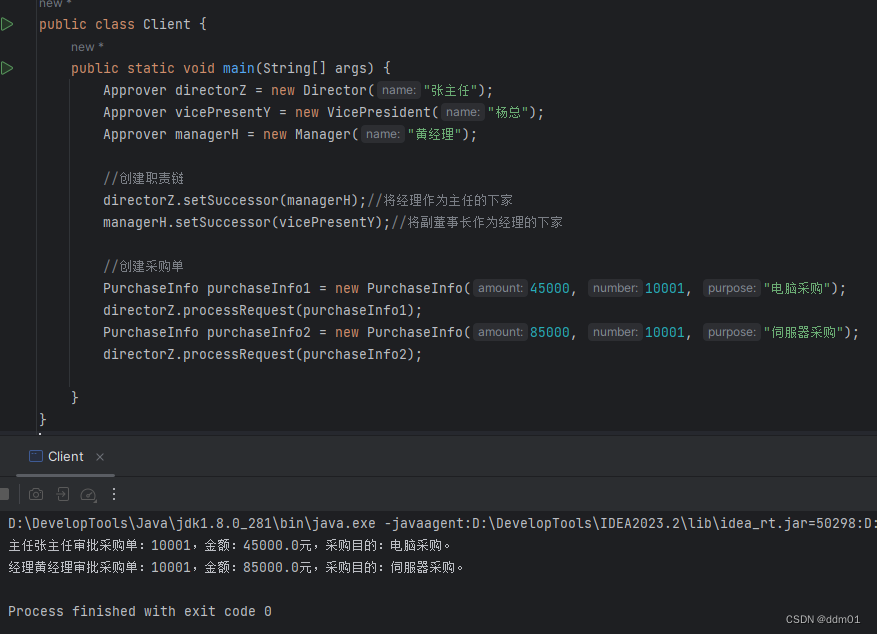
设计模式——职责链模式(Chain of Responsibility Pattern)
概述 职责链模式(Chain of Responsibility Pattern):避免请求发送者与接收者耦合在一起,让多个对象都有可能接收请求,将这些对象连接成一条链,并且沿着这条链传递请求,直到有对象处理它为止。职责链模式是一种对象行为…...

C++引用详解
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、引用的概念 引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内存空间…...

fMRI数据处理(随时更新)
要开始学习处理fMRI的数据了。 fMRI的数据一般有 dcm 格式和 nii 格式。 Nifti(Neuroimaging Informatics Technology Initiative,神经影像信息学技术倡议)文件格式,是目前各大神经影像分析工具普遍兼容的体素水平的数据格式&am…...

【Linux C | 网络编程】getsockname 和 getpeername函数详解及C语言例子
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...
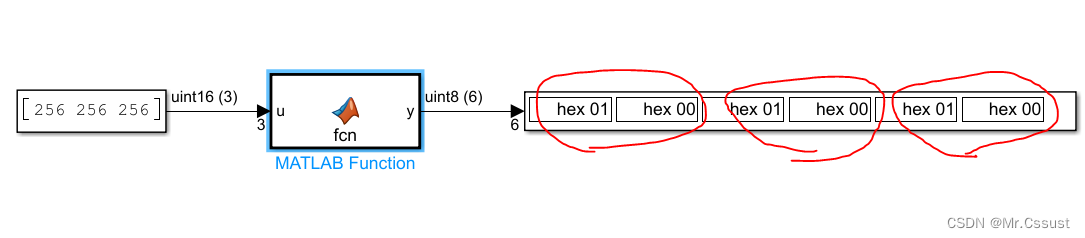
研发日记,Matlab/Simulink避坑指南(六)——字节分割Bug
文章目录 前言 背景介绍 问题描述 分析排查 解决方案 总结归纳 前言 见《研发日记,Matlab/Simulink避坑指南(一)——Data Store Memory模块执行时序Bug》 见《研发日记,Matlab/Simulink避坑指南(二)——非对称数据溢出Bug》…...
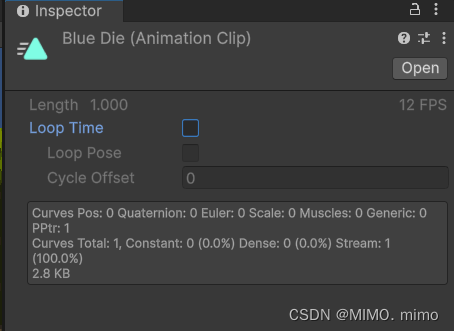
(M)unity受伤反弹以及死亡动画
受伤反弹 1.在人物控制脚本中添加受伤后速度将为0,并添加一个反弹的力 在刷新移动时,需要在没有受伤的状态 public bool isHurt; public float hurtForce; private void FixedUpdate() {if(!isHurt)Move(); }public void GetHurt(Transform attacker) …...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
