机器学习---无偏估计
1. 如何理解无偏估计
无偏估计:就是我认为所有样本出现的概率⼀样。 假如有N种样本我们认为所有样本出现概率都是
1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲 的平均值。数学期望本质就
是平均值。
2. 无偏估计为何叫做“无偏”?它要“估计”什么?
首先回答第⼀个问题:它要“估计”什么?
它要估计的是整体的数学期望(平均值)。
第⼆个问题:那为何叫做无偏?有偏是什么?
假设这个是⼀些样本的集合X = x1, x2, x3, ..., xn,我们根据样本估计整体的数学期望(平均值)。
因为正常求期望是加权和,什么叫加权和?![]() ,这个就叫加权和。
,这个就叫加权和。
每个样本出现概率不⼀样,概率大的乘起来就大,这个就产生偏重了(有偏估计)。
但是我们不知道某个样本出现的概率。比如你从别⼈口袋里面随机拿了3张钞票。两张是十块钱,
⼀张100 元,然后你想估计下他口袋里的剩下的钱平均下来每张多少钱(估计平均值)。
然后呢?无偏估计计算数学期望就是认为所有样本出现概率⼀样大,没有看不起哪个样本。
回到求钱的平均值的问题。无偏估计我们认为每张钞票出现概率都是1/2(因为只出现了10和100
这两种情况,所以是1/2。如果是出现1 10 100三种情况,每种情况概率则是1/3。
哪怕拿到了两张十块钱,我还是认为十块钱出现的概率和100元的概率⼀样。不偏心。
所以无偏估计,所估计的别⼈口袋每张钱的数学期望(平均值)= 10 ∗ 1/2 + 100 ∗ 1/2。
有偏估计那就是偏重那些出现次数多的样本。认为样本的概率是不⼀样的。 我出现了两次十块
钱,那么我认为十块钱的概率是2/3,100块钱概率只有1/3。
有偏所估计的别⼈口袋每张钱的数学期望(平均值)= 10 ∗ 2/3 + 100 ∗ 1/3。
3. 为何要用无偏估计?
因为现实生活中我不知道某个样本出现的概率,就像骰子,我不知道他是不是加过水银。 所以我
们暂时按照每种情况出现概率⼀样来算。
相关文章:
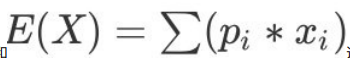
机器学习---无偏估计
1. 如何理解无偏估计 无偏估计:就是我认为所有样本出现的概率⼀样。 假如有N种样本我们认为所有样本出现概率都是 1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲 的平均值。数学期望本质就 是平均值。 2. 无偏估计为何叫做“无偏”࿱…...

C语言基础13
今天是学习嵌入式相关内容的第十四天,以下是今日所学内容 1.结构体: 1.结构体类型定义 2.结构体变量的定义 3.结构体元素的访问 4.结构体的存储 内存对齐 结构体整体的大小必须为最大基本类型长度的整数倍 5.结构体作为函数参数 值传递 练习:定…...

【Java】Maven配置加载到全局
Maven配置加载到全局 <build><plugins><plugin><artifactId>maven-resources-plugin</artifactId><configuration><encoding>utf-8</encoding><useDefaultDelimiters>true</useDefaultDelimiters></configura…...
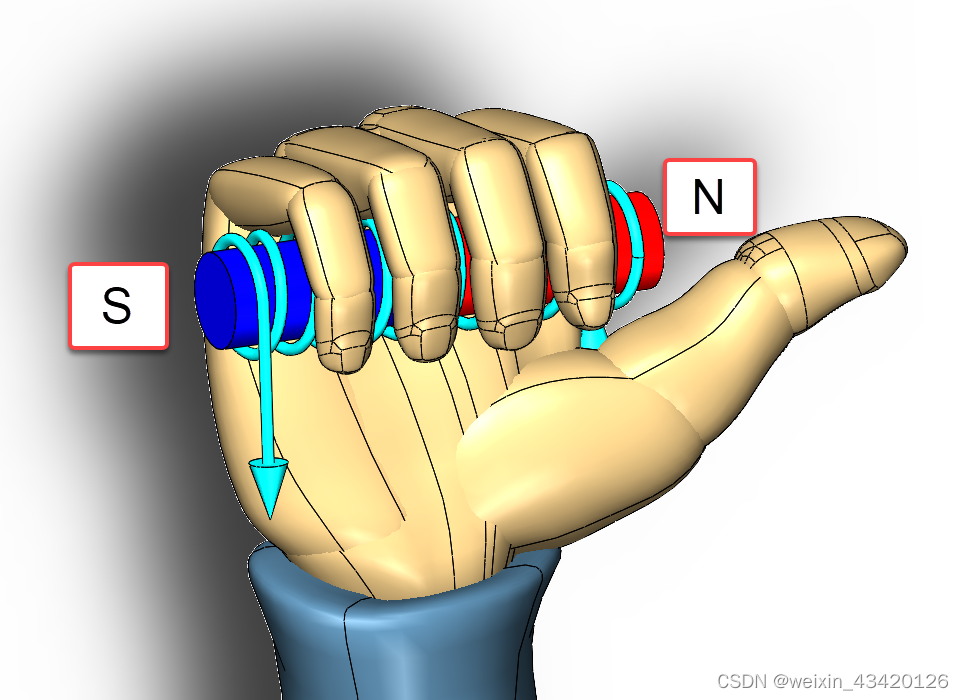
右手螺旋线定则
通电螺线管中的安培定则(安培定则二):用右手握住通电螺线管,让四指指向电流的方向,那么大拇指所指的那一端是通电螺线管的N极。...

2024 高级前端面试题之 React 「精选篇」
该内容主要整理关于 React 模块的相关面试题,其他内容面试题请移步至 「最新最全的前端面试题集锦」 查看。 React模块精选篇 1. 如何理解React State不可变性的原则2. JSX本质3. React合成事件机制4. setState和batchUpdate机制5. 组件渲染和更新过程6. Diff算法相…...
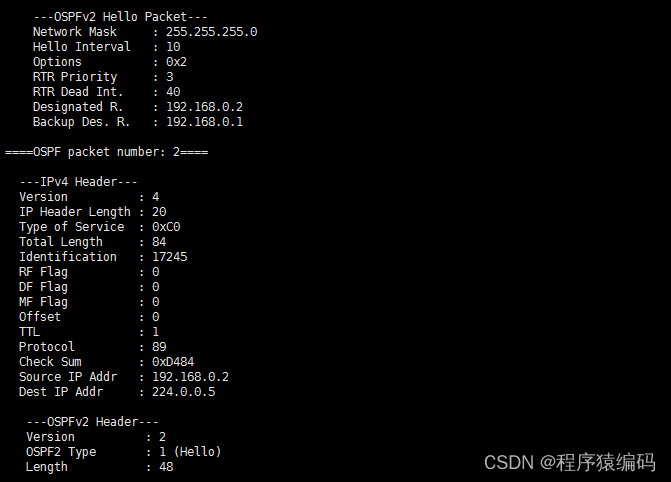
OSPF协议解析及相关技术探索(C/C++代码实现)
OSPF(开放最短路径优先)是一种用于自治系统(AS)内部的路由协议,它是基于链路状态算法的。OSPF的设计目的是为了提供一种可扩展、快速收敛和高效的路由解决方案。 OSPF概念和特点 概念 自治系统(AS&#…...
如何恢复已删除的照片?
在这篇综合文章中发现恢复丢失照片的有效且免费的方法。无论您使用的是智能手机、iPhone、Windows 计算机、Mac、SD 卡还是数码相机,我们都提供有关如何恢复已删除照片的分步说明。此外,学习一些有价值的技巧,以防止将来意外删除照片。 意外…...
VMware虚拟机安装macOS
VMware虚拟机安装macOS 文章目录 VMware虚拟机安装macOS先看效果一、准备工作①:镜像资源下载②:虚拟机③:安装macOS所必要的插件 二、开始安装①:创建新的虚拟机②:自定义硬件③:开启虚拟机 先看效果 一、…...
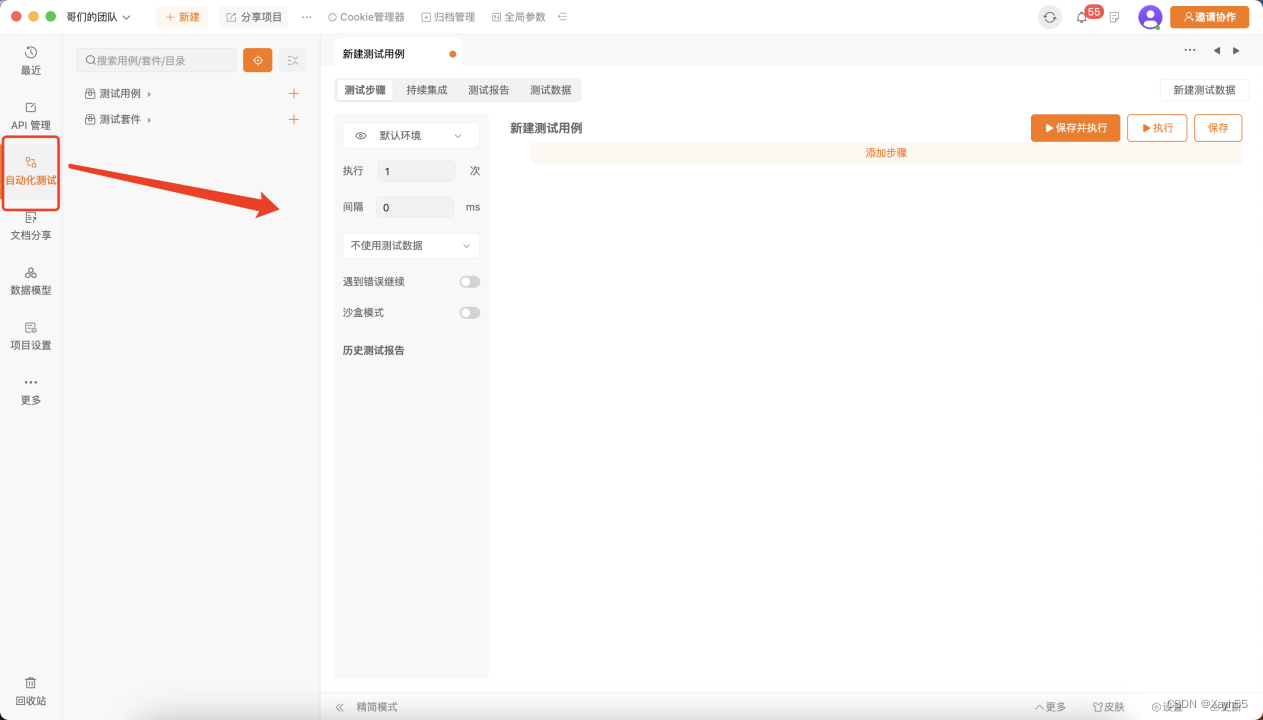
API管理协作工具:Apipost
相信无论是前端,还是后端的测试和开发人员,都遇到过这样的困难。不同工具之间数据一致性非常困难、低效。多个系统之间数据不一致,导致协作低效、频繁出问题,开发测试人员痛苦不堪。 API管理的难点在哪? 开发人员在 …...
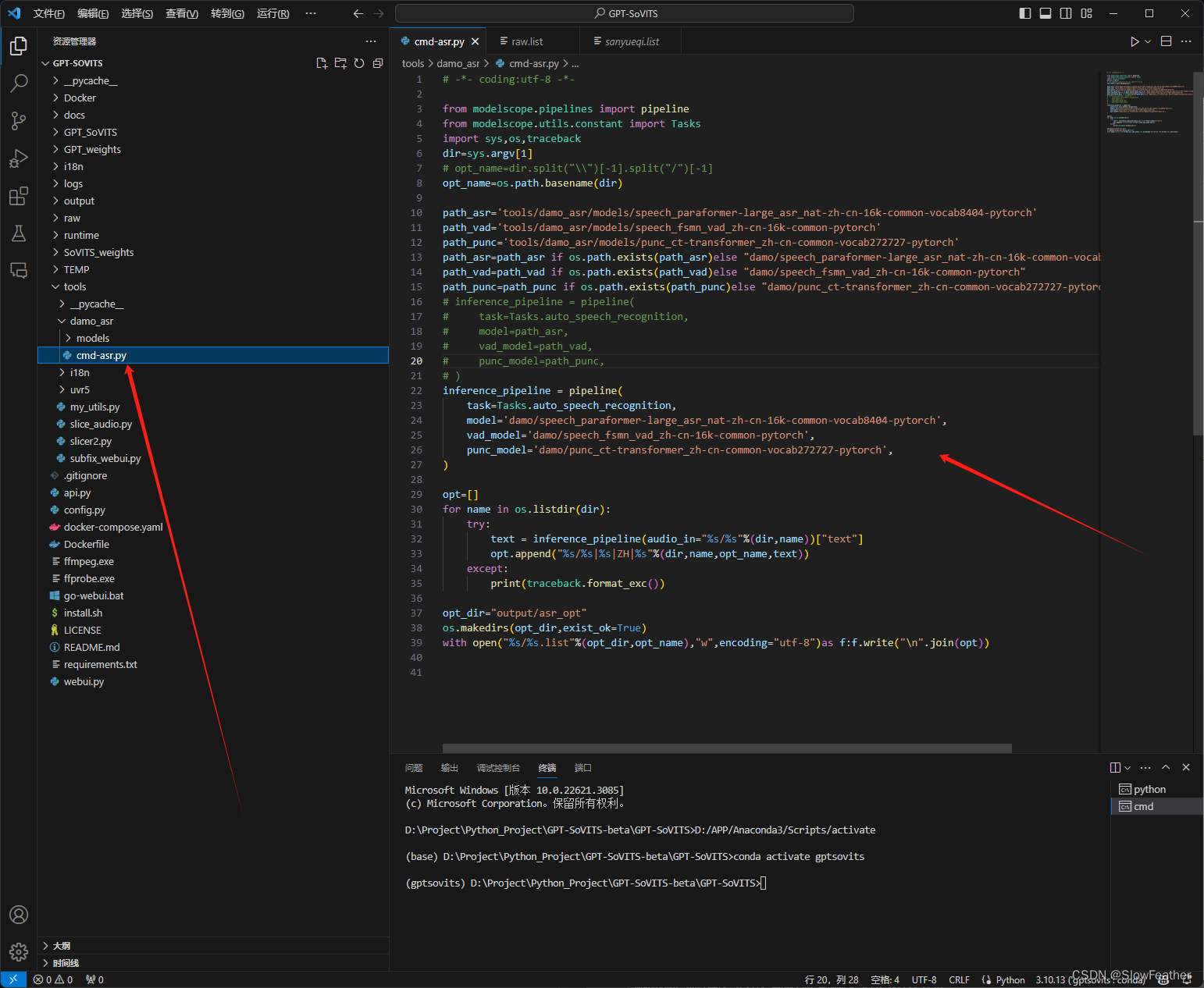
GPT-SoVITS 本地搭建踩坑
GPT-SoVITS 本地搭建踩坑 前言搭建下载解压VSCode打开安装依赖包修改内容1.重新安装版本2.修改文件内容 运行总结 前言 传言GPT-SoVITS作为当前与BertVits2.3并列的TTS大模型,于是本地搭了一个,简单说一下坑。 搭建 下载 到GitHub点击此处下载 http…...
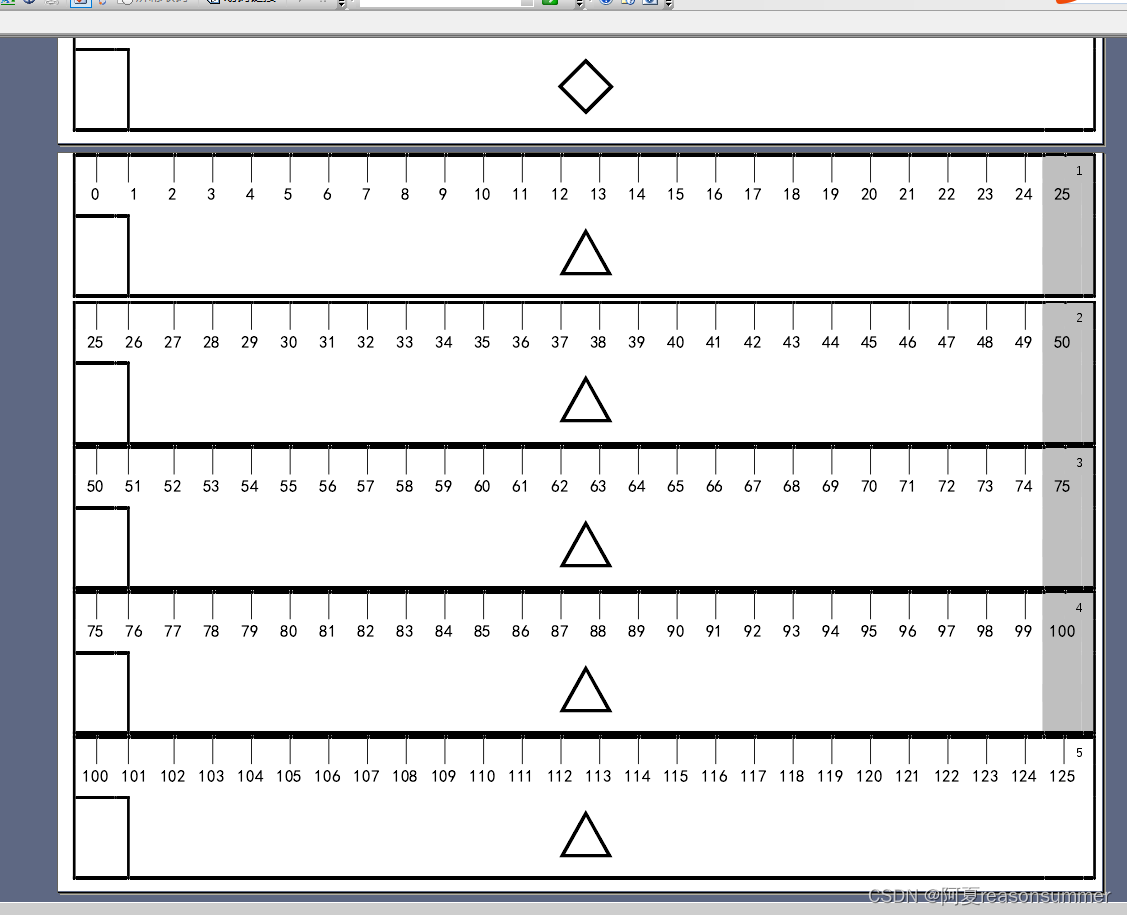
【教学类-34-02】20240130纸尺2.0 (A4横版5条,刻度25*5=125CM,有图案)
作品展示: 背景需求: 设计了纸尺的基本模板 【教学类-34-01】20240130纸尺1.0 (A4横版5条,刻度25*5125CM)-CSDN博客文章浏览阅读194次,点赞5次,收藏5次。【教学类-34-01】20240130纸尺1.0 &am…...
iText操作pdf
最近有个任务是动态的创建pdf根据获取到的内容,百度到的知识点都比较零散,官方文档想必大家也不容易看懂。下文是我做出的汇总 public class CreatePdfUtils {public static void create(){//准备File file new File("C:\\code\\base-project-back…...

关于SQLite 的下载与使用。配合python
win系统下: SQLite Download Page Precompiled Binaries for Windows sqlite-tools-win-x64-3450000.zip (4.77 MiB) 解压后,找个位置。然后设置环境变量指定位置。 可以手动建立.db文件。 也可以通过代码建立: 如下代码就是建立一个db文件。…...

java面向对象基础(面试)
一、面向对象基础 1. 面向对象和面向过程的区别 面向过程把解决问题的过程拆成一个个方法,通过一个个方法的执行解决问题。面向对象会先抽象出对象,然后用对象执行方法的方式解决问题。 2.创建一个对象用什么运算符?对象实体与对象引用有何不同? n…...

【C++修行之道】STL(初识list、stack)
目录 一、list 1.1list的定义和结构 以下是一个示例,展示如何使用list容器: 1.2list的常用函数 1.3list代码示例 二、stack 2.1stack的定义和结构 stack的常用定义 2.2常用函数 2.3stack代码示例 一、list 1.1list的定义和结构 list的使用频率不高&#…...
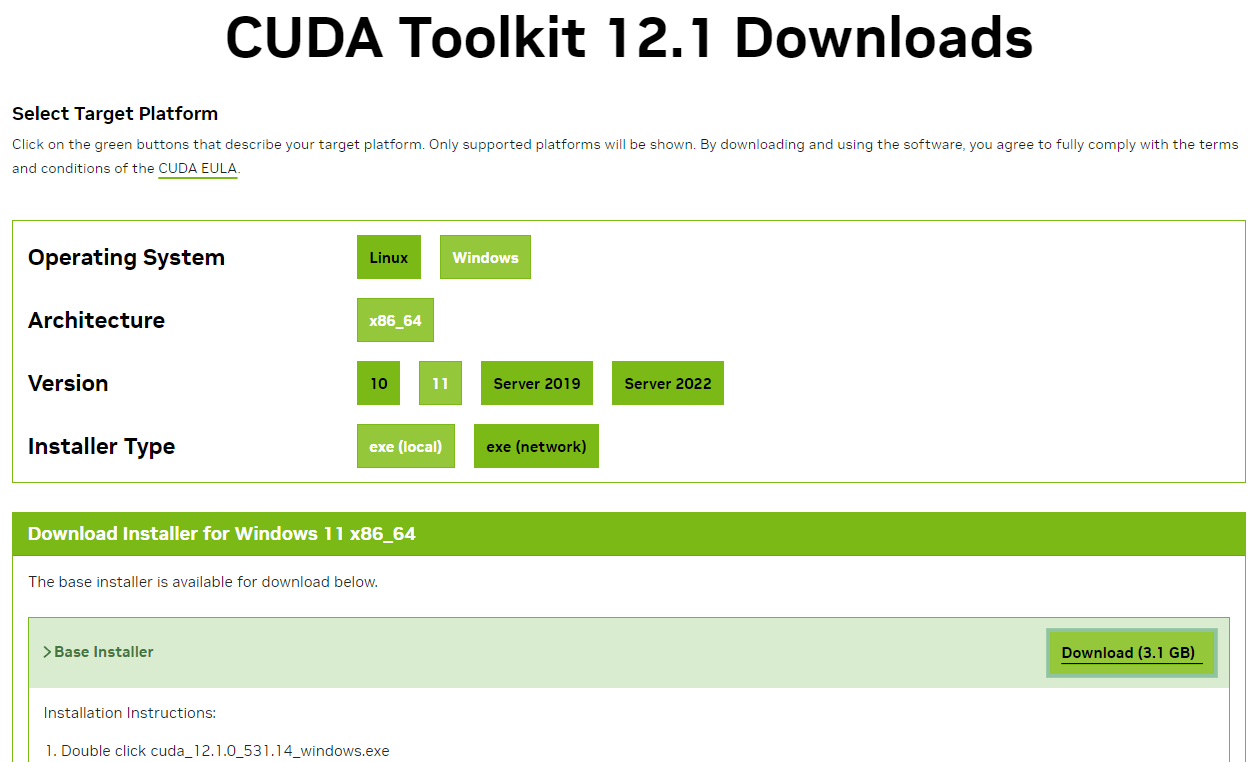
【环境配置】安装了pytorch但是报错torch.cuda.is_availabel()=Flase
解决思路:import torch正常,说明torch包安装正常,但是不能和gpu正常互动,猜测还是pytroch和cuda的配合问题 1.查看torch包所需的cuda版本 我的torch是2.0.1,在现在是比较新的包,需要12以上的cuda支持&…...

什么是模板方法模式?它的实现方式有哪些?
什么是模板方法模式?它的实现方式有哪些? 模板方法模式是一种行为型模式,它定义了一个操作中的算法骨架,而将算法的一些步骤延迟到子类中实现,使得子类可以不改变该算法结构的情况下重定义该算法的某些特定步骤。 模…...
)
java:实现查询MySQL数据库中的数据,并导出excel、pdf类型文档(超详细)
查询MySQL数据库中数据,导出excel、pdf类型文档 1.数据库表格 CREATE TABLE user (id int NOT NULL AUTO_INCREMENT COMMENT 编号,name varchar(255) DEFAULT NULL COMMENT 姓名,age int DEFAULT NULL COMMENT 年龄,addr varchar(255) DEFAULT NULL COMMENT 住址1…...
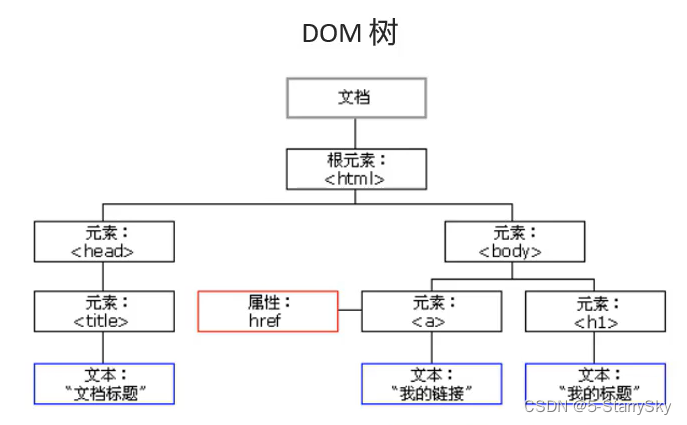
Java后端须知的前端知识
Java后端须知的前端知识 HTML (超文本标记语言) W3C标准 结构:HTML表现:CSS行为:JavaScript 快速入门 <html><head><title></title></head><body><font color"red&q…...

Servlet基础之URL匹配规则
文章目录 URL 匹配规则几个容易混淆的规则精确匹配路径匹配扩展名匹配缺省匹配注意事项 1:匹配规则不能混用注意事项 2:"\/\*" 和 "/" 含义并不相同 URL 匹配规则 几个容易混淆的规则 servlet 容器中的匹配规则既不是简单的通配&am…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
