C语言第十四弹---函数递归

✨个人主页: 熬夜学编程的小林
💗系列专栏: 【C语言详解】 【数据结构详解】
函数递归
1、递归是什么?
1.1、递归的思想
1.2、递归的限制条件
2、递归举例
2.1、举例1:求n的阶乘
2.1.1、分析和代码实现
2.1.2、画图推演
2.2、举例2:顺序打印⼀个整数的每⼀位
2.2.1、分析和代码实现
2.2.2、画图推演
3、递归与迭代
3.1、举例3:求第n个斐波那契数
总结
1、递归是什么?
#include <stdio.h>
int main()
{printf("hehe\n");main();//main函数中又调用了main函数return 0;
}
1.1、递归的思想
把⼀个大型复杂问题层层转化为⼀个与原问题相似,但规模较小的子问题来求解;直到子问题不能再被拆分,递归就结束了。所以递归的思考方式就是把 大事化小的过程。
1.2、递归的限制条件
• 递归存在限制条件,当满足这个限制条件的时候,递归便不再继续。• 每次递归调用之后越来越接近这个限制条件。
2、递归举例
2.1、举例1:求n的阶乘
2.1.1、分析和代码实现
举例:5! = 5*4*3*2*14! = 4*3*2*1所以:5! = 5*4!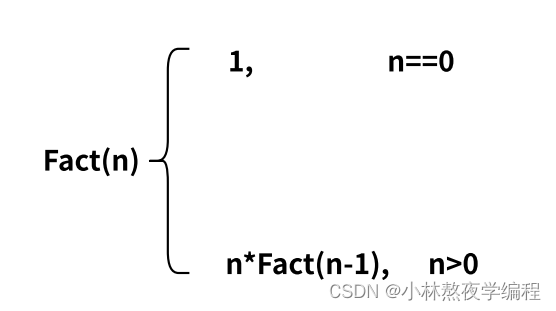
int Fact(int n)
{if(n==0)return 1;elsereturn n*Fact(n-1);
}#include <stdio.h>
int Fact(int n)
{if(n==0)return 1;elsereturn n*Fact(n-1);
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fact(n);printf("%d\n", ret);return 0;
}
2.1.2、画图推演
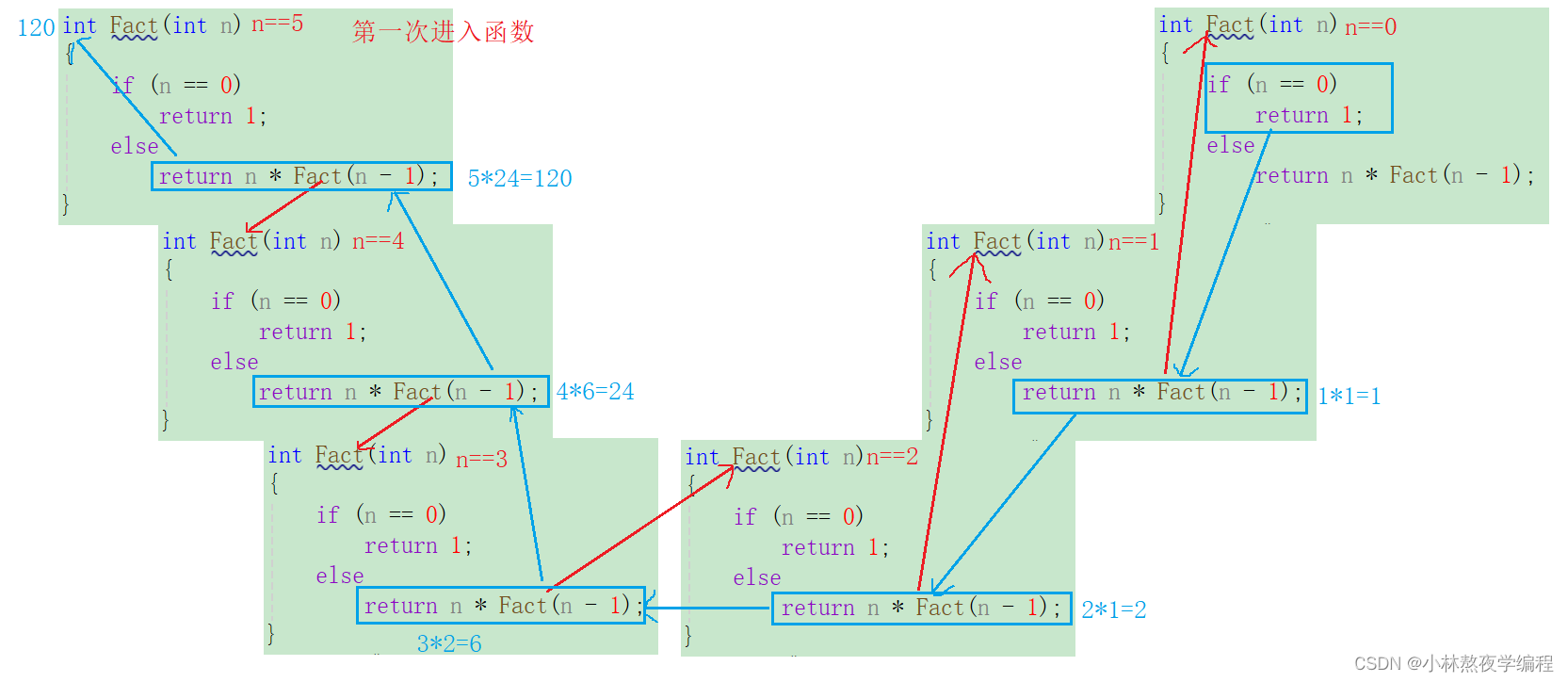
2.2、举例2:顺序打印⼀个整数的每⼀位
2.2.1、分析和代码实现
如果n是⼀位数,n的每⼀位就是n自己;n是超过1位数的话,就得拆分每⼀位。
Print(n)
如果n是1234,那表示为
Print(1234) //打印1234的每⼀位
其中1234中的4可以通过%10得到,那么
Print(1234)就可以拆分为两步:
1. Print(1234/10) //打印123的每⼀位
2. printf(1234%10) //打印4完成上述2步,那就完成了1234每⼀位的打印
那么Print(123)⼜可以拆分为Print(123/10) + printf(123%10)Print(1234)
==>Print(123) + printf(4)
==>Print(12) + printf(3)
==>Print(1) + printf(2)
==>printf(1)那么代码完成也就比较清楚:
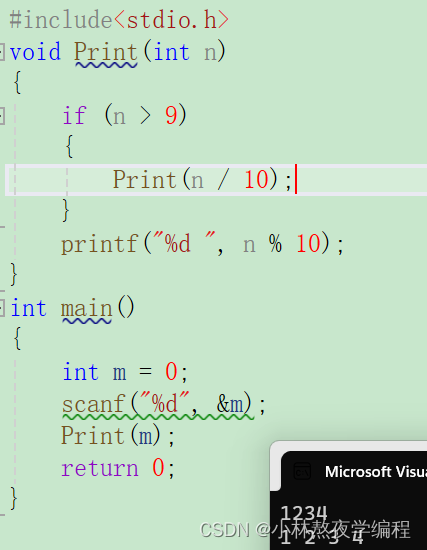
void Print(int n)
{
if(n>9)
{
Print(n/10);
}
printf("%d ", n%10);
}
int main()
{
int m = 0;
scanf("%d", &m);
Print(m);
return 0;
}
2.2.2、画图推演
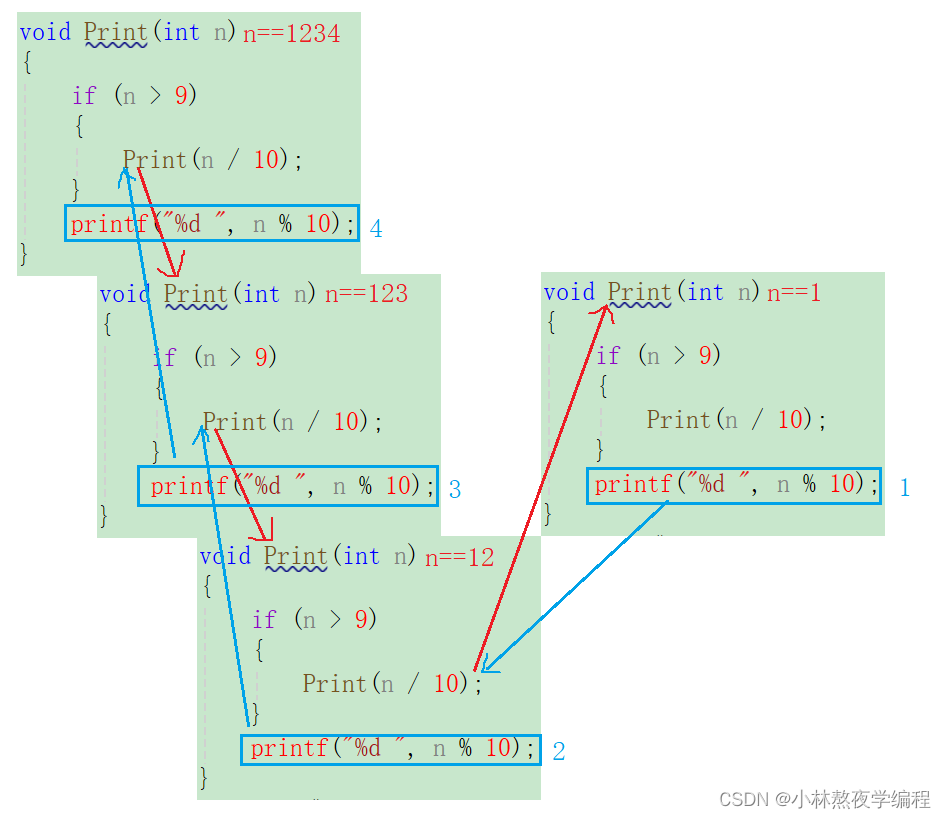
3、递归与迭代
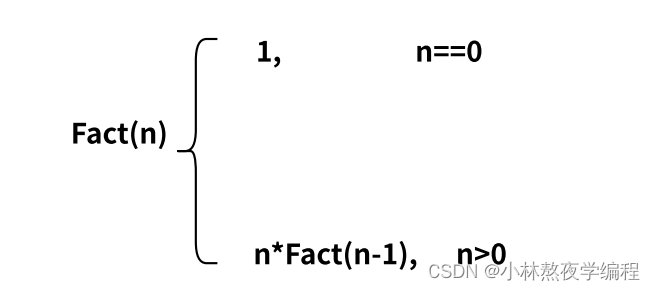
int Fact(int n)
{if(n==0)return 1;elsereturn n*Fact(n-1);
}int Fact(int n)
{int i = 0;int ret = 1;for(i=1; i<=n; i++){ret *= i;}return ret;
}3.1、举例3:求第n个斐波那契数
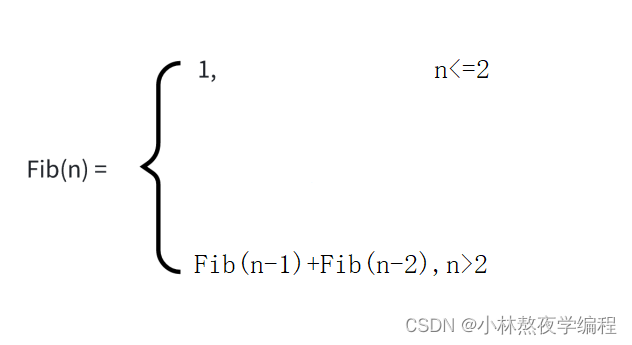
int Fib(int n)
{if(n<=2)return 1;elsereturn Fib(n-1)+Fib(n-2);
}#include <stdio.h>
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret); return 0;
}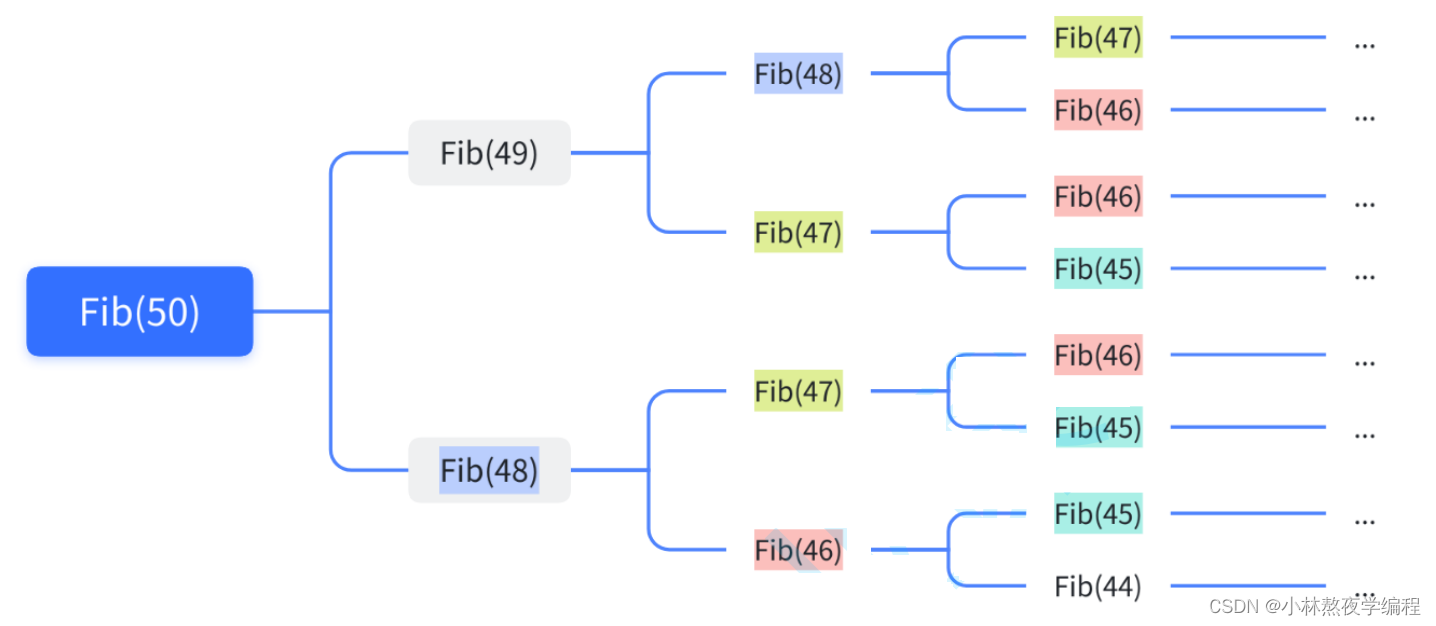
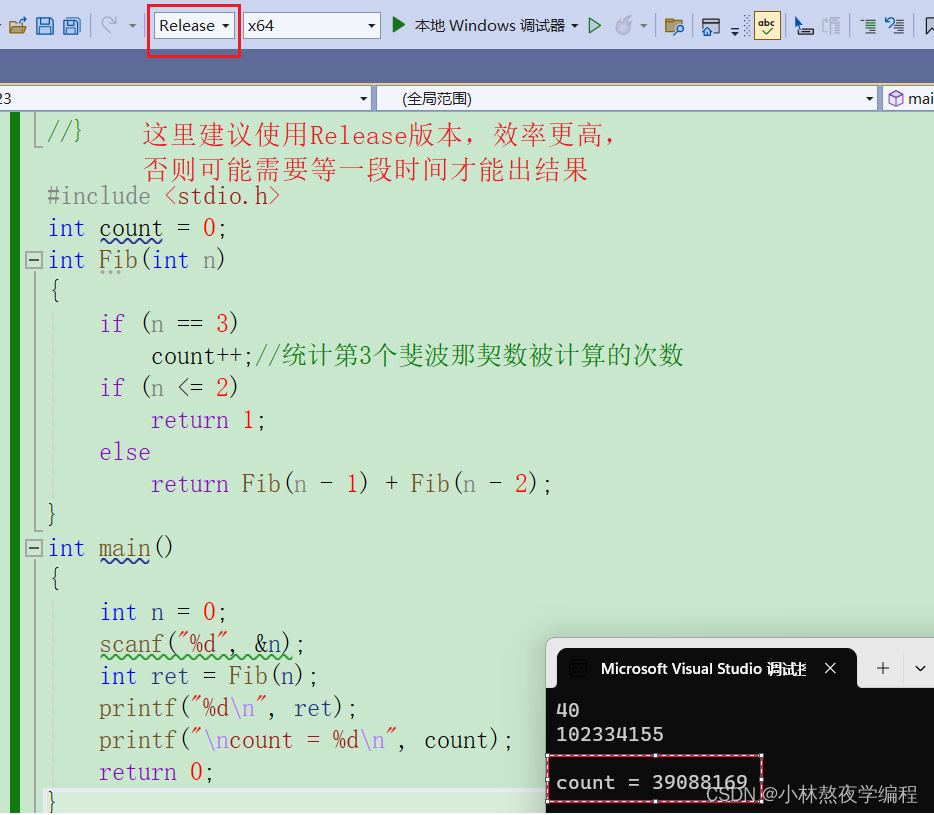
#include <stdio.h>
int count = 0;
int Fib(int n)
{if(n == 3)count++;//统计第3个斐波那契数被计算的次数if(n<=2)return 1;elsereturn Fib(n-1)+Fib(n-2);
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret); printf("\ncount = %d\n", count);return 0;
}
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while(n>2){c = a+b;a = b;b = c;n--;}return c;
}总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!
相关文章:

C语言第十四弹---函数递归
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 函数递归 1、递归是什么? 1.1、递归的思想 1.2、递归的限制条件 2、递归举例 2.1、举例1:求n的阶乘 2.1.1、分析和代码实现 2.1.2、…...
etcd自动化安装配置教程
文章目录 前言一、简介1. 简介2. 特点3. 端口介绍 二、etcd安装教程(单机版)1. 复制脚本2. 增加执行权限3. 执行脚本4. 查看启动状态5. 卸载etcd 三、etcd安装教程(集群版)1. 复制脚本2. 增加执行权限3. 分发脚本4. 执行脚本5. 启…...
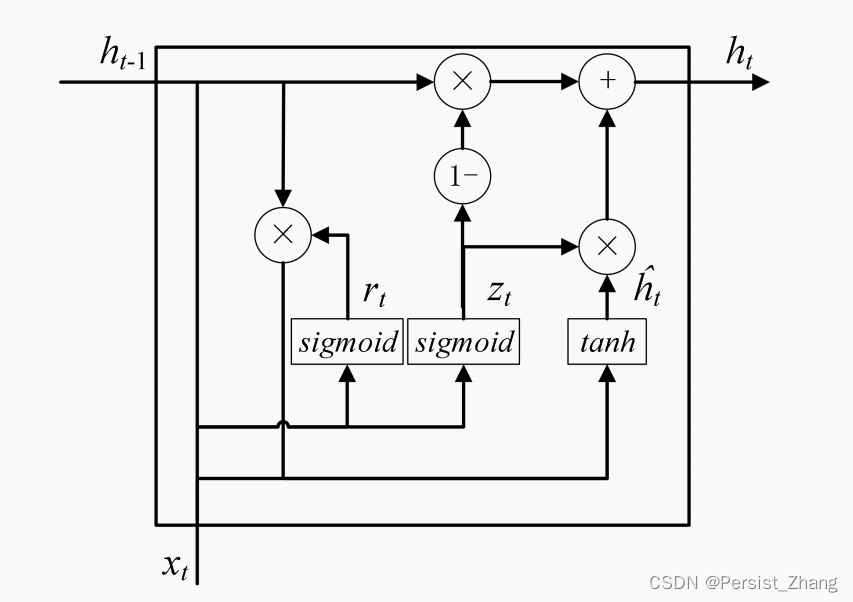
时间序列预测——GRU模型
时间序列预测——GRU模型 在深度学习领域,循环神经网络(RNN)是处理时间序列数据的一种常见选择。上期已介绍了LSTM的单步和多步预测。本文将深入介绍一种LSTM变体——门控循环单元(GRU)模型,包括其理论基础…...
通用CI/CD软件平台TeamCity全新发布v2023.11——增强Git托管平台的集成
TeamCity是一个通用的 CI/CD 软件平台,可以实现灵活的工作流、协作和开发做法。我们的解决方案将帮助在您的 DevOps 流程中成功实现持续集成、持续交付和持续部署。 TeamCity 2023.11正式版下载 TeamCity 2023.11 带来了矩阵构建和构建缓存等多项备受期待的功能&a…...

C语言:register类型变量
register—— 寄存器存储 register 是 C 语言中的一种存储类别(Storage Class),它用于告诉编译器将变量存储在寄存器中。在 C 语言中,变量的存储位置可以是寄存器、堆栈或静态存储区,使用 register 存储类别可以帮助我…...
android 自定义下拉框
一、 简介: 原生Android 提供的spinner下拉框不怎么方便,样式有点丑。修改起来麻烦,于是就自己动手写了一下拉列表。 实现原理使用的是,popwindow弹框,可实现宽高自定义,下拉列表使用listview. 二、pop弹框…...
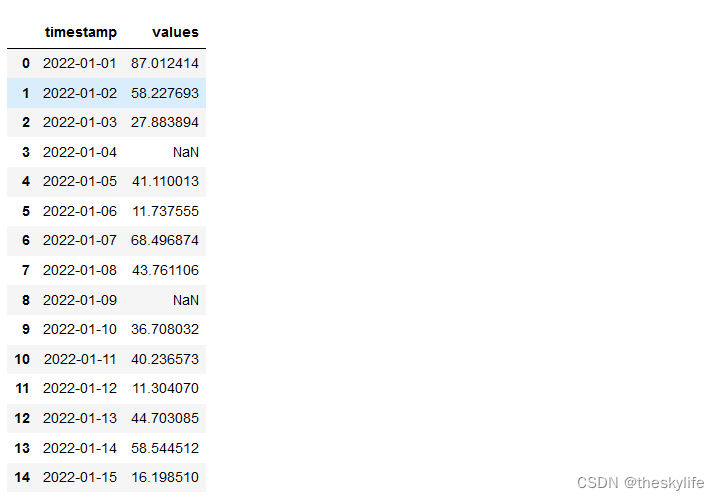
揭开时间序列的神秘面纱:特征工程的力量
目录 写在开头1. 什么是特征工程?1.1 特征工程的定义和基本概念1.2 特征工程在传统机器学习中的应用1.3 时间序列领域中特征工程的独特挑战和需求3. 时间序列数据的特征工程技术2.1 数据清洗和预处理2.1.1 缺失值处理2.1.2 异常值检测与处理2.2 时间特征的提取2.2.1 时间戳解析…...

vue3 源码解析(5)— patch 函数源码的实现
什么是 patch 在 vue 中 patch 函数的作用是在渲染的过程中,比较新旧节点的变化,通过打补丁的形式,进行新增、删除、移动或替换操作,此过程避免了大量的 dom 操作,提升了运行的性能。 patch 执行流程 patch 函数整体…...
蓝桥杯2024/1/28----十二届省赛题笔记
题目要求: 2、 竞赛板配置要求 2.1将 IAP15F2K61S2 单片机内部振荡器频率设定为 12MHz。 2.2键盘工作模式跳线 J5 配置为 KBD 键盘模式。 2.3扩展方式跳线 J13 配置为 IO 模式。 2.4 请注意 : 选手需严格按照以上要求配置竞赛板,编写和调…...
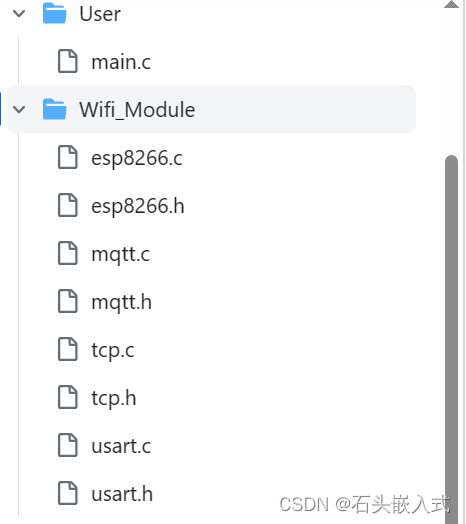
STM32+ESP8266 实现物联网设备节点
目录 一、硬件准备 二、编译环境 三、源代码地址 四、说明 五、测试方法 六、所有测试工具和文档 本项目使用stm32F103ZEesp8266实现一个物联网的通信节点,目前支持的协议有mqtt,tcp。后续会持续更新,增加JSON,传感器&#…...

免费的ChatGPT网站(7个)
还在为找免费的chatGPT网站或者应用而烦恼吗?博主归纳总结了7个国内非常好用,而且免费的chatGPT网站,AI语言大模型,我们都来接触一下吧。 免费!免费!免费!...,建议收藏保存。 1&…...
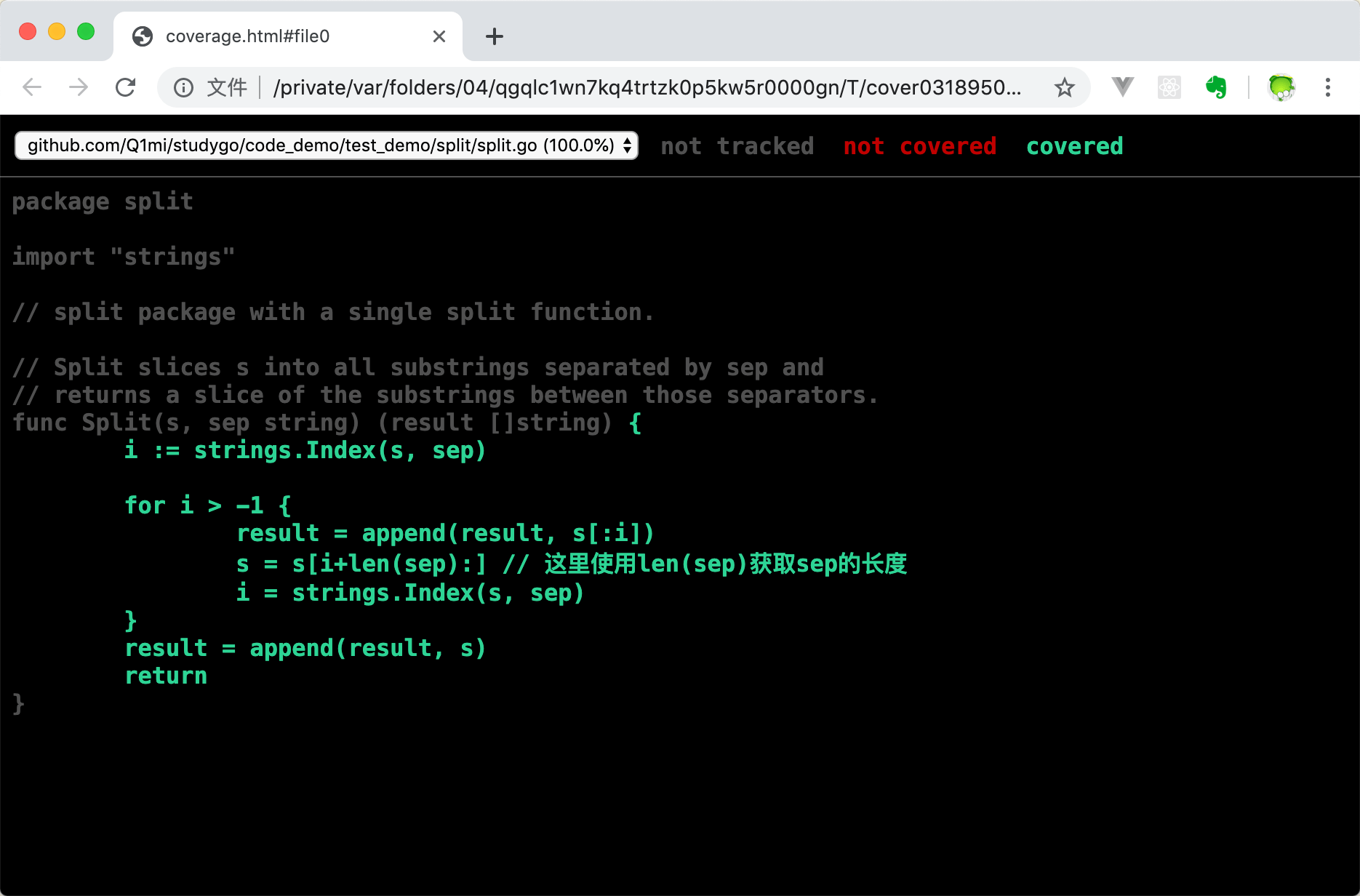
Go语言基础之单元测试
1.go test工具 Go语言中的测试依赖go test命令。编写测试代码和编写普通的Go代码过程是类似的,并不需要学习新的语法、规则或工具。 go test命令是一个按照一定约定和组织的测试代码的驱动程序。在包目录内,所有以_test.go为后缀名的源代码文件都是go …...
)
C++ easyX小程序(介绍几个函数的使用)
本小程序通过代码和注释,介绍了easyX窗口及控制台窗口的设置方法;还介绍了easyX中关于颜色、线型、画圆、画方、显示文字以及鼠标消息处理等函数的使用方法。为便于理解,本程序同时使用控制台和easyX窗口,由控制台控制程序运行、由…...

配置nginx以成功代理websocket
配置nginx以成功代理websocket 在使用socket.io的时候遇到这样一个问题:websocket接收的消息的顺序错位了,然后看了一下浏览器的console的报错,提示连接到ws失败,然后在浏览器的开发者工具的网络中看了一下ws对应的消息里面报错&…...

代码随想录算法训练营第二十二天|235.二叉搜索树的最近公共祖先、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点
文档讲解: BST,各种插入删除操作 235.二叉搜索树的最近公共祖先 思路:昨天练习了二叉树的搜索,今天这道题是二叉搜索树的搜索,其具有有序这个特点,其能决定我们每次搜索是进入该节点的左子树还是右子树&…...
)
collection、ofType、select的联合用法(Mybatis实现树状结构查询)
需求 得到树结构数据也可以用lambda表达式也行,也可以直接循环递归也行,本文采用的是直接在Mybatis层得到结果,各有各的优势。 代码 1、实体类 Data public class CourseChapterVO implements Serializable {private static final long s…...

FLUENT Meshing Watertight Geometry工作流入门 - 4 局部加密区域
本视频中学到的内容: 使用Watertight Geometry Workflow 的 Create Local Refinement Regions 任务来创建细化的网格区域 视频链接: FLUENT Meshing入门教程-4创建局部加密区域_哔哩哔哩_bilibili 可以通过使用 Watertight Geometry Workflow 的 Create…...
前端添加富文本/Web 富文本编辑器wangeditor
官网wangEditor 需要引入两个文件 <link href"https://unpkg.com/wangeditor/editorlatest/dist/css/style.css" rel"stylesheet"> <script src"https://unpkg.com/wangeditor/editorlatest/dist/index.js"></script> 前端…...

软件价值2-贪吃蛇游戏
贪吃蛇游戏虽然很多,不过它可以作为软件创作的开端,用python来实现,然后dist成windows系统可执行文件。 import pygame import sys import random# 初始化 pygame.init()# 游戏设置 width, height 640, 480 cell_size 20 snake_speed 15# …...

应用案例 | 基于三维机器视觉的汽车副车架在线测量解决方案
在汽车制造领域中,精确的测量是确保产品质量和生产效率的关键。随着科技的不断进步,测量技术也在不断精进。 副车架是汽车底盘的重要组成部分,负责支撑引擎,是车辆结构中至关重要的组成部分之一,其制造质量直接关系到汽…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
