C语言第十五弹---操作符(上)

✨个人主页: 熬夜学编程的小林
💗系列专栏: 【C语言详解】 【数据结构详解】
操作符
1、操作符的分类
2、二进制和进制转换
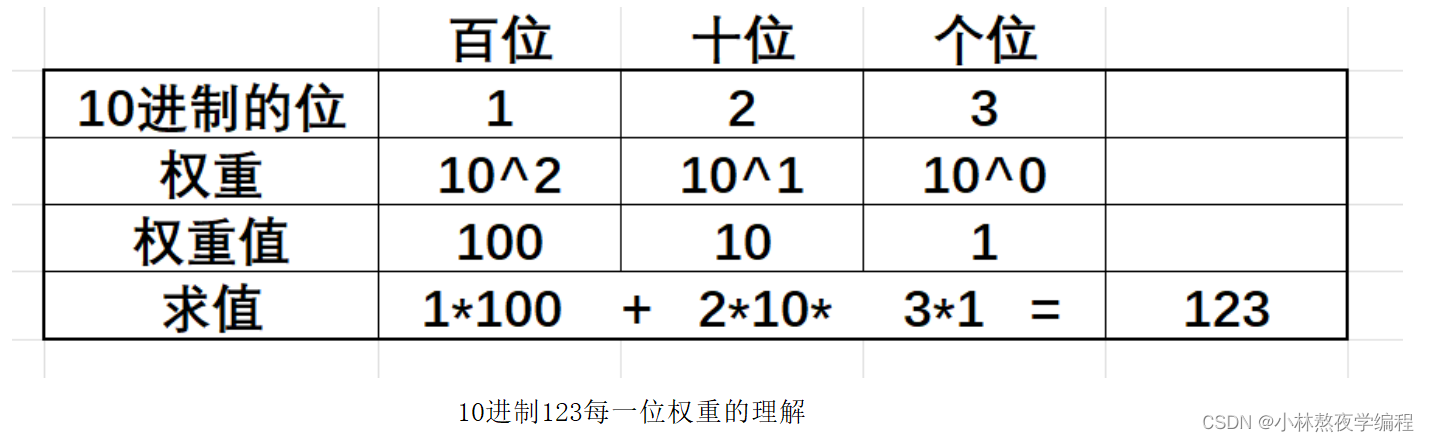
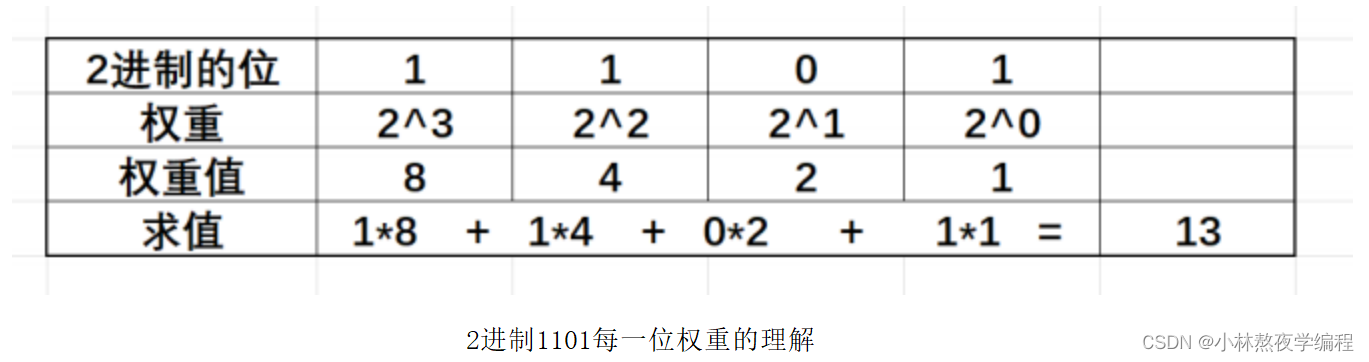
2.1、2进制转10进制
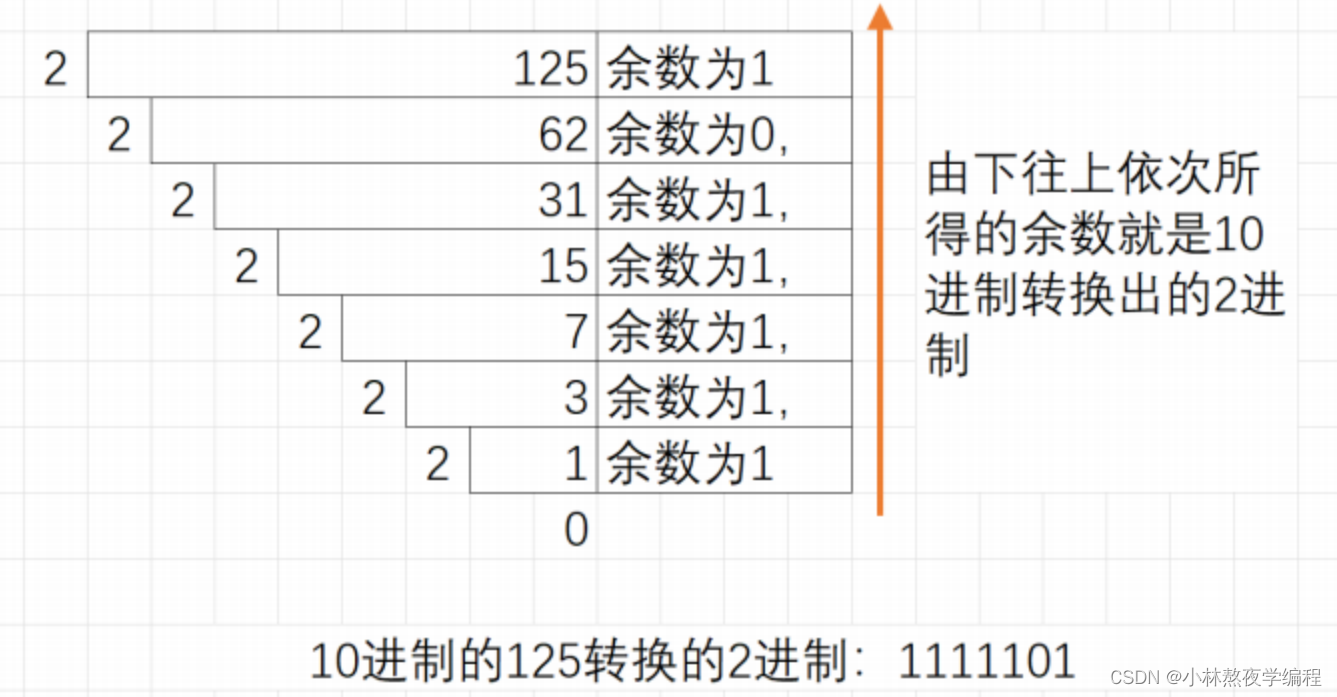
2.1.1、10进制转2进制数字
2.2、2进制转8进制和16进制
2.2.2、2进制转16进制
3. 原码、反码、补码
4. 移位操作符
4.1 左移操作符
4.2 右移操作符
5. 位操作符:&、|、^、~
6. 单目操作符
7. 逗号表达式
总结
1、操作符的分类
• 算术操作符: + 、 - 、 * 、 / 、 %• 移位操作符: << >>• 位操作符: & | ^ ~• 赋值操作符: = 、 += 、 -= 、 *= 、 /= 、 %= 、 <<= 、 >>= 、 &= 、 |= 、 ^=• 单目操作符: !、 ++ 、 -- 、 & 、 * 、 + 、 - 、 ~ 、 sizeof 、 ( 类型 )• 关系操作符: > 、 >= 、 < 、 <= 、 == 、 !=• 逻辑操作符: && 、 ||• 条件操作符: ? :• 逗号表达式: ,• 下标引用: []• 函数调用: ()• 结构成员访问: . 、 ->
2、二进制和进制转换
15的2进制:1111
15的8进制:17
15的10进制:15
15的16进制:F2.1、2进制转10进制
2.1.1、10进制转2进制数字
2.2、2进制转8进制和16进制

2.2.2、2进制转16进制

3. 原码、反码、补码
原码:直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。补码:反码+1就得到补码。
在计算机系统中,数值⼀律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统⼀处理;同时,加法和减法也可以统⼀处理(CPU只有加法器),此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
4. 移位操作符
4.1 左移操作符
#include <stdio.h>
int main()
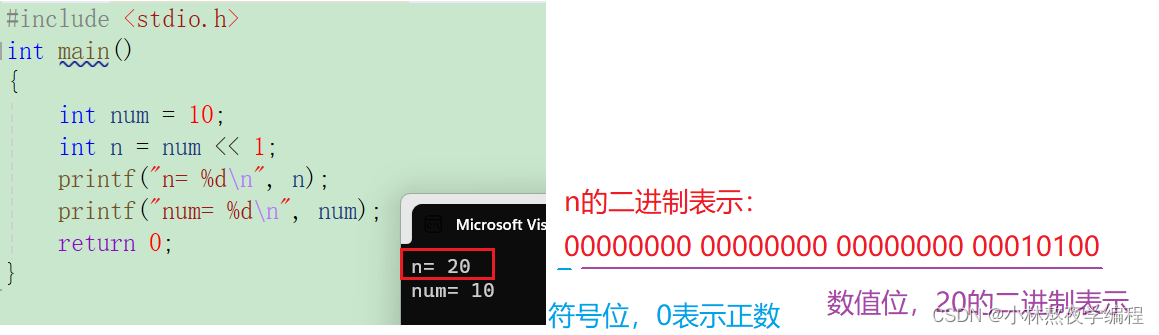
{int num = 10;int n = num<<1;printf("n= %d\n", n);printf("num= %d\n", num);return 0;
}

4.2 右移操作符
#include <stdio.h>
int main()
{int num = -10;int n = num>>1;printf("n= %d\n", n);printf("num= %d\n", num);return 0;
}
此处暂时记住结论,VS右移时遵守算术右移。后序会详细讲解。
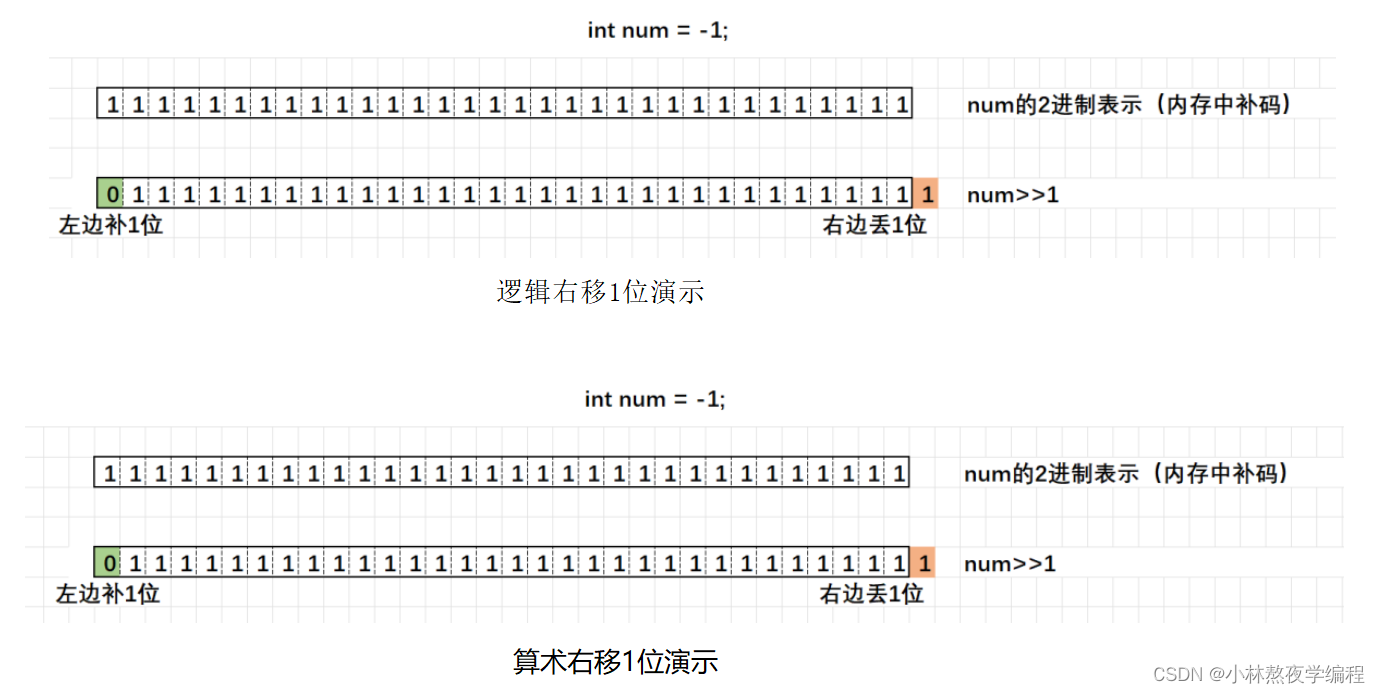
int num = 10;
num>>-1;//error5. 位操作符:&、|、^、~
& //按位与 1&1=1 1&0=0 0&0=0 同时为真才为真
| //按位或 1|0=1 1|1=1 0|0=0 一个为真则为真
^ //按位异或 相同为0 相异为1
~ //按位取反 ~0为1 ~1为0#include <stdio.h>
int main()
{int num1 = 3;int num2 = 5;printf("%d\n", num1 & num2);printf("%d\n", num1 | num2);printf("%d\n", num1 ^ num2);printf("%d\n", ~0);return 0;
}
#include <stdio.h>
int main()
{int a = 10;int b = 20;a = a^b;b = a^b;a = a^b;printf("a = %d b = %d\n", a, b);return 0;
}
参考代码:
//方法1
#include <stdio.h>
int main()
{int num = 10;int count= 0;//计数while(num){if(num%2 == 1)count++;num = num/2;}printf("二进制中1的个数 = %d\n", count);return 0;
}
//思考这样的实现⽅式有没有问题?
如上图所示,如果为-10,次代码就有问题,因为负数原反补码不相同。
//方法2:
#include <stdio.h>
int main()
{int num = -1;int i = 0;int count = 0;//计数for(i=0; i<32; i++){if( num & (1 << i) )count++; }printf("⼆进制中1的个数 = %d\n",count);return 0;
}
//思考还能不能更加优化,这⾥必须循环32次的。//⽅法3:
#include <stdio.h>
int main()
{int num = -1;int i = 0;int count = 0;//计数while(num){count++;num = num&(num-1);}printf("⼆进制中1的个数 = %d\n",count);return 0;
}
//这种⽅式是不是很好?达到了优化的效果,但是难以想到。13的2进制序列: 00000000000000000000000000001101
将第5位置为1后:00000000000000000000000000011101
将第5位再置为0:00000000000000000000000000001101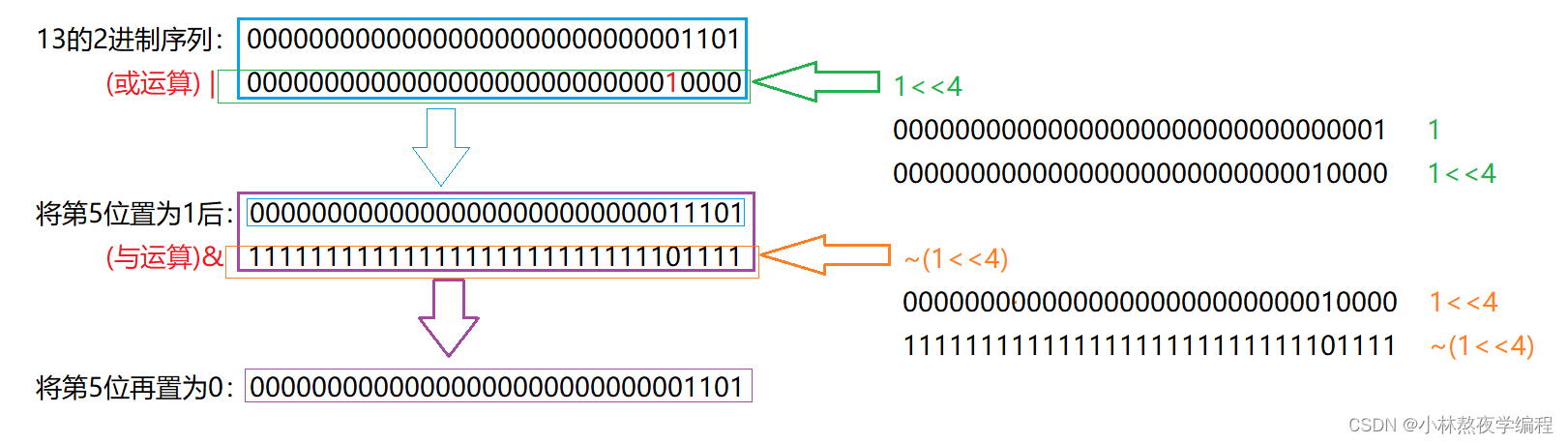
#include <stdio.h>
int main()
{int a = 13;a = a | (1<<4);printf("a = %d\n", a);a = a & ~(1<<4);printf("a = %d\n", a);return 0;
}6. 单目操作符
!、 ++ 、 -- 、 & 、 * 、 + 、 - 、 ~ 、 sizeof 、 ( 类型 )
7. 逗号表达式
exp1, exp2, exp3, …expN逗号表达式,就是用逗号隔开的多个表达式。逗号表达式,从左向右依次执行。整个表达式的结果是最后⼀个表达式的结果。
//代码1
#include<stdio.h>
int main()
{int a = 1;int b = 2;int c = (a > b, a = b + 10, a, b = a + 1);//逗号表达式//c是多少?printf("c = %d\n", c);return 0;
}
int a = 1;
int b = 2;
int c = (a > b, a = b + 10, a, b = a + 1);//此处为逗号表达式
int c = a > b, a = b + 10, a, b = a + 1;//此处为有问题表达式,a和b都重定义了
//此条代码的实质为下:
int c=a >b;
int a=b + 10;//前面已经定义a了,还定义一次所以导致重定义行为
int a;
int b=a + 1;//前面已经定义b了,海淀一一次所以导致重定义行为
//代码2
if (a =b + 1, c=a / 2, d > 0)
//代码3
a = get_val();
count_val(a);
while (a > 0)
{//业务处理a = get_val();count_val(a);
}
//循环前需要执行一段表达式,循环体也需要执行该段表达式
//符合逗号表达式原则,因此可以在循环条件前加该段表达式
如果使⽤逗号表达式,改写:
while (a = get_val(), count_val(a), a>0)
{//业务处理
}总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!
相关文章:

C语言第十五弹---操作符(上)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 操作符 1、操作符的分类 2、二进制和进制转换 2.1、2进制转10进制 2.1.1、10进制转2进制数字 2.2、2进制转8进制和16进制 2.2.2、2进制转16进制 3. 原码、反…...
使用宝塔面板访问MySQL数据库
文章目录 前言一、安装访问工具二、查看数据库总结 前言 前面我们已经部署了前后端项目,但是却不能得到数据库的信息,看有谁再使用你的项目。例如员工、用户等等。本次博客进行讲解如何在宝塔面板里面访问MySQL数据库。 一、安装访问工具 1、打开软件商…...
Win10 双网卡实现同时上内外网
因为需要同时上内网和外网,但公司做了网络隔离,不能同时上内外网,所以多加了块无线网卡,配置双网关实现同时上内外网,互不影响 打开 Windows PowerShell(管理员),输入:ro…...

Django模型(六)
一、其它查询 文档:https://docs.djangoproject.com/zh-hans/4.1/ref/models/querysets/#count 1.1、排序 Queryset.order_by(*fields) 默认情况下,QuerySet 返回的结果是按照模型 Meta 中的 ordering 选项给出的排序元组排序的 可以通过使用 order_by 方法在每个 QueryS…...

【Linux】Linux基本指令
目录 1.ls指令 2.cd指令 3.touch指令 4.mkdir指令 5.rmdir指令和rm指令 5.1rmdir指令 5.2rm指令 6.man指令 7.cp指令 8.mv指令 9.cat指令 10.more指令 && less指令 10.1more指令 10.2less指令 11.head指令 && tail指令 11.1head指令 11.2tai…...

stm32中的SPI
SPI的简介 文章目录 SPI的简介物理层协议层基本通讯过程起始和终止信号数据有效性CPOL/CPHA及通讯模式 STM3的SPI特性及架构通讯引脚时钟控制逻辑数据控制逻辑整体控制逻辑通讯过程 代码配置实现指令集结构体的定义SPI时钟信号的定义SPI端口定义SPI命令 flash驱动代码初始化代码…...
ChatGPT可与自定义GPTs一起使用,智能AI代理时代来啦!
1月31日凌晨,OpenAI在社交平台公布了一个超强新功能,可以在ChatGPT中输入“GPTs名字”的方法,调用多个自定义GPTs一起协同工作。 例如,我想开发一款社交APP,1)可以先用专业分析GPTs做一下市场调研…...

《Numpy 简易速速上手小册》第1章:Numpy 基础(2024 最新版)
文章目录 1.1 创建和操作 Numpy 数组1.1.1 基础知识1.1.2 完整案例:多维数据分析1.1.3 拓展案例 1:时间序列数据1.1.4 拓展案例 2:图像数据处理 1.2 数组的索引和切片1.2.1 基础知识1.2.2 完整案例:时间序列分析1.2.3 拓展案例 1&…...
)
【美团】SaaS技术部-后端研发工程师(海外业务)
部门介绍 美团餐饮系统为餐饮企业提供一站式IT解决方案,帮助餐饮商户实现从供应链管理、生产管理、前厅管理到外卖的数字化经营。美团餐饮系统不仅打通了餐厅和平台,更帮助餐厅连接客人,让商户更了解顾客需求,在帮助商户做商业决…...

linux安装mongodb数据库启动报错? 都是冰红茶滴水儿
先展示报错信息 网上一大推说是关闭不正确导致的,然后给出的解决方法是 ./mongod -f mongodb.conf --repair吊用没有,还是报错: about to fork child process, waiting until server is ready for connections. forked process: 302226 ERROR: child process failed, exited…...

win11安装wsl作为linux子系统并当作服务器
wsl安装 打开控制面板,找到启用或关闭windows功能 开启windows虚拟机监控平台和适用于Linux的Windows子系统,重启电脑。 打开microsoft store搜索ubuntu,找到合适的版本下载安装 输入wsl -l如下所示,即为安装成功。 安装过程比较…...

户用光伏电站的管理包括哪些内容?需要怎么做?
户用光伏电站在运行后需要进行一系列的管理工作,包括安全、运行、质量和数据等等,从而保证电站的安全、经济、高效运行。 1.安全管理 光伏电站的安全管理是非常重要的,包括电站的防雷、防火、防盗等措施,以及电站内部的安全管理…...
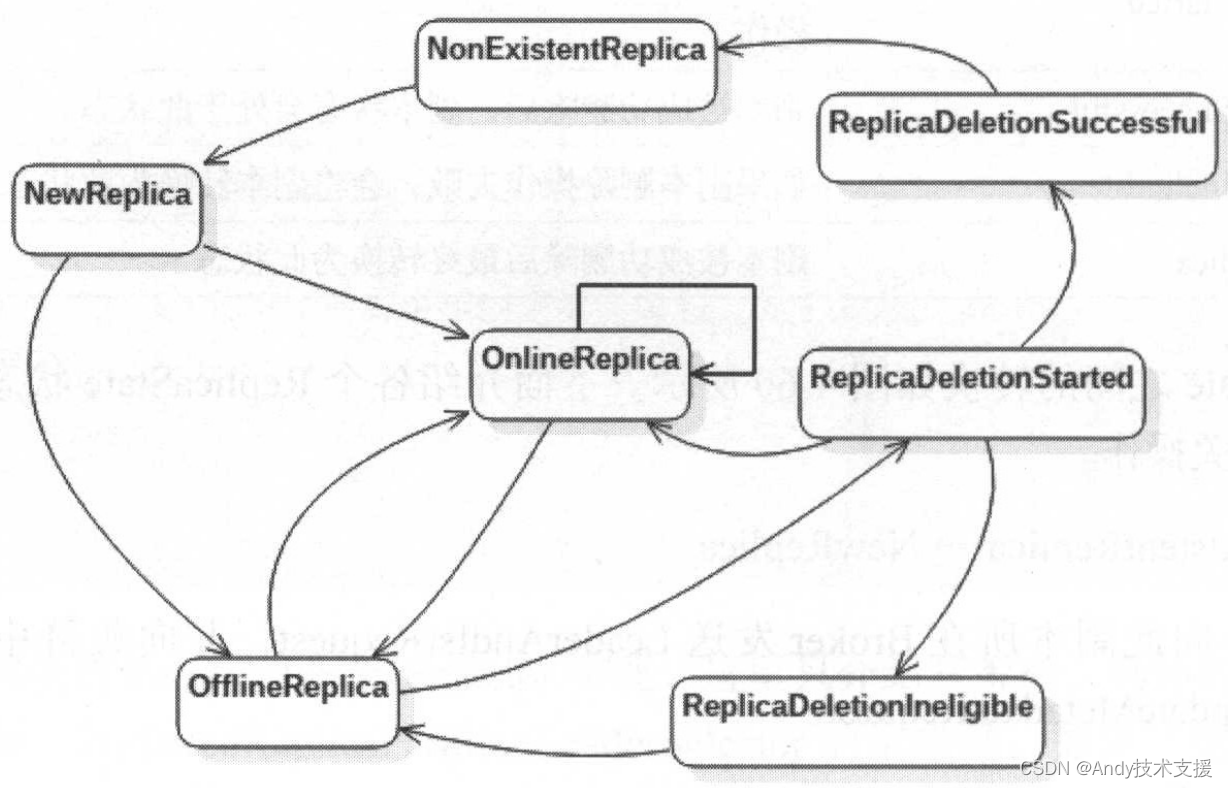
Kafka-服务端-PartitionLeaderSelector、ReplicaStateMachine
PartitionLeaderSelector 通过对前面的分析可知,PartitionMachine将Leader副本选举、确定ISR集合的工作委托给了PartitionLeaderSelector接口实现,PartitionMachine可以专注于管理分区状态。这是策略模式的一种典型的应用场景。 图展示了PartitionLead…...
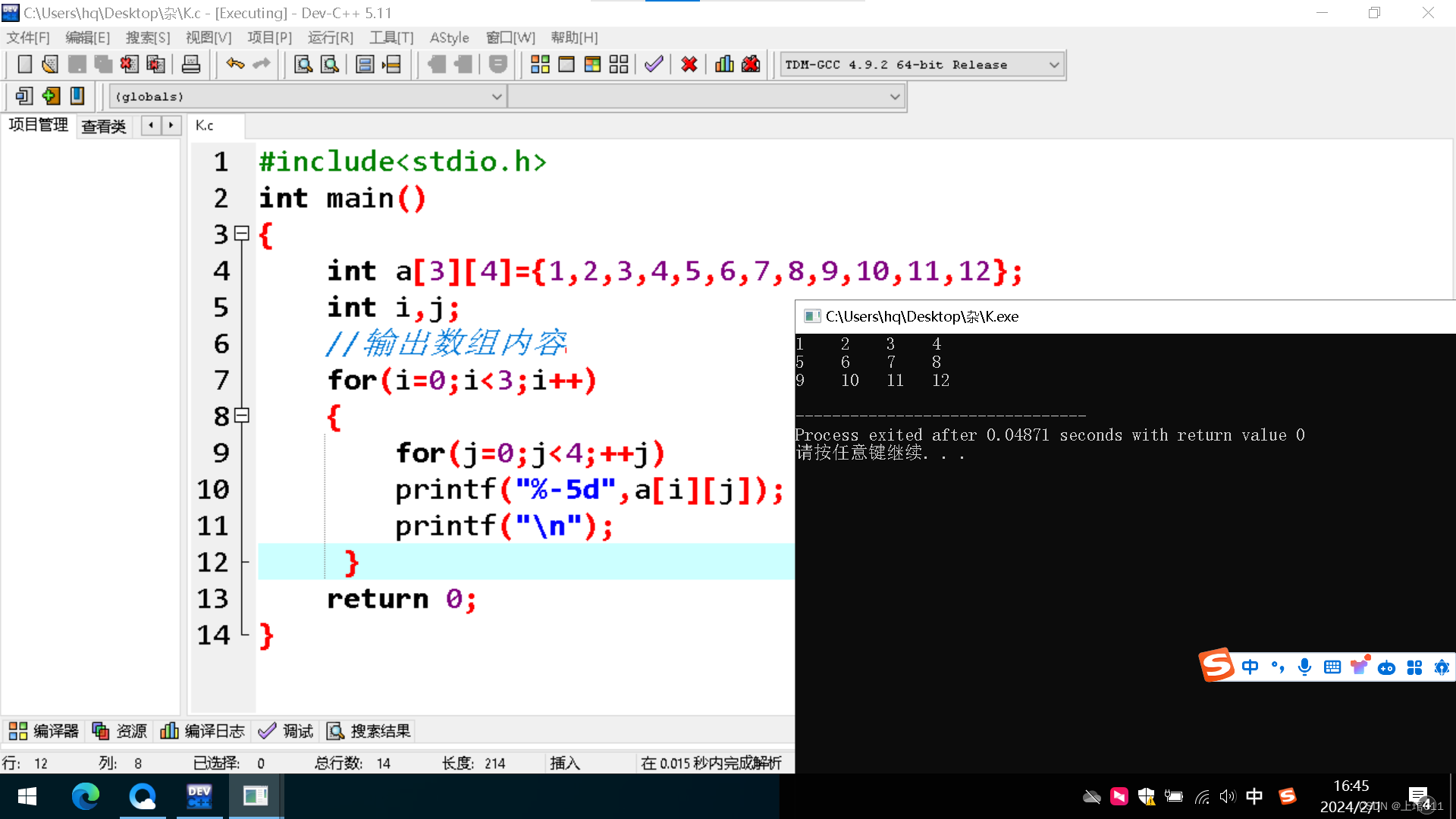
总结11(数组)
数组 1.为什么需要数组 为了解决大量同类型数据的存储和使用问题 为了模拟现实世界 2. 数组的分类 一维数组 1).怎样定义一维数组 为n个变量连续分配存储空间。 所有的变量数据类型必须相同。 所有变量所占的字节大小必须相等。 例子: int a[5]; &#x…...

扩展学习|大数据分析整合到价值创造的大见解
文献来源:Saggi M K, Jain S. A survey towards an integration of big data analytics to big insights for value-creation[J]. Information Processing & Management, 2018, 54(5): 758-790. 下载链接:链接:https://pan.baidu.com/s/14IGaCOc-plxAiaVhwOgUvA 提取码…...
蓝桥杯---牌型种数
小明被劫持到X赌城,被迫与其他3人玩牌。一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。这时,小明脑子里突然冒出一个问题:如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后…...

【Linux】VMware Workstation16安装银河麒麟高级服务器操作系统V10 SP3 AMD64
目录 一、麒麟服务器概述 二、安装步骤 设置硬盘大小 完成配置 修改内存 处理器等设备配置 选择直接安装 配置磁盘 网络配置 设置root账号密码 开始安装 启动完成 一、麒麟服务器概述 银河麒麟高级服务器操作系统V10是针对企业级关键业务,适应虚拟化、云…...

中国的茶文化:历史、传统与生活
中国的茶文化:历史、传统与生活 一、引言 茶,这一神奇而古老的饮品,与中国的历史、文化和生活方式紧密相连。中国的茶文化,源远流长,博大精深,是中华文明的重要组成部分。它不仅是一种饮料,更是…...

Oracle函数使用
ROW_NUMBER函数 ROW_NUMBER() OVER(PARTITION BY column1 ORDER BY column2 DESC) -- 根据column1分组按column2降序排序生成序号,序号由小到大,会生成一个唯一的序号 -- 例如column2中有两列值都为1,那他们的序号会有一个在上一个在下ROW_NUMBER() OVER(ORDER BY …...

正则表达式与文本三剑客
目录 一、正则表达式 1. 定义 2. 字符匹配 3. 重复限定符 4. 位置锚点 5. 分组和引用 6. 扩展正则表达式 二、文本三剑客 1. grep 1.1 定义 1.2 语法 1.3 选项 1.4 示例 2. sed 2.1 定义 2.2 通式 2.3 选项 2.4 脚本格式(脚本语法) 2.…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
