代码随想录算法训练营第三十七天 | 738.单调递增的数字、 968.监控二叉树
题目链接:738.单调递增的数字
文章讲解:代码随想录 738.单调递增的数字讲解
视频讲解:贪心算法,思路不难想,但代码不好写!LeetCode:738.单调自增的数字
思路和解法
题目:
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
想法:
关键思想在于从后向前遍历,遇到需要改的地方后面都需要改为9,所以就只记录最前面需要改的地方即可。
class Solution {
public://整体思路:从后向前遍历字符,如果i-1 < i那么i位置的要改为9,i-1位置的要减1//注意:一个位置改为了9,后面的位置都要改为9,所以只要记录第一个需要改为9的位置即可int monotoneIncreasingDigits(int n) {string s = to_string(n);//这里必须要初始化,防止在不需要任何改动时。不知道初始化值还是给改动了,所以初始化为一个不可能进行改动值int flag = s.size();for (int i = s.size() - 1; i > 0; i--) {if (s[i - 1] > s[i]) {//flag前一个位置-1,这个不能写在外面,否则不需要更改时也会把最后一位修改掉s[i - 1]--;flag = i;}}//进行修改,把flag以后的数字都改为9for (int i = flag; i < s.size(); i++) {s[i] = '9';}return stoi(s);}
};
题目链接:968.监控二叉树
文章讲解:代码随想录 968.监控二叉树讲解
视频讲解:贪心算法,二叉树与贪心的结合,有点难… LeetCode:968.监督二叉树
思路和解法
题目:
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
想法:
关键思想在于后序遍历二叉树,通过子节点的状态来判断当前节点的状态。还有比较难想的就是怎么划分状态,还有对每种状态的处理方式,直接看讲解还是比较符合思维习惯的,但是自己想不好想,还有最后对根节点无覆盖的处理非常容易忽视,遇到报错有可能会发现。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://整体思路:为了尽可能少用摄像头,从下往上遍历二叉树,并把每个节点分为三种状态:0:无覆盖 1:有摄像头 2:有覆盖//对当前节点进行处理需要知道子节点的情况,因此递归函数有返回值,返回值就是当前节点的状态,而且还要后序遍历//当子节点中至少有一个无覆盖时,当前节点要设置摄像头;//剩下的情况不包含无覆盖,子节点至少有一个摄像头时,当前节点设置为有覆盖,子节点均为有覆盖时,当前节点设置为无覆盖//问题:空节点如何设置(返回什么)?空节点是不需要处理的节点,同时为了少用摄像头,希望空节点的父节点不要设置摄像头,所以不能将空节点设置为无覆盖//空节点的父节点其实是无覆盖,所以将空节点设置为有覆盖,这样其父节点的状态就会由零一个子节点决定//注意:遍历过程中遇到设置摄像头,记录摄像头结果数+1//记录摄像头数量int result = 0;//递归函数int traversal(TreeNode* node) {//终止条件:遇到了空节点if (node == nullptr) {return 2;}int left = traversal(node -> left);int right = traversal(node -> right);if (left == 0 || right == 0) {result++;return 1;} else if (left == 1 || right == 1) {return 2;} else {return 0;}}int minCameraCover(TreeNode* root) {int tmp = traversal(root);//注意:tmp接到的是root的状态,如果root状态是0,就还需要一个摄像头放在root上if (tmp == 0) result++;return result;}
};
相关文章:

代码随想录算法训练营第三十七天 | 738.单调递增的数字、 968.监控二叉树
题目链接:738.单调递增的数字 文章讲解:代码随想录 738.单调递增的数字讲解 视频讲解:贪心算法,思路不难想,但代码不好写!LeetCode:738.单调自增的数字 思路和解法 题目: 当且仅当每个相邻位…...

【Django-ninja】django-ninja的hello world
django-ninja简介 Django Ninja是一个用于使用Django和Python 3.6类型提示构建API的Web框架。 主要特点: 易用性:旨在易于使用和直观。 高性能执行:由于Pydantic和异步支持,具有非常高的性能。 编码效率高:类型提…...
ArrayList集合初始化长度是多少,初始化的时候分配内存空间吗
ArrayList一旦初始化,在内存中就会分配空间吗 是的,当ArrayList在Java中初始化时,即使它没有添加任何元素,也会立即分配内存空间。具体来说,对于默认构造函数创建的ArrayList(即不指定初始容量)…...

C语言数组:从入门到进阶
前言: 在这篇博客中,我们将学习如何使用C语言数组的基本知识。数组是C语言中的一种重要数据结构,它允许我们存储一系列相同类型的数据。我们将讨论数组的定义、初始化、访问元素、遍历数组以及数组的应用场景。此外,我们还将通过…...

9.回文数
回文数 将整型转换为字符型反转前一半是否等于后一半将数字本身反转输入一个整数 x,如果 x是一个回文整数,返回 true;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。 例如,121 是回文,而 123 不是。 将整型转换为字符型 反转…...

一分钟在SpringBoot项目中使用EMQ
先展示最终的结果: 生产者端: RestController RequiredArgsConstructor public class TestController {private final MqttProducer mqttProducer;GetMapping("/test")public String test() {User build User.builder().age(100).sex(1).address("世界潍坊渤…...

SOME/IP 协议介绍(七)传输 CAN 和 FlexRay 帧
SOME/IP 不应仅用于传输 CAN 或 FlexRay 帧。但是,消息 ID 空间需要在两种用例之间进行协调。 传输 CAN/FlexRay 应使用完整的 SOME/IP 标头。 AUTOSAR Socket-Adapter 使用消息 ID 和长度来构建所需的内部 PDU,但不会查看其他字段。因此,必…...
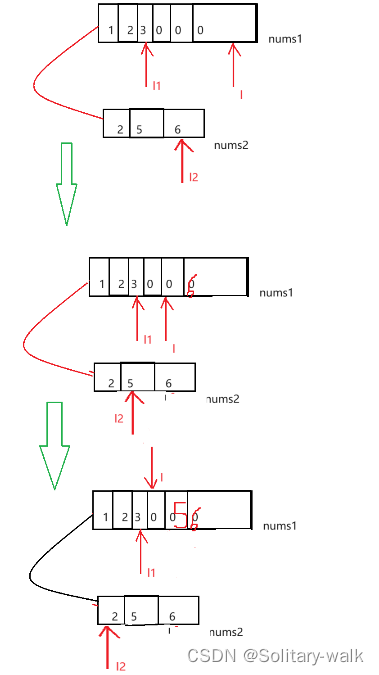
与数组相关经典面试题
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary-walk ⸝⋆ ━━━┓ - 个性标签 - :来于“云”的“羽球人”。…...

数据结构与算法面试系列-02
1. 一个整数,它加上100后是一个完全平方数,加上168又是一个完全平方数,请问该数是多少? 程序分析:在10万以内判断,先将该数加上100后再开方,再将该数加上168后再开方,如果开方后的结果满足如下条件,即是结果。请看具体分析: 程序代码如下: package com.yoodb.uti…...
CMake 完整入门教程(五)
CMake 使用实例 13.1 例子一 一个经典的 C 程序,如何用 cmake 来进行构建程序呢? //main.c #include <stdio.h> int main() { printf("Hello World!/n"); return 0; } 编写一个 CMakeList.txt 文件 ( 可看做 cmake 的…...

pgsql中with子句和直接查询差别
1、代码的可读性和维护性: 当查询较为复杂时,WITH子句可以将复杂的查询分解成多个简单的步骤,每个步骤都可以有一个易于理解的名字。这样做提高了代码的可读性,也便于后期维护。 2、代码的重用性: 在WITH子句中定义…...

Day 31 | 贪心算法 理论基础 、455.分发饼干 、 376. 摆动序列 、 53. 最大子序和
理论基础 文章讲解 455.分发饼干 题目 文章讲解 视频讲解 思路:从小饼干开始喂小胃口 class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int start 0;int count 0;for (int i 0; i < s.length &&a…...

vue3使用is动态切换组件报错Vue received a Component which was made a reactive object.
vue3使用is动态切换组件,activeComponent用ref定义报错 Vue received a Component which was made a reactive object. This can lead to unnecessary performance overhead, and should be avoided by marking the component with markRaw or using shallowRef ins…...
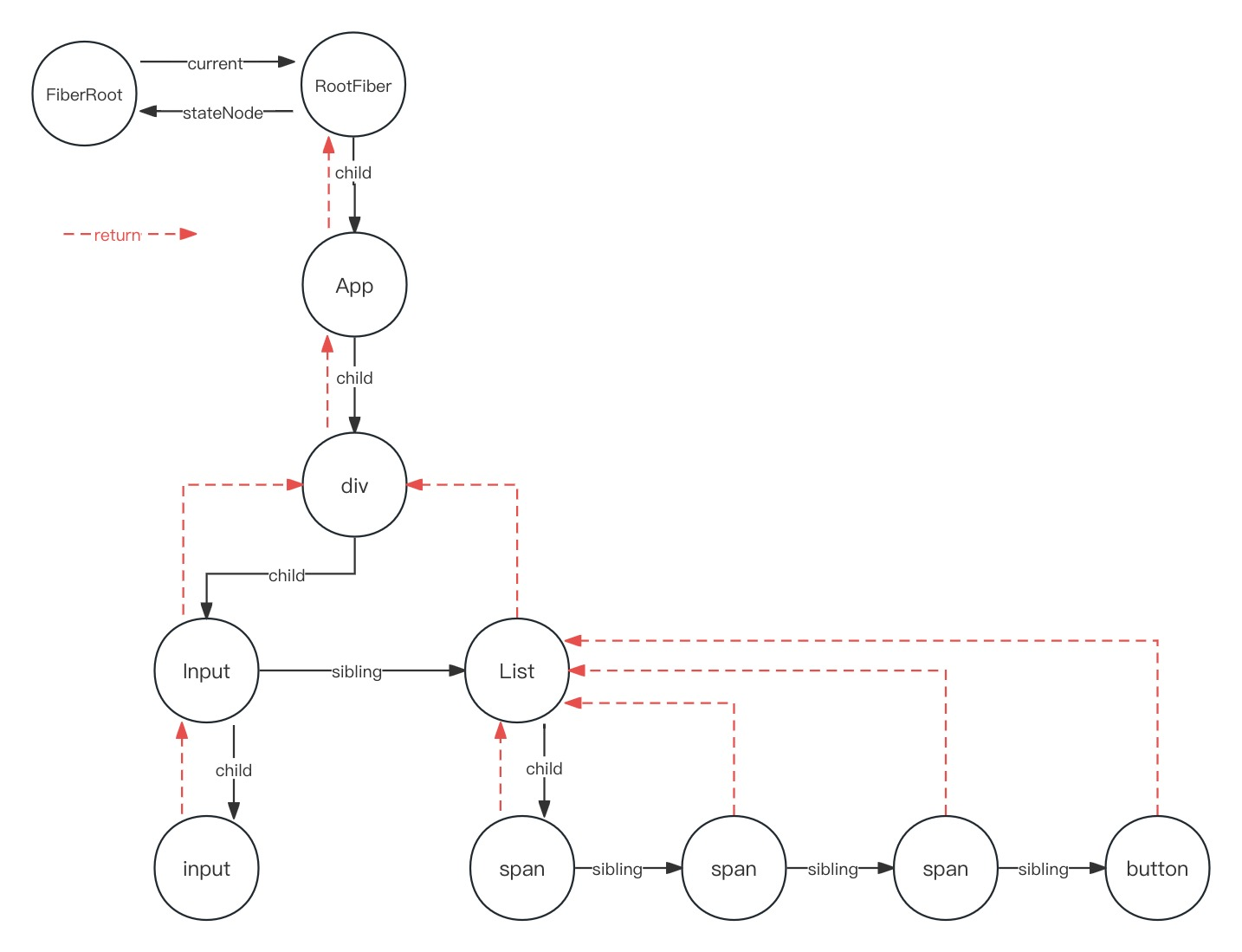
React16源码: React中LegacyContext的源码实现
LegacyContext 老的 contextAPI 也就是我们使用 childContextTypes 这种声明方式来从父节点为它的子树提供 context 内容的这么一种方式遗留的contextAPI 在 react 17 被彻底移除了,就无法使用了那么为什么要彻底移除这个contextAPI的使用方式呢?因为它…...
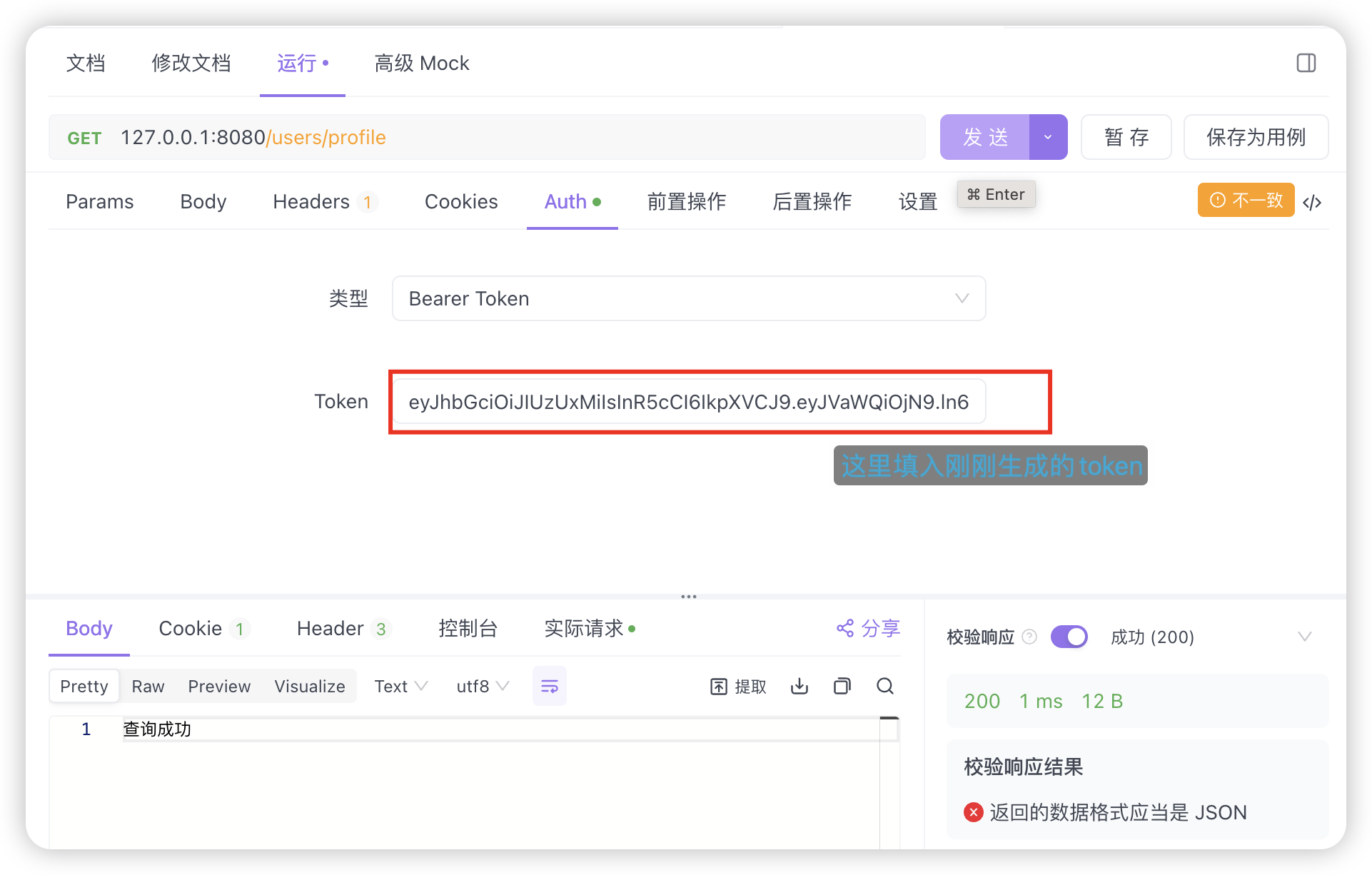
Gin 框架之jwt 介绍与基本使用
文章目录 一.JWT 介绍二.JWT认证与session认证的区别2.1 基于session认证流程图2.2 基于jwt认证流程图 三. JWT 的构成3.1 header : 头部3.2 payload : 负载3.2.1 标准中注册的声明 (建议但不强制使用)3.2.2 公共的声明3.2.3 私有的声明3.2.4 定义一个payload 3.3 signatrue : …...
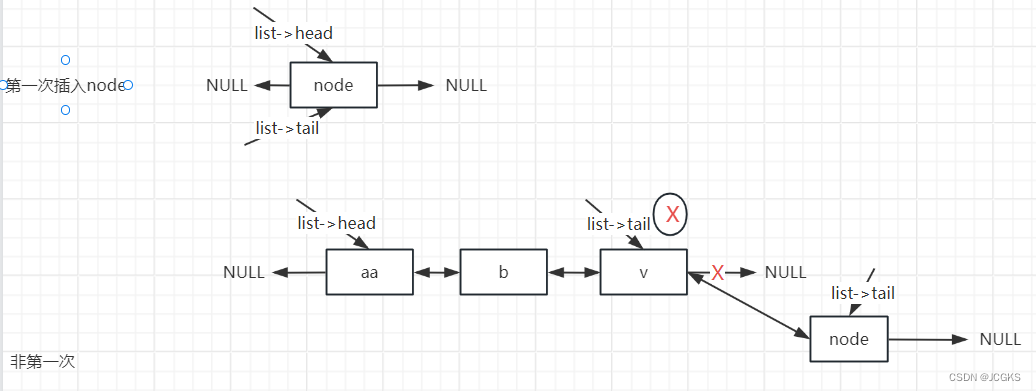
从[redis:LinkedList]中学习链表
文章目录 adlistlistNodelistmacros[宏定义]listCreatelistInitNodelistEmptylistReleaselistAddNodeHeadlistLinkNodeHeadlistAddNodeTaillistLinkNodeTaillistInsertNodelistDelNodelistUlinkNodelistIndexredis3.2.100quicklistredis7.2.2quicklist redis的基本数据类型之一…...
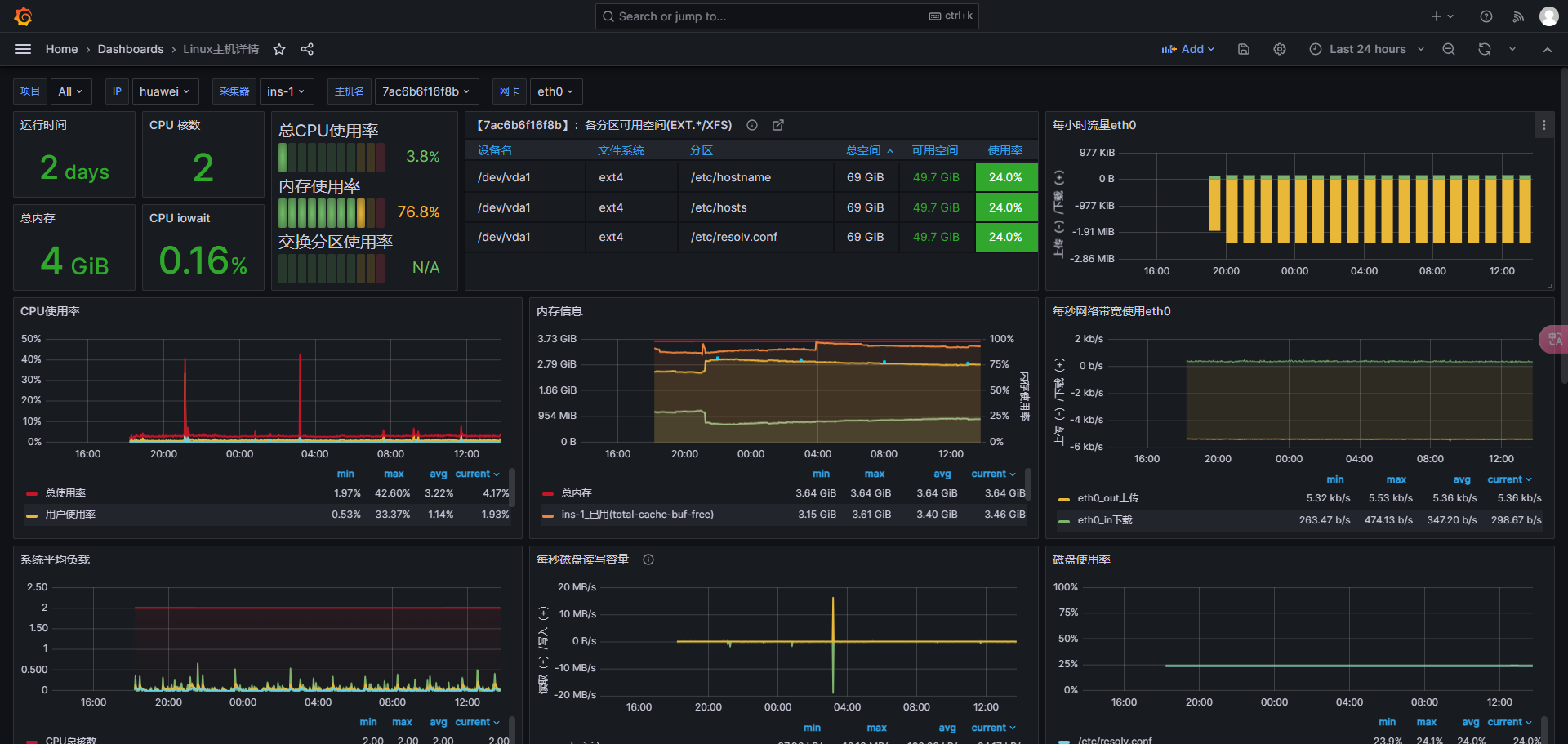
Prometheus+grafana配置监控系统
使用docker compose安装 方便拓展, 配置信息都放在在 /docker/prometheus 目录下 1.目录结构如下 . ├── conf │ └── prometheus.yml ├── grafana_data ├── prometheus_data └── prometheus_grafana.yaml2.创建目录文件 mkdir /docker/prometheus &&am…...
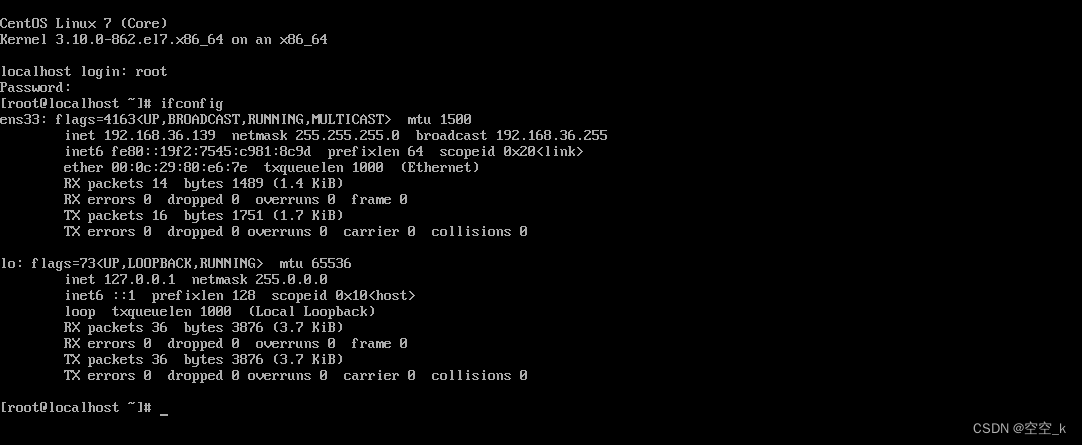
Linux之安装配置CentOS 7
一、CentOS简介 CentOS(Community Enterprise Operating System,中文意思是社区企业操作系统)是Linux发行版之一,它是来自于Red Hat Enterprise Linux依照开放源代码规定释出的源代码所编译而成。由于出自同样的源代码,…...
神经网络与深度学习Pytorch版 Softmax回归 笔记
Softmax回归 目录 Softmax回归 1. 独热编码 2. Softmax回归的网络架构是一个单层的全连接神经网络。 3. Softmax回归模型概述及其在多分类问题中的应用 4. Softmax运算在多分类问题中的应用及其数学原理 5. 小批量样本分类的矢量计算表达式 6. 交叉熵损失函数 7. 模型预…...

git学习及简单maven打包
前提: 已经有远程仓库地址 和账号密码了 已经安装git了 1.本地新建文件夹A用作本地仓库 2.在A文件夹下右键打开GIT BASH HERE 3.创建用户和密码,方便追踪提交记录 git config --global user.email “caoqingqing0108” //创建邮箱 git config --global …...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
