数据结构-内部排序
简介
排序(Sorting):将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列
排序算法分为内部排序和外部排序
内部排序:在排序期间数据对象全部存放在内存的排序
外部排序:在排序期间全部对象个数太多,不能同时存放在内存,必须根据排序过程的要求,不断在内、外存之间移动的排序
排序方法的稳定性:
如果在记录序列中有两个记录r[i]和r[j], 它们的关键字key[i]==key[j]且在排序之前, 记录r[i]排在r[j]前面。
如果在排序之后, 记录r[i]仍在记录r[j]的前面, 则称这个排序方法是稳定的, 否则称这个排序方法是不稳定的
排序常用的数据结构是数组、顺序表、结构体
排序算法的应用非常广泛,商业领域、生活领域、科研领域都几乎离不开排序
淘宝商品价格排序(海量数据排序)
微博热搜排行榜(点击量动态排序)
QQ好友列表(字符排序)
数列相似度(将数列元素排序后对比)
元素唯一性(排序后找出重复项)
凸包问题(例如图像识别手势,采点绘制轮廓)
排序介绍
排序包含两种基本操作
比较:比较两个关键字的大小
移动:将记录从一个位置移动至另一个位置
排序算法的时间复杂度,用算法执行中的记录关键字比较次数与记录移动次数来衡量
根据排序思想来划分,内部排序算法分为五类
插入排序:直接插入排序、希尔排序
交换排序:冒泡排序、快速排序
选择排序:简单选择排序、堆排序
归并排序:两路归并排序
基数排序:k进制位数排序
判断排序好坏的方法
算法的时间复杂度、空间复杂度
算法的稳定性
排序算法的最好情况(比较和移动次数最少)
排序算法的最坏情况(比较和移动次数最多)
初始待排序序列是否会影响排序算法性能
排序次数是否固定
每一趟排序能否确定一个元素的最终排序位置
插入排序
插入排序的思想:假设前k-1个记录已经排序,第k个元素找到合适位置插入。分为
直接插入排序
希尔排序
直接插入排序
1. 直接插入排序是最简单的排序方法,操作:
每步将一个待排序的对象,按其关键字大小,插入到前面已经排好序的有序表的适当位置上, 直到对象全部插入为止
2. 直接插入排序的算法步骤:
当插入第i(i≥1)个对象时, 前面的r[0], r[1], …, r[i-1]已经排好序。
用r[i]的关键字与r[i-1], r[i-2], …的关键字顺序进行比较(和顺序查找类似),如果小于,则将r[x]向后移动(插入位置后的记录向后顺移)
找到插入位置即将r[i]插入
3. 直接插入排序的算法分析
直接插入排序的时间复杂度为O(n2),空间复杂度O(1)
直接插入排序是一种稳定的排序方法
直接插入排序最大的优点是简单,在记录数较少时,是比较好的办法
4.其他
算法性能与关键字的初始排列有关,成正比关系。初始排列越有序,比较和移动次数越少
最好情况,排序前已经有序,总比较次数n-1,移动次数0
最坏情况,排序前是逆序,每趟排序都要比较i-1次和移动i-1次,总比较次数n2/2,总移动次数n2/2
每趟排序不能确定一个元素的最终排序位置,例如最后一个元素是最小值插入到第一个元素位置,导致前n-1个元素都要后移
//直插排序
/*
因为直接插入排序过程中,前i-1个元素是有序的,所以可以改进为折半插入排序
折半插入排序是指在查找记录插入位置时,采用折半查找算法,折半查找比顺序查找快,所以折半插入排序在查找上性能比直接插入排序好
由于需要移动的记录数目与直接插入排序相同(为O(n2)),所以折半插入排序的时间复杂度为O(n2)
*/
void insert(int *a)
{for(int i=1;i<l;i++){int tmp=a[i];int j=i;while(j>0){if(a[j-1]<tmp)break;a[j]=a[j-1];j--;}a[j]=tmp;}
}
希尔排序
1.希尔排序的思想:先将待排序列分成若干子序列;对其分别进行插入排序;待整个序列基本有序时,再对全体记录进行一次直接插入排序,希尔排序(Shell Sort)又称为缩小增量排序
2. 希尔排序的算法设计
首先取一个整数 gap < n(待排序记录数) 作为间隔, 将全部记录分为 gap 个子序列, 所有距离为 gap 的记录放在同一个子序列中
在每一个子序列中分别施行直接插入排序。
然后缩小间隔 gap, 例如取 gap = gap/2
重复上述的子序列划分和排序工作,直到最后取gap = 1, 将所有记录放在同一个序列中排序为止。
3. 排序举例
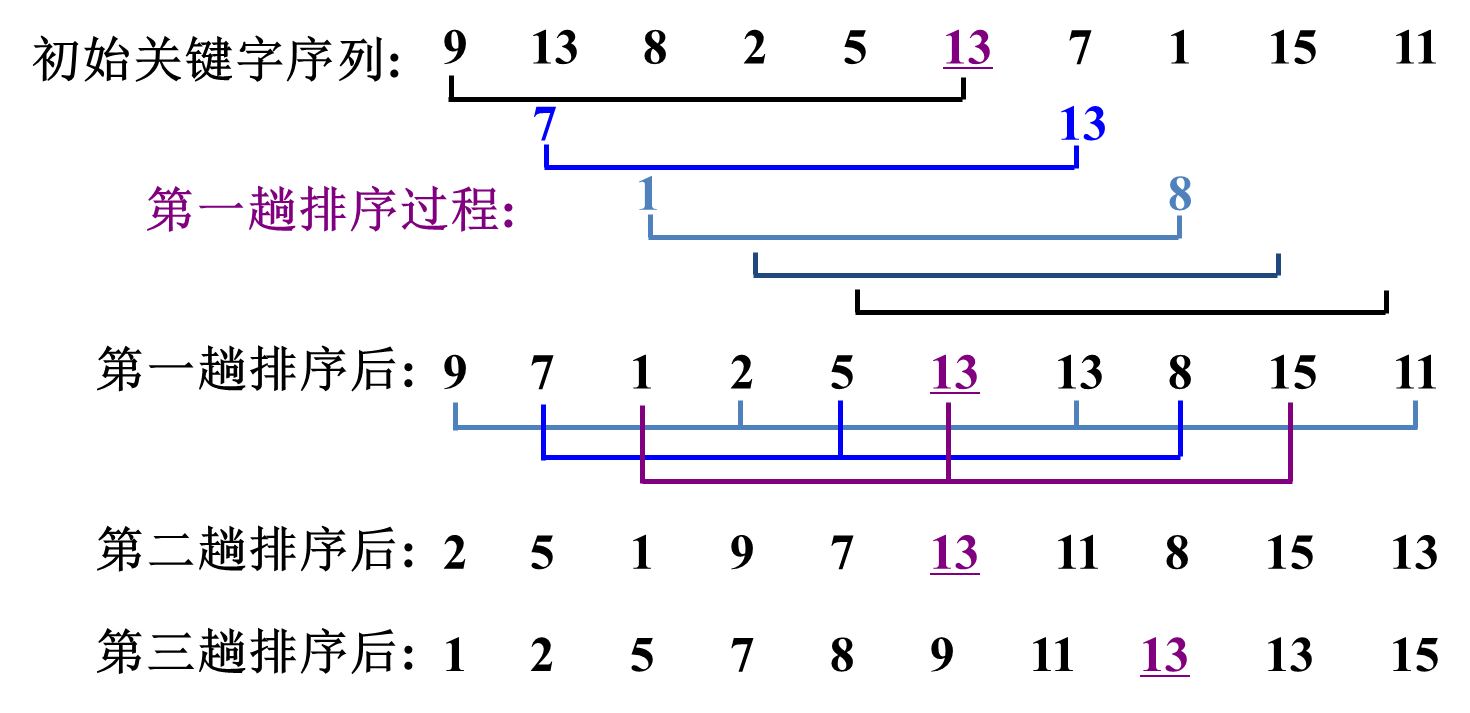
4. 希尔排序的算法分析
开始时,gap的值较大,子序列中的记录较少,排序速度较快
随着排序进展,gap值逐渐变小,子序列中记录个数逐渐变多,由于前面大多数记录已基本有序, 所以排序速度仍然很快。
gap的取法有多种,一般取法:gap=n/2,gap=gap/2,直到gap = 1
代码实现
//希尔排序
/*
希尔排序的算法分析
希尔排序所需的比较次数和移动次数约为n1.3
当n趋于无穷时可减少到n×(log2n)2
希尔排序的时间复杂度约为O(n(log2n)2)
希尔排序是一种不稳定的排序方法
*/
void Xier(int *a)
{int gap = l / 2;while (gap >=1) {for (int i = 0; i <l-gap; i++) {for (int j = i; j < l; j += gap) {if (a[i] > a[j ])swap(a[i], a[j]);}}gap /= 2;show(a);}
}
交换排序
交换排序的思想:比较序列中前后两个位置的元素,如果符合前小后大或前大后小,则继续比较;如果不符合则交换两个位置的元素,再继续比较。
交换排序的算法有:起泡排序 快速排序
起泡排序
1. 起泡排序,又称冒泡排序,算法思想:
设待排序记录序列中的记录个数为n
一般地,第i趟排序从1到n-i+1
依次比较相邻两个记录的关键字,如果发生逆序,则交换之
其结果是这n-i+1个记录中,关键字最大的记录被交换到第n-i+1的位置上,最多作n-1趟。
2. 冒泡排序的算法过程
i=1,为第一趟排序,关键字最大的记录将被交换到最后一个位置
i=2,为第二趟排序,关键字次大的记录将被交换到最后第二个位置
依此类推……
关键字小的记录不断上浮(起泡),关键字大的记录不断下沉(每趟排序最大的一直沉到底)
3.冒泡排序举例
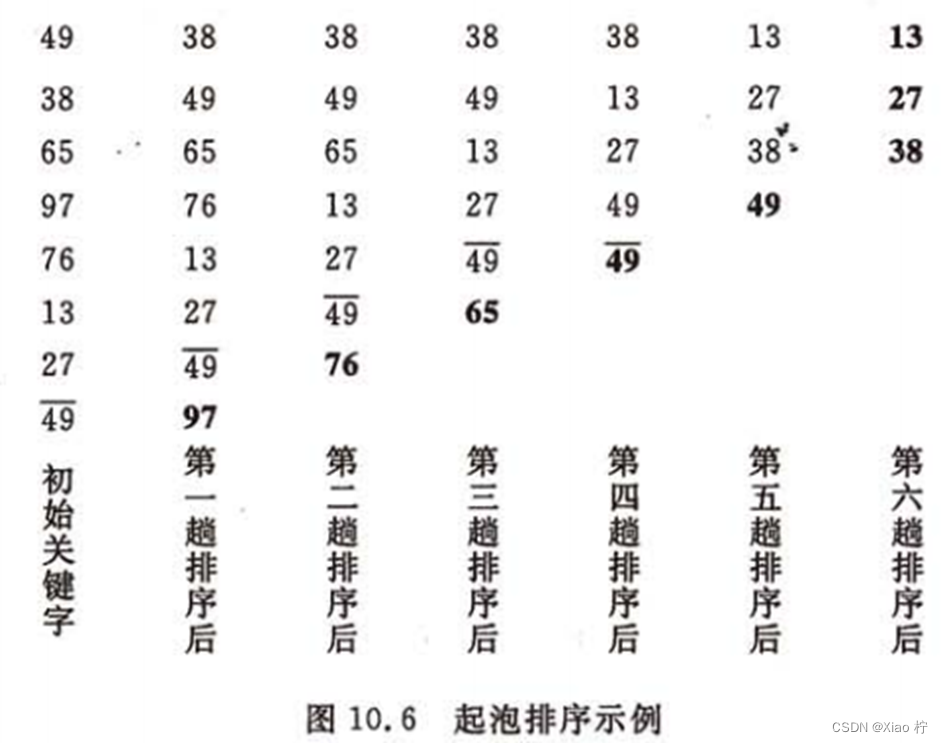
4. 冒泡排序的算法分析
起泡排序的时间复杂度为O(n2),空间复杂度O(1)
起泡排序是一种稳定的排序方法
5. 冒泡排序的其他分析
算法性能与关键字的初始排列有关,成正比关系。初始排列越有序,比较和移动次数越少
最好情况,排序前已经有序,只执行一趟,总比较次数n-1,移动次数0
最坏情况,排序前是逆序,每趟排序都要比较i-1次和移动i-1次,总比较次数n2/2,总移动次数n2/2
冒泡排序能够提前结束,最好情况下只要一趟比较就结束。
每趟排序能够确定一个元素的最终排序位置,因为每一趟排序会把最大或最小元素排到末尾,不再参与排序
代码实现
//冒泡排序
void maopao(int *a)
{for (int i = 0; i <l; i++) {for (int j = 0; j < l - i-1; j++) {if (a[j] >= a[j + 1]) {swap(a[j], a[j + 1]);}}}
}
快速排序
1.快速排序算法设计:
任取待排序记录序列中的某个记录(例如取第一个记录)作为基准(枢),按照该记录的关键字大小,将整个记录序列划分为左右两个子序列:
左侧子序列中所有记录的关键字都小于或等于基准记录的关键字
右侧子序列中所有记录的关键字都大于基准记录的关键字
基准记录则排在这两个子序列中间(这也是该记录最终应安放的位置)
然后分别对这两个子序列重复施行上述方法,直到所有的记录都排在相应位置上为止。
基准记录也称为枢轴(或支点)记录。
2. 快速排序算法过程
取序列第一个记录为枢轴记录,其关键字为Pivotkey
指针low指向序列第一个记录位置
指针high指向序列最后一个记录位置
一趟排序(某个子序列)过程
①.从high指向的记录开始,向前找到第一个关键字的值小于Pivotkey的记录,将其放到low指向的位置,low+1
②.从low指向的记录开始,向后找到第一个关键字的值大于Pivotkey的记录,将其放到high指向的位置,high-1
③.重复1,2,直到low=high,将枢轴记录放在low(high)指向的位置
对枢轴记录前后两个子序列执行相同的操作,直到每个子序列都只有一个记录为止
3. 快速排序的算法分析
快速排序是一个递归过程, 其递归树如图所示,利用序列第一个记录作为基准,将整个序列划分为左右两个子序列。只要是关键字小于基准记录关键字的记录都移到序列左侧
可证明快速排序的平均计算时间是O(nlog2n)
实验结果表明: 就平均计算时间而言, 快速排序是所有内排序方法中最好的一个
但快速排序是一种不稳定的排序方法
代码实现
//快速排序
int getpiot(int *a, int l, int r) {int tmp = a[l];while (l < r) {while (l < r && a[r] >= tmp)r--;swap(a[r], a[l]);while (l < r && a[l] <= tmp)l++;swap(a[l], a[r]);}return l;
}
void quick_sort(int *a,int l,int r)
{if(l>=r)return;int p= getpiot(a,l,r);show(a);quick_sort(a,l,p-1);quick_sort(a,p+1,r);
}
选择排序
选择排序的思想,每一趟选出第i小(大)的元素,与第i个位置的元素交换
选择排序算法包括
简单选择排序
堆排序
简单选择排序
1.简单选择排序的算法设计:
每一趟(例如第i趟,i=1,2,…,n-1)在后面 n-i+1个待排序记录中通过n-i次比较,选出关键字最小的记录,与第i个记录交换
2.简单选择排序的算法分析
时间复杂度O(n2)
是一种不稳定的排序方法
3.其他
简单选择排序的其他分析
简单选择排序性能与记录的初始排列无关。无论是否有序,都要每趟全部扫描找出第i小(大)的元素,第i趟选择的比较次数总是 n-i次
每趟排序能够确定一个元素的最终排序位置,因为每一趟排序后,第i小(大)的元素放在第i个位置
当不需要全部排序,只需要排序出前k个元素,用简单选择排序是一种好的算法。
代码实现
//简单选择排序
void choose(int *a)
{for(int i=0;i<l-1;i++) {int mini = i;for (int j = i + 1; j < l; j++) {if (a[j] < a[mini]) {mini = j;}}if (mini != i)swap(a[i], a[mini]);}
}
堆排序
1. 堆排序算法流程
将初始序列从1至n按顺序创建一个完全二叉树
将完全二叉树调整为堆
最后结点与根结点交换
排除掉最后结点,重复步骤2,直到剩下一个结点
2. 堆排序的算法分析
对长度为n的序列,排序最多需要做n-1次调整建新堆(筛选)。建初始堆时,需要n/2次筛选,因此共需要O(n×k)量级的时间
k=log2n,堆排序时间复杂度为O(nlog2n)
堆排序是一个不稳定的排序方法
代码实现
void HeapAdjust(int* arr, int start, int end)
{int tmp = arr[start];for (int i = 2 * start + 1; i <= end; i = i * 2 + 1){if (i < end&& arr[i] < arr[i + 1])//有右孩子并且左孩子小于右孩子{i++;}//i一定是左右孩子的最大值if (arr[i] > tmp){arr[start] = arr[i];start = i;}else{break;}}arr[start] = tmp;
}
void HeapSort(int* arr)
{//第一次建立大根堆,从后往前依次调整for(int i=(l-1-1)/2;i>=0;i--){HeapAdjust(arr, i, l - 1);}show(arr);//每次将根和待排序的最后一次交换,然后在调整int tmp;for (int i = 0; i < l- 1; i++){tmp = arr[0];arr[0] = arr[l - 1-i];arr[l - 1 - i] = tmp;HeapAdjust(arr, 0, l - 1-i- 1);show(arr);}
}
归并排序
1. 归并排序的思想:将两个或两个以上的有序表合并成一个新的有序表。
两个有序顺序表合并为新的有序表时,借助多一倍空间,使得记录无需移动,直接插入新空间中。
两路归并:将初始序列分成前后两组,通过比较归并到目标序列中
2. 2路归并排序算法设计:
将n个记录看成是n个有序序列
将前后相邻的两个有序序列归并为一个有序序列(两路归并)
重复做两路归并操作,直到只有一个有序序列为止
3. 2路归并排序算法举例
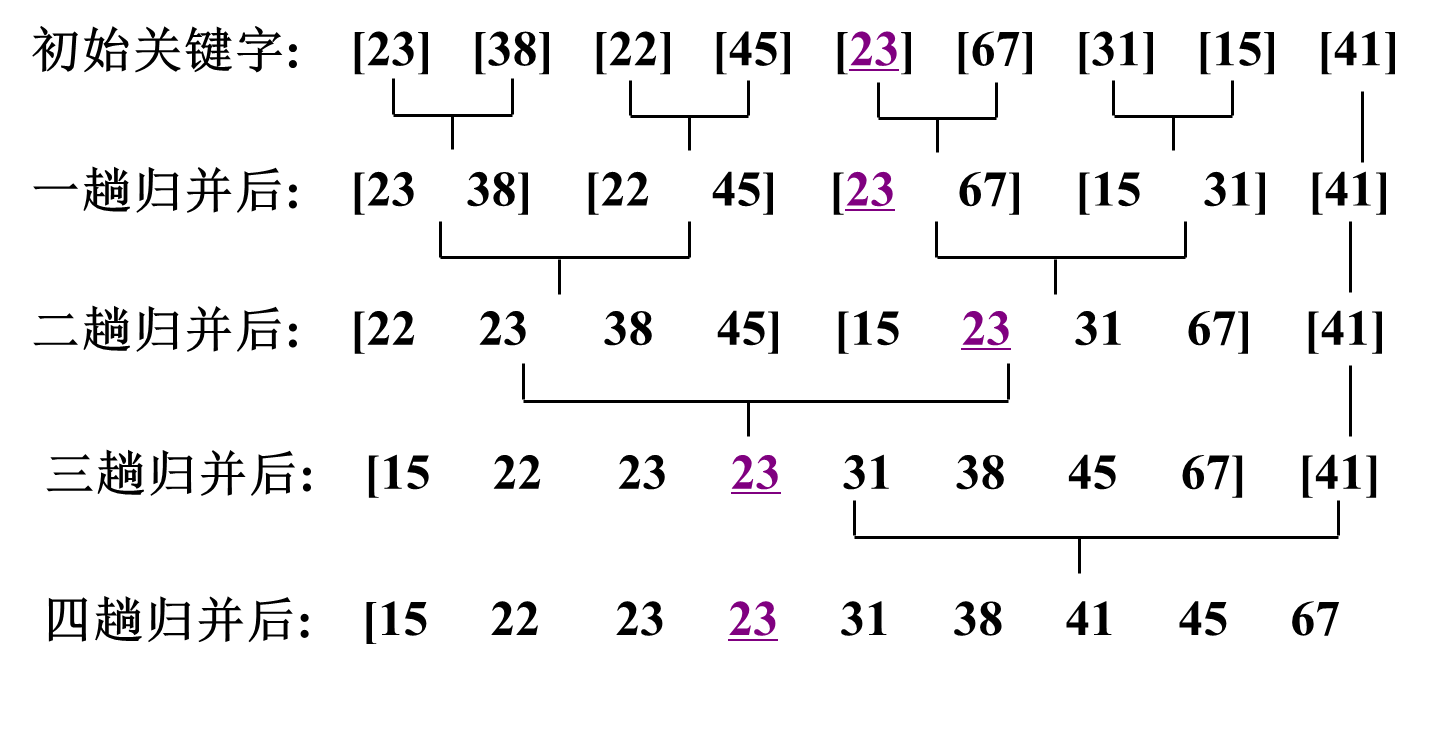
4. 2路归并排序算法分析:
如果待排序的记录为n个,则需要做log2n趟两路归并排序,每趟两路归并排序的时间复杂度为O(n)
2路归并排序的时间复杂度为O(nlog2n)
归并排序的空间复杂度是O(n)
归并排序是一种稳定的排序方法
5. 其他
归并排序优点:时间复杂度为O(nlog2n)且是稳定的排序方法
缺点需要额外空间,归并排序的空间复杂度是O(n)
归并排序性能与记录的初始排列无关。无论是否有序,每趟都要逐个两子序列相互合并,一定要log2n趟
每趟排序不能够确定一个元素的最终排序位置,因为如果最后一个子序列包含最小元素,在最后一趟排序时要插入到最前位置,导致所有元素都要移动
6. 代码实现
可选择递归或非递归实现
//归并排序
void merge(string *a,string *b,int start,int mid,int left)
{int i=start,k=start,j=mid+1;while(i!=mid+1&&j!=left+1){if(a[i]>=a[j])b[k++]=a[i++];elseb[k++]=a[j++];}while(i!=mid+1)b[k++]=a[i++];while(j!=left+1)b[k++]=a[j++];for(i=start;i<=left;i++)a[i]=b[i];
}void merge_sort(string *a,string *b,int start,int end) //递归实现归并排序
{if(start<end){int mid=start+(end-start)/2;merge_sort(a,b,start,mid);merge_sort(a,b,mid+1, end);merge(a,b,start,mid,end);}
}void merge_sort(string *a,string *b) //非递归实现归并排序
{int right,left,mid;for(int i=1;i<l;i=2*i){for(left=0;left<l-1;left+=2*i){mid=left+i-1;if(mid>=l-1)break;right=left+2*i-1;if(right>=l)right=l-1;merge(a,b,left,mid,right);}}
}
基数排序
1. 基数排序:通过“分配”和“收集”若干次操作,对单逻辑关键字进行排序的一种方法。
2. 链式基数排序的算法设计:
基于最低位优先法思想
用链表作存储结构的基数排序
以十进制为例
①.设置10个队列,f[i]和e[i]分别为第i个队列的头指针和尾指针
②.第i趟分配:根据第i位关键字的值,改变记录的指针,将链表中记录按次序分配至10个链队列中(采用队尾插入法);每个队列中记录关键字的第i位关键字相同
③.第i趟收集:改变所有非空队列的队尾记录的指针域,令其指向下一个非空队列的队头记录,重新将10个队列链成一个链表

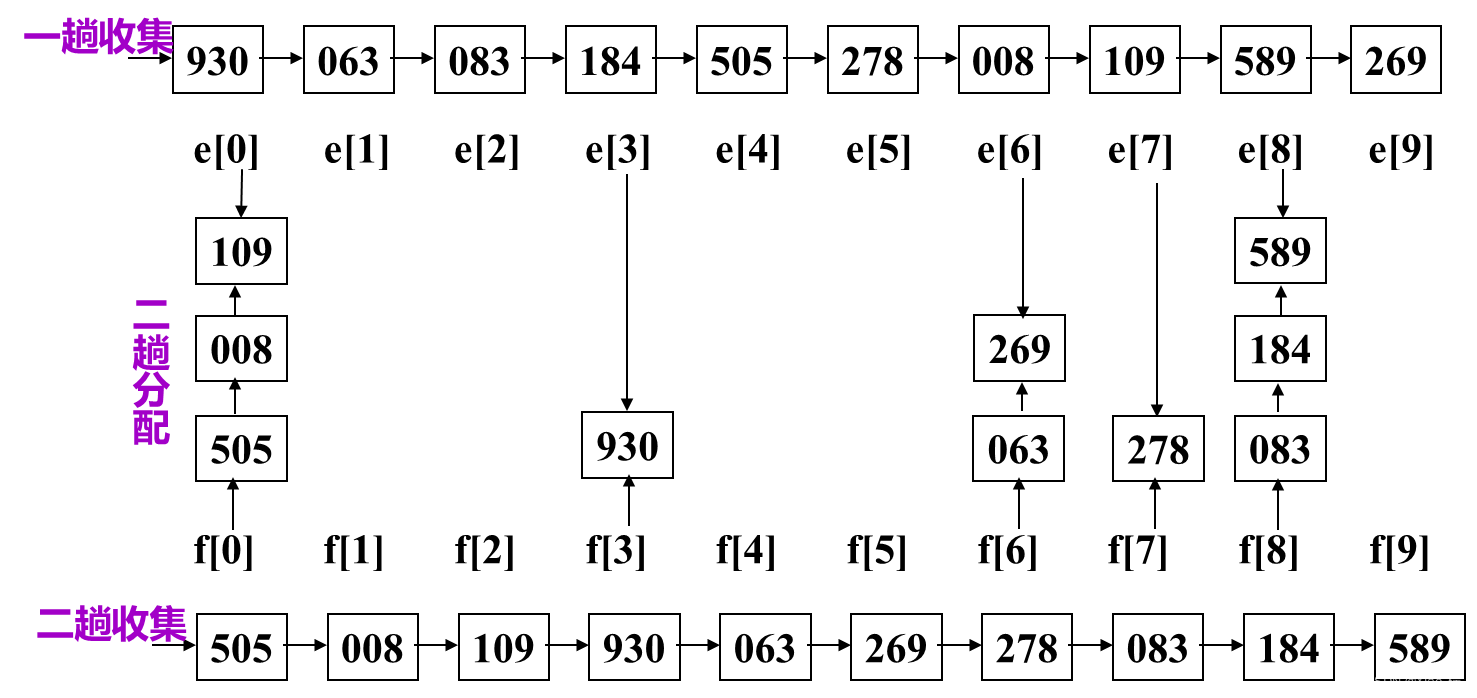
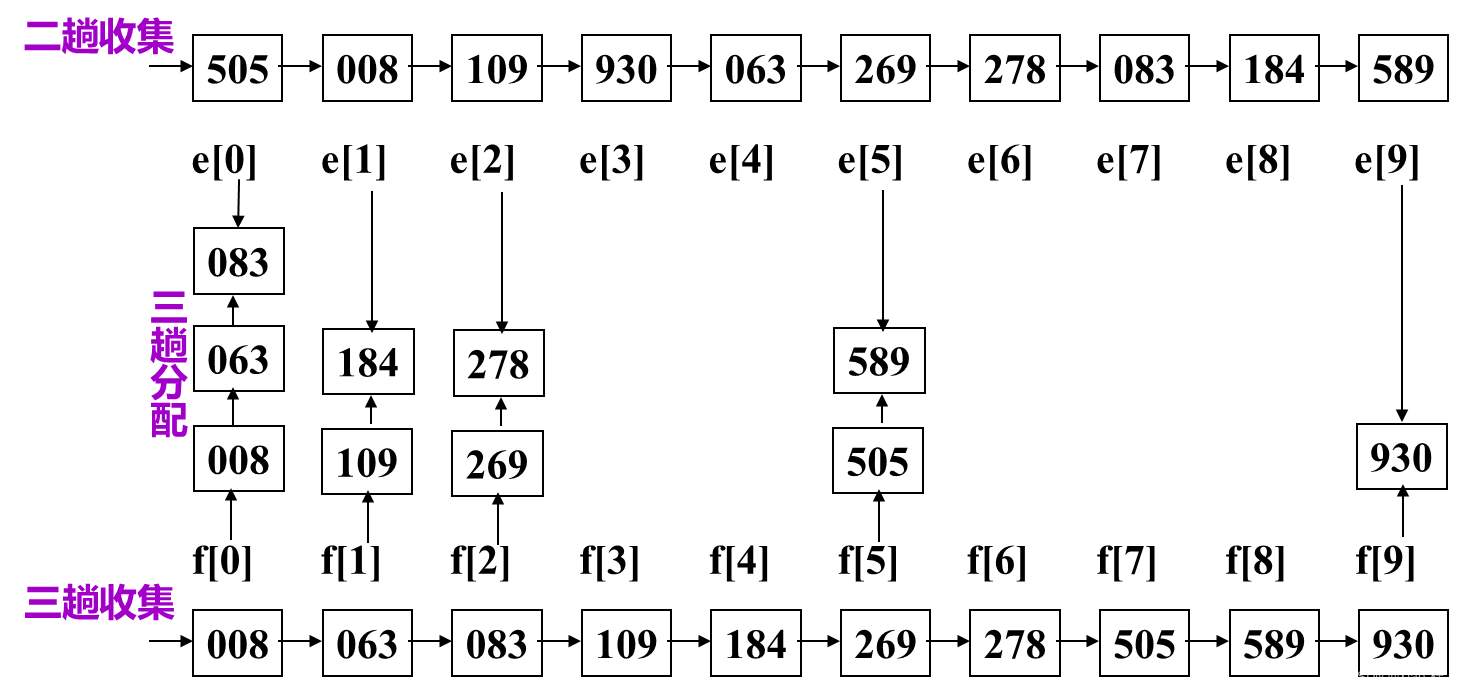
3. 链式基数排序的算法分析
若每个关键字有 d 位,关键字的基数为radix
需要重复执行d 趟“分配”与“收集”
每趟对 n 个对象进行“分配”,对radix个队列进行“收集”
时间复杂度为O(d(n+radix))
一般情况下radix表示k进制,是一个很小的值
所以时间复杂度为O(dn),其中n是记录总数,d是关键字长度d位
是一种稳定的排序方法
4. 代码实现
// 基数排序的搜索函数
int radixSearch(vector<int>& arr, int target) {// 找到数组中的最大值int maxVal = *max_element(arr.begin(), arr.end());// 对每个位数进行基数排序for (int exp = 1; maxVal / exp > 0; exp *= 10) {vector<int> count(10, 0); // 10个数字的计数数组// 统计每个数字的出现次数for (int i = 0; i < arr.size(); i++) {count[(arr[i] / exp) % 10]++;}// 计算累计出现次数for (int i = 1; i < 10; i++) {count[i] += count[i - 1];}// 构建排序后的数组std::vector<int> sortedArr(arr.size());for (int i = arr.size() - 1; i >= 0; i--) {sortedArr[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}// 更新原始数组arr = sortedArr;}// 在排序后的数组中进行二分查找int left = 0;int right = arr.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == target) {return mid;} else if (arr[mid] < target) {left = mid + 1;} else {right = mid - 1;}}// 如果未找到目标值,返回-1return -1;
}
内部排序算法比较
 快速排序、堆排序、归并排序三者比较, 简单排序包含除希尔排序外的其他时间复杂度O(n2)的多种排序,简单排序都是稳定的,在初始基本有序或n较小时,优先选择直接插入排序,它可以和快排、归并结合使用
快速排序、堆排序、归并排序三者比较, 简单排序包含除希尔排序外的其他时间复杂度O(n2)的多种排序,简单排序都是稳定的,在初始基本有序或n较小时,优先选择直接插入排序,它可以和快排、归并结合使用
基数排序适用于多关键字排序,在n很大且d较小的情况,使用链式基数排序较好
从稳定性来看,归并排序+简单排序+基数排序都是稳定的,根据实际需要选择
总结
1. 排序:内部排序(在内存中进行)、外部排序(需要使用外存)
算法复杂度包括比较次数KCN和移动次数RMN,稳定性的概念
2. 排序分类:插入排序、交换排序、选择排序、归并排序、基数排序
3. 插入排序:假定前i-1个对象有序,第i个数据找出合适位置插入
直接插入排序,时间复杂度为O(n2),是稳定排序
希尔排序,时间复杂度为O(n x(log2 n)2),是不稳定的排序方法
4. 交换排序:两个位置元素不符合排序规则,就交换两个元素
起泡排序,时间复杂度为O(n2),是一种稳定排序方法。起泡排序可以提前结束。
快速排序,时间复杂度为O(nlog2n),是一种不稳定排序方法
5. 选择排序,每一趟选出第i小(大)的元素,与第i个位置的元素交换
简单选择排序,时间复杂度为O(n2),是一种不稳定排序方法
堆排序,时间复杂度为O(nlog2n),是一种不稳定排序方法
要掌握堆判断
6. 归并排序,将两个或两个以上的有序表合并成一个新的有序表。
两路归并排序,时间复杂度为O(nlog2n),是不稳定排序,空间复杂度O(n)
7. 基数排序,多关键字排序,最低位优先法LSD
链式基数排序,时间复杂度为O(dn),是稳定排序
相关文章:

数据结构-内部排序
简介 排序(Sorting):将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列 排序算法分为内部排序和外部排序 内部排序:在排序期间数据对象全部存放在内存的排序 外部排序&am…...

Qt加载网页崩溃 ASSERT:“m_adapterClient“ in file ...
1、软件启动后加载网页无异常,点击按钮,加载新网页时崩溃 崩溃代码: QWebEngineView *createWindow(QWebEnginePage::WebWindowType type) { Q_UNUSED(type); return this; } 2、原因 Qt只是调用谷歌的浏览器引擎ÿ…...

合约短线高胜率策略-扭转乾坤指标使用说明
扭转乾坤指标使用说明 行情判断 双绿线 多趋势双红线 空趋势大绿线 小红线 多震荡大红线 小绿线 空震荡 进场条件 趋势行情进场 多趋势 多信号 底金叉 做多空趋势 空信号 顶死叉 做空 震荡行情进场 多震荡 多信号 底金叉 做多多震荡 空信号 顶死叉 做空空…...

DAY37:贪心算法738
今天写了一道题目,顺便看了一个很好的总结,这篇博客可以跳过。 Leetcode:738 单调递增的数字 因为最大的数字是9,当出现后面位数的数字比前面位数的数字小的时候,就把后面的数字都变成9,前面那个数字--。…...

计算机中的缓存与内存
在现代计算机系统中,缓存和内存扮演着至关重要的角色,它们共同协作以实现高性能和高效率的数据处理。本文将深入探讨缓存和内存的概念、功能以及它们在计算机系统中的作用。 缓存与内存:概念与功能 1. 内存(RAM)&…...

2.1总结
还是一样水更一天,就随便做了几个题,有一个周期有点长,后面更一篇长的 随手刷的一道水题,就不往今天的行程单添了 问题:最大公约数 题解:题目太水了,就是求三个数,其中两组的最大公…...
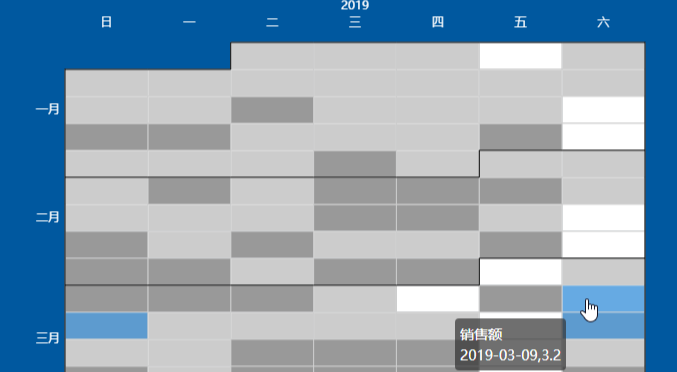
探索Pyecharts:绘制多彩日历图的艺术与技巧
Pyecharts绘制多种炫酷日历图参数说明代码实战 导言 在数据可视化领域,日历图是一种直观展示时间和数据关系的方式。Pyecharts是一个基于Echarts的Python库,可以方便地绘制各种图表,包括炫酷的日历图。本篇博客将介绍Pyecharts中绘制多种炫…...

响应标头Allow-Headers和Expose-Headers的区别和用法
Access-Control-Allow-Headers和Access-Control-Expose-Headers,简单的说,这两者都是前端和后端之间通过header传递数据的,主要的区别就是方向。 Access-Control-Allow-Headers 举个例子,如果我们前端向后端发起请求,…...

<网络安全>《13 上网行为管理》
1 概念 上网行为管理是指帮助互联网用户控制和管理对互联网的使用。其包括对网页访问过滤、上网隐私保护、网络应用控制、带宽流量管理、信息收发审计、用户行为分析等。 随着计算机、宽带技术的迅速发展,网络办公日益流行,互联网已经成为人们工作、生活…...

安全通道堵塞识别摄像机
当建筑物的安全通道发生堵塞时,可能会给人员疏散和救援带来重大隐患。为了及时识别和解决安全通道堵塞问题,专门设计了安全通道堵塞识别摄像机,它具有监测、识别和报警功能,可在第一时间发现通道堵塞情况。这种摄像机通常安装在通…...

2022 年全国职业院校技能大赛高职组云计算赛项试卷
【赛程名称】云计算赛项第二场-容器云 说明: 完成本任务需要两台安装了 CentOS7.9 操作系统的云主机: master 和 node。Chinaskill_Cloud_PaaS.iso 镜像包中有本次容器云部署所需的所有文件,运维所需的文件见附件。 某公司技术部产品开发上线…...

Android开发中,Vue 3处理回退按键事件
vue3有一些变化,按照网上有些文章的方法,发现行不通,通过一段时间的打印、尝试后,发现以下方法可行。 第一步)首先定义一个处理回退事件的js函数,一定是vue.methods中的函数,否则找不到this&am…...

three.js CSS3DRenderer、CSS3DSprite渲染HTML标签
有空的老铁关注一下我的抖音: 效果: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red;position: relative;"></div><…...

【BBF系列协议】TR369管理平台软件设计
一、介绍 旨在促进CPE和IoT的多供应商管理平台的发展。遵循TR-369协议的任何设备都可以进行管理。主要目标是促进并统一设备管理,为最终用户和服务提供商带来无数好处,减少当前技术所需的要求:设备互连、数据收集、速度、可用性等等。 二、 TR-069 ---> TR-369 物联网…...
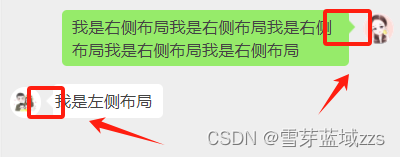
微信小程序 仿微信聊天界面
1. 需求效果图 2. 方案 为实现这样的效果,首先要解决两个问题: 2.1.点击输入框弹出软键盘后,将已有的少许聊天内容弹出,导致看不到的问题 点击输入框弹出软键盘后,将已有的少许聊天内容弹出,导致看不到的问…...

中国社会科学院大学-新加坡社科大学 招生简章
Singapore University of Social Sciences--University of Chinese Academy of Social Sciences Doctor of Business Administration (DBA) Programme in Global Strategy and Leadership 一、项目简介 全球经济正在经历由科技进步和创新、政治和人口剧烈变化所带来的巨大的不…...
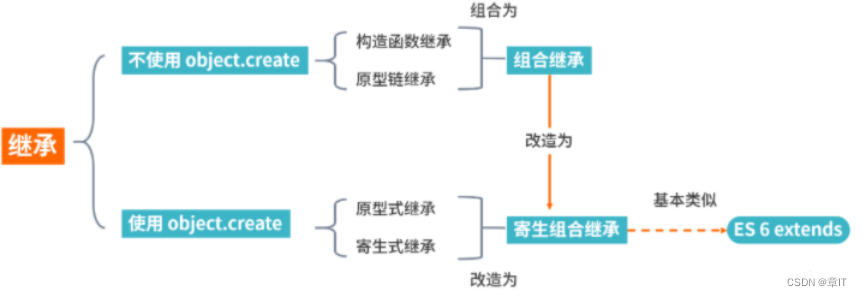
js中继承的详解(一文读懂)
文章目录 一、是什么二、实现方式原型链继承构造函数继承组合继承原型式继承寄生式继承寄生组合式继承 三、总结参考文献 一、是什么 继承(inheritance)是面向对象软件技术当中的一个概念。 如果一个类别B“继承自”另一个类别A,就把这个B称…...

Android studio使用svg矢量图
https://www.iconfont.cn/ https://www.jyshare.com/more/svgeditor/ https://editor.method.ac/ https://inloop.github.io/svg2android/ Pattern Monster - SVG 图案生成器 Android studio使用svg矢量图自适应不同的分辨率, svg矢量图绘制以及转换为And…...

《Access Path Selectionin a Relational Database Management System》论文笔记
以下是根据论文归纳出的一些查询优化器公式和知识点,有没有用不知道,先码起来。 SQL执行优化过程 处理SQL语句是从解析用户输入的SQL语句开始,经过一系列优化过程,最终生成机器代码并执行的过程。这个过程涉及到多个复杂的步骤&…...

【AI_Design】Midjourney学习笔记
目录 后缀解析Promot合格使用prompt关键词描述 关键词化合作用关键词网站推荐 联合Chatgpt使用总结 后缀解析 –ar:宽高比设置–c:多样性设置(数值0-100,默认值0)–s:风格化设置(数值0-1000&am…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
