详解 Prim 算法的实现
一、算法思路
Prim 算法是用来求最小生成树的,它的思想也有点类似于贪心——逐个将离当前集合最近的点加入到集合中,直至发现图不连通或所有点都被加到集合中,算法即宣告终止。它的具体做法是:
-
step 1:初始时,由当前最小生成树中的点构成的集合 S S S 为空,图中剩余的点到集合的距离皆为 + ∞ +\infty +∞,这一步可以用代码实现如下:
// 假定图中共有N个点 bool st[N]; // 用bool数组st来模拟集合S,若一个点i被加入集合,// 则将st[i]置为true int dist[N]; // 用dist数组来记录所有点到当前集合的最短距离, memset(dist, 0x3f, sizeof dist); // 初始时,将所有点到集合的最短// 距离置为正无穷 -
step 2:接下来是 n 轮循环,每轮循环的任务是找到当前离集合最近的点并将其加入集合(即合并到当前的最小生成树上),同时,用这个点更新其他点到集合的距离(当这个点加入集合后,其他点到集合的最短距离有可能发生改变,因为此时这个新加入的点也是集合的一部分了,所以要用这个点到其他点的距离来更新其他点到集合的最短距离),这一步的代码可以实现如下:
// n是图中所有点的个数 for (int i = 0; i < n; i++) // n轮循环,每轮循环负责将一个点加入集合中 {// 首先要找到我们要加入的点是谁int t = -1; // 先用-1来暂时表示这个点,并用t来记录// 执行具体的寻找过程:从1~n这n个点中将当前这一轮的t找出来for (int j = 1; j <= n; j++) // 从1到n循环n个点,看哪个点符合要求if (!st[t] && (t == -1 || dist[j] < dist[t])) // 如果这个点尚未在集合中,并且// 要么找到了第一个不在集合中的点,// 要么找到了离集合最短距离更小的点t = j; // 就更新t的取值// 当我们找到t以后,我们需要将t加入到集合中,st[t] = true;// 并用t到其他点的距离更新其他点到集合的最短距离for (int j = 1; j <= n; j++)dist[j] = min(dist[j], g[t][j]); } -
step 3:如何返回最终的结果呢?我们要找的是我们要返回的是最小生成树的树边权重之和(以下简记为“最小生成树的长度”),而这个长度是由一条条边加起来得到的。注意到,每次往集合中新加入一个点,就相当于当前最小生成树又多了一条边,而这条边就是我们要找的众多边之一。因此,只需要在每次新加入一条边的时候,把新加入的边的长度累加到最终的结果中去即可(这个长度即为新加入的点到集合的最短距离,即为
dist[t])。
然而如果图中根本就不存在最小生成树怎么办呢?如果在中途就发现了图中必然不可能存在最小生成树,那能不能提前停止并返回结果呢?如果可以,当如何实现呢?
答案是我们可以在加入每个点之前先做一个判断:如果新加入的点到集合的最短距离是 + ∞ +\infty +∞ ,这就意味着新加入的点跟集合中的点根本就不连通,此时图中必不可能存在最小生成树,而一旦我们发现了这样一种情况,就可以提前退出循环,并将当前结果报告出去,其实现代码如下:// 用res来记录最终最小生成树的长度 int res = 0; // 初始时res为0 for (int i = 0; i < n; i++) // 最外层的n轮循环,每轮找到一个点并加入当前集合中 {int t = -1;for (int j = 1; j <= n; j++)if (!st[j] && (t == -1 || dist[j] < dist[t]))t = j;// 找到t以后,这个t不一定是与当前集合连通的,所以可以提前做一个判断:if (i && dist[t] == INF) return INF; // 如果当前点到集合的最短距离为正无穷,则返回正无穷(最终可根据返回结果是否为正无穷来判断图中是否存在最小生成树)// 如果上一步没有提前返回,则说明当前点与集合是连通的,那么它与集合之间将会连起一条新的边,这个边是最终最小生成树的一部分,要将它累加至最后的结果中:if (i) res += dist[t];// 注意以上两步中都有一个if(i),这个判断的目的是:i=0表示第一轮循环(即将第一个点加入最小生成树),由于第一个点到初始空集合S的距离为正无穷,所以这个点不能作为“不存在最小生成树”的判断,这个点到集合的距离也不能累加至最终的结果中,因此正确的做法是跳过这个点,即加一个if(i)的判断...// 最终返回res即可return res; }
二、Prim 算法求最小生成树的完整代码如下:
#include <iostream>
#include <cstring>using namespace std;const int N = 510, M = 2e5 + 10; // 边数设为初始值的两倍,是因为无向图要加两条有向边
const int INF = 0x3f3f3f3f;int n, m;
int g[N][N];
int dist[N];
bool st[N];int prim()
{memset(dist, 0x3f, sizeof dist); // 初始时,设置所有点到集合的最短距离都为正无穷int res = 0; // 用res记录最终最小生成树的长度for (int i = 0; i < n; i++) // 然后开始n轮循环,每轮将一个点加入当前集合中{int t = -1; // 将当轮要加入的点初始化为-1for (int j = 1; j <= n; j++) // 然后从1~n这n个点中找到当前这一轮要加入的点if (!st[j] && (t == -1 || dist[j] < dist[t]))t = j;// 找到以后,先做判断,看图会不会不连通if (i && dist[t] == INF) return INF;// 如果确认当前这一轮还未发现图是不是不连通的,就先将当前边累加至最终结果if (i) res += dist[t];// 关键一步:用t到它所有邻居的距离更新它的所有邻居到当前集合的最短距离for (int j = 1; j <= n; j++) // 遍历并找到t的所有邻居dist[j] = min(dist[j], g[t][j]); // 更新邻居到当前集合的距离// 最后,将当前这个点t加入到当前集合中st[t] = true;}return res; // 返回图中最小生成树的长度
}int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g); // 初始时,设置所有边权都为正无穷// 这一步是不可省略的,因为有些点之间根本就没有连接,其距离为正无穷,// 如果不进行这一步设置,这些不连通的点之间的边将被默认初始化为0,// 这显然是不对的while (m--){int a, b, w;scanf("%d%d%d", &a, &b, &w);g[a][b] = g[b][a] = min(g[a][b], w);}int res = prim();if (res == INF) puts("impossible");else cout << res << endl;return 0;
}
【注】以上内容参考AcWing。
相关文章:

详解 Prim 算法的实现
一、算法思路 Prim 算法是用来求最小生成树的,它的思想也有点类似于贪心——逐个将离当前集合最近的点加入到集合中,直至发现图不连通或所有点都被加到集合中,算法即宣告终止。它的具体做法是: step 1:初始时…...

Android 使用高德地图
一、获取高德平台key 【1】基于application包名&sha1值在高德控制台获取key值,详情参考: 获取Key-创建工程-开发指南-Android 地图SDK | 高德地图API 【2】在manifest中声明权限 【3】将拿到的key值在manifest中进行声明 <!--允许程序打开网络…...
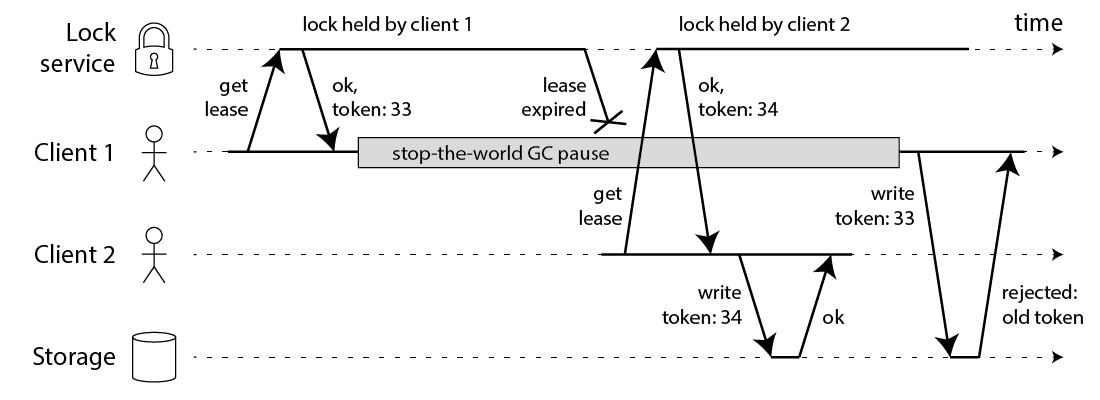
从redis setnx 来看看分布式锁
什么是分布式锁 分布式锁(多服务共享锁)在分布式的部署环境下,通过锁机制来让多客户端互斥的对共享资源进行访问/操作。 为什么需要分布式锁 在单体应用服务里,不同的客户端操作同一个资源,我们可以通过操作系统提供…...
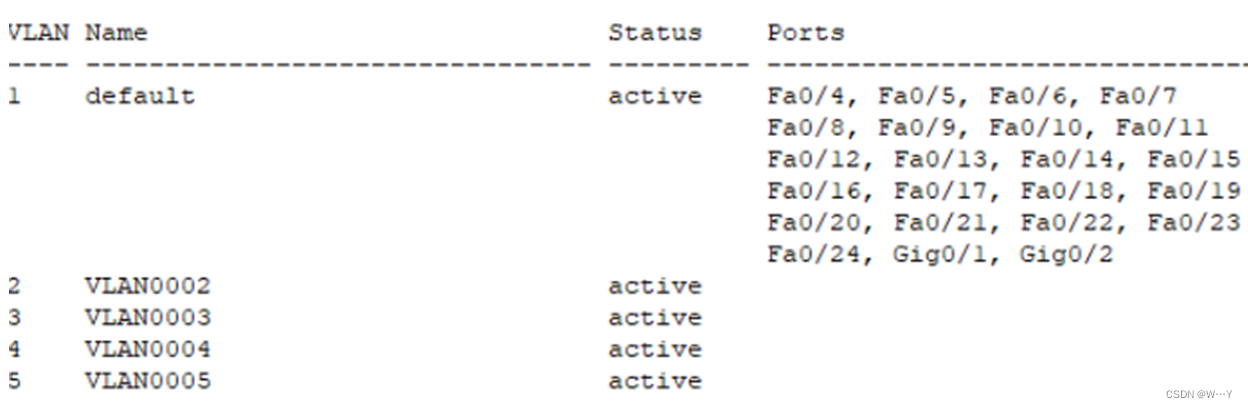
校园网网络规划与设计——计算机网络实践报告
W...Y的主页 😊 代码仓库分享💕 目录 一、设计目的 二、软硬件环境 三、理论基础 四、设计方案 五、网络配置步骤 六、设计过程中出现的问题及相应解决办法 八、参考资料 一、设计目的 深入理解网络工程的三层层次设计模型; 掌握网络…...
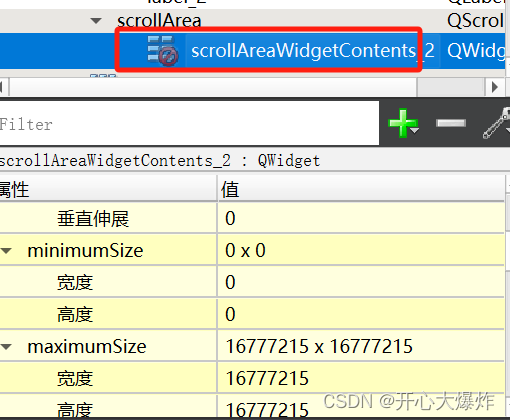
Qt QScrollArea 不显示滚动条 不滚动
使用QScrollArea时,发现添加的控件超出QScrollArea 并没有显示,且没有滚动条效果 原因是 scrollArea指的是scrollArea控件本身的大小,肉眼能看到的外形尺寸。 scrollAreaWidgetContents指的是scrollArea控件内部的显示区域,里面可…...

【SVN在Linux下的常用指令】
windows下的TortoiseSVN是资源管理器的一个插件,以覆盖图标表示文件状态,几乎所以命令都有图形界面支持,比较好用,这里就不多说。主要说说linux下svn的使用,因为linux下大部分的操作都是通过命令行来进行,所…...

2024 高级前端面试题之 Node 「精选篇」
该内容主要整理关于 Node 模块的相关面试题,其他内容面试题请移步至 「最新最全的前端面试题集锦」 查看。 Node模块精选篇 1. package.json版本号规则2. package.json 与 package-lock.json 的关3. npm 模块安装机制4. 模块化的差异 AMD CMD COMMONJS ESMODUL5. No…...
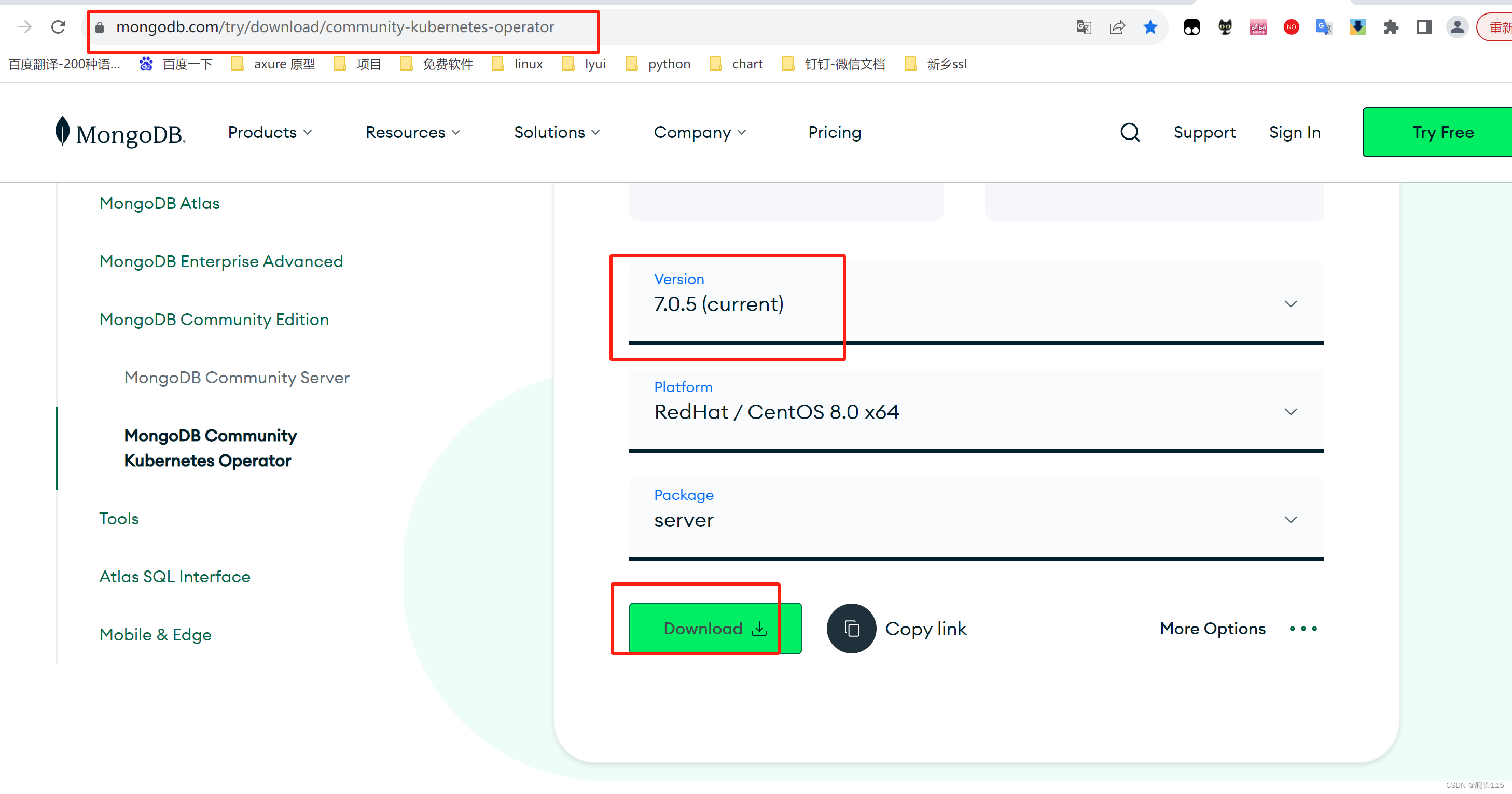
linux麒麟系统安装mongodb7.0
1.mogedb下载 下载的是他tar包 https://fastdl.mongodb.org/linux/mongodb-linux-x86_64-rhel80-7.0.5.tgz wget -o https://fastdl.mongodb.org/linux/mongodb-linux-x86_64-rhel80-7.0.5.tgz 也可以下载rpm包 2.将包上传至服务器并解压 #进入目录 并解压 cd /opt/ tar…...

Spring声明式事务
1.概念 事务就是用户定义的一系列执行SQL语句的操作, 这些操作要么完全地执行,要么完全地都不执行, 它是一个不可分割的工作执行单元 一个使用Mybatis-Spring的主要原因是它允许Mybatis参与到Spring的事务管理中,而不是给Mybatis创建一个新的…...

PyTorch深度学习实战(34)——Pix2Pix详解与实现
PyTorch深度学习实战(34)——Pix2Pix详解与实现 0. 前言1. 模型与数据集1.1 Pix2Pix 基本原理1.2 数据集分析1.3 模型构建策略 2. 实现 Pix2Pix 生成图像小结系列链接 0. 前言 Pix2Pix 是基于生成对抗网络 (Convolutional Generative Adversarial Netwo…...
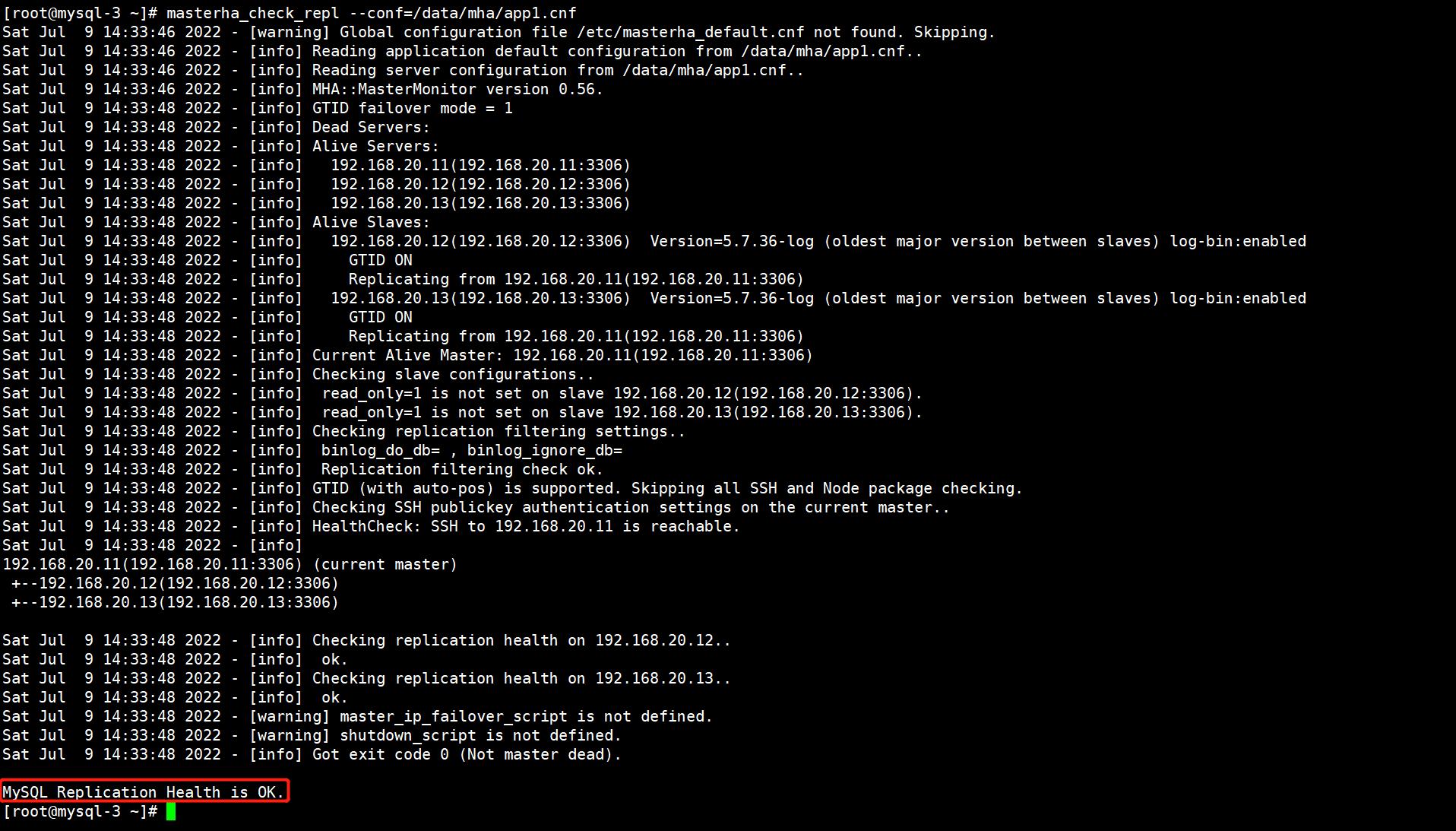
第96讲:MySQL高可用集群MHA的核心概念以及集群搭建
文章目录 1.MHA高可用数据库集群的核心概念1.1.主从复制架构的演变1.2.MHA简介以及架构1.3.MHA的软件结构1.4.MHA Manager组件的启动过程1.5.MHA高可用集群的原理 2.搭建MHA高可用数据库集群2.1.环境架构简介2.2.搭建基于GTID的主从复制集群2.2.1.在三台服务器中分别搭建MySQL实…...

外星人入侵(python)
前言 代码来源《python编程从入门到实践》Eric Matthes 署 袁国忠 译 使用软件:PyCharm Community Editor 2022 目的:记录一下按照书上敲的代码 alien_invasion.py 游戏的一些初始化设置,调用已经封装好的函数方法,一个函数的…...
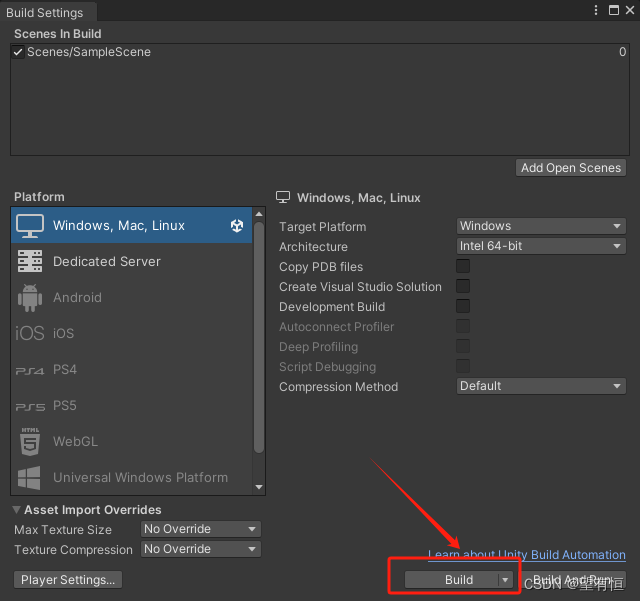
Unity中开发程序打包发布
添加ESC脚本 使用Unity打包发布的过程中,考虑到打开的程序会处于全屏界面,而此时我们又会有退出全屏的需求,因此需要添加ESC脚本,当我们单击ESC脚本的过程中,退出全屏模式。 在Assets/Scenes下,创建esc.cs…...
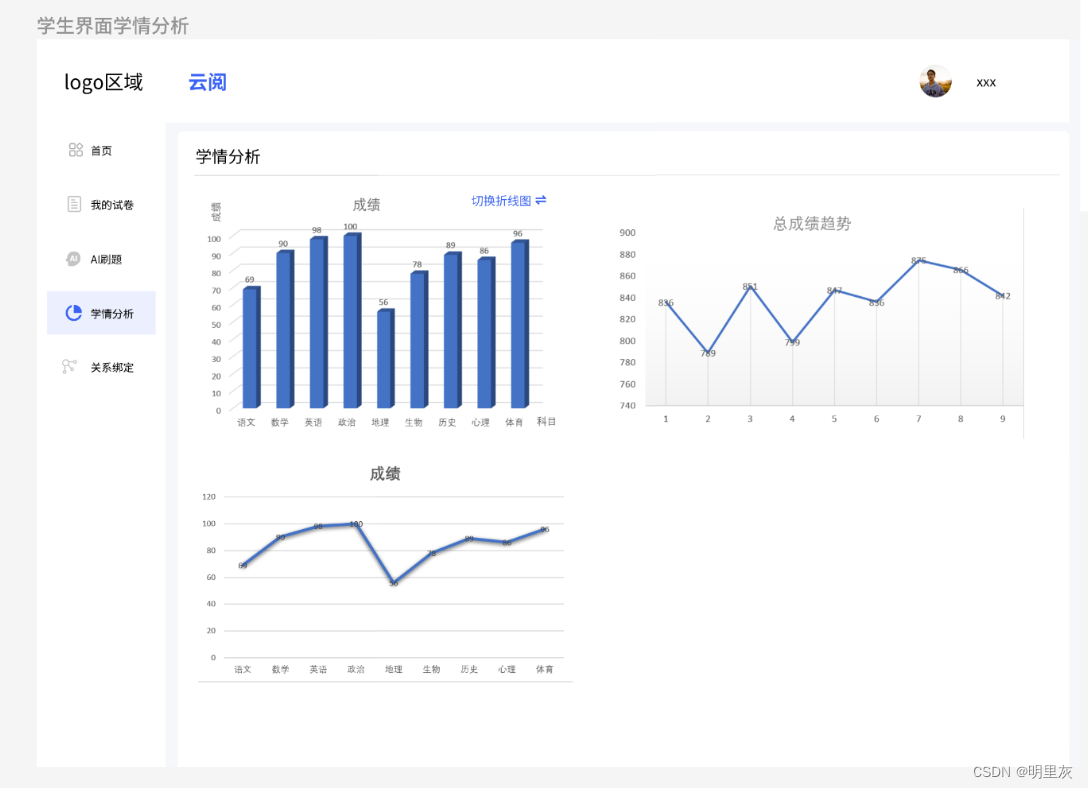
2024.2.1日总结
web的运行原理: 用户通过浏览器发送HTTP请求到服务器(网页操作)。web服务器接收到用户特定的HTTP请求,由web服务器请求信息移交给在web服务器中部署的javaweb应用程序(Java程序)。启动javaweb应用程序执行…...

LeetCode解法汇总2670. 找出不同元素数目差数组
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 描述: 给你一个下…...
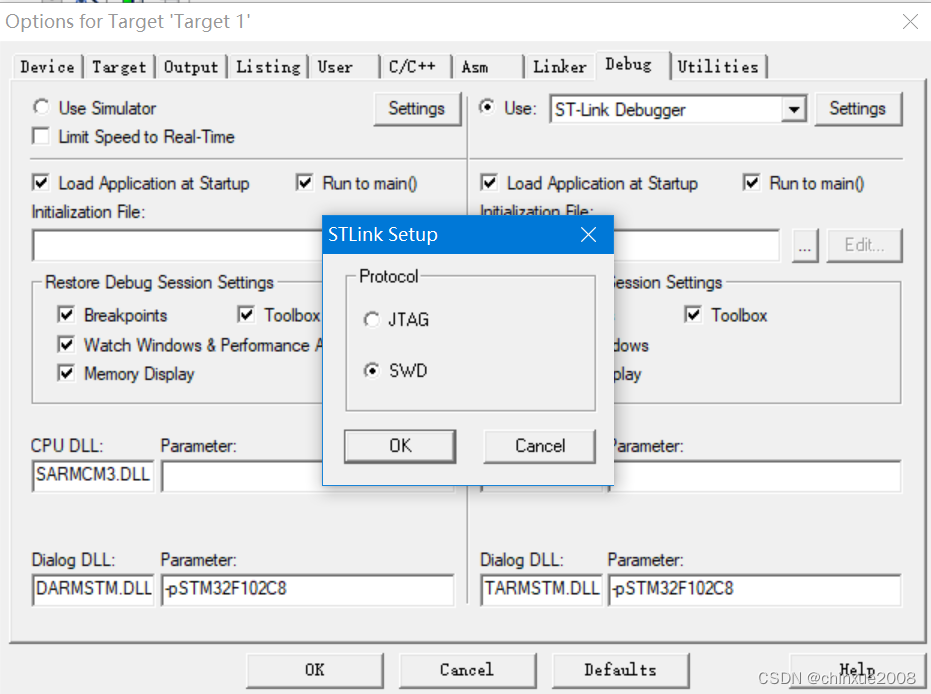
STM32目录结构
之前一直头疼的32目录,比51复杂,又没有C规律,也不像python脚本文件关联不强,也不像工整的FPGA工程,编的时候到处放,爆出的错千奇百怪。短暂整理了一个,还是没有理得很轻。 startup_stm32f10x_m…...

算法专题:记忆搜索
参考练习习题总集 文章目录 前置知识练习习题87. 扰乱字符串97. 交错字符串375. 猜数字大小II403. 青蛙过河464. 我能赢吗494. 目标和552. 学生出勤记录II576. 出借的路径数 前置知识 没有什么特别知识,只有一些做题经验。要做这类型的题目,首先写出暴…...

【数据分享】1929-2023年全球站点的逐日最低气温数据(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标,其中又以气温指标最为常用!说到气温数据,最详细的气温数据是具体到气象监测站点的气温数据! 之前我们分享过1929-2023年全球气象站…...
)
2024美赛数学建模D题思路+模型+代码+论文(持续更新)
2024美赛数学建模A题B题C题D题E题F题思路模型代码论文:开赛后第一时间更新,获取见文末名片 组队环节: 美赛最多是3个人参赛,一般的队伍都是由三人组成(当然如果你很大佬也可以一个人参赛),队伍…...
dubbo+sentinel最简集成实例
说明 在集成seata后,下面来集成sentinel进行服务链路追踪管理~ 背景 sample-front网关服务已配置好 集成 一、启动sentinel.jar 1、官网下载 选择1:在本地启动 nohup java -Dserver.port8082 -Dcsp.sentinel.dashboard.serverlocalhost:8082 -Dp…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
