洛谷P8599 [蓝桥杯 2013 省 B] 带分数
[蓝桥杯 2013 省 B] 带分数
题目描述
100 100 100 可以表示为带分数的形式: 100 = 3 + 69258 714 100 = 3 + \frac{69258}{714} 100=3+71469258。
还可以表示为: 100 = 82 + 3546 197 100 = 82 + \frac{3546}{197} 100=82+1973546。
注意特征:带分数中,数字 1 1 1 ~ 9 9 9 分别出现且只出现一次(不包含 0 0 0)。
类似这样的带分数, 100 100 100 有 11 11 11 种表示法。
输入格式
从标准输入读入一个正整数 N ( N < 1 0 6 ) N(N<10^6) N(N<106)。
输出格式
程序输出数字 N N N 用数码 1 1 1 ~ 9 9 9 不重复不遗漏地组成带分数表示的全部种数。
注意:不要求输出每个表示,只统计有多少表示法!
样例 #1
样例输入 #1
100
样例输出 #1
11
样例 #2
样例输入 #2
105
样例输出 #2
6
提示
原题时限 3 秒, 64M。蓝桥杯 2013 年第四届省赛
暴力做法
要保证1~9这每个数都要出现,且仅出现一次,可以联想到AcWing 842. 排列数字该暴力解法,就是在排列数字的基础上,将9个数的自由排列先求出来,然后根据式子
n = a + b c n = a + \frac{b}{c} n=a+cb
的基础上,枚举每一个a, b的位数,双重循环,c的位数可以由9 - a - b求出,通过get_value函数将每个求出来,再验证式子是否正确,由于c++中的除法是取整后的结果,所以要转换成乘法在进行验证。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <math.h>
using namespace std;const int N = 15;int path[N];//九个数的自由排列结果
bool st[N];
int n, res = 0;int get_value(int k, int c){// k为起始下标,c为总位数int res = 0;for (int i = 0; i < c; i ++){res += path[k + i] * pow(10, c - i - 1);}return res;
}void dfs(int k){if (k == 9){for (int i = 1; i < 9; i ++){int a = get_value(0, i);if (a > n) break;//a如果大于n就一定等式不成立,提前剪枝for (int j = 1; j < 9 - i; j ++){int k = 9 - i - j;if (k <= 0) break;else{int b = get_value(i, j);int c = get_value(i + j, k);if (n * c == a * c + b ){//这里必须要变形成乘法形式,因为除法是取整除法会导致答案过多res ++;}}}}return;}for (int i = 1; i <= 9; i ++){if (!st[i]){st[i] = true;path[k] = i;dfs(k + 1);st[i] = false;}}
}int main(){scanf("%d", &n);dfs(0);printf("%d", res);return 0;
}

要开 O 2 O_2 O2优化,不然超过1s了TLE
嵌套dfs
首先通过传入参数的形式将a, c的值求出来,减少了多次求的运算过程,通过先dfs_a, 中嵌套dfs_c,枚举所有结果,用check进行剪枝,来加快处理速度。
b = n( 1 0 6 10^6 106) * c(10^6) 爆int( 1 0 10 10^{10} 1010)了,所以要用 l o n g l o n g long long longlong来存b
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 20;
typedef long long LL;bool st[N], backup[N];
int n, res = 0;bool check(int a, int c){//判断当前a, c是否满足题目的要求LL b = n * (LL)c - a * c;if (!a || !b || !c) return false; //当a, b, c为零时不满足,边界特判memcpy(backup, st, sizeof st);//由于b中的数字可能重复,所以需要改变st中的值判断重复,但这影响了st,所以要先复制while (b){//将b中的每个数字都抠出来int x = b % 10;b /= 10;if (!x || backup[x]) return false; backup[x] = true;}for (int i = 1; i <= 9; i ++){if (!backup[i]) return false;}return true;
}void dfs_c(int k, int a, int c){if(k == n) return;if (check(a, c)) res ++;//当前c不满足,也要接着后面代码找下一个c,不能returnfor (int i = 1; i <= 9; i ++){if (!st[i]){st[i] = true;dfs_c(k + 1, a, c * 10 + i);st[i] = false;}}
}void dfs_a(int k, int a){if (a > n) return;dfs_c(k, a, 0);for (int i = 1; i <= 9; i ++){if (!st[i]){st[i] = true;dfs_a(k + 1, a * 10 + i);st[i] = false;}}
}int main(){scanf("%d", &n);dfs_a(0, 0);//枚举到第几位,a的值为多少printf("%d\n", res);return 0;
}
相关文章:

洛谷P8599 [蓝桥杯 2013 省 B] 带分数
[蓝桥杯 2013 省 B] 带分数 题目描述 100 100 100 可以表示为带分数的形式: 100 3 69258 714 100 3 \frac{69258}{714} 100371469258。 还可以表示为: 100 82 3546 197 100 82 \frac{3546}{197} 100821973546。 注意特征:带分…...

grafana安装DevOpsProdigy KubeGraf 1.5.2
安装DevOpsProdigy KubeGraf需要安装kube-state-metrics 官方地址:https://github.com/kubernetes/kube-state-metrics/tree/release-2.10/examples/standard 查看k8s版本和kube-state-metrics对应版本: [rootmaster1 kube-state-metrics]# ll 总用量 …...
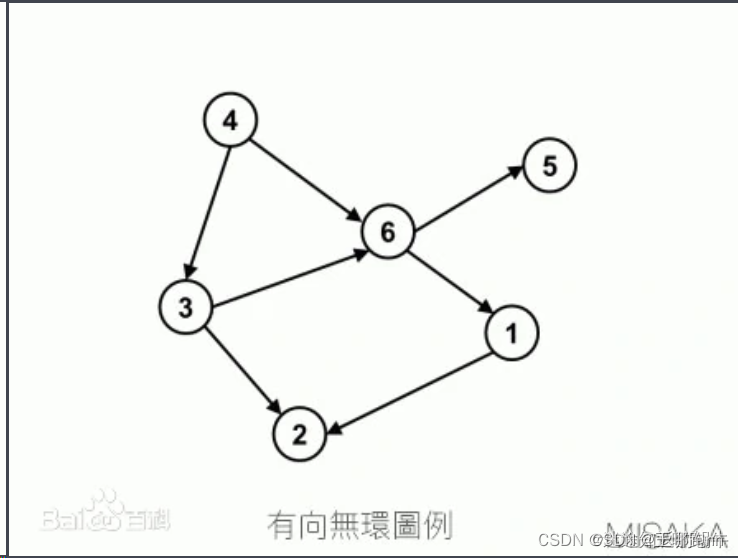
大数据 - Hadoop系列《三》- MapReduce(分布式计算引擎)概述
上一篇文章: 大数据 - Hadoop系列《三》- HDFS(分布式文件系统)概述-CSDN博客 目录 12.1 针对MapReduce的设计构思 1. 如何对付大数据处理场景 2. 构建抽象编程模型 3. 统一架构、隐藏底层细节 12.2 分布式计算概念 12.3 MapReduce定义…...
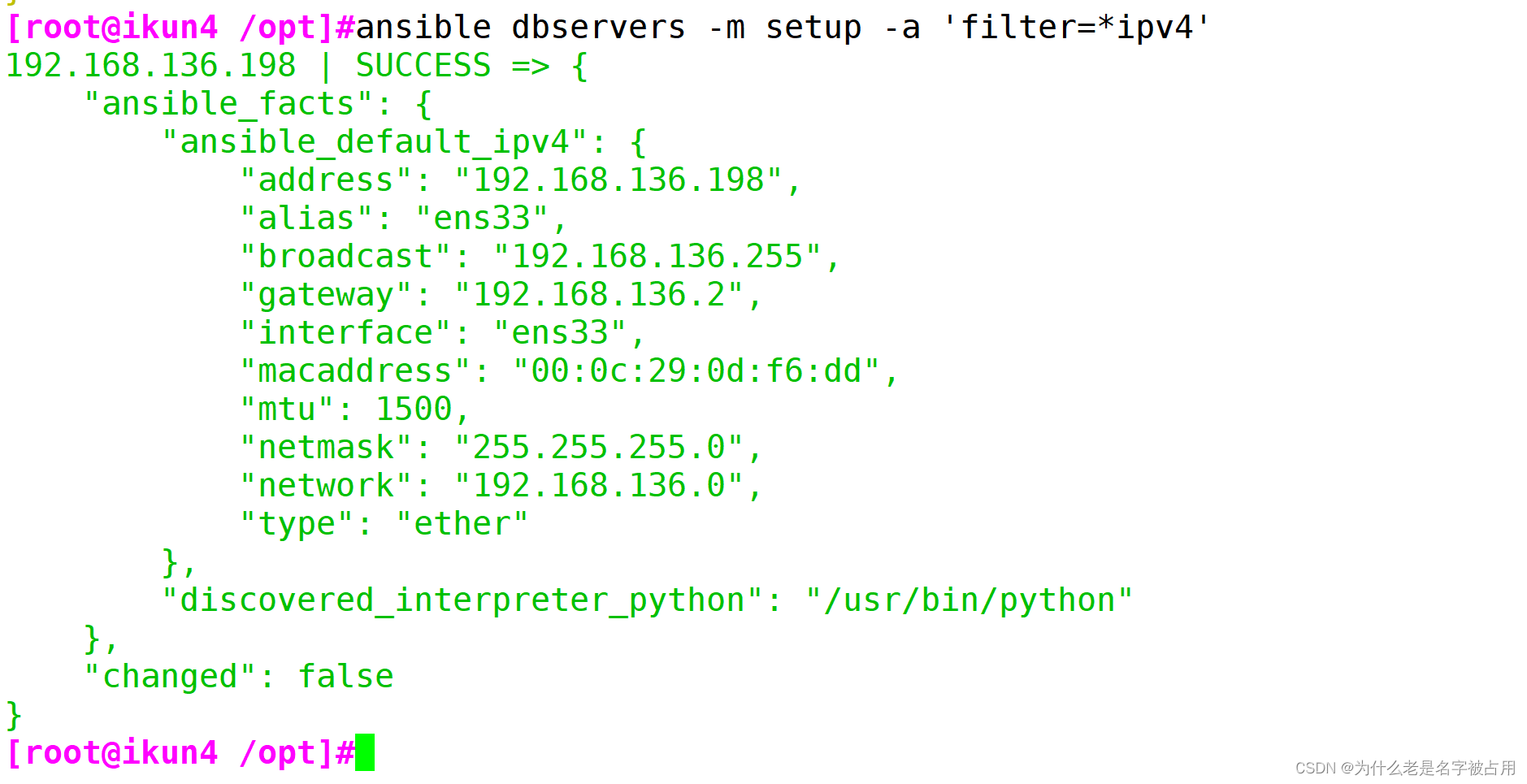
了解Ansible自动化运维工具及模块的使用
一、Ansible的相关知识 1.1 Ansible工具的了解 Ansible是一个基于Python开发的配置管理和应用部署工具,现在也在自动化管理领域大放异彩。它融合了众多老牌运维工具的优点,Pubbet和Saltstack能实现的功能,Ansible基本上都可以实现。Ansible…...
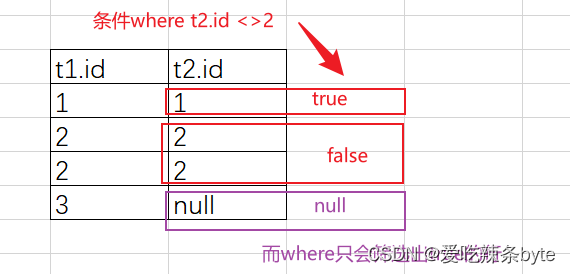
sql指南之null值用法
注明:参考文章: SQL避坑指南之NULL值知多少?_select null as-CSDN博客文章浏览阅读2.9k次,点赞7次,收藏21次。0 引言 SQL NULL(UNKNOW)是用来代表缺失值的术语,在表中的NULL值是显示…...

常见消息队列:ActiveMQ、RabbitMQ、RocketMQ、Kafka的区别总结
目录 前言 1、常见消息队列 1.ActiveMQ 2.RabbitMQ 3.RocketMQ 4.Kafka 2、区别 1.消息传递模型 2.消息持久化 3.消息顺序性 4.可靠性 5.生态系统和社区支持 6.表格对比 前言 消息队列可以实现应用程序之间的异步通信,能够实现异步消息的发送和接收&am…...

火柴人大逃亡
欢迎来到程序小院 火柴人大逃亡 玩法:左右两边火柴人,点击左边左边火柴人跳跃,点击右边右边跳跃, 上下快速移动道路,躲过障碍物,看你能坚持多久,快去火柴人大逃亡吧^^。开始游戏https://www.or…...
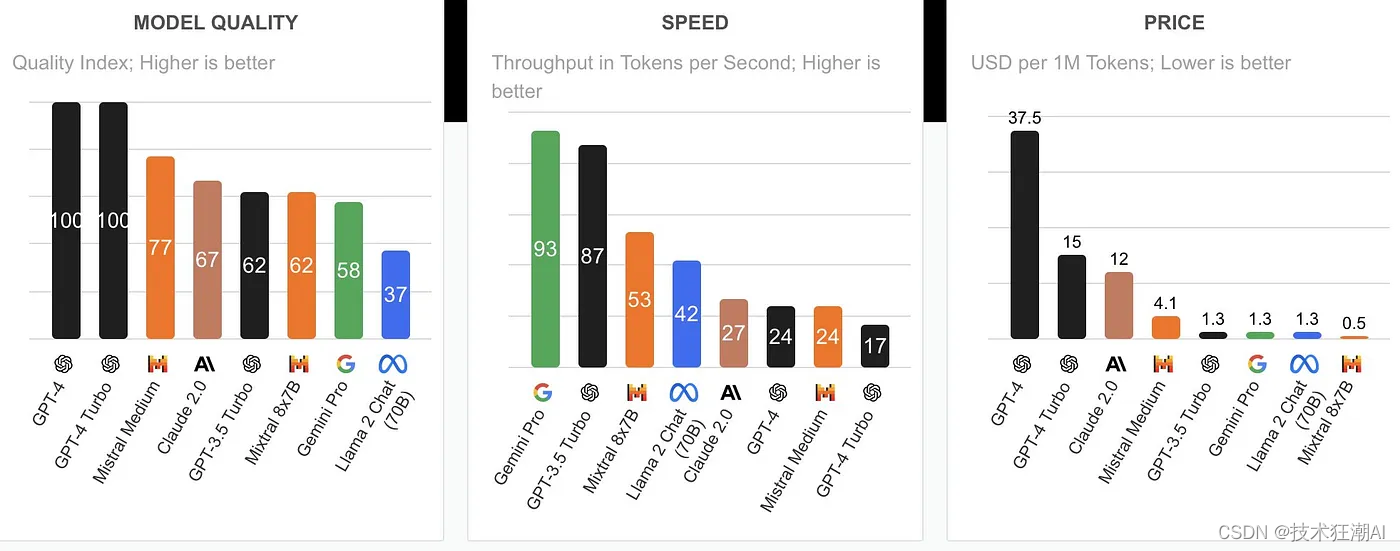
AI革命新篇章:法国天才团队挑战ChatGPT霸主地位
Mistral AI: Guillaume Lample, Arthur Mensch et Timothe Lacroix. ChatGPT 的霸主地位已被三位来自法国的天才所颠覆!如上图这三个人,其中一位曾在 DeepMind 工作,另外两位来自 Meta,他们联手为 AI 领域带来了革命性的变革 我…...

数据双向绑定v-modal
v-model v-model就实现了双向数据绑定,实际上它就是通过Vue提供的事件机制。即在子组件通过$emit()触发一个事件,在父组件使用v-on来监听对应的事件并修改相应的数据。 input的v-model就是通过<input :value"value" input"input"…...

Docker 容器jar 运行报错 at sun.awt.FontConfiguration.getVersion 解决方法
docker jar 运行报错 at sun.awt.FontConfiguration.getVersion 初步判断是在运行 Docker 容器中的 JAR 文件时遇到了与字体配置相关的问题。这个问题可能是由于容器内缺少字体配置或字体文件而引起的。 要解决这个问题,你可以尝试以下方法: 1.安装字…...

光学3D表面轮廓仪服务超精密抛光技术发展
随着技术的不断进步,精密制造领域对材料表面的处理要求越来越高,超精密抛光技术作为当下表面处理的尖端技术,对各种高精密产品的生产起到了至关重要的作用,已广泛应用于集成电路制造、医疗器械、航空航天、3C电子、汽车、精密模具…...

详解C++中auto关键字
auto关键字 auto关键字(C11)类型别名思考auto简介auto的使用细则auto与指针和引用结合起来使用在同一行定义多个变量 auto不能推导的场景1.auto不能作为函数的参数2.auto不能直接用来声明数组 auto关键字(C11) 类型别名思考 随着程序越来越复杂,程序中用到的类型也…...

24.云原生ArgoCD高级之数据加密seale sealed
云原生专栏大纲 文章目录 数据加密之seale sealedBitnami Sealed Secrets介绍Bitnami Sealed Secrets工作流程安装sealed-secrets和kubeseal安装sealed-secrets-controller安装kubeseal通过kubeseal将sealed-secrets公钥拿出来通过kubeseal加密secrets替换kustomize下secret为…...

线性代数:线性方程组
目录 一、线性方程组概念 二、消元法求线性方程组 三、系数阵的秩与线性方程组的解 无解 唯一解 无数解 相关定理 一、线性方程组概念 二、消元法求线性方程组 三、系数阵的秩与线性方程组的解 无解 唯一解 无数解 相关定理...

标准的排序组合-算法
题目 有若干个字母,要求计算出长度为4的所有可能得组合 解题 排序组合最适用的就是回溯了,建议大家本地debug一层一层的看能好理解点 private static void getResult(List<String> source, Stack<String> temp, int curLength, int maxL…...

2402C++,C++递归取各种节点名字
参考 explicit FindNamedClassVisitor(ASTContext *Context) : Context(Context) {}元<类 T>极 动作(T&e){串 ae->getQualifiedNameAsString();d.加(a);中 真;} bool VisitCXXRecordDecl(CXXRecordDecl *e) {中 动作(e);} bool VisitFunctionDecl(FunctionDecl*e…...
Qt 5.9.4 转 Qt 6.6.1 遇到的问题总结(三)
1.QSet: toList 中的toList 函数已不存在,遇到xx->toList改成直接用,如下: 2.开源QWT 图形库中QwtDial中的 setPenWidth 变成 setPenWidthF函数。 3.QDateTime 中无setTime_t 改为了setSecsSinceEpoch函数。 4.QRegExp 类已不存在 可以用Q…...
Logstash 7.7.1版本安装系统梳理
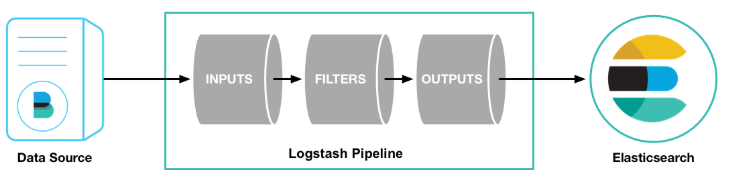
前言 上一篇文章介绍了 《ElasticSearch7.7.1集群搭建 & Kibana安装》,今天说一下 Logstash的安卓和配置; Logstash是一个开源的数据收集引擎,具有实时管道功能。它可以动态地将来自不同数据源的数据统一起来,并将数据标准化…...

4. sass实用函数归纳
4. sass实用函数归纳 字符串函数 1、quote(string) 给字符串添加引号 quote(xiaoming) // "xiaoming"2、unquote(string) 移除字符串的引号 unquote("xiaoming") // xiaoming3、str-index(string, substring) 返回 substring 子字符串第一次在 stri…...

《元梦之星》赛季更新带来“新”内容,为何却被玩家集体声讨?
前段时间,《元梦之星》迎来了“山海奇遇”赛季的重磅更新,诸多“新”内容的上线吸引了很多玩家们的关注,然而在新版本开启之后没有多,新玩法新时装甚至是游戏中的新改动都引起了不少玩家的不满。 在新赛季开启之后,玩家…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
