当前位置： 首页 > news >正文

jenkins pipeline配置maven可选参数

news 2026/2/10 7:32:16

1、在Manage Jenkins下的Global Tool Configuration下对应的maven项添加我们要用得到的不同版本的maven安装项
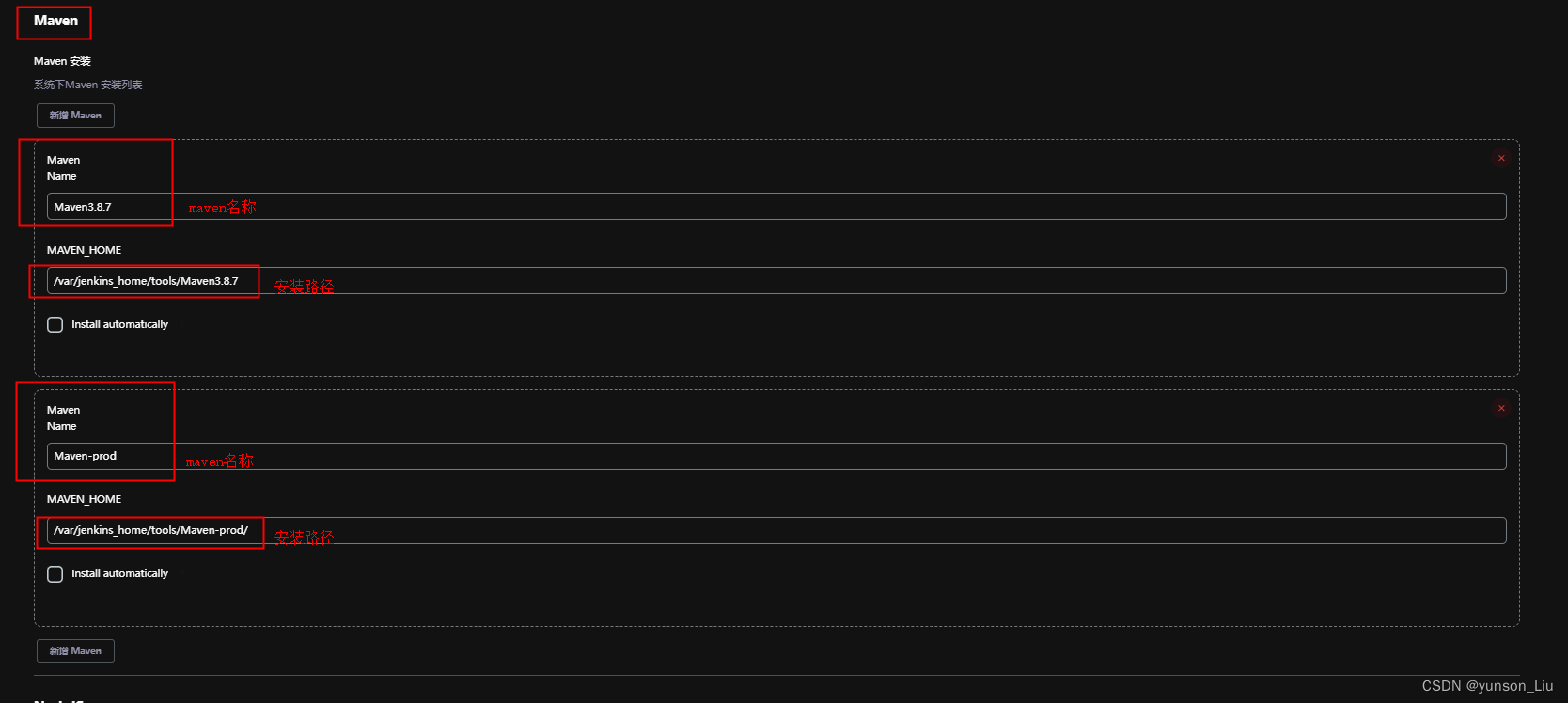
在这里插入图片描述

2、pipeline文件内容具体如下
我们maven是单一的，所以我们都是配置单选参数

pipeline {agent anyparameters {gitParameter(name: 'BRANCH_TAG', type: 'PT_BRANCH_TAG', branchFilter: 'origin/(.*)', defaultValue: 'main', selectedValue: 'DEFAULT', sortMode: 'DESCENDING_SMART', description: '请选择需要部署的代码：')choice(name: 'mode', choices: ['deploy','rollback'], description: '请选择发布或者回滚？')choice(name: 'MAVEN_VERSION', choices: ['Maven-prod', 'Maven3.8.7'], description: 'Select Maven version') }tools{jdk 'java8'//maven 'Maven-prod'maven "${MAVEN_VERSION}"}。。。。省略       
}

执行Jenkins如下
在这里插入图片描述

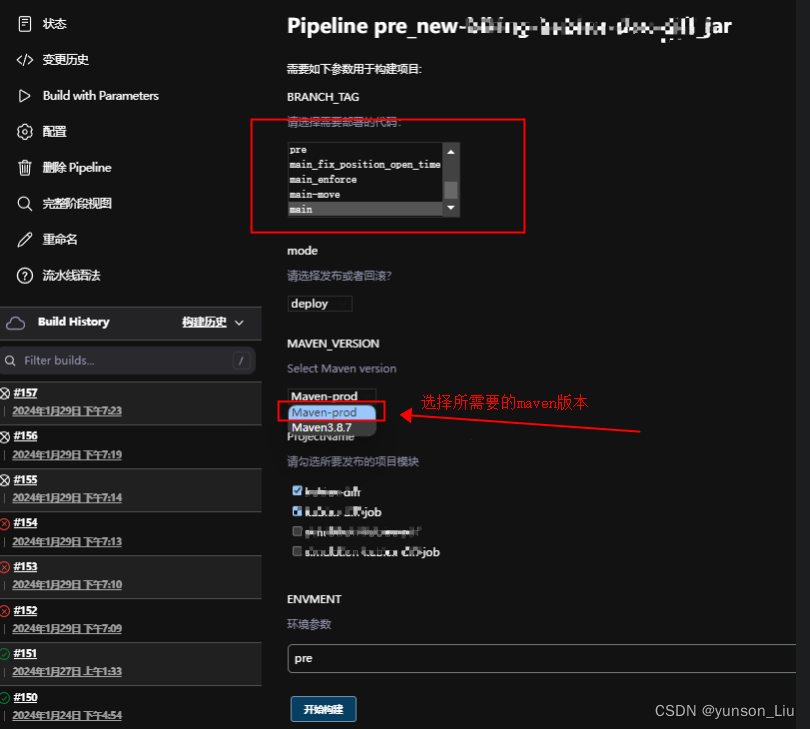
相关文章：

jenkins pipeline配置maven可选参数

1、在Manage Jenkins下的Global Tool Configuration下对应的maven项添加我们要用得到的不同版本的maven安装项 2、pipeline文件内容具体如下 我们maven是单一的，所以我们都是配置单选参数 pipeline {agent anyparameters {gitParameter(name: BRANCH_TAG, type: …...

编程日记 2024/2/3 4:31:28

【博士每天一篇论文-算法】Continual Learning Through Synaptic Intelligence，SI算法

阅读时间：2023-11-23 1 介绍 年份：2017 作者：Friedemann Zenke，巴塞尔大学弗里德里希米歇尔研究所(FMI) Ben Poole，谷歌 DeepMind 研究科学家 期刊： International conference on machine learning. PMLR…...

编程日记 2024/2/3 4:30:26

【软件工程】建模工具之开发各阶段绘图——UML2.0常用图实践技巧（功能用例图、静态类图、动态序列图状态图活动图）

更多示例图片可以参考：（除了常见的流程图，其他都有） 概念：类图 静态：用例图 动态：顺序图&状态图&活动图 1、【面向对象】UML类图、用例图、顺序图、活动图、状态图、通信图、构件图、部…...

编程日记 2024/2/3 4:28:24

Typora导出word

Typora导出word Typora是一款简洁易用的Markdown编辑器, Pandoc是一个文档转换工具，可以将Markdown格式的文档转换为其他格式，如HTML、PDF等. linux下安装 Pandoc : sudo apt install -y pandoc安装成功后,typora 会自动监测到. 然后 点击文件->…...

编程日记 2024/2/3 4:27:23

CSS 星空按钮

<template><button class="btn" type="button"><strong>星空按钮</strong><div id="container-stars"><div id="stars"></div></div><div id="glow"><div class=…...

编程日记 2024/2/3 4:25:22

Kotlin快速入门系列10

Kotlin的委托 委托模式是常见的设计模式之一。在委托模式中&#xff0c;有两个对象参与处理同一个请求&#xff0c;接受请求的对象将请求委托给另一个对象来处理。与Java一样&#xff0c;Kotlin也支持委托模式&#xff0c;通过关键字by。 类委托 类的委托即一个类中定义的方…...

编程日记 2024/2/3 4:20:17

Docker中配置MySql环境

目录 一、简单安装 1. 首先从Docker Hub中拉取镜像 2. 启动尝试创建MySQL容器&#xff0c;并设置挂载卷。 3. 查看mysql8这个容器是否启动成功 4. 如果已经成功启动&#xff0c;进入容器中简单测试 4.1 进入容器 4.2 登录mysql中 4.3 进行简单添加查找测试 二、主从复…...

编程日记 2024/2/3 4:16:14

智慧文旅：驱动文化与旅游融合发展的新动力

随着科技的快速发展和人们生活水平的提高&#xff0c;文化和旅游的融合成为了时代发展的必然趋势。智慧文旅作为这一趋势的引领者&#xff0c;通过先进的信息技术手段&#xff0c;推动文化与旅游的深度融合&#xff0c;为产业的发展注入新的活力。本文将深入探讨智慧文旅如何成…...

编程日记 2024/2/3 4:15:13

wordpress怎么做产品展示站？推荐使用MOK主题和ent主题

大多数WordPress站点都是个人博客网站&#xff0c;主要以文章性质的图文为主。不过部分站长想要用WordPress搭建一个产品展示站&#xff0c;应该怎么做呢&#xff1f; 其实&#xff0c;WordPress可以用来建立各种各样的博客网站&#xff0c;包括个人博客、企业网站、商城、影视…...

编程日记 2024/2/3 4:13:11

8、应急响应-战前溯源反制主机蜜罐系统HFishHIDSElkeidWazuh

用途&#xff1a;个人学习笔记&#xff0c;欢迎指正 目录 背景&#xff1a; 一、潮源反制-平台部署-蜜罐-Hfish 二、溯源反制-平台部署-HIDS-Wazuh 三、溯源反制-平台部署-HlDS-Elkeid-hub 背景&#xff1a; 攻击者对服务器存在着各种威胁行为&#xff0c;作为安全人员&am…...

编程日记 2024/2/3 4:12:10

LeetCode：283. 移动零

283. 移动零 1&#xff09;题目2&#xff09;代码方法一&#xff1a;两层for循环方法二&#xff1a;使用双指针 3&#xff09;结果方法一结果方法二结果 1&#xff09;题目 给定一个数组 nums&#xff0c;编写一个函数将所有 0 移动到数组的末尾&#xff0c;同时保持非零元素的…...

编程日记 2024/2/3 4:10:09

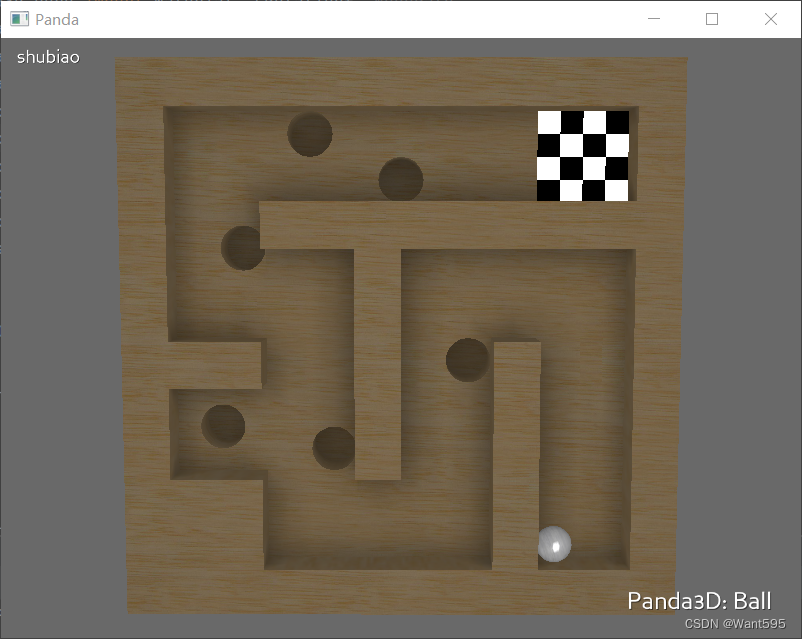
游戏开发丨基于Panda3D的迷宫小球游戏

文章目录 写在前面Panda3D程序设计程序分析运行结果系列文章写在后面 写在前面 本期内容 基于panda3d的迷宫中的小球游戏 所需环境 pythonpycharm或anacondapanda3d 下载地址 https://download.csdn.net/download/m0_68111267/88792121 Panda3D Panda3D是一种开放源代码…...

编程日记 2024/2/3 4:07:06

微信小程序 安卓/IOS兼容问题

一、背景 在开发微信小程序时&#xff0c;不同的手机型号会出现兼容问题&#xff0c;特此记录一下 二、安卓/IOS兼容问题总结 2.1、new Date()时间转换格式时&#xff0c;IOS不兼容 问题&#xff1a;在安卓中时间格式2024-1-31 10:10:10&#xff0c;但是在iOS中是不支持 &q…...

编程日记 2024/2/3 4:06:05

结构体--共用体--枚举 之难点——链表 奋力学习嵌入式的第十六天

结构体 注意&#xff1a; 1.结构体类型 可以定义在 函数里里面 但是此时作用域就被限定在该函数中 2.结构体定义形式 //形式一 限定一类型 后定义变量 struct stu { ... }; struct stu s; //形式二 定义类型的同时 定义变量 struct stu { ... }s1,s2,*s3,s4[10]; struc…...

编程日记 2024/2/3 4:05:04

猜凶手

日本某地发生了一件谋杀案&#xff0c;警察通过排查确定杀人凶手必为4个嫌疑犯的一个。 以下为4个嫌疑犯的供词: A说&#xff1a;不是我。 B说&#xff1a;是C。 C说&#xff1a;是D。 D说&#xff1a;C在胡说 已知3个人说了真话&#xff0c;1个人说的是假话。 现在请根据这…...

编程日记 2024/2/3 4:02:02

python-自动化篇-运维-实现读取日志文件最后一行的时间

文章目录 1. 使用Python打开日志文件2.python读取文件最后一行两种方式3.读取当前时间&#xff0c;进行两者相减&#xff0c;超时报警4.将内容推送到企业微信5. 关闭日志文件整体代码 1. 使用Python打开日志文件 在开始实时读取日志文件之前&#xff0c;我们首先需要打开一个日…...

编程日记 2024/2/3 4:01:01

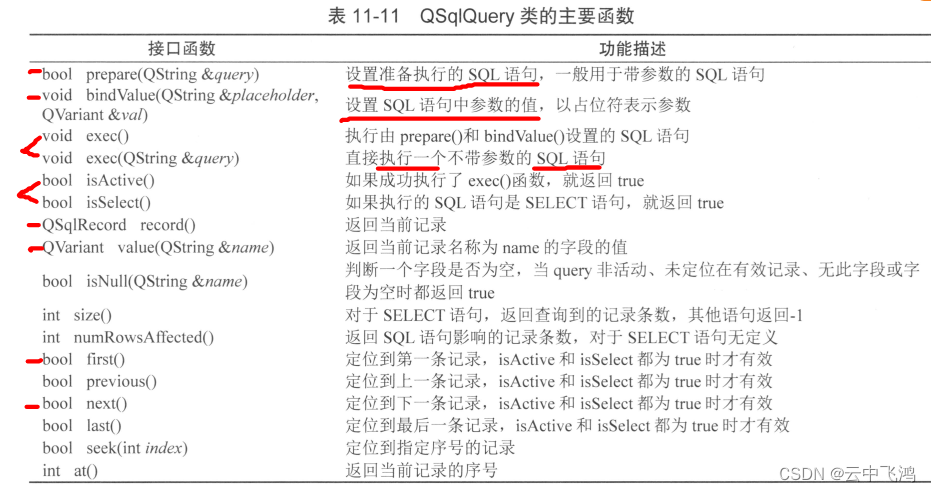
QT SQL

QT SQL模块提供数据库编程的支持&#xff0c;支持多种常见的数据库&#xff1a;MySQL\Oracle\MS SQL Server\SQLite等。SQL模块包含多个类&#xff0c;可以实现&#xff1a;数据库连接、SQL语句执行、数据获取与界面显示 等功能。数据 与 界面间用Model\View架构。 一、 二、Q…...

编程日记 2024/2/3 3:57:56

C++(20)：通过concept及nlohmann将数据转换为字符串

nlohmann可以自动兼容将C++的很多原生类型转换为json，甚至自定义类型也不需要太复杂的操作就可以转换为json，可以利用这一点将数据转换为string： #include <nlohmann/json.hpp> #include <string> #include <vector> #include <tuple> #include <…...

编程日记 2024/2/3 3:53:53

Transformer 自然语言处理（四）

原文&#xff1a;Natural Language Processing with Transformers 译者&#xff1a;飞龙 协议&#xff1a;CC BY-NC-SA 4.0 第十章&#xff1a;从头开始训练变换器 在本书的开头段落中&#xff0c;我们提到了一个名为 GitHub Copilot 的复杂应用&#xff0c;它使用类似 GPT 的…...

编程日记 2024/2/3 3:52:51

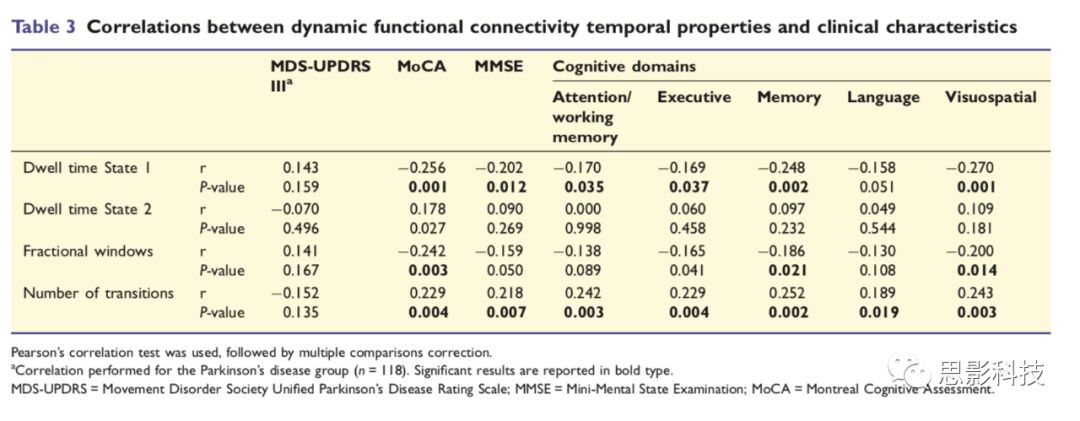
BRAIN ：帕金森病中与痴呆相关的动态功能连接改变

fMRI成像手段由于其在高空间分辨率的优势获得了疾病研究的青睐&#xff0c;越来越多的疾病研究使用fMRI手段来通过找到特异的神经标记物从而提升临床治疗的诊断效力以及准确率。但是&#xff0c;功能磁共振受到其时间分辨率相对较低这一缺点的影响&#xff0c;在对疾病时间特异…...

编程日记 2024/2/3 3:50:49

Java 8 Stream API 入门到实践详解

一、告别 for 循环&#xff01; 传统痛点&#xff1a; Java 8 之前&#xff0c;集合操作离不开冗长的 for 循环和匿名类。例如&#xff0c;过滤列表中的偶数&#xff1a; List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

编程新知 2026/1/12 10:41:22

Cesium1.95中高性能加载1500个点

一、基本方式&#xff1a; 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

编程新知 2025/12/17 2:10:10

五年级数学知识边界总结思考-下册

目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解&#xff1a;由来、作用与意义**一、知识点核心内容****二、知识点的由来&#xff1a;从生活实践到数学抽象****三、知识的作用&#xff1a;解决实际问题的工具****四、学习的意义&#xff1a;培养核心素养…...

编程新知 2025/10/7 4:57:55

C++ 基础特性深度解析

目录 引言 一、命名空间&#xff08;namespace&#xff09; C 中的命名空间​ 与 C 语言的对比​ 二、缺省参数​ C 中的缺省参数​ 与 C 语言的对比​ 三、引用&#xff08;reference&#xff09;​ C 中的引用​ 与 C 语言的对比​ 四、inline&#xff08;内联函数…...

编程新知 2026/1/15 4:25:16

Module Federation 和 Native Federation 的比较

前言 Module Federation 是 Webpack 5 引入的微前端架构方案&#xff0c;允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

编程新知 2026/1/31 13:48:37

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()

操作系统&#xff1a;ubuntu22.04 OpenCV版本&#xff1a;OpenCV4.9 IDE:Visual Studio Code 编程语言&#xff1a;C11 算法描述 在 GPU 上对图像执行 均值漂移滤波&#xff08;Mean Shift Filtering&#xff09;&#xff0c;用于图像分割或平滑处理。 该函数将输入图像中的…...

编程新知 2026/1/20 12:53:30

分布式增量爬虫实现方案

之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面&#xff0c;避免重复抓取&#xff0c;以节省资源和时间。 在分布式环境下&#xff0c;增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路&#xff1a;将增量判…...

编程新知 2026/2/6 1:18:56

均衡后的SNRSINR

本文主要摘自参考文献中的前两篇&#xff0c;相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程&#xff0c;其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt​ 根发送天线&#xff0c; n r n_r nr​ 根接收天线的 MIMO 系…...

编程新知 2026/1/30 4:47:24

rnn判断string中第一次出现a的下标

# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

编程新知 2025/9/24 16:25:00

SQL慢可能是触发了ring buffer

简介 最近在进行 postgresql 性能排查的时候，发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升，且低水位伴随在整个慢 SQL，一直是 buferIO 的等待事件，此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ，但…...

编程新知 2025/10/2 9:17:52